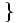Đại số 10/Chương I/§3. Các phép toán tập hợp
Mục lục
Lí thuyết[sửa]
Giao của hai tập hợp[sửa]
| Hoạt động 1 |
Cho
a) Liệt kê các phần tử của A và của B. b) Liệt kê các phần tử của tập hợp C là ước chung của 12 và 18. |
|
Tập
hợp
C
gồm
các
phần
tử
vừa
thuộc
A,
vừa
thuộc
B
được
gọi
là
giao
của
A
và
B.
|
|
Kí
hiệu
C
=
A
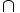 B
B
Từ
định
nghĩa
ta
có:
-
A
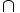 B
=
B
=
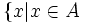 và
và
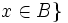
-
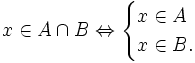
- (đọc là x thuộc A giao B khi và chỉ khi x thuộc A và thuộc B.)
-
A
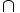 A
=
A,
A
A
=
A,
A
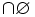 =
=
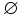 .
.
| VÍ DỤ 1 |
Cho
các
tập
hợp
Hãy
xác
định
các
tập
hợp:
A
Giải
|
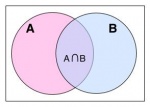
Hợp của hai tập hợp[sửa]
| Hoạt động 2 |
Giả
sử
A,
B
lần
lượt
là
tập
hợp
các
học
sinh
giỏi
Toán,
giỏi
Văn
của
lớp
10E.
Biết
(Các học sinh trong lớp không trùng tên nhau) Gọi C là tập hợp đội tuyển thi học sinh giỏi của lớp gồm các bạn giỏi Toán hoặc giỏi Văn. Hãy xác định tập hợp C. |
|
Tập
hợp
C
gồm
các
phần
tử
thuộc
A
hoặc
thuộc
B
được
gọi
là
hợp
của
A
và
B.
|
|
Kí
hiệu
C
=
A
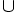 B
B
Từ định nghĩa ta có:
-
A
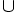 B
=
B
=
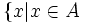 hoặc
hoặc
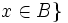
-
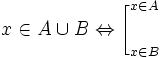
- (đọc là x thuộc A hợp B khi và chỉ khi x thuộc A hoặc thuộc B.)
-
A
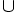 A
=
A,
A
A
=
A,
A
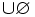 =
A
=
A
| VÍ DỤ 2 |
Cho
các
tập
hợp
Hãy
xác
định
các
tập
hợp:
A
Giải
|
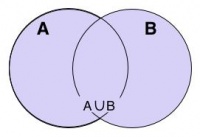
Hiệu và phần bù của hai tập hợp[sửa]
| Hoạt động 3 |
Giả
sử
tập
hợp
A
các
học
sinh
giỏi
của
lớp
10E
là
Tập hợp B gồm các học sinh của tổ 1 lớp 10E là
Xác định tập hợp C các học sinh giỏi của lớp 10E không thuộc tổ 1. |
|
Tập
hợp
C
gồm
các
phần
tử
thuộc
A
nhưng
không
thuộc
B
là
hiệu
của
A
và
B.
|
|
Kí hiệu C = A \ B
Từ định nghĩa ta có:
-
A
\
B
=
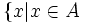 và
và
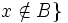
-
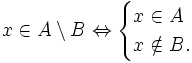
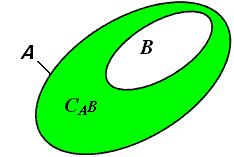
Trường hợp đặc biệt
|
Khi
B
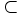 A
thì
A
\
B
gọi
là
phần
bù
của
B
trong
A
A
thì
A
\
B
gọi
là
phần
bù
của
B
trong
A |
|
Kí hiệu CAB
| VÍ DỤ 3 | |
BÀI TẬP[sửa]
1. Cho
-
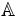 là
tập
hợp
các
chữ
cái
(không
dấu)
trong
câu:
"CO
CHI
THI
NEN"
là
tập
hợp
các
chữ
cái
(không
dấu)
trong
câu:
"CO
CHI
THI
NEN" -
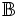 là
tập
hợp
các
chữ
cái
(không
dấu)
trong
câu:
"CO
CONG
MAI
SAT
CO
NGAY
NEN
KIM".
là
tập
hợp
các
chữ
cái
(không
dấu)
trong
câu:
"CO
CONG
MAI
SAT
CO
NGAY
NEN
KIM".
Hãy
xác
định
các
tập
hợp
sau:
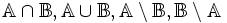
2.
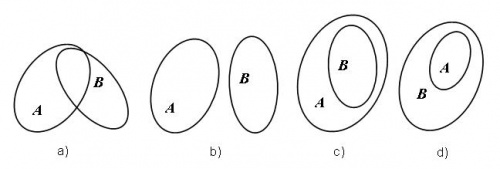
Vẽ
lại
và
gạch
chéo
các
tập
hợp
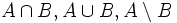 (Hình
9)
trong
các
trường
hợp
sau:
(Hình
9)
trong
các
trường
hợp
sau:
3.
Trong
số
45
học
sinh
của
lớp
10A
có
15
bạn
được
xếp
loại
học
lực
giỏi,
20
bạn
được
xếp
loại
hạnh
kiểm
tốt,
trong
đó
có
10
bạn
vừa
học
lực
giỏi,
vừa
có
hạnh
kiểm
tốt.
Hỏi
a) Lớp 10A có bao nhiêu bạn được khen thưởng, biết rằng muốn được khen thưởng bạn đó phải có học lực giỏi hoặc hạnh kiểm tốt?
b) Lớp 10A có bao nhiêu bạn chưa được xếp loại học lực giỏi và chưa có hạnh kiểm tốt?
4.
Bài
tập
nhóm
Học sinh 1: Cho một tập hợp A bất kì.
Học
sinh
2:
Xác
định
các
tập
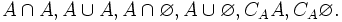
Liên kết ngoài[sửa]
- Bài giảng về Lý thuyết tập hợp ở Trường Đại học Cần Thơ
- Tập hợp trên Wikipedia
- Cơ bản về lý thuyết tập hợp
- Tập hợp trên MathWorld
- Notes on set theory



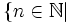 n
là
ước
của
12
n
là
ước
của
12