Đại số 10/Chương II/Ôn tập chương II
Bài tập tự luận[sửa]
1. Phát biểu quy ước về tập xác định của hàm số cho bởi công thức.
Từ
đó
cho
biết,
tập
xác
định
của
hai
hàm
số
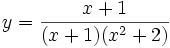 và
và
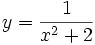 có
gì
khác
nhau?
có
gì
khác
nhau?
2. Thế nào là hàm số đồng biến (nghịch biến) trên khoảng (a;b)?
3. Thế nào là một hàm số chẵn? Thế nào là một hàm số lẻ?
4. Chỉ ra khoảng đồng biến, khoảng nghịch biến của hàm số y = ax + b, trong mỗi trường hợp a > 0 và a < 0.
5.
Chỉ
ra
khoảng
đồng
biến,
khoảng
nghịch
biến
của
hàm
số
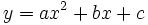 ,
trong
mỗi
trường
hợp
a
>
0
và
a
<
0.
,
trong
mỗi
trường
hợp
a
>
0
và
a
<
0.
6.
Xác
định
tọa
độ
của
đỉnh,
phương
trình
của
trục
đối
xứng
của
parabol
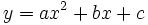 .
.
7.
Xác
định
tọa
độ
giao
điểm
của
parabol
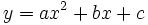 với
trục
tung.
Tìm
điều
kiện
để
parabol
này
cắt
trục
hoành
tại
hai
điểm
phân
biệt
và
viết
tọa
độ
của
các
giao
điểm
trong
trường
hợp
đó.
với
trục
tung.
Tìm
điều
kiện
để
parabol
này
cắt
trục
hoành
tại
hai
điểm
phân
biệt
và
viết
tọa
độ
của
các
giao
điểm
trong
trường
hợp
đó.
| 8. Tìm tập xác định của các hàm số | |
a)
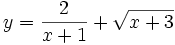
|
b)
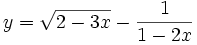
|
c)
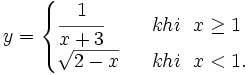
|
d) |
| 9. Xét chiều biến thiên và vẽ đồ thị của các hàm số | |
a)
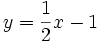
|
b)
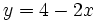
|
c)
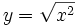
|
d)
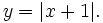
|
| 10. Lập bảng biến thiên và vẽ đồ thị của các hàm số | |
a)
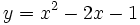
|
b)
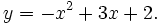
|
11. Xác định a, b biết đường thẳng y = ax + b đi qua hai điểm A(1;3), B(-1;5).
12.
Xác
định
a,
b,
c
biết
parabol
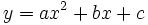
a) Đi qua ba điểm A(0;-1), B(1;-1), C(-1;1);
b) Có đỉnh I(1;4) và đi qua điểm D(3;0).
Bài tập trắc nghiệm[sửa]
Chọn phương án đúng trong các bài tập sau:
13.
Tập
xác
định
của
các
hàm
số
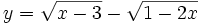 là
là |
|
(A)
![D=\left[{\frac {1}{2}};3\right]](https://tusach.thuvienkhoahoc.com/images/math/c/e/5/ce5561172d255f15e1337be5be03b399.png)
|
(B)
![D=\left[-\infty ;{\frac {1}{2}}\right]\cup [3;+\infty )](https://tusach.thuvienkhoahoc.com/images/math/9/4/a/94a2534d61d50c9fab1a40f2577493bf.png)
|
(C)
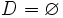
|
(D)
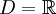
|
14.
Parabol
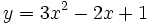 có
đỉnh
là
có
đỉnh
là |
|
(A)
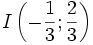
|
(B)
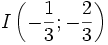
|
(C)
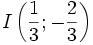
|
(D)
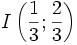
|
15.
Hàm
số
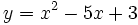
|
|
(A)
Đồng
biến
trên
khoảng
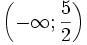
|
(B)
Đồng
biến
trên
khoảng
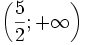
|
(C)
Nghịch
biến
trên
khoảng
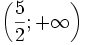
|
(D) Đồng biến trên khoảng (0;3). |


