Chủ đề nóng: Phương pháp kỷ luật tích cực - Cổ học tinh hoa - Những thói hư tật xấu của người Việt - Công lý: Việc đúng nên làm - Giáo án Điện tử - Sách giáo khoa - Học tiếng Anh - Bài giảng trực tuyến - Món ăn bài thuốc - Chăm sóc bà bầu - Môi trường - Tiết kiệm điện - Nhi khoa - Ung thư - Tác hại của thuốc lá - Các kỹ thuật dạy học tích cực
- Dạy học phát triển năng lực - Chương trình giáo dục phổ thông
Định lý Lagrange (số học)
Từ VLOS
Trong Lý thuyết số, 'định lý Lagrange khẳng định":
-
Nếu
p
là
số
nguyên
tố
và
f(x)
là
một
đa
thức
với
hệ
số
nguyên
thuộc
trường
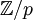 có
bậc
là
n
và
không
đồng
nhất
với
không
(nghĩa
là
có
ít
nhất
một
hệ
số
không
chia
hết
cho
p),
thì
phương
trình
có
bậc
là
n
và
không
đồng
nhất
với
không
(nghĩa
là
có
ít
nhất
một
hệ
số
không
chia
hết
cho
p),
thì
phương
trình
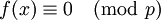 có
không
quá
n
nghiệm
trong
trường
có
không
quá
n
nghiệm
trong
trường
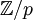 .
.
Nếu p không phải là số nguyên tố thì có thể có nhiều hơn n nghiệm.
Định lý được đặt theo tên của Joseph Lagrange.
Một chứng minh của định lý Lagrange[sửa]
Ta chứng minh quy nạp theo n.
Định lý hiển nhiên đúng với n=0.
Giả
sử
định
lý
đúng
với
n=k,
xét
đa
thức
không
đồng
nhất
với
không
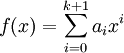 ,
deg(f)
=
k
+
1,
với
m
nghiệm.
,
deg(f)
=
k
+
1,
với
m
nghiệm.
Không
mất
tính
tổng
quát
giả
sử
m>0,
vậy
tồn
tại
r
sao
cho
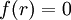 .
.
Khi
đó,
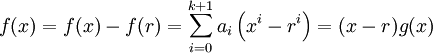 ,
với
g
là
đa
thức
có
bậc
nhỏ
thua
k+1.
Rõ
ràng,
,
với
g
là
đa
thức
có
bậc
nhỏ
thua
k+1.
Rõ
ràng,
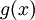 không
đồng
nhất
với
không,
do
đó
không
đồng
nhất
với
không,
do
đó
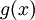 có
không
quá
k
nghiệm.
Kết
hợp
với
có
không
quá
k
nghiệm.
Kết
hợp
với
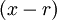 có
đúng
một
nghiệm,
suy
ra
có
đúng
một
nghiệm,
suy
ra
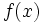 có
không
quá
k+1
nghiệm.
có
không
quá
k+1
nghiệm.
Suy ra điều phải chứng minh.


