Chương trình môn Toán/Nội dung giáo dục/Lớp 10

Đại số và một số yếu tố giải tích

Đại số

Tập hợp. Mệnh đề

Nội dung	Yêu cầu cần đạt
Mệnh đề toán học. Mệnh đề phủ định. Mệnh đề đảo. Mệnh đề tương đương. Điều kiện cần và đủ.	- Thiết lập và phát biểu được các mệnh đề toán học, bao gồm: mệnh đề phủ định; mệnh đề đảo; mệnh đề tương đương; mệnh đề có chứa kí hiệu V, 3; điều kiện cần, điều kiện đủ, điều kiện cần và đủ. - Xác định được tính đúng/sai của một mệnh đề toán học trong những trường hợp đơn giản.
Tập hợp. Các phép toán trên tập hợp	- Nhận biết được các khái niệm cơ bản về tập hợp (tập con, hai tập hợp bằng nhau, tập rỗng) và biết sử dụng các kí hiệu c, o, 0. - Thực hiện được phép toán trên các tập hợp (hợp, giao, hiệu của hai tập hợp, phần bù của một tập con) và biết dùng biểu đồ Ven để biểu diễn chúng trong những trường hợp cụ thể. - Giải quyết được một số vấn đề thực tiễn gắn với phép toán trên tập hợp (ví dụ: những bài toán liên quan đến đếm số phần tử của hợp các tập hợp,...).

Bất phương trình và hệ bất phương trình bậc nhất hai ẩn

Nội dung	Yêu cầu cần đạt
Bất phương trình, hệ bất phương trình bậc nhất hai ẩn và ứng dụng	- Nhận biết được bất phương trình và hệ bất phương trình bậc nhất hai ẩn. - Biểu diễn được miền nghiệm của bất phương trình và hệ bất phương trình bậc nhất hai ẩn trên mặt phẳng toạ độ. - Vận dụng được kiến thức về bất phương trình, hệ bất phương trình bậc nhất hai ẩn vào giải quyết bài toán thực tiễn (ví dụ: bài toán tìm cực trị của biểu thức F = ax + by trên một miền đa giác,...).

Hàm số và đồ thị

Nội dung	Yêu cầu cần đạt
Khái niệm cơ bản về hàm số và đồ thị	- Nhận biết được những mô hình thực tế (dạng bảng, biểu đồ, công thức) dẫn đến khái niệm hàm số. - Mô tả được các khái niệm cơ bản về hàm số: định nghĩa hàm số, tập xác định, tập giá trị, hàm số đồng biến, hàm số nghịch biến, đồ thị của hàm số. - Mô tả được các đặc trưng hình học của đồ thị hàm số đồng biến, hàm số nghịch biến. - Vận dụng được kiến thức của hàm số vào giải quyết bài toán thực tiễn (ví dụ: xây dựng hàm số bậc nhất trên những khoảng khác nhau để tính số tiền y (phải trả) theo số phút gọi x đối với một gói cước điện thoại,...).
Hàm số bậc hai, đồ thị hàm số bậc hai và ứng dụng	- Thiết lập được bảng giá trị của hàm số bậc hai. - Vẽ được Parabola (parabol) là đồ thị hàm số bậc hai. - Nhận biết được các tính chất cơ bản của Parabola như đỉnh, trục đối xứng. - Nhận biết và giải thích được các tính chất của hàm số bậc hai thông qua đồ thị. - Vận dụng được kiến thức về hàm số bậc hai và đồ thị vào giải quyết bài toán thực tiễn (ví dụ: xác định độ cao của cầu, cổng có hình dạng Parabola,...).
Dấu của tam thức bậc hai. Bất phương trình bậc hai một ẩn	- Giải thích được định lí về dấu của tam thức bậc hai từ việc quan sát đồ thị của hàm bậc hai. - Giải được bất phương trình bậc hai. - Vận dụng được bất phương trình bậc hai một ẩn vào giải quyết bài toán thực tiễn (ví dụ: xác định chiều cao tối đa để xe có thể qua hầm có hình dạng Parabola,...).
Phương trình quy về phương trình bậc hai	- Giải được phương trình chứa căn thức có dạng: ${\sqrt {ax^{2}+bx+c}}={\sqrt {dx^{2}+ex+f}}$ , ${\sqrt {ax^{2}+bx+c}}=dx+e$ .

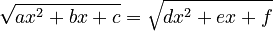Đại số tổ hợp

Nội dung	Yêu cầu cần đạt
Các quy tắc đếm (quy tắc cộng, quy tắc nhân, chỉnh hợp, hoán vị, tổ hợp) và ứng dụng trong thực tiễn	- Vận dụng được quy tắc cộng và quy tắc nhân trong một số tình huống đơn giản (ví dụ: đếm số khả năng xuất hiện mặt sấp/ngửa khi tung một số đồng xu,...). - Vận dụng được sơ đồ hình cây trong các bài toán đếm đơn giản các đối tượng trong Toán học, trong các môn học khác cũng như trong thực tiễn (ví dụ: đếm số hợp tử tạo thành trong Sinh học, hoặc đếm số trận đấu trong một giải thể thao,...). - Tính được số các hoán vị, chỉnh hợp, tổ hợp. - Tính được số các hoán vị, chỉnh hợp, tổ hợp bằng máy tính cầm tay.
Nhị thức Newton với số mũ không quá 5	Khai triển được nhị thức Newton (a + b)n với số mũ thấp (n = 4 hoặc n = 5) bằng cách vận dụng tổ hợp.

Thực hành phần mềm toán học

Thực hành trong phòng máy tính với phần mềm toán học (nếu nhà trường có điều kiện thực hiện)

Nội dung	Yêu cầu cần đạt
- Sử dụng phần mềm để hỗ trợ việc học các kiến thức đại số. - Thực hành sử dụng phần mềm để vẽ đồ thị của hàm số bậc hai; sử dụng đồ thị để tạo các hình ảnh hoa văn, hình khối.

Hình học và đo lường

Hình học phẳng

Hệ thức trong tam lượng giác. Vectơ

Nội dung	Yêu cầu cần đạt
Hệ thức lượng trong tam giác. Định lí côsin. Định lí sin. Công thức tính diện tích tam giác. Giải tam giác	- Nhận biết được giá trị lượng giác của một góc từ 0° đến 180°. - Tính được giá trị lượng giác (đúng hoặc gần đúng) của một góc từ 0° đến 180° bằng máy tính cầm tay. - Giải thích được hệ thức liên hệ giữa giá trị lượng giác của các góc phụ nhau, bù nhau. - Giải thích được các hệ thức lượng cơ bản trong tam giác: định lí côsin, định lí sin, công thức tính diện tích tam giác. - Mô tả được cách giải tam giác và vận dụng được vào việc giải một số bài toán có nội dung thực tiễn (ví dụ: xác định khoảng cách giữa hai địa điểm khi gặp vật cản, xác định chiều cao của vật khi không thể đo trực tiếp,...).
Vectơ, các phép toán (tổng và hiệu hai vectơ, tích của một số với vectơ, tích vô hướng của hai vectơ) và một số ứng dụng trong Vật lí	- Nhận biết được khái niệm vectơ, vectơ bằng nhau, vectơ-không. - Biểu thị được một số đại lượng trong thực tiễn bằng vectơ. - Thực hiện được các phép toán trên vectơ (tổng và hiệu hai vectơ, tích của một số với vectơ, tích vô hướng của hai vectơ) và mô tả được những tính chất hình học (ba điểm thẳng hàng, trung điểm của đoạn thẳng, trọng tâm của tam giác,...) bằng vectơ. - Sử dụng được vectơ và các phép toán trên vectơ để giải thích một số hiện tượng có liên quan đến Vật lí và Hoá học (ví dụ: những vấn đề liên quan đến lực, đến chuyển động,...). - Vận dụng được kiến thức về vectơ để giải một số bài toán hình học và một số bài toán liên quan đến thực tiễn (ví dụ: xác định lực tác dụng lên vật,...).

Phương pháp toạ độ trong mặt phẳng

Nội dung	Yêu cầu cần đạt
Toạ độ của vectơ đổi với một hệ trục toạ độ. Biểu thức toạ độ của các phép toán vectơ. Ứng dụng vào bài toán giải tam giác	- Nhận biết được toạ độ của vectơ đối với một hệ trục toạ độ. - Tìm được toạ độ của một vectơ, độ dài của một vectơ khi biết toạ độ hai đầu mút của nó. - Sử dụng được biểu thức toạ độ của các phép toán vectơ trong tính toán. - Vận dụng được phương pháp toạ độ vào bài toán giải tam giác. - Vận dụng được kiến thức về toạ độ của vectơ để giải một số bài toán liên quan đến thực tiễn (ví dụ: vị trí của vật trên mặt phẳng toạ độ,...).
Đường thẳng trong mặt phẳng toạ độ. Phương trình tổng quát và phương trình tham sổ của đường thẳng. Khoảng cách từ một điểm đến một đường thẳng	- Mô tả được phương trình tổng quát và phương trình tham số của đường thẳng trong mặt phẳng toạ độ. - Thiết lập được phương trình của đường thẳng trong mặt phẳng khi biết: một điểm và một vectơ pháp tuyến; biết một điểm và một vectơ chỉ phương; biết hai điểm. - Nhận biết được hai đường thẳng cắt nhau, song song, trùng nhau, vuông góc với nhau bằng phương pháp toạ độ. - Thiết lập được công thức tính góc giữa hai đường thẳng. - Tính được khoảng cách từ một điểm đến một đường thẳng bằng phương pháp toạ độ. - Giải thích được mối liên hệ giữa đồ thị hàm số bậc nhất và đường thẳng trong mặt phẳng toạ độ. - Vận dụng được kiến thức về phương trình đường thẳng để giải một số bài toán có liên quan đến thực tiễn.
Đường tròn trong mặt phẳng toạ độ và ứng dụng	- Thiết lập được phương trình đường tròn khi biết toạ độ tâm và bán kính; biết toạ độ ba điểm mà đường tròn đi qua; xác định được tâm và bán kính đường tròn khi biết phương trình của đường tròn. - Thiết lập được phương trình tiếp tuyến của đường tròn khi biết toạ độ của tiếp điểm. - Vận dụng được kiến thức về phương trình đường tròn để giải một số bài toán liên quan đến thực tiễn (ví dụ: bài toán về chuyển động tròn trong Vật lí,...).
Ba đường conic trong mặt phẳng toạ độ và ứng dụng	- Nhận biết được ba đường conic bằng hình học. - Nhận biết được phương trình chính tắc của ba đường conic trong mặt phẳng toạ độ. - Giải quyết được một số vấn đề thực tiễn gắn với ba đường conic (ví dụ: giải thích một số hiện tượng trong Quang học,...).

Thực hành phần mềm toán học

Thực hành trong phòng máy tính với phần mềm toán học (nếu nhà trường có điều kiện thực hiện)

Nội dung

Yêu cầu cần đạt

- Sử dụng phần mềm để hỗ trợ việc học các kiến thức hình học. - Thực hành sử dụng phần mềm để biểu thị điểm, vectơ, các phép toán vectơ trong hệ trục toạ độ Oxy. - Thực hành sử dụng phần mềm để vẽ đường thẳng, đường tròn, các đường conic trên mặt phẳng toạ độ; xem xét sự thay đổi hình dạng của các hình khi thay đổi các yếu tố trong phương trình xác định chúng. - Thực hành sử dụng phần mềm để thiết kế đồ hoạ liên quan đến đường tròn và các đường conic.

Thống kê và xác suất

Thống kê

Số gần đúng

Nội dung	Yêu cầu cần đạt
Số gần đúng. Sai số	- Hiểu được khái niệm số gần đúng, sai số tuyệt đối. - Xác định được số gần đúng của một số với độ chính xác cho trước. - Xác định được sai số tương đối của số gần đúng. - Xác định được số quy tròn của số gần đúng với độ chính xác cho trước. - Biết sử dụng máy tính cầm tay để tính toán với các số gần đúng.

Thu thập và tổ chức dữ liệu

Nội dung	Yêu cầu cần đạt
Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ	Phát hiện và lí giải được số liệu không chính xác dựa trên mối liên hệ toán học đơn giản giữa các số liệu đã được biểu diễn trong nhiều ví dụ.

Phân tích và xử lí dữ liệu

Nội dung	Yêu cầu cần đạt
Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu không ghép nhóm	- Tính được số đặc trưng đo xu thế trung tâm cho mẫu số liệu không ghép nhóm: số trung bình cộng (hay số trung bình), trung vị (median), tứ phân vị (quartiles), mốt (mode). - Giải thích được ý nghĩa và vai trò của các số đặc trưng nói trên của mẫu số liệu trong thực tiễn. - Chỉ ra được những kết luận nhờ ý nghĩa của số đặc trưng nói trên của mẫu số liệu trong trường hợp đơn giản.
Các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm	- Tính được số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm: khoảng biến thiên, khoảng tứ phân vị, phương sai, độ lệch chuẩn. - Giải thích được ý nghĩa và vai trò của các số đặc trưng nói trên của mẫu số liệu trong thực tiễn. - Chỉ ra được những kết luận nhờ ý nghĩa của số đặc trưng nói trên của mẫu số liệu trong trường hợp đơn giản. - Nhận biết được mối liên hệ giữa thống kê với những kiến thức của các môn học trong Chương trình lớp 10 và trong thực tiễn.

Xác suất

Khái niệm về xác suất

Nội dung	Yêu cầu cần đạt
Một số khái niệm về xác suất cổ điển	- Nhận biết được một số khái niệm về xác suất cổ điển: phép thử ngẫu nhiên; không gian mẫu; biến cố (biến cố là tập con của không gian mẫu); biến cố đối; định nghĩa cổ điển của xác suất; nguyên lí xác suất bé. - Mô tả được không gian mẫu, biến cố trong một số thí nghiệm đơn giản (ví dụ: tung đồng xu hai lần, tung đồng xu ba lần, tung xúc xắc hai lần).

Các quy tắc tính xác suất

Nội dung	Yêu cầu cần đạt
Thực hành tính toán xác suất trong những trường hợp đơn giản	- Tính được xác suất của biến cố trong một số bài toán đơn giản bằng phương pháp tổ hợp (trường hợp xác suất phân bố đều). - Tính được xác suất trong một số thí nghiệm lặp bằng cách sử dụng sơ đồ hình cây (ví dụ: tung xúc xắc hai lần, tính xác suất để tổng số chấm xuất hiện trong hai lần tung bằng 7).
Các quy tắc tính xác suất	- Mô tả được các tính chất cơ bản của xác suất. - Tính được xác suất của biến cố đối.

Thực hành phần mềm toán học

Thực hành trong phòng máy tính với phần mềm toán học (nếu nhà trường có điều kiện thực hiện)

Nội dung	Yêu cầu cần đạt
- Sử dụng phần mềm để hỗ trợ việc học các kiến thức thống kê và xác suất. - Thực hành sử dụng phần mềm để tính được số đặc trưng đo xu thế trung tâm và đo mức độ phân tán cho mẫu số liệu không ghép nhóm. - Thực hành sử dụng phần mềm để tính xác suất theo định nghĩa cổ điển.

Hoạt động thực hành và trải nghiệm

Nhà trường tổ chức cho học sinh một số hoạt động sau và có thể bổ sung các hoạt động khác tuỳ vào điều kiện cụ thể.

Nội dung

Yêu cầu cần đạt

Hoạt động 1: Thực hành ứng dụng các kiến thức toán học vào thực tiễn và các chủ đề liên môn, chẳng hạn: - Thực hành tổng hợp các hoạt động liên quan đến tính toán, đo lường, ước lượng và tạo lập hình, như: tính tiền khi đi taxi theo các khung giá: dưới 1km, từ 1 - 10km, từ 10 - 31km, trên 31km,...; đo đạc một vài yếu tố của vật thể mà chúng ta không thể dùng dụng cụ đo đạc để đo trực tiếp; tính chiều cao của công trình kiến trúc dạng Parabola (như cầu Nhật Tân, cầu Trường Tiền, cầu Mỹ Thuận,...); giải thích các hiện tượng, quy luật trong Vật lí; thực hành vẽ, cắt hình có dạng Ellipse (elip). - Thực hành mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ. Hoạt động 2: Tìm hiểu một số kiến thức về tài chính, như: - Hiểu sự khác biệt giữa tiết kiệm và đầu tư. - Thực hành thiết lập kế hoạch đầu tư cá nhân để đạt được tỉ lệ tăng trưởng như mong đợi. Hoạt động 3: Tổ chức các hoạt động ngoài giờ chính khoá như các câu lạc bộ toán học, dự án học tập, trò chơi học toán, cuộc thi về Toán, chẳng hạn: thi tìm hiểu lịch sử toán học, tổ chức sinh hoạt câu lạc bộ toán học theo các chủ đề (tìm hiểu các ứng dụng của hàm số bậc hai, vectơ trong thực tiễn,...). Hoạt động 4 (nếu nhà trường có điều kiện thực hiện): Tổ chức giao lưu học sinh giỏi trong trường và trường bạn, với các chuyên gia nhằm hiểu nhiều hơn về vai trò của Toán học trong thực tiễn và trong các ngành nghề.

Chuyên đề học tập

Xem chi tiết: Chương trình môn Toán/Nội dung giáo dục/Lớp 10/Chuyên đề học tập

Nguồn

• Chương trình tổng thể, Bộ Giáo dục và Đào tạo, tháng 12 năm 2018
• Biên tập: Thapsang.vn

Liên kết đến đây

• Chương trình môn Toán
• Chương trình môn Toán/Nội dung giáo dục