Chương trình môn Toán/Nội dung giáo dục/Lớp 12
Một số yếu tố giải tích[sửa]
Một số yếu tố giải tích[sửa]
Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số[sửa]
| Nội dung | Yêu cầu cần đạt |
|---|---|
| Tính đơn điệu của hàm số |
-
Nhận
biết
được
tính
đồng
biến,
nghịch
biến
của
một
hàm
số
trên
một
khoảng
dựa
vào
dấu
của
đạo
hàm
cấp
một
của
nó.
- Thể hiện được tính đồng biến, nghịch biến của hàm số trong bảng biến thiên. - Nhận biết được tính đơn điệu, điểm cực trị, giá trị cực trị của hàm số thông qua bảng biến thiên hoặc thông qua hình ảnh hình học của đồ thị hàm số. |
| Giá trị lớn nhất, giá trị nhỏ nhất của hàm số |
-
Nhận
biết
được
giá
trị
lớn
nhất,
giá
trị
nhỏ
nhất
của
hàm
số
trên
một
tập
xác
định
cho
trước.
- Xác định được giá trị lớn nhất, giá trị nhỏ nhất của hàm số bằng đạo hàm trong những trường hợp đơn giản. |
| Khảo sát và vẽ đồ thị của hàm số |
-
Nhận
biết
được
hình
ảnh
hình
học
của
đường
tiệm
cận
ngang,
đường
tiệm
cận
đứng,
đường
tiệm
cận
xiên
của
đồ
thị
hàm
số.
- Mô tả được sơ đồ tổng quát để khảo sát hàm số (tìm tập xác định, xét chiều biến thiên, tìm cực trị, tìm tiệm cận, lập bảng biến thiên, vẽ đồ thị). - Khảo sát được tập xác định, chiều biến thiên, cực trị, tiệm cận, bảng biến thiên và vẽ đồ thị của các hàm số:
- Nhận biết được tính đối xứng (trục đối xứng, tâm đối xứng) của đồ thị các hàm số trên. |
| Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn | Vận dụng được đạo hàm và khảo sát hàm số để giải quyết một số vấn đề liên quan đến thực tiễn. |
Nguyên hàm. Tích phân[sửa]
| Nội dung | Yêu cầu cần đạt |
|---|---|
| Nguyên hàm. Bảng nguyên hàm của một số hàm số sơ cấp |
-
Nhận
biết
được
khái
niệm
nguyên
hàm
của
một
hàm
số.
- Giải thích được tính chất cơ bản của nguyên hàm.
-
Xác
định
được
nguyên
hàm
của
một
số
hàm
số
sơ
cấp
như:
- Tính được nguyên hàm trong những trường hợp đơn giản. |
| Tích phân. Ứng dụng hình học của tích phân |
-
Nhận
biết
được
định
nghĩa
và
các
tính
chất
của
tích
phân.
- Tính được tích phân trong những trường hợp đơn giản. - Sử dụng được tích phân để tính diện tích của một số hình phẳng, thể tích của một số hình khối. - Vận dụng được tích phân để giải một số bài toán có liên quan đến thực tiễn. |
Thực hành phần mềm toán học[sửa]
Thực hành trong phòng máy tính với phần mềm toán học (nếu nhà trường có điều kiện thực hiện)
| Nội dung | Yêu cầu cần đạt |
|---|---|
|
-
Sử
dụng
phần
mềm
để
hỗ
trợ
việc
học
các
kiến
thức
đại
số
và
giải
tích.
- Thực hành sử dụng phần mềm để vẽ các đồ thị; minh hoạ sự tương giao của các đồ thị; thực hiện các phép biến đổi đồ thị; tạo hoa văn, hình khối. - Thực hành sử dụng phần mềm để tạo mô hình khối tròn xoay trong một số bài toán ứng dụng tích phân xác định. |
|
Hình học và đo lường[sửa]
Hình học không gian[sửa]
Phương pháp toạ độ trong không gian[sửa]
| Nội dung | Yêu cầu cần đạt |
|---|---|
| Toạ độ của vectơ đối với một hệ trục toạ độ. Biểu thức toạ độ của các phép toán vectơ |
-
Nhận
biết
được
vectơ
và
các
phép
toán
vectơ
trong
không
gian
(tổng
và
hiệu
của
hai
vectơ,
tích
của
một
số
với
một
vectơ,
tích
vô
hướng
của
hai
vectơ).
- Nhận biết được toạ độ của một vectơ đối với hệ trục toạ độ. - Xác định được độ dài của một vectơ khi biết toạ độ hai đầu mút của nó và biểu thức toạ độ của các phép toán vectơ. - Xác định được biểu thức toạ độ của các phép toán vectơ. - Vận dụng được toạ độ của vectơ để giải một số bài toán có liên quan đến thực tiễn. |
| Phương trình mặt phẳng |
-
Nhận
biết
được
phương
trình
tổng
quát
của
mặt
phẳng.
- Thiết lập được phương trình tổng quát của mặt phẳng trong hệ trục toạ độ Oxyz theo một trong ba cách cơ bản: qua một điểm và biết vectơ pháp tuyến; qua một điểm và biết cặp vectơ chỉ phương (suy ra vectơ pháp tuyến nhờ vào việc tìm vectơ vuông góc với cặp vectơ chỉ phương); qua ba điểm không thẳng hàng. - Thiết lập được điều kiện để hai mặt phẳng song song, vuông góc với nhau. - Tính được khoảng cách từ một điểm đến một mặt phẳng bằng phương pháp toạ độ. - Vận dụng được kiến thức về phương trình mặt phẳng để giải một số bài toán liên quan đến thực tiễn. |
| Phương trình đường thẳng trong không gian |
-
Nhận
biết
được
phương
trình
chính
tắc,
phương
trình
tham
số,
vectơ
chỉ
phương
của
đường
thẳng
trong
không
gian.
- Thiết lập được phương trình của đường thẳng trong hệ trục toạ độ theo một trong hai cách cơ bản: qua một điểm và biết một vectơ chỉ phương, qua hai điểm. - Xác định được điều kiện để hai đường thẳng chéo nhau, cắt nhau, song song hoặc vuông góc với nhau. - Thiết lập được công thức tính góc giữa hai đường thẳng, giữa đường thẳng và mặt phẳng, giữa hai mặt phẳng. - Vận dụng được kiến thức về phương trình đường thẳng trong không gian để giải một số bài toán liên quan đến thực tiễn. |
| Phương trình mặt cầu |
-
Nhận
biết
được
phương
trình
mặt
cầu.
- Xác định được tâm, bán kính của mặt cầu khi biết phương trình của nó. - Thiết lập được phương trình của mặt cầu khi biết tâm và bán kính. - Vận dụng được kiến thức về phương trình mặt cầu để giải một số bài toán liên quan đến thực tiễn. |
Thực hành phần mềm toán học[sửa]
Thực hành trong phòng máy tính với phần mềm toán học (nếu nhà trường có điều kiện thực hiện)
| Nội dung | Yêu cầu cần đạt |
|---|---|
|
-
Sử
dụng
phần
mềm
để
hỗ
trợ
việc
học
các
kiến
thức
hình
học.
- Thực hành sử dụng phần mềm để biểu thị điểm, vectơ, các phép toán vectơ trong hệ trục toạ độ Oxyz. - Thực hành sử dụng phần mềm để vẽ đường thẳng, mặt phẳng, mặt cầu trong hệ trục toạ độ Oxyz; xem xét sự thay đổi hình dạng khi thay đổi các yếu tố trong phương trình của chúng. |
|
Thống kê và xác suất[sửa]
Thống kê[sửa]
Phân tích và xử lí dữ liệu[sửa]
| Nội dung | Yêu cầu cần đạt |
|---|---|
| Các số đặc trưng của mẫu số liệu ghép nhóm |
-
Tính
được
các
số
đặc
trưng
đo
mức
độ
phân
tán
cho
mẫu
số
liệu
ghép
nhóm:
khoảng
biến
thiên,
khoảng
tứ
phân
vị,
phương
sai,
độ
lệch
chuẩn.
- Giải thích được ý nghĩa và vai trò của các số đặc trưng nói trên của mẫu số liệu trong thực tiễn. - Chỉ ra được những kết luận nhờ ý nghĩa của các số đặc trưng nói trên của mẫu số liệu trong trường hợp đơn giản. - Nhận biết được mối liên hệ giữa thống kê với những kiến thức của các môn học khác trong Chương trình lớp 12 và trong thực tiễn. |
Xác suất[sửa]
Khái niệm về xác suất có điều kiện[sửa]
| Nội dung | Yêu cầu cần đạt |
|---|---|
| Xác suất có điều kiện |
-
Nhận
biết
được
khái
niệm
về
xác
suất
có
điều
kiện.
- Giải thích được ý nghĩa của xác suất có điều kiện trong những tình huống thực tiễn quen thuộc. |
Các quy tắc tính xác suất[sửa]
| Nội dung | Yêu cầu cần đạt |
|---|---|
| Các quy tắc tính xác suất |
-
Mô
tả
được
công
thức
xác
suất
toàn
phần,
công
thức
Bayes
thông
qua
bảng
dữ
liệu
thống
kê
2x2
và
sơ
đồ
hình
cây.
- Sử dụng được công thức Bayes để tính xác suất có điều kiện và vận dụng vào một số bài toán thực tiễn. - Sử dụng được sơ đồ hình cây để tính xác suất có điều kiện trong một số bài toán thực tiễn liên quan tới thống kê. |
Thực hành phần mềm toán học[sửa]
Thực hành trong phòng máy tính với phần mềm toán học (nếu nhà trường có điều kiện thực hiện)
| Nội dung | Yêu cầu cần đạt |
|---|---|
|
-
Sử
dụng
phần
mềm
để
hỗ
trợ
việc
học
các
kiến
thức
thống
kê
và
xác
suất.
- Thực hành sử dụng phần mềm để tính phân bố nhị thức, tính toán thống kê. |
|
Hoạt động thực hành và trải nghiệm[sửa]
Nhà trường tổ chức cho học sinh một số hoạt động sau và có thể bổ sung các hoạt động khác tuỳ vào điều kiện cụ thể.
| Nội dung | Yêu cầu cần đạt |
|---|---|
|
Hoạt
động
1:
Thực
hành
ứng
dụng
các
kiến
thức
toán
học
vào
thực
tiễn
và
các
chủ
đề
liên
môn,
chẳng
hạn:
- Thực hành tổng hợp các hoạt động liên quan đến tính toán, đo lường, ước lượng và tạo lập hình. - Vận dụng kiến thức về phương pháp toạ độ trong hình học không gian để tìm hiểu hệ thống GPS, tìm hiểu về đồ hoạ, vẽ kĩ thuật và thiết kế trong Công nghệ. - Vận dụng kiến thức về đạo hàm để giải thích các quy luật của Vật lí (quy luật âm học, quang học), Hoá học và giải quyết bài toán tối ưu về kinh tế, thời gian, quãng đường,... Hoạt động 2: Vận dụng các kiến thức toán học vào một số vấn đề liên quan đến tài chính. Hoạt động 3: Tổ chức các hoạt động ngoài giờ chính khoá: câu lạc bộ toán học; cuộc thi về Toán; dự án học tập; ra báo tường (hoặc nội san) về Toán, chẳng hạn: câu lạc bộ về ứng dụng toán học trong khoa học máy tính và công nghệ thông tin. Hoạt động 4 (nếu nhà trường có điều kiện thực hiện): Tổ chức giao lưu học sinh giỏi Toán trong trường và trường bạn, giao lưu với các chuyên gia nhằm hiểu vai trò của Toán học trong thực tiễn và trong các ngành nghề,... |
|
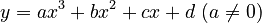 ;
;
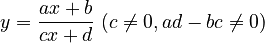 ;
;
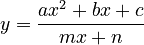 (a
≠
0,
m
≠
0
và
đa
thức
tử
không
chia
hết
cho
đa
thức
mẫu).
(a
≠
0,
m
≠
0
và
đa
thức
tử
không
chia
hết
cho
đa
thức
mẫu).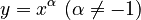 ;
;
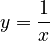 ;
;
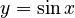 ;
;
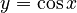 ;
;
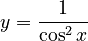 ;
;
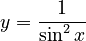 ;
;
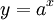 ;
;
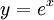 .
.

