Giải tích số

Tập tin:Ybc7289-bw.jpg

Bản ghi Babylon YBC 7289 (khoảng 1800–1600 TCN) với cách tính căn bậc hai của 2 bằng bốn phép cộng phân số, liên quan đến hệ lục thập phân (cơ số 60). 1 + 24/60 + 51/60² + 10/60³ = 1.41421296... Ảnh của Bill Casselman.

Giải tích số là ngành nghiên cứu về thuật toán sử dụng các số xấp xỉ đối với hàm liên tục (phân biệt với toán học rời rạc).

Một trong những bản ghi chép toán học sớm nhất về giải tích số là một bản ghi Babylon YBC 7289, trong đó nêu một phép tính xấp xỉ 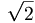${\sqrt {2}}$ , độ dài đường chéo của hình vuông đơn vị.

Phương pháp trực tiếp và phương pháp lặp

Phương pháp trực tiếp và phương pháp lặp Xét bài toán 3x3+4=28 tìm x. Phương pháp trực tiếp 3x3 + 4 = 28. Trừ 4 3x3 = 24. Chia cho 3 x3 = 8. Lấy căn bậc ba x = 2. Đối với phương pháp lặp, đặt f(x) = 3x3 - 24. Lấy a = 0, b = 3, f(a) = -24, f(b) = 57. Phương pháp lặp a b trung gian f(trung gian) 0 3 1.5 -13.875 1.5 3 2.25 10.17... 1.5 2.25 1.875 -4.22... 1.875 2.25 2.0625 2.32... Theo bảng này, ta thấy nghiệm của phương trình nằm giữa 1.875 và 2.0625. Ta có thể lấy nghiệm là bất cứ giá trị nào trong đoạn này với sai số nhỏ hơn 0.2.

Rời rạc hóa

Đôi khi bài toán liên tục được thay thế bằng bài toán rời rạc. Lời giải của nó được xấp xỉ cho bài toán liên tục. Người ta gọi là rời rạc hóa.^{[cần dẫn nguồn]}

Tham khảo

• Gilat, Amos (2004). MATLAB: An Introduction with Applications (ấn bản 2nd edition). John Wiley & Sons. ISBN 0-471-69420-7.
• Hildebrand, F. B. (1974). Introduction to Numerical Analysis (ấn bản 2nd edition). McGraw-Hill. ISBN 0-070-28761-9.
• Leader, Jeffery J. (2004). Numerical Analysis and Scientific Computation. Addison Wesley. ISBN 0-201-73499-0.
• Trefethen, Lloyd N. (2006). "Numerical analysis", 20 pages. In: Timothy Gowers and June Barrow-Green (editors), Princeton Companion of Mathematics, Princeton University Press.

Liên kết ngoài

• Numerische Mathematik, volumes 1-66, Springer, 1959-1994 (searchable; pages are images). Bản mẫu:En icon Bản mẫu:De icon
• Numerische Mathematik at SpringerLink, volumes 1-112, Springer, 1959–2009
• SIAM Journal on Numerical Analysis, volumes 1-47, SIAM, 1964–2009
• Lists of free software for scientific computing and numerical analysis Bản mẫu:En icon Bản mẫu:Fr icon
• Numerical methods for Fortran programmers
• Java Number Cruncher features free, downloadable code samples that graphically illustrate common numerical algorithms
• Excel Implementations
• Several Numerical Mathematical Utilities (in Javascript)
• Numerical Recipes, William H. Press (free, downloadable previous editions)
• First Steps in Numerical Analysis, R.J.Hosking, S.Joe, D.C.Joyce, and J.C.Turner
• Numerical Analysis for Engineering, D. W. Harder
• CSEP (Computational Science Education Project), U.S. Department of Energy
• Numerical Methods, Stuart Dalziel University of Cambridge
• Lectures on Numerical Analysis, Dennis Deturck and Herbert S. Wilf University of Pennsylvania
• Numerical methods, John D. Fenton University of Karlsruhe
• Numerical Methods for Science, Technology, Engineering and Mathematics, Autar Kaw University of South Florida
• Numerical Analysis Project, John H. Mathews California State University, Fullerton
• Numerical Methods - Online Course, Aaron Naiman Jerusalem College of Technology
• Numerical Methods for Physicists, Anthony O’Hare Oxford University
• Lectures in Numerical Analysis, R. Radok Mahidol University
• Introduction to Numerical Analysis for Engineering, Henrik Schmidt Massachusetts Institute of Technology

Bản mẫu:Toán Bản mẫu:Khoa học Máy tính

Liên kết đến đây

• Giải tích toán học
• Toán học
• Khoa học máy tính