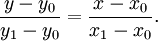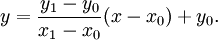Giải thuật vẽ đoạn thẳng Bresenham
Giải thuật vẽ đoạn thẳng Bresenham (tiếng Anh: Bresenham's line algorithm) là giải thuật xác định các điểm raster hai chiều cần vẽ để nhận được xấp xỉ gần đúng của đoạn thẳng có hai đầu mút là 2 điểm cho trước. Đây là một trong những thuật toán cổ nhất trong đồ họa máy tính. Thuật toán này được Jack E. Bresenham thiết kế vào năm 1962 tại công ty IBM. Thuật toán được sử dụng rộng rãi, đặc biệt để vẽ đoạn thẳng trên màn hình máy tính. Nó chỉ sử dụng các lệnh cộng trừ số học và lệnh trên pixel, có chi phí rẻ và phù hợp với kiến trúc sơ khai của máy tính. Đây là một trong những giải thuật đồ họa máy tính phát triển sớm nhất. Sự mở rộng của giải thuật này là giải thuật vẽ các đường cong bậc 2.
Mặc dù các giải thuật khác như giải thuật Xiaolin_Wu cũng thường được sử dụng trong đồ họa máy tính hiện đại vì có tính năng khử răng cưa (tiếng Anh: antialiasing), nhưng tốc độ và sự đơn giản của giải thuật Bresenham cho thấy nó vẫn còn quan trọng. Giải thuật được tích hợp lên phần cứng như plotter hay lên chip đồ họa của những card đồ họa hiện đại. Nó cũng được tìm thấy trong nhiều phần mềm thư viện đồ họa. Bởi vì giải thuật cực kì đơn giản, nên nó thường được thực hiện cả trong firmware lẫn trong phần cứng của card đồ họa hiện đại.
Ngày nay nhãn hiệu "Bresenham" được dùng cho cả họ giải thuật biến đổi hoặc mở rộng giải thuật Bresenham nguyên thủy. Xin hãy xem thêm phần tham khảo bên dưới.
Mục lục
Giải thuật Bresenham[sửa]
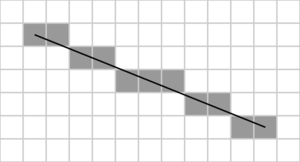
Đoạn thẳng được vẽ giữa hai điểm (x0,y0) và (x1,y1), trong đó x0, x1 là các tọa độ cột, còn y0,y1 là các tọa độ hàng, số thứ tự của chúng tăng dần từ trái sang phải và từ trên xuống dưới.
Giải
thuật
ban
đầu
sẽ
được
trình
bày
chỉ
cho
trường
hợp
góc
phần
tám,
trong
đó
đoạn
thẳng
đi
xuống
và
sang
phải
(x0≤x1
và
y0≤y1),
và
hình
chiếu
ngang
của
nó
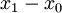 dài
hơn
hình
chiếu
đứng
dài
hơn
hình
chiếu
đứng
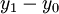 (đường
thẳng
có
hệ
số
góc
nhỏ
hơn
1
và
lớn
hơn
0),
hay
góc
nghiêng
của
đường
thẳng
so
với
phương
ngang
nhỏ
hơn
45
độ.
Trong
góc
phần
tám
này,
với
mỗi
cột
x
nằm
giữa
(đường
thẳng
có
hệ
số
góc
nhỏ
hơn
1
và
lớn
hơn
0),
hay
góc
nghiêng
của
đường
thẳng
so
với
phương
ngang
nhỏ
hơn
45
độ.
Trong
góc
phần
tám
này,
với
mỗi
cột
x
nằm
giữa
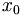 và
và
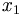 ,
có
chính
xác
một
hàng
y
(được
tính
bởi
giải
thuật)
chứa
một
pixel
của
đường
thẳng,
trong
khi
đó
mỗi
hàng
nằm
giữa
,
có
chính
xác
một
hàng
y
(được
tính
bởi
giải
thuật)
chứa
một
pixel
của
đường
thẳng,
trong
khi
đó
mỗi
hàng
nằm
giữa
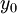 và
và
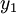 có
thể
chứa
nhiều
rasterized
pixels.
có
thể
chứa
nhiều
rasterized
pixels.
Phương trình tổng quát của đường thẳng đi qua hai điểm:
Vì chúng ta biết cột = x, nên hàng của pixel - y được tính bằng cách làm tròn giá trị sau đây đến số nguyên gần nhất:
Tuy
nhiên,
tính
giá
trị
chính
xác
của
biểu
thức
này
là
không
cần
thiết,
cần
chú
ý
rằng
y
tăng
từ
y0
và
sau
mỗi
bước
chúng
ta
thêm
vào
x
một
đơn
vị
và
thêm
vào
y
giá
trị
của
hệ
số
góc
s
=
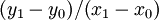 .
Hệ
số
góc
s
chỉ
phụ
thuộc
vào
các
tọa
độ
điểm
mút
nên
có
thể
tính
trước
được.
Hơn
nữa,
ở
mỗi
bước
chúng
ta
chọn
làm
một
trong
hai
việc:
hoặc
là
giữ
nguyên
y,
hoặc
là
tăng
y
lên
1
đơn
vị.
.
Hệ
số
góc
s
chỉ
phụ
thuộc
vào
các
tọa
độ
điểm
mút
nên
có
thể
tính
trước
được.
Hơn
nữa,
ở
mỗi
bước
chúng
ta
chọn
làm
một
trong
hai
việc:
hoặc
là
giữ
nguyên
y,
hoặc
là
tăng
y
lên
1
đơn
vị.
Có thể giải quyết việc lựa chọn này bằng cách lần theo giá trị sai số. Giá trị sai số là khoảng cách giữa giá trị y hiện tại và giá trị y chính xác đối với x hiện tại. Mỗi lần khi chúng ta tăng x, chúng ta sẽ tăng thêm vào giá trị sai số một đại lượng s, s là hệ số góc nói ở trên. Nếu sai số vượt quá 0.5, rasterization y sẽ được tăng thêm 1 (đường thẳng tiếp tục trên hàng raster bên dưới tiếp theo) và sai số giảm đi 1.0.
Trong
mẫu
mã
giả
dưới
đây
plot(x,y)
vẽ
một
điểm
và
abs
trả
về
giá
trị
tuyệt
đối:
function line(x0, x1, y0, y1) int deltax := x1 - x0 int deltay := y1 - y0 real error := 0 real deltaerr := deltay / deltax // Giả định deltax != 0 (đường thẳng không thẳng đứng), // chú ý: phép chia này cần được thực hiện sao cho nó có thể giữ lại phần thập phân int y := y0 for x from x0 to x1 plot(x,y) error := error + deltaerr if abs(error) ≥ 0.5 then y := y + 1 error := error - 1.0
Tổng quát hóa[sửa]
Phiên
bản
ở
trên
chỉ
điều
khiển
đường
đi
xuống
về
bên
phải.
Tất
nhiên
mong
muốn
của
chúng
ta
là
có
thể
vẽ
được
tất
cả
các
đường.
Trường
hợp
đầu
tiên
cho
phép
chúng
ta
vẽ
các
đường
có
hệ
số
gốc
dốc
xuống
nhưng
có
đầu
ở
hướng
đối
diện.
Việc
này
rất
đơn
giản
nhờ
việc
tráo
các
điểm
khởi
tạo
nếu
x0
>
x1.
Việc
khó
hơn
là
cần
xác
định
làm
cách
nào
để
có
thể
vẽ
các
đường
đi
lên.
Để
làm
việc
này,
chúng
ta
sẽ
kiểm
tra
y0
≥
y1
có
đúng
không;
nếu
đúng
vậy,
chúng
ta
sẽ
thay
đổi
bước
y
bởi
-1
thay
vì
1.
Sau
cùng,
chúng
ta
vẫn
cần
phải
tổng
quát
hóa
giải
thuật
để
có
thể
vẽ
các
đường
trong
mọi
hướng.
Cho
đến
lúc
này,
chúng
ta
chỉ
có
thể
vẽ
các
đường
có
hệ
số
góc
nhỏ
hơn
1.
Để
có
thể
vẽ
các
đường
có
hệ
số
góc
lớn
hơn
(đường
dốc
hơn),
chúng
ta
tận
dụng
thực
tế
là
một
đường
dốc
có
thể
được
phản
xạ
qua
đường
thẳng
y=x
để
nhận
được
một
đường
có
hệ
số
góc
(độ
dốc)
nhỏ.
Hiệu
ứng
này
là
tráo
đổi
các
biến
x
và
y
khắp
nơi,
bao
gồm
luôn
việc
tráo
đổi
các
tham
số
để
plot
(vẽ,
chấm
điểm).
Mã
chương
trình
có
thể
trông
như
sau:
function line(x0, x1, y0, y1)
boolean steep := abs(y1 - y0) > abs(x1 - x0)
if steep then
swap(x0, y0)
swap(x1, y1)
if x0 > x1 then
swap(x0, x1)
swap(y0, y1)
int deltax := x1 - x0
int deltay := abs(y1 - y0)
real error := 0
real deltaerr := deltay / deltax
int ystep
int y := y0
if y0 < y1 then ystep := 1 else ystep := -1
for x from x0 to x1
if steep then plot(y,x) else plot(x,y)
error := error + deltaerr
if error ≥ 0.5 then
y := y + ystep
error := error - 1.0
Bây giờ, hàm điều khiển tất cả các đường và thực hiện giải thuật Bresenham trọn vẹn.
Tối ưu hóa[sửa]
Phương
pháp
này
có
vấn
đề
ở
chỗ
các
máy
tính
hoạt
động
tương
đối
chậm
trên
các
số
thập
phân
như
error
và
deltaerr;
hơn
nữa,
các
sai
số
có
thể
được
tích
lũy
qua
nhiều
phép
cộng
số
thực
(floating-point
addition).
Làm
việc
với
số
nguyên
vừa
nhanh
hơn
vừa
chính
xác
hơn.
Thủ
thuật
chúng
ta
sử
dụng
đó
là
nhân
tất
cả
các
số
thập
phân
ở
trên
với
deltax,
việc
này
cho
phép
chúng
ta
biểu
diễn
chúng
như
các
số
nguyên.
Vấn
đề
duy
nhất
còn
lại
đó
là
hằng
số
0.5—
để
giải
quyết
việc
này,
chúng
ta
thay
đổi
việc
khởi
tạo
biến
error,
và
hoán
đổi
nó
cho
một
tối
ưu
hóa
bổ
sung.
Chương
trình
mới
sẽ
như
sau:
function line(x0, x1, y0, y1)
boolean steep := abs(y1 - y0) > abs(x1 - x0)
if steep then
swap(x0, y0)
swap(x1, y1)
if x0 > x1 then
swap(x0, x1)
swap(y0, y1)
int deltax := x1 - x0
int deltay := abs(y1 - y0)
int error := deltax / 2
int ystep
int y := y0
if y0 < y1 then ystep := 1 else ystep := -1
for x from x0 to x1
if steep then plot(y,x) else plot(x,y)
error := error - deltay
if error < 0 then
y := y + ystep
error := error + deltax
Lịch sử[sửa]
Thuật toán được phát triển bởi Jack E. Bresenham vào năm 1962 tại công ty IBM. Vào năm 2001 Bresenham đã viết:[1]
| “ | Lúc đó, tôi đang làm việc trong lab tính toán tại Lab phát triển San Jose của IBM. Một Calcomp plotter đã được gắn với IBM 1401 qua console typewriter 1407. Giải thuật được ứng dụng trong sản xuất vào mùa hè năm 1962, có thể sớm hay muộn hơn một tháng. Các chương trình trong những ngày đó có thể được trao đổi tự do giữa các công ty nên Calcomp (Jim Newland và Calvin Hefte) đã copy. Khi tôi trở về Stanford vào mùa thu năm 1962, tôi đã để lại một bản copy trong thư viện trung tâm Stanford comp. | ” |
Bản miêu tả của routine (đoạn chương trình) vẽ đường được chấp nhận trình bày ở hội nghị quốc gia ACM năm 1963 ở Denver, Colorado. Lúc đó đã một năm trôi qua không có các thủ tục tố tụng nào được công bố, chỉ có chương trình nghị sự của các diễn giả và các đề tài trong một ấn phẩm của Truyền thông ACM (Communications of the ACM). Sau khi tôi trình bày xong, một người từ tạp chí IBM Systems Journal đã hỏi tôi có thể xuất bản bài báo đó được không. Tôi đã sung sướng đồng ý, và họ đã in nó vào năm 1965.
Giải thuật Bresenham sau đó được biến đổi để tạo ra các đường tròn, đôi khi nó được biết đến với tên gọi là "giải thuật đường tròn Bresenham" hay giải thuật điểm giữa đường tròn (tiếng Anh: midpoint circle algorithm).
Các giải thuật tương tự[sửa]
Giải thuật Bresenham có thể được hiểu là biến đổi nhỏ của thuật toán DDA (dùng 0.5 là ngưỡng sai số thay cho 0, phép raster hóa đa giác không chồng chập cần 0).
Nguyên tắc sử dụng sai số tăng thay cho phép tính chia có các ứng dụng khác trong đồ họa. Có thể dùng kĩ thuật này để tính các tọa độ U,V trong quá trình quét raster của kết cấu đa giác ánh xạ (texture mapped polygon). Các lõi phần mềm dựng hình heightmap voxel thấy trong các trò chơi máy tính cũng đã sử dụng nguyên tắc này.
Bresenham cũng đã công bố giải thuật tính toán Run-Slice (trái ngược với Run-Length).
Một mở rộng của giải thuật Bresenham để điều khiển các đường có bề dày được tạo ra bởi Alan Murphy ở IBM.
Xem thêm[sửa]
- Digital Differential Analyzer (graphics algorithm) là phương pháp chung đơn giản để raster hóa đường và tam giác.
- Xiaolin Wu's line algorithm, phương pháp tương tự vẽ nhanh đường có ứng dụng phép khử răng cưa (tiếng Anh: antialiasing).
- Midpoint circle algorithm, giải thuật vẽ đường tròn tương tự.
Tham khảo[sửa]
- ↑ Paul E. Black. Dictionary of Algorithms and Data Structures, NIST. http://www.nist.gov/dads/HTML/bresenham.html
- Jack E. Bresenham, "Algorithm for computer control of a digital plotter", IBM Systems Journal, Vol. 4, No.1, January 1965, pp. 25–30
- "The Bresenham Line-Drawing Algorithm", by Colin Flanagan
- Michael Abrash's Graphics Programming Black Book a very optimized version of the algorithm in C and assembly for use in video games with complete details of its inner workings, written by Michael Abrash, pages 654-678 - ISBN 978-1-57610-174-2
Đọc thêm[sửa]
- Patrick-Gilles Maillot's Thesis an extension of the Bresenham line drawing algorithm to perform 3D hidden lines removal; also published in MICAD '87 proceedings on CAD/CAM and Computer Graphics, page 591 - ISBN 2-86601-084-1.
- Line Thickening by Modification To Bresenham's Algorithm, A.S. Murphy, IBM Technical Disclosure Bulletin, Vol. 20, No. 12, May 1978.
Liên kết ngoài[sửa]
- Implementation in C for TC's BGI library
- Analyze Bresenham's line algorithm in an online Javascript IDE
- Basic Graphics Programs
- The Bresenham Line-Drawing Algorithm by Colin Flanagan
- National Institute of Standards and Technology page on Bresenham's algorithm
- Calcomp 563 Incremental Plotter Information
- Implementations in Delphi
- 3D extension
- Bresenham 3D
- Bresenham Algorithm in Python