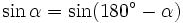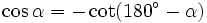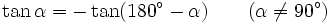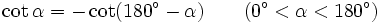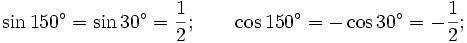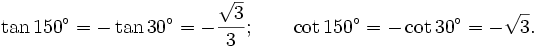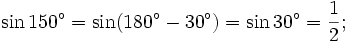Hình học 10/Chương II/§1. Giá trị lượng giác của một góc
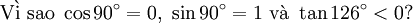
Mục lục
Lí thuyết[sửa]
Ở
lớp
9,
chúng
ta
đã
biết
các
tỉ
số
lượng
giác:
sin,
côsin,
tang,
côtang
của
một
góc
nhọn
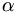 và
kí
hiệu
là
và
kí
hiệu
là
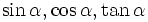 và
và
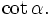 Ở
bài
này,
chúng
ta
sẽ
thấy
rằng,
các
tỉ
số
lượng
giác
đó
không
chỉ
áp
dụng
cho
các
góc
nhọn
(0°
<
α
<
90°)
mà
nó
còn
được
mở
rộng
để
áp
dụng
cho
các
góc
tù
(90°
<
α
<
180°).
Vậy
thì,
các
tỉ
số
lượng
giác
của
một
góc
nhọn
và
các
tỉ
số
lượng
giác
của
một
góc
tù
có
gì
giống
và
khác
nhau?
Ở
bài
này,
chúng
ta
sẽ
thấy
rằng,
các
tỉ
số
lượng
giác
đó
không
chỉ
áp
dụng
cho
các
góc
nhọn
(0°
<
α
<
90°)
mà
nó
còn
được
mở
rộng
để
áp
dụng
cho
các
góc
tù
(90°
<
α
<
180°).
Vậy
thì,
các
tỉ
số
lượng
giác
của
một
góc
nhọn
và
các
tỉ
số
lượng
giác
của
một
góc
tù
có
gì
giống
và
khác
nhau?
| Hoạt động 1 |
Cho
tam
giác
ABC
vuông
tại
A,
AB
=
c,
AC
=
b,
BC
=
a
và
góc
nhọn
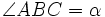 .
Tính
.
Tính
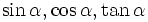 và
và
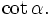
|
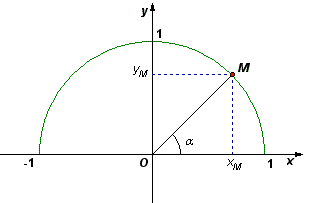
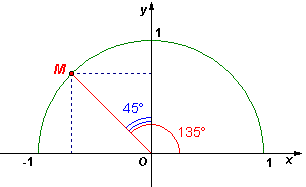
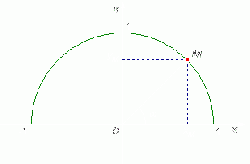
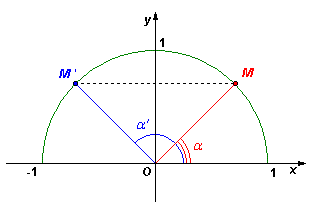
Trên hình 2.2 có một hệ tọa độ Oxy và một nửa đường tròn tâm O bán kính R = 1, nằm phía trên trục hoành. Ta gọi nó là nửa đường tròn đơn vị.
Nếu
cho
trước
một
góc
nhọn
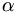 thì
ta
có
thể
xác
định
một
điểm
M
duy
nhất
trên
nửa
đường
tròn
đơn
vị
sao
cho
thì
ta
có
thể
xác
định
một
điểm
M
duy
nhất
trên
nửa
đường
tròn
đơn
vị
sao
cho
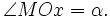
| Hoạt động 2 |
Giả
sử
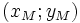 là
tọa
độ
của
điểm
M
(hình
2.2).
Hãy
chứng
tỏ
rằng:
là
tọa
độ
của
điểm
M
(hình
2.2).
Hãy
chứng
tỏ
rằng:
|
Bây
giờ
chúng
ta
mở
rộng
định
nghĩa
giá
trị
lượng
giác
cho
góc
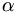 bất
kì
(0°
đến
180°).
Ta
có
định
nghĩa
sau
đây:
bất
kì
(0°
đến
180°).
Ta
có
định
nghĩa
sau
đây:
Định nghĩa[sửa]
|
Với
mỗi
góc
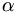 (0°
≤
(0°
≤
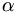 ≤
180°),
ta
xác
định
điểm
M
trên
nửa
đường
tròn
đơn
vị
sao
cho
≤
180°),
ta
xác
định
điểm
M
trên
nửa
đường
tròn
đơn
vị
sao
cho
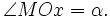 Giả
sử
điểm
M
có
tọa
độ
Giả
sử
điểm
M
có
tọa
độ
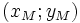 .
Khi
đó:
.
Khi
đó:
Tung
độ
Hoành
độ
Tỉ
số
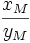 (với
(với
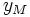 ≠
0)
gọi
là
côtang
của
góc
≠
0)
gọi
là
côtang
của
góc
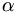 ,
kí
hiệu
là
,
kí
hiệu
là
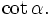
|
|
Các
số
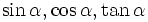 và
và
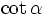 gọi
là
các
giá
trị
lượng
giác
của
góc
gọi
là
các
giá
trị
lượng
giác
của
góc
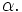
Như
vậy,
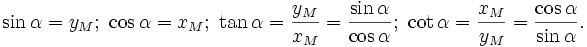
| VÍ DỤ 1 |
Tìm
các
giá
trị
lượng
giác
của
góc
135°.
|
| Lời giải | |
| Hoạt động 3 |
Xác
định
tọa
độ
của
điểm
M
trong
hình
2.2,
từ
đó
tìm
các
giá
trị
lượng
giác
của
góc
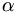 khi:
khi:
a)
|
Giá trị lượng giác của một số góc đặc biệt[sửa]
Bằng cách tính như trên, ta có thể tính được các giá trị lượng giác của một số góc đặc biệt mà ta cần ghi nhớ: 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150° và 180° (Các giá trị lượng giác này cũng có thể tìm thấy trong bảng số hoặc bằng máy tính bỏ túi).
Kết quả được cho trong bảng dưới đây.
| Góc |
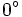 |
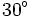 |
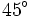 |
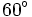 |
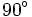 |
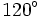 |
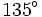 |
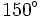 |
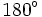 |
|---|---|---|---|---|---|---|---|---|---|
| sin |
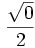 |
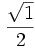 |
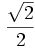 |
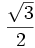 |
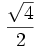 |
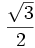 |
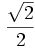 |
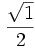 |
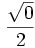 |
| cos |
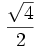 |
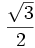 |
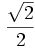 |
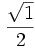 |
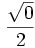 |
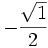 |
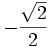 |
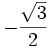 |
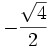 |
| tan | 0 |
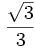 |
1 |
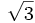 |
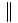 |
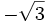 |
-1 |
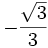 |
0 |
| cot |
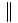 |
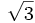 |
1 | 0 |
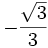 |
-1 |
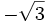 |
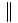 |
Trong
bảng,
kí
hiệu
"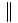 "
để
chỉ
giá
trị
lượng
giác
không
xác
định.
"
để
chỉ
giá
trị
lượng
giác
không
xác
định.
Dấu của các giá trị lượng giác[sửa]
Chúng ta đã biết, các tỉ số lượng giác của một góc nhọn luôn dương. Tuy nhiên, điều đó sẽ không còn đúng cho trường hợp của góc tù. Tại sao lại như vậy?
Xét hình 2.2, khi điểm M di chuyển trên nửa đường tròn thì dễ thấy rằng:
-
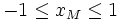 hay
hay
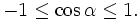
-
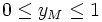 hay
hay
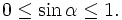
Từ đó, ta có bảng sau đây về dấu của các tỉ số lượng giác:
Như
vậy,
sin
của
góc
tù
luôn
dương
còn
côsin,
tang,
côtang
của
góc
tù
luôn
âm.
| Hoạt động 4 |
Điền
dấu
"x"
vào
ô
vuông
thích
hợp.
|
|||||||||||||||
Giá trị lượng giác của hai góc bù nhau[sửa]
Chúng ta đã biết mối quan hệ giữa các tỉ số lượng giác của hai góc phụ nhau: Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia. Liệu có một quan hệ tương tự, cho các giá trị lượng giác của hai góc bù nhau?
| Hoạt động 5 | |
Từ
đó
ta
suy
ra
các
tính
chất
sau
đây:
|
Nếu
hai
góc
bù
nhau
thì
sin
của
chúng
bằng
nhau,
côsin,
tang
và
côtang
của
chúng
đối
nhau;
nghĩa
là:
|
Ví
dụ
dưới
đây
minh
họa
cách
sử
dụng
mối
quan
hệ
trên
(của
hai
góc
bù
nhau)
để
tính
giá
trị
lượng
giác
của
các
góc
lớn
hơn
90°.
| VÍ DỤ 2 |
Tìm
các
giá
trị
lượng
giác
của
góc
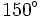 .
. |
| Lời giải |
Vì
góc
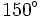 bù
với
góc
bù
với
góc
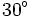 nên:
nên:
Cách
khác:
ta
cũng
viết
|
Sử dụng máy tính bỏ túi[sửa]
Ta cũng có thể sử dụng các loại máy tính bỏ túi để tính giá trị lượng giác của một góc khi biết số đo của góc và ngược lại, tính số đo của góc khi biết giá trị lượng giác của góc đó. Chẳng hạn đối với máy CASIO fx-500MS, ta có thể thực hiện như sau:
Tính giá trị lượng giác[sửa]
Sau khi mở máy, ấn phím MODE nhiều lần để màn hình hiện lên dòng chữ ứng với các số sau đây:
| Deg | Rad | Gra |
| 1 | 2 | 3 |
Sau
đó
ấn
phím
1
để
xác
định
đơn
vị
đó
góc
là
"độ"
và
tính
giá
trị
lượng
giác
của
góc.
Ví
dụ:
Tính
sin
60°52'41.
Giải
Ấn liên tiếp các phím sau đây:
| sin | 63 | o''' | 52 | o''' | 41 | o''' | = |
Ta
được
kết
quả
là:
sin
60°52'41''
≈
0,897859012
Để
tính
cos
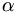 và
tan
và
tan
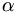 ta
cũng
làm
như
trên,
chỉ
thay
việc
ấn
phím
sin
bằng
phím
cos
hay
tan.
ta
cũng
làm
như
trên,
chỉ
thay
việc
ấn
phím
sin
bằng
phím
cos
hay
tan.
Tính số đo của góc[sửa]
Sau khi mở máy và chọn đơn vị đo góc, để tính góc x khi biết các giá trị lượng giác của góc đó, ta làm như ví dụ sau:
Ví
dụ:
Tìm
x
biết
sin
x
=
0,3502.
Giải
Ta ấn liên tiếp các phím sau đây:
| SHIFT | sin | 0.3502 | = | SHIFT | o''' |
và
được
kết
quả
là:
x
≈
20°29'58''.
Muốn tìm x khi biết cos x, tan x ta làm tương tự như trên, chỉ thay phím sin bằng phím cos hay tan.
BÀI TẬP[sửa]
1.
Xác
định
dấu
của
các
giá
trị
lượng
giác
của
góc
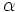 khi:
khi:
a)
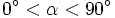
b)
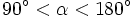
2.
Góc
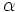 là
góc
tù
hay
góc
nhọn
để:
là
góc
tù
hay
góc
nhọn
để: |
|
a)
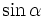 và
và
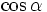 khác
dấu.
khác
dấu. |
b)
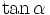 và
và
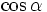 cùng
dấu.
cùng
dấu. |
c)
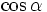 và
và
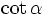 khác
dấu.
khác
dấu. |
d)
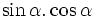 có
giá
trị
âm.
có
giá
trị
âm. |
e)
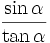 có
giá
trị
âm.
có
giá
trị
âm. |
f)
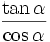 có
giá
trị
dương.
có
giá
trị
dương. |
3.
Tìm
góc
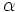 thỏa
mãn:
thỏa
mãn: |
|
a)
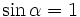
|
b)
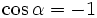
|
c)
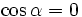
|
d)
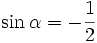
|
e)
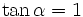
|
f)
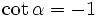
|
g)
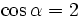
|
h) |
4.
Xác
định
vị
trí
của
điểm
M
trên
nửa
đường
tròn
đơn
vị
trong
mỗi
trường
hợp
sau
đây
(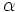 là
số
đo
của
góc
là
số
đo
của
góc
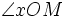 ):
): |
||
a)
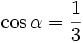
|
b)
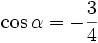
|
c)
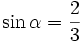
|
| 5. So sánh các cặp số sau đây: | |
a)
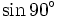 và
và
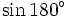
|
b)
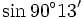 và
và
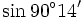
|
c)
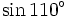 và
và
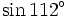
|
d)
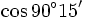 và
và
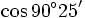
|
e)
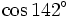 và
và
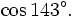
|
f) |
| 6. Tính giá trị các biểu thức sau: | |
a)
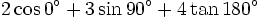
|
b)
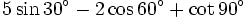
|
c)
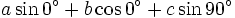
|
d)
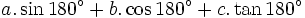
|
e)
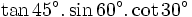
|
f)
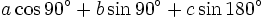
|
g)
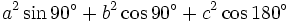
|
h)
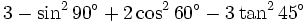
|
i)
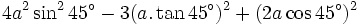
|
k)
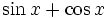 khi
x
bằng
0°;
45°;
60°
khi
x
bằng
0°;
45°;
60° |
l)
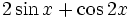 khi
x
bằng
60°;
45°;
30°.
khi
x
bằng
60°;
45°;
30°. |
m)
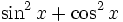 khi
x
bằng
30°;
45°;
60°;
90°;
145°.
khi
x
bằng
30°;
45°;
60°;
90°;
145°. |
7.
Chứng
minh
rằng
với
mọi
góc
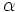 (0°
≤
(0°
≤
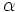 ≤
180°)
ta
đều
có
≤
180°)
ta
đều
có
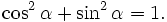
Cho
góc
x,
với
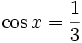 .
Tính
giá
trị
của
biểu
thức:
.
Tính
giá
trị
của
biểu
thức:
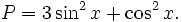
| 8. Chứng minh rằng: | ||
| a) sin105° = sin75°; | b) cos170° = -cos10°; | cos122° = -cos58°. |
| 9. Sử dụng máy tính, hãy tính các giá trị lượng giác sau, theo giá trị lượng giác của các góc bé hơn 90°: | |
a)
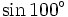
|
b)
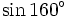
|
c)
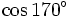
|
d)
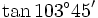
|
e)
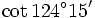
|
f) |
10.
Chứng
minh
rằng
trong
tam
giác
ABC
ta
có:
a) sin A = sin(B + C); b) cosA = -cos(B + C).
11.
Cho
AOB
là
tam
giác
cân
tại
O
có
OA
=
a
và
có
đường
cao
OH
và
AK.
Giả
sử
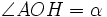 .
Tính
AK
và
OK
theo
a
và
.
Tính
AK
và
OK
theo
a
và
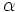 .
.
Xem thêm[sửa]
Tài liệu tham khảo[sửa]
-
Sách
in:
- Hình học 10, Nhà xuất bản Giáo dục, 2006, trang 35.
- Hình học 10 Nâng cao, Nhà xuất bản Giáo dục, 2006, trang 40. (Chưa khai thác hết)
- Hình học 10, Nhà xuất bản Giáo dục, 2001, trang 28. (Chưa khai thác hết)
- Tài liệu giáo khoa thí điểm, Hình học 10, Ban khoa học tự nhiên, Nhà xuất bản Giáo dục, 1996, trang 24.



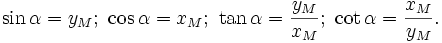
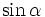 .
.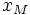 của
điểm
M
gọi
là
côsin
của
góc
của
điểm
M
gọi
là
côsin
của
góc
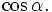
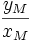 (với
(với
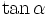 .
.
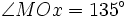 .
.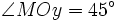 .
.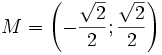
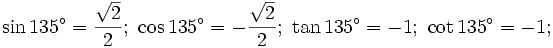
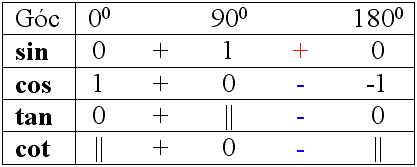
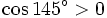

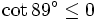
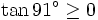
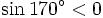
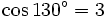
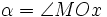 và
và
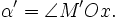
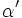 bằng
nhau
và
đối
nhau?
bằng
nhau
và
đối
nhau?