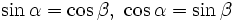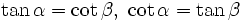Hình học 9/Chương I/§2. Tỉ số lượng giác của góc nhọn
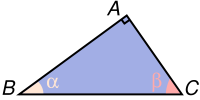
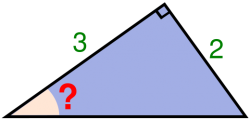
| Trong một tam giác vuông, nếu biết tỉ số độ dài của hai cạnh thì có biết được độ lớn của các góc nhọn hay không? |
Mục lục
Lí thuyết[sửa]
Tỉ số lượng giác của một góc nhọn là gì?[sửa]
Mở đầu[sửa]
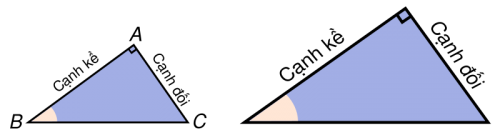
Cho tam giác ABC vuông tại A (hình 13). Xét góc nhọn B của nó, ta đã biết cạnh AB được gọi là cạnh kề của góc B, cạnh AC được gọi là cạnh đối của góc B.
Ta cũng đã biết: hai tam giác vuông đồng dạng với nhau khi và chỉ khi chúng có cùng số đo của một góc nhọn, hoặc các tỉ số giữa cạnh đối và cạnh kề của một góc nhọn trong mỗi tam giác đó là như nhau (hình 13). Như vậy, tỉ số giữa cạnh đối và cạnh kề của một góc nhọn trong tam giác vuông đặc trưng cho độ lớn của góc nhọn đó.
| Hoạt động 1 |
Xét
tam
giác
ABC
vuông
tại
A
có
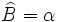 .
Chứng
minh
rằng:
.
Chứng
minh
rằng:
a)
b)
|
Ngoài
tỉ
số
giữa
cạnh
đối
và
cạnh
kề,
ta
còn
xét
các
tỉ
số
giữa
cạnh
kề
và
cạnh
đối,
cạnh
đối
và
cạnh
huyền,
cạnh
kề
và
cạnh
huyền
của
một
góc
nhọn
trong
tam
giác
vuông.
Các
tỉ
số
này
chỉ
thay
đổi
khi
độ
lớn
của
góc
nhọn
đang
xét
thay
đổi
và
ta
gọi
chúng
là
các
tỉ
số
lượng
giác
của
góc
nhọn
đó.
Định nghĩa[sửa]
Cho
góc
nhọn
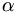 .
Vẽ
một
tam
giác
vuông
có
một
góc
nhọn
.
Vẽ
một
tam
giác
vuông
có
một
góc
nhọn
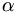 (ta
có
thể
vẽ
như
sau:
Vẽ
góc
(ta
có
thể
vẽ
như
sau:
Vẽ
góc
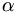 ,
từ
một
điểm
bất
kì
trên
một
cạnh
của
góc
,
từ
một
điểm
bất
kì
trên
một
cạnh
của
góc
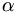 kẻ
đường
vuông
góc
với
cạnh
kia
(hình
14)),
xác
định
cạnh
đối
và
cạnh
kề
của
góc
kẻ
đường
vuông
góc
với
cạnh
kia
(hình
14)),
xác
định
cạnh
đối
và
cạnh
kề
của
góc
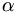 .
Khi
đó:
.
Khi
đó:
|
Tỉ
số
giữa
cạnh
đối
và
cạnh
huyền
được
gọi
là
sin
của
góc
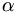 ,
kí
hiệu
,
kí
hiệu
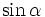 .
.
Tỉ
số
giữa
cạnh
kề
và
cạnh
huyền
được
gọi
là
côsin
của
góc
Tỉ
số
giữa
cạnh
đối
và
cạnh
kề
được
gọi
là
tang
của
góc
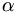 ,
kí
hiệu
,
kí
hiệu
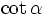 .
. |
|
Như
vậy:
NHẬN
XÉT:
Từ định nghĩa trên, dễ thấy các tỉ số lượng giác của một góc nhọn luôn dương. Hơn nữa, ta có:
-
-
-
-
-
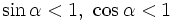 .
.
-
-
-
-
Cho
tam
giác
ABC
vuông
tại
A
có
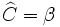 .
Hãy
viết
các
tỉ
số
lượng
giác
của
góc
.
Hãy
viết
các
tỉ
số
lượng
giác
của
góc
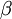 .
.
-
Như
vậy,
cho
góc
nhọn
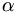 ,
ta
tính
được
các
tỉ
số
lượng
giác
của
nó.
Ngược
lại,
cho
một
trong
các
tỉ
số
lượng
giác
của
góc
nhọn
,
ta
tính
được
các
tỉ
số
lượng
giác
của
nó.
Ngược
lại,
cho
một
trong
các
tỉ
số
lượng
giác
của
góc
nhọn
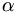 ,
ta
có
thể
dựng
được
góc
đó.
,
ta
có
thể
dựng
được
góc
đó.
Tỉ số lượng giác của hai góc phụ nhau[sửa]
| Hoạt động 4 | |
Từ
các
cặp
tỉ
số
bằng
nhau
đó,
ta
rút
ra:
Vì hai góc phụ nhau bao giờ cũng bằng hai góc nhọn của một tam giác vuông nào đó, nên ta có định lí sau đây về mối quan hệ giữa các tỉ số lượng giác của hai góc phụ nhau.
|
Nếu
hai
góc
phụ
nhau
thì
sin
góc
này
bằng
côsin
góc
kia,
tang
góc
này
bằng
côtang
góc
kia.
|
|
CHÚ Ý:
Từ
nay,
khi
viết
các
tỉ
số
lượng
giác
của
một
góc
nhọn
trong
tam
giác,
ta
bỏ
kí
hiệu
"^"
đi.
Chẳng
hạn,
viết
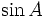 thay
cho
thay
cho
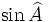 ,...
,...
BÀI TẬP[sửa]
Tài liệu tham khảo[sửa]
- Sách in: Toán 9, tập 1, Nhà xuất bản Giáo dục, 2006, trang 71.



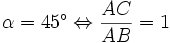 ;
;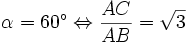 .
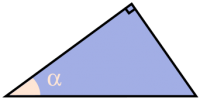
.
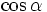 .
.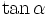 .
.