Hình học 10/Chuẩn kiến thức và kĩ năng
Mục lục
VECTƠ (13:0:1)[sửa]
Các định nghĩa[sửa]
| CHỦ ĐỀ | MỨC ĐỘ CẦN ĐẠT | GHI CHÚ |
|---|---|---|
|
|
Ví dụ. Cho hình bình hành ABCD, tâm O. Gọi M, N lần lượt là trung điểm của AD, BC.
a)
Kể
tên
hai
vectơ
cùng
phương
với
b)
Chỉ
ra
các
vectơ
bằng
vectơ
|
Tổng và hiệu của hai vectơ[sửa]
| CHỦ ĐỀ | MỨC ĐỘ CẦN ĐẠT | GHI CHÚ |
|---|---|---|
|
Cho bốn điểm A, B, C, D. Chứng minh rằng:
Cho tam giác đều ABC cạnh a. Tính độ dài các vectơ:
Cho sáu điểm M, N, P, Q, R, S tùy ý. Chứng minh rằng:
|
Tích của vectơ với một số[sửa]
| CHỦ ĐỀ | MỨC ĐỘ CẦN ĐẠT | GHI CHÚ |
|---|---|---|
|
|
Ví
dụ.
Gọi
M,
N
lần
lượt
là
trung
điểm
của
các
đoạn
thẳng
AB,
CD.
Chứng
minh
rằng:
Ví dụ. Cho hình bình hành ABCD. Chứng minh rằng: Ví dụ. Chứng minh rằng nếu G và G' lần lượt là trọng tâm của tam giác ABC và A'B'C' thì |
Trục tọa độ[sửa]
| CHỦ ĐỀ | MỨC ĐỘ CẦN ĐẠT | GHI CHÚ |
|---|---|---|
|
|
Ví
dụ.
Trên
một
trục
cho
các
điểm
A,
B,
M,
N
lần
lượt
có
tọa
độ
là:
a) Hãy biểu diễn các điểm đó trên trục. b) Hãy xác định độ dài đại số của các vectơ: |
Hệ trục tọa độ trong mặt phẳng[sửa]
| CHỦ ĐỀ | MỨC ĐỘ CẦN ĐẠT | GHI CHÚ |
|---|---|---|
|
|
Ví
dụ.
Cho
các
điểm:
a) Xác định tọa độ của điểm E đối xứng với A qua B. b) Xác định tọa độ trọng tâm G của tam giác ABC. |
TÍCH VÔ HƯỚNG CỦA HAI VECTƠ VÀ ỨNG DỤNG (12:0:0)[sửa]
Tích vô hướng[sửa]
| CHỦ ĐỀ | MỨC ĐỘ CẦN ĐẠT | GHI CHÚ |
|---|---|---|
|
|
Ví
dụ.
Cho
I
là
trung
điểm
của
đoạn
thẳng
AB.
Với
điểm
M
tùy
ý,
tính
Ví dụ. Chứng minh rằng với các điểm A, B, C tùy ý, ta luôn có: |
Các hệ thức lượng trong tam giác[sửa]
| CHỦ ĐỀ | MỨC ĐỘ CẦN ĐẠT | GHI CHÚ |
|---|---|---|
|
(trong đó R, r lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp tam giác; p là nửa chu vi tam giác).
|
Có giới thiệu công thức Hê-rông nhưng không chứng minh. Ví dụ. Chứng minh rằng: trong tam giác ABC ta có:
a)
b)
Ví dụ. Chứng minh rằng trong tam giác ABC ta có: Yêu cầu giải tam giác trong một số trường hợp đơn giản: tính được các cạnh và các góc còn lạ của tam giác khi biết ba yếu tố về cạnh và góc (chẳng hạn: cho trước độ dài ba cạnh; cho trước độ dài một cạnh và số đo của hai góc; cho trước độ dài hai cạnh và số đo của góc xen giữa của hai cạnh đó).
Ví
dụ.
Cho
tam
giác
ABC
có
Ví dụ. Hai địa điểm A, B cách nhau bởi một hồ nước (hình vẽ). Người ta lấy một địa điểm C và đo được góc BAC bằng 75°, góc BCA bằng 60°, đoạn AC dài 60m. Hãy tính khoảng cách từ A đến B. |
PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG (12:0:1)[sửa]
Phương trình đường thẳng[sửa]
| CHỦ ĐỀ | MỨC ĐỘ CẦN ĐẠT | GHI CHÚ |
|---|---|---|
|
|
Ví dụ. Viết phương trình tổng quát, phương trình tham số của đường thẳng trong mỗi trường hợp sau: a) Đi qua A(1;-2) và song song với đường thẳng 2x - 3y - 3 = 0. b) Đi qua hai điểm M(1;-1) và N(3;2). c) Đi qua điểm P(2;1) và vuông góc với đường thẳng x - y + 5 = 0.
a) Tính cosA. b) Tính khoảng cách từ điểm C đến đường thẳng AB. |
Phương trình đường tròn[sửa]
| CHỦ ĐỀ | MỨC ĐỘ CẦN ĐẠT | GHI CHÚ |
|---|---|---|
|
|
Ví dụ. Viết phương trình đường tròn có tâm I(1; -2) và a) đi qua điểm A(3;5). b) tiếp xúc với đường thẳng có phương trình x + y = 1. Ví dụ. Xác định tâm và bán kính của đường tròn có phương trình: Ví dụ. Cho đường tròn có phương trình: Viết phương trình tiếp tuyến của đường tròn tại điểm A(-1;0). |
Elip[sửa]
| CHỦ ĐỀ | MỨC ĐỘ CẦN ĐẠT | GHI CHÚ |
|---|---|---|
|
Từ phương trình chính tắc của elip:
xác định được:
|
Có giới thiệu về sự liên hệ giữa đường tròn và elip. Ví dụ. Tìm tọa độ các đỉnh và tiêu điểm của: 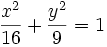 |
Xem thêm[sửa]
Tài liệu tham khảo[sửa]
-
Sách
in:
- Sách Giáo viên Hình học 10, Nhà xuất bản giáo dục, 2006, trang 14 (Trần Văn Hạo (Tổng Chủ biên), Nguyễn Mộng Hy (Chủ biên), Nguyễn Văn Đoành, Trần Đức Huyên).



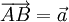 ,
với
vectơ
,
với
vectơ
 và
điểm
A
cho
trước.
và
điểm
A
cho
trước.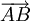 ,
hai
vectơ
cùng
hướng
với
,
hai
vectơ
cùng
hướng
với
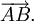
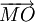 và
bằng
vectơ
và
bằng
vectơ
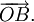
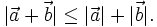
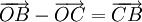 vào
chứng
minh
các
đẳng
thức
vào
chứng
minh
các
đẳng
thức
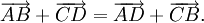
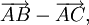
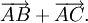
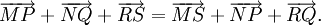
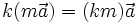
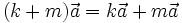
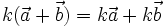
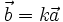 khi
cho
trước
số
k
và
vectơ
khi
cho
trước
số
k
và
vectơ
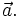
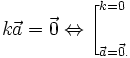
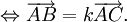
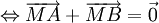
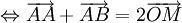 (với
điểm
O
bất
kì).
(với
điểm
O
bất
kì).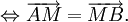
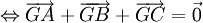
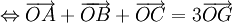 (với
điểm
O
bất
kì).
(với
điểm
O
bất
kì).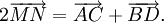
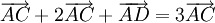
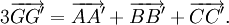
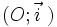 .
.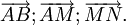
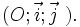
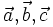 bất
kì:
bất
kì:
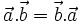
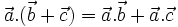
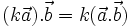
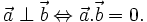
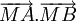 theo
AB
và
MI.
theo
AB
và
MI.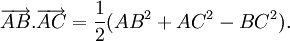
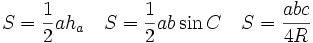
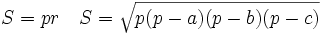
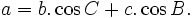
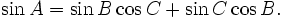
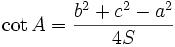
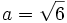 ;
b
=
2;
;
b
=
2;
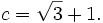 Tính
các
góc
A,
B,
bán
kính
R
của
đường
tròn
ngoại
tiếp
và
trung
tuyến
ma.
Tính
các
góc
A,
B,
bán
kính
R
của
đường
tròn
ngoại
tiếp
và
trung
tuyến
ma.
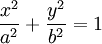 (a
>
b
>
0)
(a
>
b
>
0)

