Nhiệt động học lượng tử
Nhiệt động học là lĩnh vực cơ bản của vật lý nghiên cứu nhiệt năng, nhiệt độ và mối liên quan của chúng với năng lượng và công năng. Khi các nhà vật lý mở rộng các định luật nhiệt động học đến vùng lượng tử thì họ thiết lập được mối liên quan giữa năng lượng, entropy và lý thuyết thông tin. Đây thực chất là một cuộc cách mạng của nhiệt động học.[1]
Mục lục
Lý thuyết thông tin [2][sửa]
Mục tiêu của khoa học thông tin là lượng hóa thông tin và biến thông tin thành một khái niệm khoa học chính xác. Khoa học thông tin được áp dụng trong nhiều lĩnh vực khoa học (nhất là trong sinh học vốn đặt ra nhiều thách thức) và kinh tế học. Khoa học thông tin nhờ tính khái quát lớn của nó là một khoa học đầy hấp dẫn đối với các nhà khoa học.
Cần phải lượng hóa (quantifier) khái niệm thông tin. Nhiều nhà khoa học còn cho rằng thông tin là một trong những đại lượng vật lý cơ bản nhất, ngang hàng với năng lượng và thời gian.
Trong quá trình phát triển của khoa học thông tin đã xuất hiện hai bài báo quan trọng năm 1948: Một lý thuyết toán học của truyền thông (communication), của Claude Shannon, một kỹ sư Mỹ; và Điều khiển học (cybernetics) - điều khiển và truyền thông trong máy móc và sinh vật của Norbert Wiener, một nhà toán học Mỹ.
Lịch sử nhiệt động học: máy sử dụng hơi[sửa]
Năm 1824, kỹ sư người Pháp Sadi Carnot, 28 tuổi, viết cuốn: Reflections on the Motive Power of Fire. Trong cuốn sách này, ông đã tìm ra công thức mô tả hệ số hữu dụng trong một máy sử dụng hơi khi chuyển nhiệt và nhiệt năng. Nhiệt (một đại lượng hỗn độn - một dạng năng lượng khuếch tán) đã có thể trở thành công năng cơ học (một loại năng lượng có trật tự có khả năng đẩy một piston làm chuyển động một bánh xe). Carnot tìm thấy rằng hệ số hữu dụng của máy chỉ phụ thuộc vào hiệu nhiệt độ giữa nguồn nóng và bộ phận tiêu thụ nhiệt. Từ đó công sản ra là hệ quả của việc chuyển nhiệt từ một vật nóng sang vật lạnh hơn.
Carnot chết vì dịch tả 8 năm sau, không kịp nhìn thấy công thức hệ số hữu dụng của ông đã được phát triển thành nhiệt động học (NĐH) trong thế kỷ 19. Người ta thiết lập mối quan hệ giữa một loạt định luật nối liền nhiệt độ, nhiệt năng, công, năng lượng và entropy (một đại lượng mô tả sự truyền lan năng lượng từ một vật thể có năng lượng lớn đến một vật thể ít năng lượng hơn).
Các định luật NĐH không chỉ áp dụng cho các máy hơi mà được áp dụng cho mọi đối tượng: mặt trời, lỗ đen, các sinh vật và cho toàn thể vũ trụ. Theo Einstein, NĐH là một lý thuyết đơn giản và phổ quát của thế giới.
Một khối khí nằm ở một nhiệt độ cố định - như vậy không sản công được - song cũng có những hiệu nhiệt độ vi mô mà người ta có thể khai thác được.
Nhà vật lý thế kỷ 19 James Clerk Maxwell chỉ ra rằng ý niệm về sự khuếch tán nhiệt phụ thuộc vào trình độ tri thức của chúng ta.
Trong thời gian gần đây, một cách hiểu cách mạng về NĐH đã xuất hiện sử dụng lý thuyết thông tin lượng tử (quantum information theory) mô tả sự lan truyền thông tin trong các hệ lượng tử.
Tương tự như NĐH đã phát triển nhằm hoàn thiện máy sử dụng hơi thì giờ đây các nhà NĐH nghĩ đến các máy lượng tử. Họ muốn nới rộng NĐH vào thực tế lượng tử, và ở đây các khái niệm như nhiệt độ và công mang màu sắc mới và mất đi ý nghĩa thông thường.
Họ đã vén bức màn để lộ mối liên quan giữa năng lượng và thông tin.
NĐH lượng tử là một lĩnh vực mới.[3]
Với NĐH lượng tử, chúng ta đã đi vào một thế giới mới của NĐH - Sandu Popescu (Đại học Bristol) đã phát biểu như vậy.
Entropy - số đo của bất định[sửa]
Năm 1867, trong bức thư gửi bạn là Scotsman Peter Wait, Maxwell đã mô tả mối liên quan giữa NĐH và thông tin, liên quan đến định luật 2 của NĐH - định luật entropy tăng mãi (Arthur Eddington cho rằng định luật này là một định luật tối thượng của thiên nhiên). Theo định luật này, năng lượng càng ngày càng trở nên hỗn độn và càng ngày càng trở nên kém hiệu dụng khi lan truyền từ một vật nóng đến một vật lạnh và hiệu nhiệt độ giữa chúng càng giảm đi. (Hãy nhớ lại phát hiện của Carnot về vấn đề muốn có công sản ra cần một vật nóng và một vật lạnh).
Ludwig Boltzmann đã chỉ rằng năng lượng khuếch tán, entropy tăng lên đó chỉ là một hệ quả của thống kê: quả vậy có nhiều cách để năng lượng khuếch tán hơn là tập trung lại một chỗ như thế các hạt tiến đến nhiều trạng thái ở đấy năng lượng bị chia sẻ liên hồi.
Maxwell đưa ra khái niệm con quỷ Maxwell có khả năng vi phạm định luật 2 của NĐH: vật này biết được tọa độ và vận tốc của từng phân tử trong một cái hộp, nó phân hộp thành hai phần và tìm cách chuyển các phân tử nhanh về một phần và các phân tử chậm vào phần kia. Như vậy con quỷ phân chất khí thành hai phần nóng và lạnh và như vậy làm giảm entropy và chất khí trước kia không sản được công bây giờ đã có khả năng sản công nếu xét đến lượng tử.
Con quỷ Maxwell[sửa]
Con quỷ này là một sinh vật nhỏ tưởng tượng có khả năng tách những phân tử nhanh ra khỏi những phân tử chậm, như vậy từ một chất khí đồng nhất nó có thể tạo ra hai miền với nhiệt độ khác nhau (Hình 2).

Con quỷ Maxwell là hình ảnh của một vấn đề lớn: đó là việc thu nhận thông tin liên quan đến sự giảm entropy.
Con quỷ Maxwell trong sinh học[4] [5][sửa]
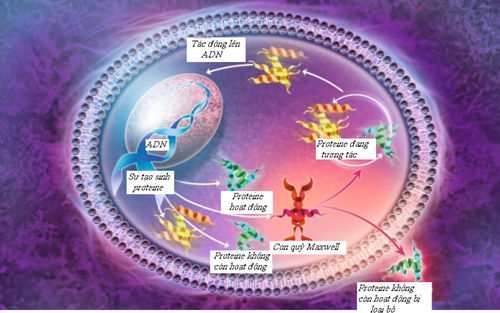
Theo A.Dauchin cần cầu cứu đến con quỷ Maxwell để hiểu vấn đề: nhờ đâu một tế bào thu nhận thông tin có khả năng phản kháng lại (contrer) những hiệu ứng già hóa và sau đó tự tái tạo? Vì rằng một tế bào có thể chứa những con quỷ phân tử có khả năng phân biệt các protein bình thường với những protein không còn hoạt động nữa và loại những tế bào sau (Hình 3).
Mối liên quan này giữa thông tin và entropy được nghiên cứu tiếp bởi nhà vật lý người Hung Leo Szilard năm 1929 và ông đã thử tính xem entropy tăng lên bao nhiêu khi con quỷ Maxwell thu được thông tin về các phân tử. Ông đã thu được biểu thức kBln2(kB là hằng số Boltzmann).
Muốn xác định lượng thông tin chứa trong một thông điệp có một độ dài nào đó chứa nhiều chữ hay ký tự, Claude Shannon tìm cách lượng hóa tính bất định (tức sự thiếu thông tin so với bản gốc) của những thông điệp khả dĩ khác có cùng độ dài và cùng sử dụng các chữ hay ký tự như trong bản gốc. Giả sử số thông điệp khả dĩ như vậy bằng N và xác suất chọn thông điệp thứ i là pi với p1 + p2 + ... + pN = 1. Shannon tìm ra hàm số H (p1,..., pN) mô tả sự bất định gắn với các khả năng. Shannon chứng minh rằng hàm H (gọi là entropy thông tin) bằng -K (p1logp1 + p2logp2 +... pN logpN), trong đó K là một hằng số. Nếu tất cả pi = 0 ngoại trừ một p nào đó thì sự bất định (incertitude) = 0, vì ta chỉ còn một bản gốc. Nếu tất cả p bằng nhau thì H = Klog(1/p) và ta có biểu thức của entropy. Khi thông điệp chỉ chứa hai số 0 hoặc 1 (bit) thì p1 = p2= 1/2 và lúc này H = Klog2.
Công thức - K(p1logp1 + p2logp2 + ... pN logpN) rất giống công thức entropy trong cơ học thống kê của Ludwig Boltzmann và Josiah Gibbs, chỉ cần lấy log và cho K là hằng số Boltzmann. Đại lượng pi chính là xác suất của trạng thái vi mô i của hệ. Sự đồng nhất entropy - thông tin của Shannon với entropy của Boltzmann - Gibbs được kiểm nghiệm bởi nhiều nhà khoa học.
Maxwell và nhiều người khác đã cho chúng ta thấy rằng một định luật của thiên nhiên có thể phụ thuộc và tri thức (sâu hay cạn) của chúng ta về tọa độ và vận tốc của các phân tử.
Như vậy định luật 2 của NĐH phụ thuộc vào thông tin chủ quan của chúng ta.
Một thế kỷ sau, nhà vật lý Mỹ Charles Bennett (cùng với Leo Szilard và Rolf Landauer) giải quyết nghịch lý trên bằng cách hình thức nối liền NĐH với ngành khoa học non trẻ lý thuyết thông tin. Theo Bennett, tri thức của con quỷ nằm trong bộ nhớ của nó và bộ nhớ cần phải xóa đi và như vậy đòi hỏi công. (Năm 1961, Landauer tính ra rằng cần 2,9 zeptojoules năng lượng để xóa một bit thông tin trên máy tính). Nói cách khác, nếu con quỷ bố trí lại cho chất khí có vùng lạnh và nóng và như thể làm giảm entropy thì nó lại phải tạo nhiều hơn entropy để bù trừ. Và tổng entropy vẫn tăng đúng theo định luật 2 của NĐH.
Các phát hiện đó chứng tỏ như Landauer chỉ ra rằng “thông tin là vật lý”, nếu chúng ta có càng nhiều thông tin thì chúng ta có thể lấy ra được nhiều công. Con quỷ Maxwell có thể sản công từ một chất khí có một nhiệt độ nhất định nhờ nó có nhiều thông tin hơn là một người sử dụng thông thường.
Trong những thập kỷ qua, Popescu cùng các đồng nghiệp chứng tỏ rằng năng lượng truyền từ một vật nóng bởi vì có những lộ trình thông tin giữa các hạt. Theo thuyết lượng tử, tính chất vật lý các hạt mang tính xác suất; thay vì có thể miêu tả bằng số 1 hay số không thì chúng phải được mô tả bằng xác suất là 1 hay xác suất là 0 cùng thời. Khi hạt tương tác, chúng liên đới lượng tử với nhau (entangled). Trạng thái hiện nay của vũ trụ là lưu lại mọi thông tin của quá khứ.
***
Qua thời gian khi số hạt tăng lên và tương tác với nhau thông tin về các trạng thái của chúng lan truyền và được chia sẻ với ngày càng nhiều hạt. Popescu cho rằng mũi tên của sự tăng liên đới lượng tử là cơ sở của sự tăng entropy - mũi tên NĐH của thời gian. Một cốc cà phê nguội đi vì các phân tử cà phê va chạm với những phân tử của không khí, thông tin giam giữ trong năng lượng của chúng sẽ bị chia sẻ với không khí bên ngoài.
Việc hiểu entropy như là một số đo chủ quan cho phép vũ trụ toàn bộ tiến triển mà không mất thông tin.
Mười lăm năm sau, chúng ta nghĩ đến entropy như là một tính chất của một hệ NĐH (Renato Renner, Đại học ETH Zurich, Thụy Sĩ), chúng ta không nói rằng entropy là một tính chất của hệ mà phải là một tính chất xuất phát từ người quan sát hệ.
Renner nói rằng năng lượng có hai dạng nhiệt năng vô dụng và công hữu dụng, đó là ý niệm về các máy sử dụng hơi.
Các nhà công nghệ máy lượng tử sẽ nói gì?[sửa]
Janet Anders, một nhà vật lý nghiên cứu thông tin lượng tử (Đại học Exter), đề cập đến vấn đề công nghệ đối với NĐH lượng tử. Anders và đồng nghiệp nghiên cứu các định luật chế ngự các dịch chuyển lượng tử (quantum transitions) trong các máy lượng tử và các tủ lạnh lượng tử.
Kết luận[sửa]
Việc lượng tử hóa nhiệt động học là một vấn đề mới mẻ đầy hấp dẫn. NĐH lượng tử đã cho ta thấy thông tin là một đại lượng vật lý cơ bản quan trọng như năng lượng và entropy và liên quan đến hai đại lượng đó.
NĐH lượng tử sẽ mở nhiều triển vọng cho công nghệ chế tạo những máy lượng tử.
Tài liệu tham khảo[sửa]
- ↑ Natalie Wolchover,The Quantum Thermodynamics Revolution https://www.quantamagazine.org/quantum-thermodynamics-revolution/
- ↑ Jérome Segal,La théorie de l’information existe-t-elle? Pour la Science số tháng 2/2013.
- ↑ V. Vedral, Decoding reality – The Universe as quantum Information, Oxford University Press, 2010.
- ↑ P. M. Binder et A. danchin, Life’s demons: information and orderin biology, EMBO Reports, vol. 12 (6), pp. 495-499, 2011.
- ↑ H. Yockey, Information Theory and Molecular biology, Cambridge University Press, 1992.
Nguồn[sửa]
- Cao Chi, Tạp chí Tia sáng






