Sách:Điện từ sinh học/Các hệ thống điện tâm đồ khác
17.1. Chuyển động lưỡng cực
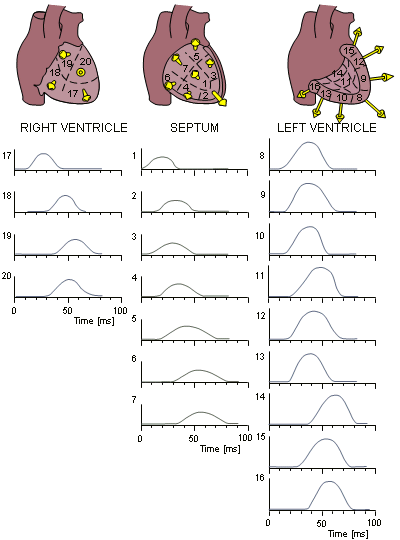
Chúng ta cần chú ý rằng nguồn kết hợp với hoạt động của tim là một lớp kép, mà nó nằm ngay tại bề mặt hoạt động. Lớp kép này xấp xỉ một lưỡng cực. Tương tự như phần hoạt động trong các quá trình xử lý thành tâm thất, lưỡng cực nằm tại vùng trung tâm lực hấp dẫn của vỏ bọc bên ngoài gần ống giác, cũng di chuyển. Do đó vị trí lưỡng điện cực của giũa rãnh di chuyển.
Tuy nhiên nếu có nhiều hơn một sóng hoạt động tại cùng một thời điểm thì chuyển động này sẽ là một hàm phức của sự chuyển động của các lưỡng cực tổng đơn lẻ. Khi chúng ta cố gắng phát triển mô hình đối với bộ tạo điện áp của tim thì lưỡng cực chuyển động là một mục tiêu cần quan tâm mang tính logic. R. M. Arthur đã dẫn ra các thí nghiệm để đánh giá lưỡng cực chuyển động này. Trong các lần thí nghiệm đó ông đã sử dụng mô hình thuần nhất hữu hạn đối với thân người. Nó chỉ ra rằng phần trung tâm chuyển động của hoạt động tim là nằm bên trong đường biên qua một chu trình hoạt động của tim, trong tâm nhĩ là dạng sóng P và dạng sóng QSR và T.
Sự xem xét kỹ lưỡng hơn vào bên trong mô hình lưỡng cực chuyển động thu được một vài kết quả gần đây là nhờ quá trình làm việc của Pierre Savard và các đồng nghiệp. Các nghiên cứu này đã sử dụng mô hình động vật để nghiên cứu nên các hình chiếu có thể được tính toán và so sánh với những dữ liệu trong thành tim. Họ thu được những kết quả tốtnhất của họ khi mới chỉ giới hạn làm phóng xạ bề mặt, một kết quả không bất ngờ. Sau đây chúng ta sẽ cùng xem xét hai mô hình lưỡng cực chuyển động dưới đây.
17.2. Các lưỡng cực kép
Khẳng định đầu tiên đối với mô hình lưỡng cực của tim được tạo ra bởi E. J. Fischmann và M. R. Barber. Dựa trên ý tưởng này, Ronald Selvester đã cấu tạo nên mô hình tính toán của 20 lưỡng cực. Trong mô hình đầu tiên, ảnh hưởng của vùng tiếp giáp ngực và tính không đẳng hướng bên trong đã bị bỏ quên. Selvester sau đó đã tạo ra một mô hình khác mà trong mô hình này các tác động trên đều được nhắc đến.
J. H. Holt và các đồng sự đã tạo ra một mô hình gồm 12 lưỡng cực mà các vùng phân bố và các hướng đã được cố định.Để tính toán các lưỡng cực này, ông ghi các tín hiệu điện tim từ một mảng gồm 126 điện cực đặt trên bề mặt ngực. Số lượng các điện cực đã được chọn lựa để nhằm tạo ra một biên độ lớn hơn so với số lượng các biến trong mô hình đa lưỡng cực. Bước tiến này đã cung cấp một cơ hội để cải thiện một cách chính xác dựa trên những dư thừa và bù lại cho các tín hiệu đã mất và cho việc chống lại sự hiện diện của nhiễu.
17.3. Đa cực
Mô hình đa cực dựa trên sự giãn nở điều hòa theo hình cầu của nguồn khối và các thành phần của nó là các lưỡng cực, mạng 4 cực, mạng tám cực, v.v… Các thành phần này của mô hình đa cực có một số lượng biến độc lập là 3 đối với lưỡng cực, 5 đối với 4 cực, 7 đối với tám cực, v.v… Những kiến thức khoa học đầu tiên được cung cấp mô hình đa cực cho mô hình tim đã được G. Yeh và các đồng sự thực hiện. Việc nghiên cứu với các mô hình đa cực đã được David Geselowitz và Daniel Brody thực hiện.
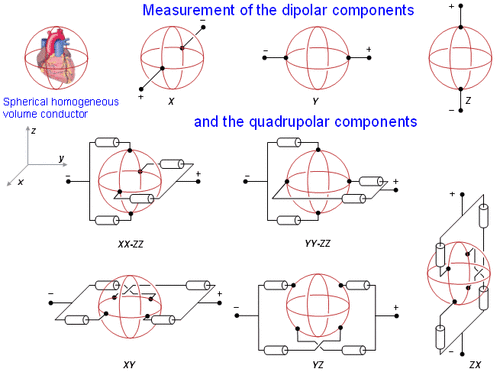
Hình 17.2 miêu tả nguyên lý cơ bản liên quan tới quá trình đo các thành phần lưỡng cực và bốn cực của nguồn nằm trong một khối dẫn dạng cầu. Trong thực tế, thay cho các điện trở trọng số, có rất nhiều các điện cực được sử dụng và các thành phần đa cực được tính toán theo số học. Thủ thuật này được thảo luận ở Pilkington và Plonsey.
Trong quá trình nghiên cứu của ông R.M.Arthur, khi ông cố gắng điều chỉnh mô hình lưỡng cực với mức điện thế được đo là 284 điểm trên bề mặt ngực chỉ ra rằng sự điều chỉnh tốt nhất chỉ ra một mức lỗi là 23%. Khi thành phần bốn cực được thêm vào mô hình thì sự điều chỉnh hiệu quả nhất chỉ ra với mức lỗi là 14%. Như vậy, việc thêm vào thành phần 4 cực đã làm cho sai số giảm đi 9%.
Một sự mô tả chi tiết hơn củacác mô hình tim trình bày ở đây à quan trọng và đánh giá của các thế mạnh và điểm yếu có thể được tìm thấy trong Pilkington và Plonsey (1982) và trong Gulrajani (1989). Như đã lưu chú, đó là sự phát triển trong việc sử dụng đa nhiều điện cực trên bề mặt cơ thể (khoảng 25-250) và sử dụng các kết quả được hiển thị để tạo một chuỗi các bản đồ bề mặt đẳng thế ..
17.4. Tổng kết về đạo trình điện tim đồ
Chúng ta đã mô tả một cách ngắn gọn khả năng tính toán hiệu suất chẩn đoán của điện tim đồ bằng cách cải thiện các mô hình của nguồn và bộ dẫn được thực hiện thông qua các quá trình điều tra được bàn luận ở trên. Sau đây, chúng ta sẽ định nghĩa các khái niệm về độ nhạy, nét đặc trưng và hiệu suất chẩn đoán.
Độ nhạy chỉ ra một số lượng tương đối nhiều các hiện tượng bất thường được hệ thống phát hiện. Nét đặc trưng chỉ ra một số lượng tương đối các hiện tượng bình thường mà nó được phân loại là các chuẩn. Khái niệm về hiệu suất chẩn đoán được định nghĩa như là một giá trị trung bình của độ nhạy và nét đặc trưng của phương pháp sự dụng. Chúng ta tổng kết các định nghĩa này như dưới đây:
Độ chính xác=(số hien tượng bất thường được xác định)/(tổng số hiện tượng bất thường)*100%=TP/(TP+FN)*100% (17.1)
Độ đặc trưng=(số hien tượng bình thường được xác định)/(tổng số hiện tượng bình thường)*100%=TP/(TP+FP)*100 (17.2)
Hiệu suất chuẩn đoán=(độ nhạy+độ dặc trưng)/2 (17.3)
Trong
đó:
FN= Điện tích âm sai
FP= Điện tích dương sai
TN= Điện tích âm đúng
TP= Điện tích dương đúng
Sự diều tra của Holt,dựa trên mô hình đa lưỡng cực,đưa lại nhiều kết quả rất đáng chú ý. Trong việc chuẩn đoán chứng phì đại chính xác khoảng 90%. Tuy nhiên chuẩn đoán bệnh cơ tim chính xác chỉ khoảng 80%. Do đó, mặc dù rất phức tạp nhưng nó đã không đạt được kết quả tốt hơn so với phương pháp tiếp cận đơn giản quy ước.
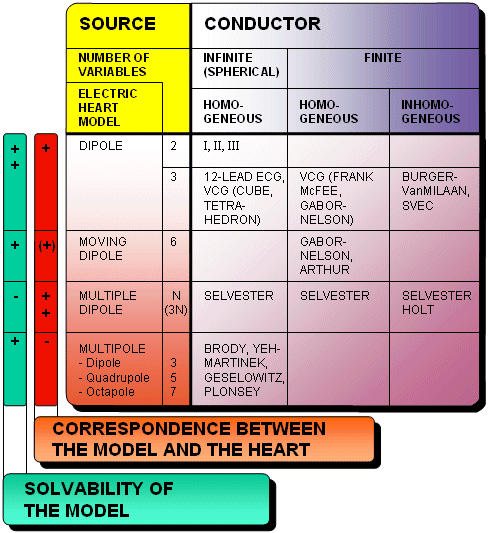
Bảng 17.1 tổng quan các nguồn và các mô hình dẫn dựa trên các hệ thống ECG và nghiên cứu về nó. Một cách tự nhiên sẽ lựa chọn mô hình chính xác các ngồn tốt như các mô hình dẫn. Vì vậy sự lựa chọn mô hình tiếp cận sẽ giúp định hướng đúng và là một trong những cột thấp nhất trong bảng 17.1.
Trong bộ phận 7.5.4,nó được chú thích rằng bất kỳ mô hình nào cũng tốt như nhau đối với sự điều chế sinh lý học. Áp dụng nguyên lý này để lựa chọn mô hình đa lưỡng cực, vì nó mô phỏng mỗi khoảng cơ tim.
Thành phần của mô hình đa lưỡng cực là trực giao và chỉ ra duy nhất một đáp án; tuy nhiên nó rất khó để đưa ra khái niệm về sinh lý học. Một hướng mở, người ta có thể tính toán một mô hình đa điện cực cũng như ba hay bốn điện cực rất ít nhiễu và lỗi trong hình học. Nhưng vấn đề là gần đúng (không chính xác). Hơn nữa, việc giải thích của một lưỡng cực ngược trong các trạng thái mặt dưới tế bào là không rõ ràng và có lẽ cũng không phải duy nhất. Về cơ bản, vấn đề ngược với vấn đề nguồn bên trong không phải là duy nhất, nói tóm lại đó là các các vấn đề bên dưới của các giải pháp ngược trong điện tim đồ. Vì lý do này, hiển nhiên rằng mô hình lưỡng cực đơn vẫn giữ vị trí trung tâm trong lĩnh vực điện tim đồ lâm sàng.
Những năm gần đây một số thuật toán phức tạp được áp dụng để giải quyết vấn đề trong điện tâm đồ. Giờ đây tạp trung dữ liệu từ hệ thống bao gồm một lượng lớn các điện cực(100-200) . Một sự tăng cường, mục tiêu có nhiều thông tin trong công trình hơn, bị giới hạn bởi một số điện thế bề mặt thượng vị xác định. Trong nguyên lý này xác định duy nhất một điện thế bề mặt cơ thể và họ cũng cung cấp thêm thông tin vùng tăng cường. Các phương pháp tiếp cận khác nhau sử dụng cách khác nhau để ổn định những gì là điều kiện xấu (bao gồm các ma trận điều kiện xấu nghịch đảo). Các phương pháp phụ thuộc vào sự giới hạn ưu tiên sinh lý như sự lan truyền bên ngoài về các đặc tính quang phổ và biên độ của nhiễu, độ nhẵn (độ trơn) của sự phân bố điện thế, hoặc độ nhẵn của độ dốc / Laplacians.
Bạn đọc có thể coi ba ấn phẩm: Pilkington and Plonsey (1982), Gulrajani (1988; 1989), and Rudy and Messinger-Rapport (1988).
Tham khảo
-Arthur RM, Geselowitz DB, Briller SA, Trost RF (1971): The path of the electrical center of the human heart determined from surface electrocardiograms. J. Electrocardiol. 4:(1) 29-33. -
-Arthur RM, Geselowitz DB, Briller SA, Trost RF (1972): Quadrupole components of the human surface electrocardiogram. Am. Heart J. 83:(5) 663-7.
-Brody DA, Bradshaw JC, Evans JW (1961): A theoretical basis for determining heart-lead relationships of the equivalent cardiac multipole. IRE Trans. Biomed. Electron. BME-8:(4) 139-43.
-Fischmann EJ, Barber MR (1963): 'Aimed' electrocardiography. Model studies, using a heart consisting of 6 electrically isolated areas. Am. Heart J. 65:(5) 628-37.
-Geselowitz DB (1960): Multipole representation for an equivalent cardiac generator. Proc. IRE 48:(1) 75-9.
-Gulrajani RM (1989): The inverse problem of electrocardiography. In Comprehensive Electrocardiology. Theory and
-Practice in Health and Disease, 1st ed. Vol. 1, ed. PW Macfarlane, TDV Lawrie, pp. 237-88, Pergamon Press, New York.
-Gulrajani RM, Savard P, Roberge FA (1988): The inverse problem in electrocardiography: Solution in terms of equivalent sources. CRC Crit. Rev. Biomed. Eng. 16: 171-214.
-Holt JH, Barnard ACL, Lynn MS, Svendsen P (1969): A study of the human heart as a multiple dipole electrical source. I. Normal adult male subjects. Circulation 40:(Nov) 687-96.
-Holt JH, Barnard CL, Lynn MS (1969): A study of the human heart as a multiple dipole electrical source. II.
-Diagnosis and quantitation of left ventricular hypertrophy. Circulation 40:(Nov) 697-710.
-Holt JH, Barnard CL, Lynn MS, Kramer JO (1969): A study of the human heart as a multiple dipole electrical source. III. Diagnosis and quantitation of right ventricular hypertrophy. Circulation 40:(Nov) 711-8.
-Lynn MS, Barnard ACL, Holt JH, Sheffield LT (1967): A proposed method for the inverse problem in electrocardiology. Biophys. J. 7:(6) 925-45.
-Macfarlane PW, Lawrie TDV (1989): The normal electrocardiogram and vectorcardiogram. In Comprehensive
-Electrocardiology: Theory and Practice in Health and Disease, 1st ed. Vol. 1, ed. PW Macfarlane, TDV Lawrie, pp. 407-57, Pergamon Press, New York.
-Pilkington TC, Plonsey R (1982): Engineering Contributions to Biophysical Electrocardiography, 248 pp. IEEE Press, John Wiley, New York.
-Rudy Y, Messinger-Rapport B (1988): The inverse problem of electrocardiography. Solutions in terms of epicardial potentials. CRC Crit. Rev. Biomed. Eng. 16: 215-68.
-Savard P, Roberge FA, Perry J-B, Nadeau RA (1980): Representation of cardiac electrical activity by a moving dipole for normal ectopic beats in the intact dog. Circ. Res. 46:(3) 415-25.
-Selvester RH, Collier CR, Pearson RB (1965): Analog computer model of the vectorcardiogram. Circulation 31:(1) 45-53.
-Selvester RH, Kalaba R, Collier CR, Bellman R, Kagiwada H (1966): A mathematical model of the electric field of the heart with distance and boundary effects. In Proc. Long Island Jewish Hosp. Symposium: Vectorcardiography 1965, ed. I Hoffman, pp. 403-10, North-Holland Publishing, Amsterdam.
-Yeh GCK, Martinek J, Beaumont H (1958): Multipole representation of current generators in a volume conductor.
-Bull. Math. Biophys. 20:(1) 203-14.
Một số sách khác:
-Macfarlane,PW and Lawrie,TDV (eds.) (1989): Comprehensive Electrocardiology: Theory and Practice in Health and Disease. 1st ed. Vols. 1, 2, and 3. Pergamon Press, New York. 1785 p
| Trang trước | Các hệ thống điện tâm đồ khác | Trang tiếp |