Sách:Điện từ sinh học/Các hệ thống đạo trình tâm đồ véc tơ
16.1.Giới thiệu
![]() Trong
cuốn
bài
viết
đầu
tiên
về
điện
tâm
đồ
của
con
người
xuất
bản
năm
1887,Augustus
D.
Waller
chỉ
ra
tính
chất
lưỡng
cực
của
nguồn
phát
tín
hiệu
điện
tim
(Waller,
1887;
xem
Hình
1.17).Bởi
vì
nó
có
thể
mô
tả
nguồn
phát
điện
tim
của
tim
một
cách
khá
đúng
đắn
với
một
lưỡng
cực
tương
đương,được
gọi
là
vectơ
điện
tâm
đồ
(EHV),một
cách
tự
nhiên
để
hiện
thị
nó
dưới
dạng
vectơ.Sự
đo
lường
và
hiển
thị
của
điện
tâm
đồ
vecto
được
gọi
là
ghi
điện
tâm
đồ
vecto
vectorcardiograph
(VCG),
hoặc
vectorelectrocardiography
(VECG)
để
phân
biệt
nó
với
ghi
từ
tâm
đồ
vecto
vectormagnetocardiography.
Trong
cuốn
bài
viết
đầu
tiên
về
điện
tâm
đồ
của
con
người
xuất
bản
năm
1887,Augustus
D.
Waller
chỉ
ra
tính
chất
lưỡng
cực
của
nguồn
phát
tín
hiệu
điện
tim
(Waller,
1887;
xem
Hình
1.17).Bởi
vì
nó
có
thể
mô
tả
nguồn
phát
điện
tim
của
tim
một
cách
khá
đúng
đắn
với
một
lưỡng
cực
tương
đương,được
gọi
là
vectơ
điện
tâm
đồ
(EHV),một
cách
tự
nhiên
để
hiện
thị
nó
dưới
dạng
vectơ.Sự
đo
lường
và
hiển
thị
của
điện
tâm
đồ
vecto
được
gọi
là
ghi
điện
tâm
đồ
vecto
vectorcardiograph
(VCG),
hoặc
vectorelectrocardiography
(VECG)
để
phân
biệt
nó
với
ghi
từ
tâm
đồ
vecto
vectormagnetocardiography.
![]() Về
lý
thuyết,một
cách
rõ
ràng
để
hiển
thị
đáp
ứng
của
lưỡng
cực
là
với
một
máy
hiện
sóng
(oscilloscope
)
theo
quỹ
đạo
của
các
điểm
đầu
cuối
của
các
vectơ
được
chiếu
lên
mặt
phẳng
cơ
sở.Sự
hiển
thị
này
được
gọi
là
không
gian
điện
tâm
đồ
vecto.Điều
này
được
minh
hoạ
trong
Hình
16.1.Hệ
thống
sắp
xếp
vuông
góc
đó
là
sự
lựa
chọn
tự
nhiên.Hệ
trục
toạ
độ
đó
có
thể
hoặc
là
hệ
trục
cơ
thể
hoặc
là
hệ
trục
tim.
Về
lý
thuyết,một
cách
rõ
ràng
để
hiển
thị
đáp
ứng
của
lưỡng
cực
là
với
một
máy
hiện
sóng
(oscilloscope
)
theo
quỹ
đạo
của
các
điểm
đầu
cuối
của
các
vectơ
được
chiếu
lên
mặt
phẳng
cơ
sở.Sự
hiển
thị
này
được
gọi
là
không
gian
điện
tâm
đồ
vecto.Điều
này
được
minh
hoạ
trong
Hình
16.1.Hệ
thống
sắp
xếp
vuông
góc
đó
là
sự
lựa
chọn
tự
nhiên.Hệ
trục
toạ
độ
đó
có
thể
hoặc
là
hệ
trục
cơ
thể
hoặc
là
hệ
trục
tim.
![]() Cái
đó
có
thể
hiển
thị
thông
tin
về
thới
gian
(
thang
đo
thời
gian
)
bởi
sự
điều
chỉnh
cường
độ
của
chùm
sáng
máy
hiện
sóng
để
quỹ
đạo
là
gián
đoạn
có
chu
kì
(
có
thể
1
khoảng
2
ms).Bởi
sự
điều
chỉnh
cường
độ
máy
hiện
sóng
với
một
sóng
dạng
tam
giác,mỗi
khoảng
2
ms
có
một
sóng
hình
giọt
nước
đề
biết
hướng
của
quỹ
đạo.
Cái
đó
có
thể
hiển
thị
thông
tin
về
thới
gian
(
thang
đo
thời
gian
)
bởi
sự
điều
chỉnh
cường
độ
của
chùm
sáng
máy
hiện
sóng
để
quỹ
đạo
là
gián
đoạn
có
chu
kì
(
có
thể
1
khoảng
2
ms).Bởi
sự
điều
chỉnh
cường
độ
máy
hiện
sóng
với
một
sóng
dạng
tam
giác,mỗi
khoảng
2
ms
có
một
sóng
hình
giọt
nước
đề
biết
hướng
của
quỹ
đạo.
![]() Sóng
cũng
có
thể
được
hiển
thị
bởi
việc
chỉ
ra
ba
thành
phần
vectơ
như
một
hàm
của
thời
gian.Sự
hiển
thị
này
được
gọi
là
vector
điện
tâm
đồ
vô
hướng,bởi
nó
cung
cấp
thông
tin
trống
rằng
không
hiển
thị
vô
hướng
của
12
đạo
trình
ECG.
Sóng
cũng
có
thể
được
hiển
thị
bởi
việc
chỉ
ra
ba
thành
phần
vectơ
như
một
hàm
của
thời
gian.Sự
hiển
thị
này
được
gọi
là
vector
điện
tâm
đồ
vô
hướng,bởi
nó
cung
cấp
thông
tin
trống
rằng
không
hiển
thị
vô
hướng
của
12
đạo
trình
ECG.
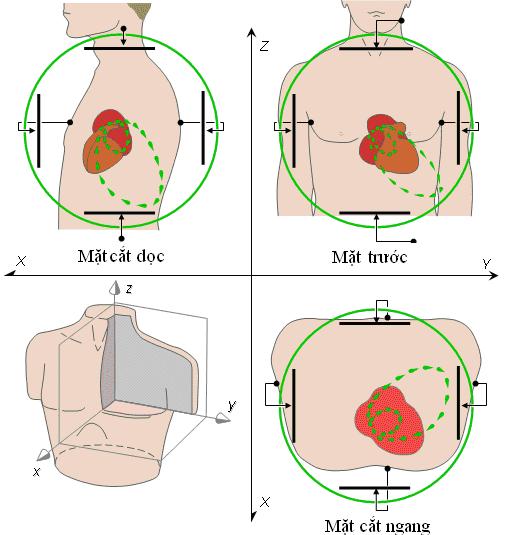
Hình 16.1 Những nguyên tắc cơ bản của điện tâm đồ vecto được minh hoạ dựa trên ý tưởng kết hợp các trường đạo trình trực giao với nhau được thiết lập song song đối diện nhau trên thân ( cấu hình lưỡng cực ).
![]() Đó
là
cả
hệ
thống
đạo
trình
VCG
chưa
hiệu
chỉnh(không
chính
xác
)
và
đã
hiệu
chỉnh(chính
xác).Hệ
thống
VCG
chưa
hiệu
chỉnh
không
xem
xét
đến
sự
biến
dạng
gây
ra
bởi
các
đường
bao
quanh
và
bởi
tính
không
đồng
nhất
bên
trong
cơ
thể.Hệ
thống
đạo
trình
chưa
hiệu
chỉnh
giả
thiết
rằng
hướng
của
các
đường
nối
trong
không
gian
của
một
cặp
điện
cực
cung
cấp
sự
định
hướng
của
các
vectơ
đạo
trình
tương
đương.Hiện
nay
đã
được
biết
đến
sự
giả
thiết
này
là
không
chính
xác,sẽ
được
tranh
luận
sau.Trong
bất
kỳ
dụng
cụ
nào,các
hệ
thống
đạo
trình
chưa
hiệu
chỉnh
không
còn
sử
dụng
trong
y
tế
lâm
sàng.
Đó
là
cả
hệ
thống
đạo
trình
VCG
chưa
hiệu
chỉnh(không
chính
xác
)
và
đã
hiệu
chỉnh(chính
xác).Hệ
thống
VCG
chưa
hiệu
chỉnh
không
xem
xét
đến
sự
biến
dạng
gây
ra
bởi
các
đường
bao
quanh
và
bởi
tính
không
đồng
nhất
bên
trong
cơ
thể.Hệ
thống
đạo
trình
chưa
hiệu
chỉnh
giả
thiết
rằng
hướng
của
các
đường
nối
trong
không
gian
của
một
cặp
điện
cực
cung
cấp
sự
định
hướng
của
các
vectơ
đạo
trình
tương
đương.Hiện
nay
đã
được
biết
đến
sự
giả
thiết
này
là
không
chính
xác,sẽ
được
tranh
luận
sau.Trong
bất
kỳ
dụng
cụ
nào,các
hệ
thống
đạo
trình
chưa
hiệu
chỉnh
không
còn
sử
dụng
trong
y
tế
lâm
sàng.
![]() Mục
đích
của
hệ
thống
đạo
trình
đã
hiệu
chỉnh
là
để
thực
hiện
một
phép
đo
trực
giao
giữa
các
vecto
điện
tâm
đồ.Trong
một
phép
đo
trực
giao
cả
hai
điều
sau
đây
đều
là
yêu
cầu
để
hoàn
thành:
Mục
đích
của
hệ
thống
đạo
trình
đã
hiệu
chỉnh
là
để
thực
hiện
một
phép
đo
trực
giao
giữa
các
vecto
điện
tâm
đồ.Trong
một
phép
đo
trực
giao
cả
hai
điều
sau
đây
đều
là
yêu
cầu
để
hoàn
thành:
![]() 1.Ba
thành
phần
được
đo
của
vectơ
điện
tâm
đồ
là
trực
giao
và
hướng
của
hệ
trục
tọa
độ
(tức
là,các
vectơ
đạo
trình
song
song
với
hệ
trục
tọa
độ,mà
thường
là
hệ
trục
cơ
thể
).Hơn
nữa,mỗi
trường
đạo
trình
là
thống
nhất
trong
cả
trái
tim.
1.Ba
thành
phần
được
đo
của
vectơ
điện
tâm
đồ
là
trực
giao
và
hướng
của
hệ
trục
tọa
độ
(tức
là,các
vectơ
đạo
trình
song
song
với
hệ
trục
tọa
độ,mà
thường
là
hệ
trục
cơ
thể
).Hơn
nữa,mỗi
trường
đạo
trình
là
thống
nhất
trong
cả
trái
tim.
![]() 2.Mỗi
một
trong
ba
thành
phần
của
vectơ
điện
tâm
đồ
phát
hiện
được
với
độ
nhạy
tương
ứng,có
nghĩa
là
,sự
đo
lường
là
chuẩn
hoá.
2.Mỗi
một
trong
ba
thành
phần
của
vectơ
điện
tâm
đồ
phát
hiện
được
với
độ
nhạy
tương
ứng,có
nghĩa
là
,sự
đo
lường
là
chuẩn
hoá.
![]() Trong
hệ
thống
đạo
trình
điện
tâm
đồ
đã
được
chuẩn
hoá,tính
chính
xác
của
phép
đo
trực
giao
được
giới
hạn
bởi
phương
pháp
áp
dụng
lý
thuyết.Phương
pháp
lý
thuyết
cho
việc
phân
tích
nguồn
khối
và
chất
dẫn
khối
đã
được
thảo
luận
dễ
dàng
ở
Chương
9.Mỗi
một
trong
số
chúng
đã
được
cho
phép
một
hệ
thống
VCG
trở
nên
trực
giao
với
giới
hạn
của
việc
thực
hiện
chỉnh
sửa.Hệ
thống
đạo
trình
này
sẽ
được
thảo
luận
chi
tiết
sau
ở
chương
này.Điều
quan
trọng
lâm
sàng
của
phép
ghi
điện
tim
đồ
là
gì?Câu
trả
lời
là
nội
dung
thông
tin
của
VCG
là
giống
như,một
cách
đại
khái,như
là
của
đạo
trình
V2,V6,
và
aVf
trong
hệ
thống
12
đạo
trình,mặc
dù
nó
được
thu
dưới
dạng
chính
xác
(trực
giao
).Đó
là
sự
thật
rằng
nội
dung
thông
tin
trong
sóng
VCG
là
tốt
hơn
trong
ECG
vô
hướng.Ngoài
ra,hệ
thống
hiển
thị
cung
cấp
một
cơ
hội
để
phân
tích
quá
trình
của
sự
hoạt
động
chính
diện
với
một
cách
thức
khác,đặc
biệt
là
phần
đầu
và
phần
cuối
của
nó.Nó
cũng
dễ
hơn
nhiều
đề
quan
sát
hướng
của
các
điện
tâm
đồ
vecto
từ
các
chu
kì
VCG.Ngoài
ra,phạm
vi
của
vòng
lặp,cái
mà
không
dễ
dàng
quan
sát
được
từ
sự
hiển
thị
vô
hướng
,có
thể
có
tầm
quan
trọng
lâm
sàng.
Trong
hệ
thống
đạo
trình
điện
tâm
đồ
đã
được
chuẩn
hoá,tính
chính
xác
của
phép
đo
trực
giao
được
giới
hạn
bởi
phương
pháp
áp
dụng
lý
thuyết.Phương
pháp
lý
thuyết
cho
việc
phân
tích
nguồn
khối
và
chất
dẫn
khối
đã
được
thảo
luận
dễ
dàng
ở
Chương
9.Mỗi
một
trong
số
chúng
đã
được
cho
phép
một
hệ
thống
VCG
trở
nên
trực
giao
với
giới
hạn
của
việc
thực
hiện
chỉnh
sửa.Hệ
thống
đạo
trình
này
sẽ
được
thảo
luận
chi
tiết
sau
ở
chương
này.Điều
quan
trọng
lâm
sàng
của
phép
ghi
điện
tim
đồ
là
gì?Câu
trả
lời
là
nội
dung
thông
tin
của
VCG
là
giống
như,một
cách
đại
khái,như
là
của
đạo
trình
V2,V6,
và
aVf
trong
hệ
thống
12
đạo
trình,mặc
dù
nó
được
thu
dưới
dạng
chính
xác
(trực
giao
).Đó
là
sự
thật
rằng
nội
dung
thông
tin
trong
sóng
VCG
là
tốt
hơn
trong
ECG
vô
hướng.Ngoài
ra,hệ
thống
hiển
thị
cung
cấp
một
cơ
hội
để
phân
tích
quá
trình
của
sự
hoạt
động
chính
diện
với
một
cách
thức
khác,đặc
biệt
là
phần
đầu
và
phần
cuối
của
nó.Nó
cũng
dễ
hơn
nhiều
đề
quan
sát
hướng
của
các
điện
tâm
đồ
vecto
từ
các
chu
kì
VCG.Ngoài
ra,phạm
vi
của
vòng
lặp,cái
mà
không
dễ
dàng
quan
sát
được
từ
sự
hiển
thị
vô
hướng
,có
thể
có
tầm
quan
trọng
lâm
sàng.
![]() Ở
chương
này
chúng
tôi
giới
thiệu
các
ví
dụ
tiêu
biểu
trong
số
lớn
hệ
thống
ghi
điện
tim
các
đạo
trình
chưa
hiệu
chỉnh
và
đã
hiệu
chỉnh.
Ở
chương
này
chúng
tôi
giới
thiệu
các
ví
dụ
tiêu
biểu
trong
số
lớn
hệ
thống
ghi
điện
tim
các
đạo
trình
chưa
hiệu
chỉnh
và
đã
hiệu
chỉnh.
16.2 Hệ thống đạo trình điện tâm đồ vecto chưa hiệu chỉnh
ĐIỀU KIỆN ĐẦU :
NGUỒN: Lưỡng cực điện ở một vị trí cố định
VẬT DẪN:Không xác định,vật dẫn khối đồng nhất và hình cầu đồng chất với lưỡng cực trong trung tâm của nó ( giải pháp thông thường ).
16.2.1 Điện tim đồ đơn cực bởi Mann
![]() Mặc
dù
Waller
là
người
đầu
tiên
ghi
lại
3
đạo
trình
trực
giao
gần
nhất,cụ
thể
là
miệng
đến
tay
trái,miệng
tới
chân
trái
và
phía
sau
ra
phía
trước,ông
đã
không
hiển
thị
chúng
ở
dạng
vectơ.Đó
là
Hubert
Mann
người
đầu
tiên
đề
xuất
khái
niệm
về
vectơ
điện
não
đồ
bằng
việc
cho
ra
đời
một
máy
điện
tim
đồ
đơn
(monocardiogram
)
vào
năm
1920,cái
mà
ông
đã
xây
dựng
thủ
công
từ
đạo
trình
các
chi
của
Einthoven,được
hiển
thị
ở
hình
1.18
(Mann,1920).Điện
tim
đồ
đơn
của
Mann
là
một
hình
chiếu
của
các
vòng
vectơ
ở
bề
mặt
phía
trước,việc
giả
định
tính
hợp
lí
của
các
vectơ
đạo
trình
tam
giác
Einthoven
cái
mà
nó
sử
dụng
để
giải
thích
điện
áp
đạo
trình
chân
tay.Vì
vậy,nó
chỉ
có
hai
chiều,và
nó
không
bao
gồm
thông
tin
quay
trở
lại
bề
mặt
từ
các
mặt
dọc
và
ngang.(Chú
ý
rằng
Mann
đã
đặt
các
tín
hiệu
của
các
đạo
trình
I,II
và
III
đến
vectơ
các
đạo
trình
trong
chiều
phân
cực
đối
ngược.Vì
vậy,vòng
vectơ
được
định
hướng
lên
trên
và
phải,mặc
dù
trên
thực
tế
nên
chuyển
hướng
xuống
và
trái
).
Mặc
dù
Waller
là
người
đầu
tiên
ghi
lại
3
đạo
trình
trực
giao
gần
nhất,cụ
thể
là
miệng
đến
tay
trái,miệng
tới
chân
trái
và
phía
sau
ra
phía
trước,ông
đã
không
hiển
thị
chúng
ở
dạng
vectơ.Đó
là
Hubert
Mann
người
đầu
tiên
đề
xuất
khái
niệm
về
vectơ
điện
não
đồ
bằng
việc
cho
ra
đời
một
máy
điện
tim
đồ
đơn
(monocardiogram
)
vào
năm
1920,cái
mà
ông
đã
xây
dựng
thủ
công
từ
đạo
trình
các
chi
của
Einthoven,được
hiển
thị
ở
hình
1.18
(Mann,1920).Điện
tim
đồ
đơn
của
Mann
là
một
hình
chiếu
của
các
vòng
vectơ
ở
bề
mặt
phía
trước,việc
giả
định
tính
hợp
lí
của
các
vectơ
đạo
trình
tam
giác
Einthoven
cái
mà
nó
sử
dụng
để
giải
thích
điện
áp
đạo
trình
chân
tay.Vì
vậy,nó
chỉ
có
hai
chiều,và
nó
không
bao
gồm
thông
tin
quay
trở
lại
bề
mặt
từ
các
mặt
dọc
và
ngang.(Chú
ý
rằng
Mann
đã
đặt
các
tín
hiệu
của
các
đạo
trình
I,II
và
III
đến
vectơ
các
đạo
trình
trong
chiều
phân
cực
đối
ngược.Vì
vậy,vòng
vectơ
được
định
hướng
lên
trên
và
phải,mặc
dù
trên
thực
tế
nên
chuyển
hướng
xuống
và
trái
).
![]() Mann
cũng
đã
xây
dựng
một
điện
kế
gương
đặc
biệt
cho
phép
hiển
thị
điện
tâm
đồ
đơn
một
cách
trực
tiếp
từ
tín
hiệu
ECG;xem
Hình
16.2
(
Mann
,1938a).Gương
điện
kế
này
bao
gồm
ba
cuộn
dây
được
sắp
xếp
trên
một
mặt
phẳng
và
được
đặt
cách
đều
nhau
là
120o
xung
quanh
một
gương.Chúng
được
đặt
trong
một
từ
trường
cố
định
được
sản
xuất
bởi
một
cuộn
dây
lớn.Khi
ba
cuộn
dây
đó
được
điều
khiển
bởi
khuyếch
đại
tín
hiệu
điện
tim
ECG
từ
các
đạo
trình
I,II
và
III,mạng
lưới
moment
của
bộ
phận
cuộn
dây
này
được
sản
xuất
bằng
một
độ
lệch
của
gương,và
một
tia
sáng
của
nó
phản
xạ,tương
ứng
với
điện
tâm
đồ
vecto.Vì
vậy
điện
kế
gương
Mann
là
một
máy
tính
tương
tự
thực
sự
tính
toán
điện
tâm
đồ
đơn
từ
ba
đạo
trình
chân
tay.Công
việc
của
Mann
phần
lớn
đã
bị
bỏ
qua
trong
vòng
15
năm.Nó
đã
phải
chờ
đợi
sự
phát
minh
của
ống
tia
Catot
trong
năm
1930
khi
nó
đã
có
thể
áp
dụng
thiết
bị
điện
để
hiện
thị
phép
chiếu
của
vòng
vectơ
(Mann,1931,1938s).
Mann
cũng
đã
xây
dựng
một
điện
kế
gương
đặc
biệt
cho
phép
hiển
thị
điện
tâm
đồ
đơn
một
cách
trực
tiếp
từ
tín
hiệu
ECG;xem
Hình
16.2
(
Mann
,1938a).Gương
điện
kế
này
bao
gồm
ba
cuộn
dây
được
sắp
xếp
trên
một
mặt
phẳng
và
được
đặt
cách
đều
nhau
là
120o
xung
quanh
một
gương.Chúng
được
đặt
trong
một
từ
trường
cố
định
được
sản
xuất
bởi
một
cuộn
dây
lớn.Khi
ba
cuộn
dây
đó
được
điều
khiển
bởi
khuyếch
đại
tín
hiệu
điện
tim
ECG
từ
các
đạo
trình
I,II
và
III,mạng
lưới
moment
của
bộ
phận
cuộn
dây
này
được
sản
xuất
bằng
một
độ
lệch
của
gương,và
một
tia
sáng
của
nó
phản
xạ,tương
ứng
với
điện
tâm
đồ
vecto.Vì
vậy
điện
kế
gương
Mann
là
một
máy
tính
tương
tự
thực
sự
tính
toán
điện
tâm
đồ
đơn
từ
ba
đạo
trình
chân
tay.Công
việc
của
Mann
phần
lớn
đã
bị
bỏ
qua
trong
vòng
15
năm.Nó
đã
phải
chờ
đợi
sự
phát
minh
của
ống
tia
Catot
trong
năm
1930
khi
nó
đã
có
thể
áp
dụng
thiết
bị
điện
để
hiện
thị
phép
chiếu
của
vòng
vectơ
(Mann,1931,1938s).
![]() Một
phát
minh
thú
vị
trong
máy
đo
việc
ghi
vectơ
điện
tim
là
ống
tia
Catot
của
W.Hollan
và
H.F.
Hollan
(1939).Họ
đã
sử
dụng
ba
cặp
bản
bố
trí
lệch
nhau
60o
với
sự
tách
rời
nhau
tương
ứng
với
các
hướng
của
ba
canh
của
tam
giác
Einhoven
(
xem
Hình
16.3
).Khi
độ
lệch
các
bản
đó
được
điều
khiển
với
khuyếch
đại
các
đạo
trình
I,II
và
III,ống
tia
đã
sản
xuất
trong
màn
hình
một
điện
tâm
đồ
đơn
tương
tự
với
điện
kế
gương
Mann
trên
phim.
Một
phát
minh
thú
vị
trong
máy
đo
việc
ghi
vectơ
điện
tim
là
ống
tia
Catot
của
W.Hollan
và
H.F.
Hollan
(1939).Họ
đã
sử
dụng
ba
cặp
bản
bố
trí
lệch
nhau
60o
với
sự
tách
rời
nhau
tương
ứng
với
các
hướng
của
ba
canh
của
tam
giác
Einhoven
(
xem
Hình
16.3
).Khi
độ
lệch
các
bản
đó
được
điều
khiển
với
khuyếch
đại
các
đạo
trình
I,II
và
III,ống
tia
đã
sản
xuất
trong
màn
hình
một
điện
tâm
đồ
đơn
tương
tự
với
điện
kế
gương
Mann
trên
phim.
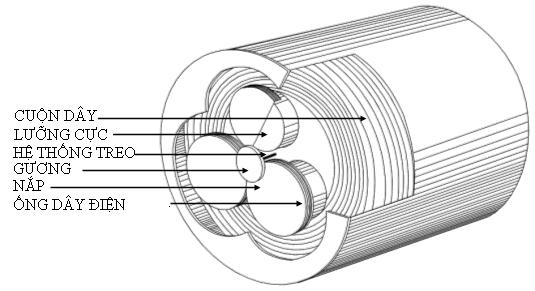
Hình 16.2 Điện tâm đồ vecto chuẩn trực xây dựng bởi Hubert Mann là công cụ đầu tiên để sản xuất được một sơ đồ điện tâm đồ vecto.Nó có ba cuộn dây được đặt một cách đối xứng cách nhau 120o xung quanh 1 gương.Vì vậy nó sản xuất 1 sơ đồ vectơ điện tim trên bề mặt phía trước từ ba đạo trình chân tay của Einhoven. (Mann,1938a ).
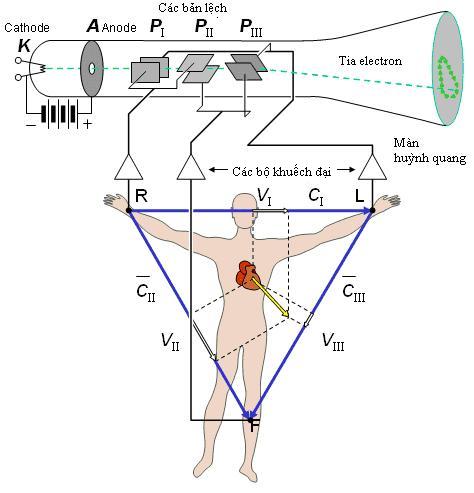
Hình 16.3 Ống tia Catot của W. Hollman và H. F. Hollman có ba cặp bản lệch định hướng theo hướng của ba cạnh của tam giác Einhoven.Vì vậy nó sản xuất sơ đồ điện tâm đồ trên bề mặt phía trước từ các đạo trình chân tay Einhoven (Hollman và Hollman ,1938)
16.2.2 Hệ thống đạo trình dựa trên hệ trục cơ thể vuông góc
![]() Hầu
hết
các
hệ
thống
đạo
trình
điện
tâm
đồ
vecto
chưa
hiệu
chỉnh
và
đã
hiệu
chỉnh
dựa
trên
trong
hệ
trục
cơ
thể
vuông
góc.Từ
số
lượng
lớn
của
các
hệ
thống
đạo
trình
VCG
chưa
hiệu
chỉnh,chúng
ta
đề
cập
đến
tóm
tắt
ngay
sau
trong
phần
này.
Hầu
hết
các
hệ
thống
đạo
trình
điện
tâm
đồ
vecto
chưa
hiệu
chỉnh
và
đã
hiệu
chỉnh
dựa
trên
trong
hệ
trục
cơ
thể
vuông
góc.Từ
số
lượng
lớn
của
các
hệ
thống
đạo
trình
VCG
chưa
hiệu
chỉnh,chúng
ta
đề
cập
đến
tóm
tắt
ngay
sau
trong
phần
này.
![]() Sau
khi
phát
minh
điểm
cực
trung
tâm
năm
1932,Frank
Norman
Wilson
một
cách
logic
đã
tiến
tới
sự
phát
triển
của
một
hệ
thống
đạo
trình
điện
tâm
đồ
vecto.Wilson
và
các
cộng
sự
phát
hiện
ra
một
hệ
thống
đạo
trình
được
thêm
vào
các
đạo
trình
chân
tay
của
Einhoven
một
điện
cực
xác
định
ở
phía
sau
(khoảng
2.5
cm
bên
trái
từ
đốt
sống
lưng
thứ
7
)(Wilson
và
Johnston
,1938,Wilson
,Johnston,
và
Kossmann
1947
).Bốn
điện
cực
tạo
thành
một
tứ
diện,như
được
hiển
thị
ở
Hình
16.4,và
các
kết
quả
có
được
cho
phép
thành
phần
quay
lại
bề
mặt
của
vectơ
trung
tâm
được
công
nhận.Ba
thành
phần
của
điện
tâm
đồ
vecto
được
đo
như
sau
(diễn
tả
trong
các
hệ
thống
phối
hợp
nhất
quán
được
mô
tả
trong
Phụ
lục
):Thành
phần
x
được
đo
giữa
điện
cực
ở
mặt
sau
và
điểm
trung
tâm
Wilson.Thành
phần
y
là
đạo
trình
I,và
thành
phần
z
là
đạo
trình
VF.Hệ
thống
đạo
trình
này,được
gọi
là
Tứ
diện
Wilson,là
hệ
thống
đầu
tiên
hiển
thị
ba
thành
phần
của
điện
tâm
đồ
vecto.
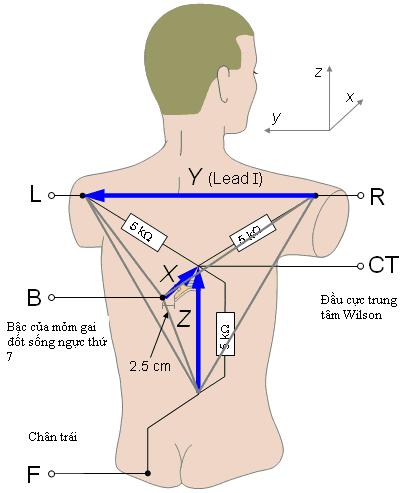
Sau
khi
phát
minh
điểm
cực
trung
tâm
năm
1932,Frank
Norman
Wilson
một
cách
logic
đã
tiến
tới
sự
phát
triển
của
một
hệ
thống
đạo
trình
điện
tâm
đồ
vecto.Wilson
và
các
cộng
sự
phát
hiện
ra
một
hệ
thống
đạo
trình
được
thêm
vào
các
đạo
trình
chân
tay
của
Einhoven
một
điện
cực
xác
định
ở
phía
sau
(khoảng
2.5
cm
bên
trái
từ
đốt
sống
lưng
thứ
7
)(Wilson
và
Johnston
,1938,Wilson
,Johnston,
và
Kossmann
1947
).Bốn
điện
cực
tạo
thành
một
tứ
diện,như
được
hiển
thị
ở
Hình
16.4,và
các
kết
quả
có
được
cho
phép
thành
phần
quay
lại
bề
mặt
của
vectơ
trung
tâm
được
công
nhận.Ba
thành
phần
của
điện
tâm
đồ
vecto
được
đo
như
sau
(diễn
tả
trong
các
hệ
thống
phối
hợp
nhất
quán
được
mô
tả
trong
Phụ
lục
):Thành
phần
x
được
đo
giữa
điện
cực
ở
mặt
sau
và
điểm
trung
tâm
Wilson.Thành
phần
y
là
đạo
trình
I,và
thành
phần
z
là
đạo
trình
VF.Hệ
thống
đạo
trình
này,được
gọi
là
Tứ
diện
Wilson,là
hệ
thống
đầu
tiên
hiển
thị
ba
thành
phần
của
điện
tâm
đồ
vecto.
![]() Hệ
thống
đạo
trình
của
F.Schellong
,S.Heller
và
G.Schwinggel
(1973)
là
hai
chiều,hiển
thị
ba
vòng
vecto
chỉ
ở
trên
bề
mặt
phía
trước.Những
hệ
thống
đạo
trình
khác
–của
Noburo
Kimura
(1939),Pierre
Duschosal
và
R.Sulzer
(1949),A.Grishman
và
L.Scherlis
(1952),
và
William
Milnor,S.Talbot
,và
E.Newman
(1953)-
cũng
cung
cấp
3
chiều.Những
hệ
thống
đạo
trình
này
được
minh
họa
ở
Hình
16.5.Bời
hình
học
của
chúng,hệ
thống
đạo
trình
của
Grishman
và
Scherlis
được
gọi
là
“hình
lập
phương
Grishman”
và
hệ
thống
đạo
trình
của
Duchosal
và
Schultzer
được
gọi
là
“lập
phương
kép
“.
Hệ
thống
đạo
trình
của
F.Schellong
,S.Heller
và
G.Schwinggel
(1973)
là
hai
chiều,hiển
thị
ba
vòng
vecto
chỉ
ở
trên
bề
mặt
phía
trước.Những
hệ
thống
đạo
trình
khác
–của
Noburo
Kimura
(1939),Pierre
Duschosal
và
R.Sulzer
(1949),A.Grishman
và
L.Scherlis
(1952),
và
William
Milnor,S.Talbot
,và
E.Newman
(1953)-
cũng
cung
cấp
3
chiều.Những
hệ
thống
đạo
trình
này
được
minh
họa
ở
Hình
16.5.Bời
hình
học
của
chúng,hệ
thống
đạo
trình
của
Grishman
và
Scherlis
được
gọi
là
“hình
lập
phương
Grishman”
và
hệ
thống
đạo
trình
của
Duchosal
và
Schultzer
được
gọi
là
“lập
phương
kép
“.
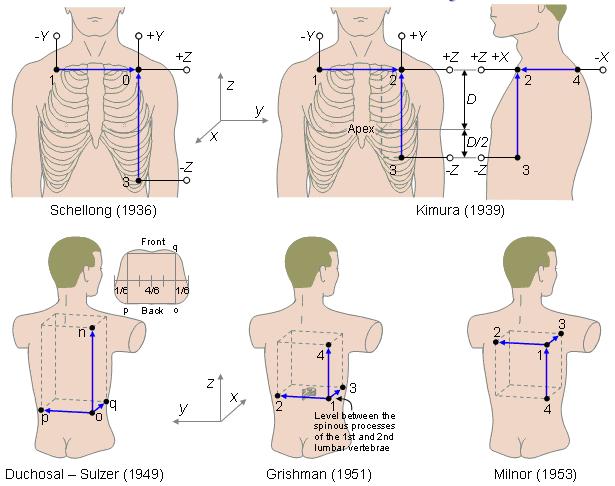
![]() Hình
16.5
Hệ
thống
đạo
trình
VCG
chưa
hiệu
chỉnh
dựa
trên
hệ
trục
cơ
thể
vuông
góc.
Hình
16.5
Hệ
thống
đạo
trình
VCG
chưa
hiệu
chỉnh
dựa
trên
hệ
trục
cơ
thể
vuông
góc.
16.2.3 Các hệ thống đạo trình VCG Akulinichev
![]() Ivan
T.Alulinichev
đã
phát
triển
hai
hệ
thống
đạo
trình
VCG
chưa
hiệu
chỉnh,một
ứng
dụng
có
5
mặt
hiển
thị
(Akulinichev,1956
)
và
một
ứng
dụng
khác
là
ba
mặt
hiển
thị
(Akulinichev,1960
).Trong
hệ
thống
5
mặt,cái
mà
ông
đề
xuất
năm
1951,các
điện
cực
được
đặt
trong
các
góc
của
một
hình
chóp
đề
bốn
điện
cực
ở
trên
mặt
trước
của
ngực
và
điện
cực
thứ
5
ở
đằng
sau,phía
trái
của
cột
sống
trên
mức
của
góc
dưới
của
xương
bả
vai.
Ivan
T.Alulinichev
đã
phát
triển
hai
hệ
thống
đạo
trình
VCG
chưa
hiệu
chỉnh,một
ứng
dụng
có
5
mặt
hiển
thị
(Akulinichev,1956
)
và
một
ứng
dụng
khác
là
ba
mặt
hiển
thị
(Akulinichev,1960
).Trong
hệ
thống
5
mặt,cái
mà
ông
đề
xuất
năm
1951,các
điện
cực
được
đặt
trong
các
góc
của
một
hình
chóp
đề
bốn
điện
cực
ở
trên
mặt
trước
của
ngực
và
điện
cực
thứ
5
ở
đằng
sau,phía
trái
của
cột
sống
trên
mức
của
góc
dưới
của
xương
bả
vai.
![]() Ở
hệ
thống
năm
Akulinichev
phép
chiếu
I
là
bề
mặt
phía
trước.Bốn
phép
chiếu
khác
được
xem
xét
sau
(Hình
16.6
A).Phép
chiếu
II
kiểm
tra
tâm
thất
trái
ở
một
dạng
hậu
nghiệm
cao
hơn
bên
trái.Phép
chiếu
III
và
IV
là
dạng
hậu
nghiệm
thấp
hơn
bên
phải
và
hậu
nghiệm
thấp
hơn
bên
trái,một
cách
tương
ứng.Phép
chiếu
V
kiểm
tra
tâm
nhĩ
trong
một
dạng
hậu
nghiệm
trên
hơn
bên
phải.Chú
ý
rằng
ở
bề
mặt
phía
trước
của
phép
đo
giữa
điện
cực
1
và
3
được
định
hướng
khoảng
dọc
trục
chính
của
tim.Năm
phép
chiếu
của
việc
ghi
vecto
điện
tim
đồ
với
hệ
thống
Akulinichev
được
hiển
thị
ở
Hình
16.6B.Bởi
vì
hai
phép
chiếu
là
cần
thiết
và
đầy
đủ
cho
việc
hiển
thị
một
không
gian
vecto
vòng.Hệ
thống
năm
mặt
Akulinichev
cung
cấp
nhiều
chi
tiết
thừa
hơn
so
với
những
hệ
thông
với
ba
phép
chiếu.
Ở
hệ
thống
năm
Akulinichev
phép
chiếu
I
là
bề
mặt
phía
trước.Bốn
phép
chiếu
khác
được
xem
xét
sau
(Hình
16.6
A).Phép
chiếu
II
kiểm
tra
tâm
thất
trái
ở
một
dạng
hậu
nghiệm
cao
hơn
bên
trái.Phép
chiếu
III
và
IV
là
dạng
hậu
nghiệm
thấp
hơn
bên
phải
và
hậu
nghiệm
thấp
hơn
bên
trái,một
cách
tương
ứng.Phép
chiếu
V
kiểm
tra
tâm
nhĩ
trong
một
dạng
hậu
nghiệm
trên
hơn
bên
phải.Chú
ý
rằng
ở
bề
mặt
phía
trước
của
phép
đo
giữa
điện
cực
1
và
3
được
định
hướng
khoảng
dọc
trục
chính
của
tim.Năm
phép
chiếu
của
việc
ghi
vecto
điện
tim
đồ
với
hệ
thống
Akulinichev
được
hiển
thị
ở
Hình
16.6B.Bởi
vì
hai
phép
chiếu
là
cần
thiết
và
đầy
đủ
cho
việc
hiển
thị
một
không
gian
vecto
vòng.Hệ
thống
năm
mặt
Akulinichev
cung
cấp
nhiều
chi
tiết
thừa
hơn
so
với
những
hệ
thông
với
ba
phép
chiếu.
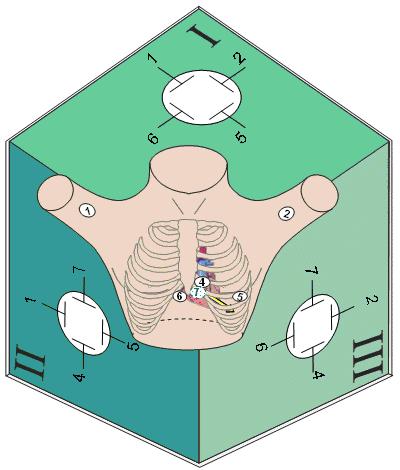
![]() Từ
hệ
thống
VCG
năm
mặt,Akulinichev
đã
phát
triển
sau
thành
hệ
thống
VCG
ba
mặt
(Akulinichev
,1960;Pawlow,1966;Wenger
,1969
).Một
chi
tiết
của
hệ
thống
đạo
trình
này
là
trục
trực
giao
chính
của
hệ
thống
được
định
hướng
dọc
theo
trục
chính
của
tim.Các
vị
trí
chính
xác
của
các
điện
cực
là
(xem
Hình
16.7
)
như
sau:1-tay
phải,2-tay
trái,4-V2,5-V5,6-mặt
phải
của
ức
mũi,7-V9
(trên
bề
mặt
hậu
nghiệm
của
của
ngực,tại
mặt
trái
của
cột
sống
ở
mức
trên
V4
và
V5
)Ba
đề
án
được
định
dạng
như
sau :phép
chiếu
I
=
các
điện
cực
1,2,5
và
6
(nghĩa
là
bề
mặt
phía
trước
);phép
chiếu
II=
các
điện
cức
1,7,5
và
4
nghĩa
là,song
song
với
trục
dọc
của
tim
);
phép
chiếu
III
=
các
điện
cực
6
,7,2
và
4
(
nghĩa
là,mặt
phẳng
pha
tạp
các
đoạn
của
tim
)
Từ
hệ
thống
VCG
năm
mặt,Akulinichev
đã
phát
triển
sau
thành
hệ
thống
VCG
ba
mặt
(Akulinichev
,1960;Pawlow,1966;Wenger
,1969
).Một
chi
tiết
của
hệ
thống
đạo
trình
này
là
trục
trực
giao
chính
của
hệ
thống
được
định
hướng
dọc
theo
trục
chính
của
tim.Các
vị
trí
chính
xác
của
các
điện
cực
là
(xem
Hình
16.7
)
như
sau:1-tay
phải,2-tay
trái,4-V2,5-V5,6-mặt
phải
của
ức
mũi,7-V9
(trên
bề
mặt
hậu
nghiệm
của
của
ngực,tại
mặt
trái
của
cột
sống
ở
mức
trên
V4
và
V5
)Ba
đề
án
được
định
dạng
như
sau :phép
chiếu
I
=
các
điện
cực
1,2,5
và
6
(nghĩa
là
bề
mặt
phía
trước
);phép
chiếu
II=
các
điện
cức
1,7,5
và
4
nghĩa
là,song
song
với
trục
dọc
của
tim
);
phép
chiếu
III
=
các
điện
cực
6
,7,2
và
4
(
nghĩa
là,mặt
phẳng
pha
tạp
các
đoạn
của
tim
)
![]() Các
hệ
thống
đạo
trình
Akulinichev
đã
được
áp
dụng
ở
Liên
Xô
cũ
và
Bulgari
kể
từ
năm
1960
và
thưc
tế
chỉ
hệ
thống
đạo
trình
điện
tâm
đồ
vecto
lâm
sàng
sử
dụng
nó
đến
ngày
nay.
Các
hệ
thống
đạo
trình
Akulinichev
đã
được
áp
dụng
ở
Liên
Xô
cũ
và
Bulgari
kể
từ
năm
1960
và
thưc
tế
chỉ
hệ
thống
đạo
trình
điện
tâm
đồ
vecto
lâm
sàng
sử
dụng
nó
đến
ngày
nay.
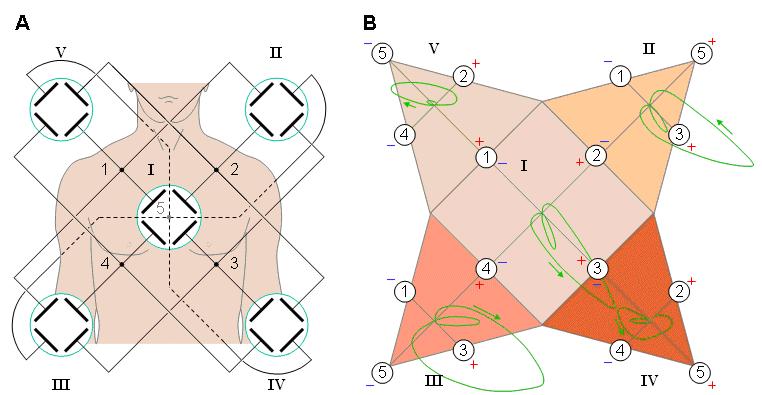
![]() (A)
Vị
trí
của
các
điện
cực
ở
trên
ngực
và
năm
đường
kết
nối
chúng
đến
máy
hiện
sóng
oscillo
(A)
Vị
trí
của
các
điện
cực
ở
trên
ngực
và
năm
đường
kết
nối
chúng
đến
máy
hiện
sóng
oscillo
![]() (B)
Năm
phép
chiếu
của
điện
tâm
đồ
(B)
Năm
phép
chiếu
của
điện
tâm
đồ
16.3 Hệ thống đạo trình điện tâm đồ vecto đã hiệu chỉnh
16.3.1 Hệ thống đạo trình Frank
ĐIỀU KIỆN ĐẦU :
NGUỒN:lưỡng cực ở vị trí cố định
VẬT DẪN:Xác định,đồng nhất
![]() Vào
năm
1956
Ernest
Frank
(Frank
,1956)
đã
giới
thiệu
một
hệ
thống
đạo
trình
các
vecto
dựa
trên
những
dữ
liệu
được
đưa
ra
trước
đây
của
bề
mặt
tưởng
tượng
(Frank
,1954).Do
bề
mặt
tưởng
tượng
đã
được
một
cho
một
việc
xác
định,mô
hình
lồng
ngực
đồng
nhất,mô
hình
vật
dẫn
khối
cho
hệ
thống
VCG
các
đạo
trình
Frank
cũng
giống
như
vậy.Trong
phần
sau,chúng
ta
bắt
đầu
thảo
luận
về
nguyên
tắc
thiết
kế
của
hệ
thống
các
đạo
trình
Frank.Sau
đó
chúng
ta
thảo
luận
về
việc
xây
dựng
của
các
thành
phần
trực
giao
lấn
nhau
và
hệ
thống
đo
lường.Mắc
dù
chúng
ta
tham
khảo
tại
đây
đề
công
bố
bản
gốc
của
Frank,chúng
ta
sử
dụng
hệ
thống
phối
hợp
trực
giao
được
diễn
tả
trong
phần
Phụ
lục.
Vào
năm
1956
Ernest
Frank
(Frank
,1956)
đã
giới
thiệu
một
hệ
thống
đạo
trình
các
vecto
dựa
trên
những
dữ
liệu
được
đưa
ra
trước
đây
của
bề
mặt
tưởng
tượng
(Frank
,1954).Do
bề
mặt
tưởng
tượng
đã
được
một
cho
một
việc
xác
định,mô
hình
lồng
ngực
đồng
nhất,mô
hình
vật
dẫn
khối
cho
hệ
thống
VCG
các
đạo
trình
Frank
cũng
giống
như
vậy.Trong
phần
sau,chúng
ta
bắt
đầu
thảo
luận
về
nguyên
tắc
thiết
kế
của
hệ
thống
các
đạo
trình
Frank.Sau
đó
chúng
ta
thảo
luận
về
việc
xây
dựng
của
các
thành
phần
trực
giao
lấn
nhau
và
hệ
thống
đo
lường.Mắc
dù
chúng
ta
tham
khảo
tại
đây
đề
công
bố
bản
gốc
của
Frank,chúng
ta
sử
dụng
hệ
thống
phối
hợp
trực
giao
được
diễn
tả
trong
phần
Phụ
lục.
Vị trí điện cực yêu cầu
![]() Để
đo
ba
thành
phần
lưỡng
cực,ít
nhất
là
bốn
điện
cực
(một
trong
những
tài
liệu
tham
khảo
)
là
cần
thiết.Frandk
đã
quyết
định
tăng
số
lượng
của
điện
cực
lên
thành
bảy,để
giảm
lỗi
do
sự
biến
thiên
của
những
cá
thể
riêng
lẻ
về
vị
trí
của
tim
và
hình
dạng
cơ
thể.
Để
đo
ba
thành
phần
lưỡng
cực,ít
nhất
là
bốn
điện
cực
(một
trong
những
tài
liệu
tham
khảo
)
là
cần
thiết.Frandk
đã
quyết
định
tăng
số
lượng
của
điện
cực
lên
thành
bảy,để
giảm
lỗi
do
sự
biến
thiên
của
những
cá
thể
riêng
lẻ
về
vị
trí
của
tim
và
hình
dạng
cơ
thể.
![]() Nó
là
quan
trọng
để
vị
trí
các
điện
cực
có
thể
dẽ
dàng
tìm
thấy
để
tăng
khả
năng
lặp
lại
của
việc
đo
lường.Khả
năng
lặp
lại
của
những
điện
cực
chân
tay
là
rất
tốt.Tuy
nhiên,điện
cực
tay
có
vấn
đề
đó
là
trường
đạo
trình
thay
đổi
đáng
kể
nếu
bệnh
nhân
chạm
đến
tay
đối
diện,bởi
vì
dòng
điện
chảy
qua
lớp
da
ướt
một
cách
trực
tiếp
đến
ngực.Vấn
đề
này
có
một
tầm
quan
trọng
đặc
biệt
đến
cánh
tay
trái,vì
rằng
nó
gần
tim
hơn.
Nó
là
quan
trọng
để
vị
trí
các
điện
cực
có
thể
dẽ
dàng
tìm
thấy
để
tăng
khả
năng
lặp
lại
của
việc
đo
lường.Khả
năng
lặp
lại
của
những
điện
cực
chân
tay
là
rất
tốt.Tuy
nhiên,điện
cực
tay
có
vấn
đề
đó
là
trường
đạo
trình
thay
đổi
đáng
kể
nếu
bệnh
nhân
chạm
đến
tay
đối
diện,bởi
vì
dòng
điện
chảy
qua
lớp
da
ướt
một
cách
trực
tiếp
đến
ngực.Vấn
đề
này
có
một
tầm
quan
trọng
đặc
biệt
đến
cánh
tay
trái,vì
rằng
nó
gần
tim
hơn.
Xác định vị trí các điện cực
![]() Dựa
trên
các
yêu
cầu
nêu
trên
Frank
đã
phát
mình
ra
một
hệ
thống
đạo
trình,bây
giớ
mang
tên
ông,trong
đó
cung
cấp
những
đạo
trình
trực
giao
đã
hiệu
chỉnh.Số
và
vị
trí
các
điện
cực
được
chon
rất
có
ý
đồ,và
dựa
trên
cơ
sở
mô
hình
bề
mặt
ảnh
của
ông
(xem
Hình
11.14
).Ông
đã
chọn
cấp
độ
6
cho
việc
đặt
các
điện
cưc,bởi
vì
vecto
đạo
trình
là
lớn
nhất
ở
cấp
độ
này.Một
cách
cụ
thể,ông
đã
chọn
các
điểm
được
kí
hiệu
là
A,E,I,và
M
tương
ứng
với
trái,phải,trước
và
sau.Ông
cũng
đã
chọn
điểm
C
giữa
A
và
E
bởi
vì
nó
gần
tim.Ngoài
ra,còn
bao
gồm
một
điểm
trên
cổ
và
một
điểm
ở
chân
trái.
Dựa
trên
các
yêu
cầu
nêu
trên
Frank
đã
phát
mình
ra
một
hệ
thống
đạo
trình,bây
giớ
mang
tên
ông,trong
đó
cung
cấp
những
đạo
trình
trực
giao
đã
hiệu
chỉnh.Số
và
vị
trí
các
điện
cực
được
chon
rất
có
ý
đồ,và
dựa
trên
cơ
sở
mô
hình
bề
mặt
ảnh
của
ông
(xem
Hình
11.14
).Ông
đã
chọn
cấp
độ
6
cho
việc
đặt
các
điện
cưc,bởi
vì
vecto
đạo
trình
là
lớn
nhất
ở
cấp
độ
này.Một
cách
cụ
thể,ông
đã
chọn
các
điểm
được
kí
hiệu
là
A,E,I,và
M
tương
ứng
với
trái,phải,trước
và
sau.Ông
cũng
đã
chọn
điểm
C
giữa
A
và
E
bởi
vì
nó
gần
tim.Ngoài
ra,còn
bao
gồm
một
điểm
trên
cổ
và
một
điểm
ở
chân
trái.
Thành phần từ phải qua trái (thành phần y)
![]() Chúng
ta
bắt
đầu
với
thành
phần
từ
phải
qua
trái
(
thành
phần
y
)
bới
vì
cấu
trúc
của
nó
là
đơn
giản
nhất
và
dễ
hiểu.Vecto
đạo
trình
trong
hướng
này
được
xác
định
bởi
việc
áp
dụng
các
phương
pháp
đã
được
đề
cập
trước
đó
trong
Hình
16.8.Hình
này
cho
thấy
hình
vẽ
giải
phẫu
ở
cấp
độ
6
cũng
tốt
như
bề
mặt
ảnh
được
đo
bởi
Frank.Vị
trí
không
gian
ảnh
của
các
điện
cực
A,C
va
I
cũng
chỉ
ra
từ
việc
đã
được
chọn
để
nhận
ra
thành
phần
y
của
điện
tâm
đồ
vecto.
Chúng
ta
bắt
đầu
với
thành
phần
từ
phải
qua
trái
(
thành
phần
y
)
bới
vì
cấu
trúc
của
nó
là
đơn
giản
nhất
và
dễ
hiểu.Vecto
đạo
trình
trong
hướng
này
được
xác
định
bởi
việc
áp
dụng
các
phương
pháp
đã
được
đề
cập
trước
đó
trong
Hình
16.8.Hình
này
cho
thấy
hình
vẽ
giải
phẫu
ở
cấp
độ
6
cũng
tốt
như
bề
mặt
ảnh
được
đo
bởi
Frank.Vị
trí
không
gian
ảnh
của
các
điện
cực
A,C
va
I
cũng
chỉ
ra
từ
việc
đã
được
chọn
để
nhận
ra
thành
phần
y
của
điện
tâm
đồ
vecto.
![]() Nguyên
tắc
cơ
bản
trong
việc
thiết
kế
thành
phần
y
của
hệ
thống
đạo
trình
là
tổng
hợp
không
gian
ảnh,với
việc
xuất
hiện
các
điểm
điệc
cực,một
vecto
đạo
trình
được
định
hướng
theo
hướng
y.Đây
chỉ
là
yêu
câu
phải
được
hoàn
thành
cho
đạo
trình
để
ghi
lại
thành
phần
y.
Nguyên
tắc
cơ
bản
trong
việc
thiết
kế
thành
phần
y
của
hệ
thống
đạo
trình
là
tổng
hợp
không
gian
ảnh,với
việc
xuất
hiện
các
điểm
điệc
cực,một
vecto
đạo
trình
được
định
hướng
theo
hướng
y.Đây
chỉ
là
yêu
câu
phải
được
hoàn
thành
cho
đạo
trình
để
ghi
lại
thành
phần
y.
![]() Ngoài
ra,đó
là
thuận
lợi
để
lựa
chọn
trong
số
tất
cả
những
vecto
đạo
trình
theo
hướng
y
một
cái
là
lớn
nhất.Điều
này
đảm
bảo
tỷ
lệ
tín
hiệu-
nhiễu
là
càng
cao
càng
tốt.
Ngoài
ra,đó
là
thuận
lợi
để
lựa
chọn
trong
số
tất
cả
những
vecto
đạo
trình
theo
hướng
y
một
cái
là
lớn
nhất.Điều
này
đảm
bảo
tỷ
lệ
tín
hiệu-
nhiễu
là
càng
cao
càng
tốt.
![]() Nếu
chúng
ta
thiết
kế
không
gian
ảnh
điểm
I’
là
một
trong
những
điểm
vecto
đạo
trình
được
chọn
song
song
với
trục
y,các
điểm
kết
thúc
khác
được
tìm
thấy
trên
đường
A’-C’,và
được
đặt
tên
là
a’.Điểm
a’
chia
A’-C’
theo
tỉ
lệ
1:3,59.Bằng
việc
kết
nối
hai
điện
trở
có
giá
trị
theo
tỉ
lệ
này
giữa
các
điểm
A
và
C
trong
không
gian
thực,điểm
a
được
nhận
ra
tại
các
giao
điểm.
Nếu
chúng
ta
thiết
kế
không
gian
ảnh
điểm
I’
là
một
trong
những
điểm
vecto
đạo
trình
được
chọn
song
song
với
trục
y,các
điểm
kết
thúc
khác
được
tìm
thấy
trên
đường
A’-C’,và
được
đặt
tên
là
a’.Điểm
a’
chia
A’-C’
theo
tỉ
lệ
1:3,59.Bằng
việc
kết
nối
hai
điện
trở
có
giá
trị
theo
tỉ
lệ
này
giữa
các
điểm
A
và
C
trong
không
gian
thực,điểm
a
được
nhận
ra
tại
các
giao
điểm.
![]() Từ
một
điểm
thực
tế
của
việc
quan
sát
đó
là
quan
trọng
để
khuyếch
đại
trở
kháng
thấy
trong
mỗi
đạo
trình
là
bình
đẳng.Một
sự
cân
bằng
tốt
đảm
bảo
việc
hủy
bỏ
chế
độ
phổ
biến
tín
hiệu
nhiễu.Nếu
chúng
ta
thiết
kế
trở
kháng
này
như
R,chúng
ta
phải
thêm
vào
một
điện
trở
đến
đạo
trình
ở
điện
cực
I
và
nhân
các
điện
trở
song
song
của
đạo
trình
A
và
C
bởi
các
yếu
tố
1.28.Điều
này
mang
lại
giá
trị
điện
trở
là
1.28R
và
4.59R,một
cách
tương
ứng.(Chú
ý
rằng
bây
giớ
trở
kháng
song
song
của
hai
điện
trở
đó
là
R
).Từ
một
việc
đo
lường
trong
không
gian
ảnh
chúng
ta
xác
định
độ
dài
của
vecto
đạo
trình
y
là
174
đơn
vị
liên
quan...
Từ
một
điểm
thực
tế
của
việc
quan
sát
đó
là
quan
trọng
để
khuyếch
đại
trở
kháng
thấy
trong
mỗi
đạo
trình
là
bình
đẳng.Một
sự
cân
bằng
tốt
đảm
bảo
việc
hủy
bỏ
chế
độ
phổ
biến
tín
hiệu
nhiễu.Nếu
chúng
ta
thiết
kế
trở
kháng
này
như
R,chúng
ta
phải
thêm
vào
một
điện
trở
đến
đạo
trình
ở
điện
cực
I
và
nhân
các
điện
trở
song
song
của
đạo
trình
A
và
C
bởi
các
yếu
tố
1.28.Điều
này
mang
lại
giá
trị
điện
trở
là
1.28R
và
4.59R,một
cách
tương
ứng.(Chú
ý
rằng
bây
giớ
trở
kháng
song
song
của
hai
điện
trở
đó
là
R
).Từ
một
việc
đo
lường
trong
không
gian
ảnh
chúng
ta
xác
định
độ
dài
của
vecto
đạo
trình
y
là
174
đơn
vị
liên
quan...
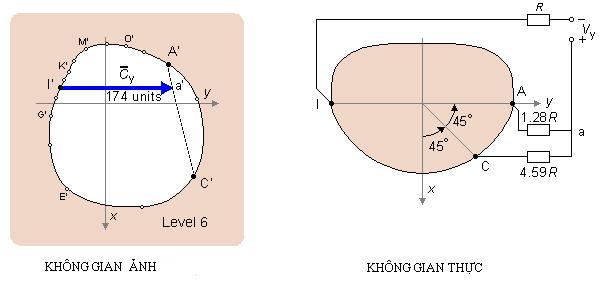
Hình 16.8 Xác định thành phần từ phải quá trái (thành phần y) trong hệ thống đạo trình Frank.Không gian ảnh hiển thị bên trái tương ứng với mặt phẳng nằm ngang thực tế bên phải.
Thành phần từ chân tới đầu (thành phần z )
![]() Từ
những
không
gian
ảnh
trong
Hình
16.9,chúng
ta
có
thể
xác
định
rằng
nếu
chúng
ta
chọn
một
điểm
cuối
của
hình
ảnh
vecto
điểm
H’
trong
cấp
độ
1
(tức
là
trên
cổ
),ở
đó
tồn
tại
một
điểm
k’
trên
đường
F’-M’
,như
vậy
K’-H’
tạo
thành
một
vecto
đạo
trình
song
song
với
truc
z.Điểm
k’
chia
trục
theo
tỉ
lệ
1:1.9.Một
lần
nữa
đạo
trình
được
cân
bằng
bởi
đặt
một
điện
trở
R
vào
trong
điện
cực
F
và
M
bởi
một
yêu
cầu
1.53
có
giá
trị
tương
ứng
là
1.53R
và
2.90R.Chiều
dài
của
vecto
đạo
trình
z
là
136
đơn
vị.
Từ
những
không
gian
ảnh
trong
Hình
16.9,chúng
ta
có
thể
xác
định
rằng
nếu
chúng
ta
chọn
một
điểm
cuối
của
hình
ảnh
vecto
điểm
H’
trong
cấp
độ
1
(tức
là
trên
cổ
),ở
đó
tồn
tại
một
điểm
k’
trên
đường
F’-M’
,như
vậy
K’-H’
tạo
thành
một
vecto
đạo
trình
song
song
với
truc
z.Điểm
k’
chia
trục
theo
tỉ
lệ
1:1.9.Một
lần
nữa
đạo
trình
được
cân
bằng
bởi
đặt
một
điện
trở
R
vào
trong
điện
cực
F
và
M
bởi
một
yêu
cầu
1.53
có
giá
trị
tương
ứng
là
1.53R
và
2.90R.Chiều
dài
của
vecto
đạo
trình
z
là
136
đơn
vị.
Thành phần từ mặt sau ra mặt trước (thành phần x)
![]() Trong
thiết
kế
của
thành
phần
x
mà
Frank
mong
muốn,thêm
vào
những
yêu
cầu
trước,chọn
lựa
một
trọng
số
cho
các
điện
cực
để
sự
biến
thiên
các
vecto
đạo
trình
trong
toàn
bộ
tim
sẽ
được
thống
nhất
khi
có
thể.Do
đó,Frank
sử
dụng
toàn
bộ
năm
điện
cực
ở
cấp
độ
6.Mặt
phẳng
chiếu
nằm
ngang
của
bề
mặt
ảnh
được
hiển
thị
lần
nữa
ở
Hình
16.10,và
các
điện
cực
A,C,E,I
và
M
được
mô
rất
trong
cả
không
gian
thực
và
không
gian
ảnh.
Trong
thiết
kế
của
thành
phần
x
mà
Frank
mong
muốn,thêm
vào
những
yêu
cầu
trước,chọn
lựa
một
trọng
số
cho
các
điện
cực
để
sự
biến
thiên
các
vecto
đạo
trình
trong
toàn
bộ
tim
sẽ
được
thống
nhất
khi
có
thể.Do
đó,Frank
sử
dụng
toàn
bộ
năm
điện
cực
ở
cấp
độ
6.Mặt
phẳng
chiếu
nằm
ngang
của
bề
mặt
ảnh
được
hiển
thị
lần
nữa
ở
Hình
16.10,và
các
điện
cực
A,C,E,I
và
M
được
mô
rất
trong
cả
không
gian
thực
và
không
gian
ảnh.
![]() Frank
đã
vẽ
các
đường
A’-M’
,E’-C’
và
g’-I’
trong
không
gian
ảnh,từ
đó
các
điểm
g’
đã
được
nằm
trên
E’-C’.Giữa
các
đường
A’-M’
và
g’-I’
ông
đã
vẽ
một
đoạn
f’-h’
song
song
với
trục
x.Đây
là
vecto
đạo
trình
tương
ứng
với
đạo
trình
x
và
đáp
ứng
đầy
đủ
các
yêu
cầu
đã
thảo
luận
ở
trên.
Frank
đã
vẽ
các
đường
A’-M’
,E’-C’
và
g’-I’
trong
không
gian
ảnh,từ
đó
các
điểm
g’
đã
được
nằm
trên
E’-C’.Giữa
các
đường
A’-M’
và
g’-I’
ông
đã
vẽ
một
đoạn
f’-h’
song
song
với
trục
x.Đây
là
vecto
đạo
trình
tương
ứng
với
đạo
trình
x
và
đáp
ứng
đầy
đủ
các
yêu
cầu
đã
thảo
luận
ở
trên.
![]() Bản
chất
vật
lý
của
các
đạo
trình
tương
ứng
với
sự
chọn
lựa
vecto
đạo
trình
được
tìm
kiếm
như
sau:Từ
không
gian
ảnh,nó
có
thể
thiết
lập
điểm
f’
chia
đoạn
trên
đường
A’-M’
theo
tỉ
lệ
5.56:1.Nhân
chúng
với
1.18,chúng
ta
có
được
các
giá
trị
6.56:1.18
có
một
trở
kháng
song
song
giá
trị
1.Bằng
sự
kết
nối
giữa
hai
điện
trở
và
tỉ
lệ
tương
tự
trong
dãy,giữa
điện
cực
A
và
M,chúng
ta
thấy
rằng
các
điểm
của
chúng
của
việc
kết
nối
ở
không
gian
thực
là
f.
Bản
chất
vật
lý
của
các
đạo
trình
tương
ứng
với
sự
chọn
lựa
vecto
đạo
trình
được
tìm
kiếm
như
sau:Từ
không
gian
ảnh,nó
có
thể
thiết
lập
điểm
f’
chia
đoạn
trên
đường
A’-M’
theo
tỉ
lệ
5.56:1.Nhân
chúng
với
1.18,chúng
ta
có
được
các
giá
trị
6.56:1.18
có
một
trở
kháng
song
song
giá
trị
1.Bằng
sự
kết
nối
giữa
hai
điện
trở
và
tỉ
lệ
tương
tự
trong
dãy,giữa
điện
cực
A
và
M,chúng
ta
thấy
rằng
các
điểm
của
chúng
của
việc
kết
nối
ở
không
gian
thực
là
f.
![]() Tương
tự
như
điểm
g’
chia
đoạn
không
gian
ảnh
của
đường
C’-E’
theo
tỉ
lệ
1.61:1.Giá
trị
song
song
của
chúng
là
0.62.Điểm
h’
chia
đoạn
của
đường
g’-I’
theo
tỉ
lệ
1:2.29.Nếu
chúng
nhân
với
0.62,chúng
ta
thu
được
0.62:1.14.Bây
giờ
chúng
ta
có
quan
hệ
các
giá
trị
điện
trở
1.61,1,
và
1.41
tương
ứng
với
các
điện
cực
C,E
và
I.Để
điều
chỉnh
trở
kháng
song
song
đều
bằng
1,chúng
ta
nhân
tứng
giá
trị
với
2.32
và
chũng
ta
thu
được
3.74R
,2.32R
và
3.72R.Bây
giờ
chúng
ta
có
thể
tổng
hợp
vecto
đạo
trình
Cx;liên
quan
đến
các
giả
định
về
quy
mô
không
gian
ảnh,nó
có
độ
lớn
là
156
đơn
vị…
Tương
tự
như
điểm
g’
chia
đoạn
không
gian
ảnh
của
đường
C’-E’
theo
tỉ
lệ
1.61:1.Giá
trị
song
song
của
chúng
là
0.62.Điểm
h’
chia
đoạn
của
đường
g’-I’
theo
tỉ
lệ
1:2.29.Nếu
chúng
nhân
với
0.62,chúng
ta
thu
được
0.62:1.14.Bây
giờ
chúng
ta
có
quan
hệ
các
giá
trị
điện
trở
1.61,1,
và
1.41
tương
ứng
với
các
điện
cực
C,E
và
I.Để
điều
chỉnh
trở
kháng
song
song
đều
bằng
1,chúng
ta
nhân
tứng
giá
trị
với
2.32
và
chũng
ta
thu
được
3.74R
,2.32R
và
3.72R.Bây
giờ
chúng
ta
có
thể
tổng
hợp
vecto
đạo
trình
Cx;liên
quan
đến
các
giả
định
về
quy
mô
không
gian
ảnh,nó
có
độ
lớn
là
156
đơn
vị…
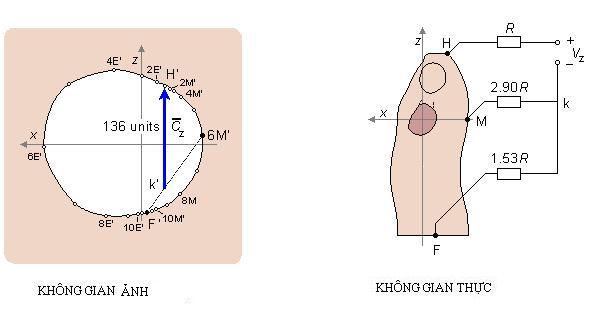
Hình 16.9 Xác định thành phần chân tới đầu (thành phần z ) trong hệ thống đạo trình Frank.Không gian ảnh được hiển thị ở bên trái tương ứng với mặt giữa thực tế ở bên phải.
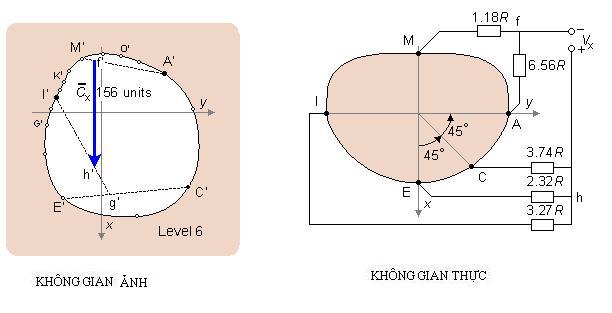
Hình 16.10 Xác đinh thành phần từ mặt sau ra mặt trước (thành phần x ) trong hệ thống đạo trình Frank.Không gian ảnh hiển thị ở bên trái tương ứng với mặt ngang thực tế ở bên phải.
Ma trận các đạo trình Frank
![]() Ngay
bây
giờ
chúng
ta
có
thể
xác
định
được
tất
cả
ba
vecto
đạo
trình
cái
mà
ở
dạng
một
hệ
thống
đạo
trình
trực
giao.Hệ
thống
này
vấn
phải
được
chuẩn
hóa.Vì
vậy,điện
trở
13.3R
và
7.15R
được
nối
giữa
các
đạo
trình
của
thành
phẩn
x
và
y
để
làm
giảm
những
tín
hiệu
đó
để
có
cùng
cấp
độ
như
tín
hiệu
đạo
trình
z.Bây
giờ
hệ
thống
đạo
trình
Frank
là
trực
giao.
Ngay
bây
giờ
chúng
ta
có
thể
xác
định
được
tất
cả
ba
vecto
đạo
trình
cái
mà
ở
dạng
một
hệ
thống
đạo
trình
trực
giao.Hệ
thống
này
vấn
phải
được
chuẩn
hóa.Vì
vậy,điện
trở
13.3R
và
7.15R
được
nối
giữa
các
đạo
trình
của
thành
phẩn
x
và
y
để
làm
giảm
những
tín
hiệu
đó
để
có
cùng
cấp
độ
như
tín
hiệu
đạo
trình
z.Bây
giờ
hệ
thống
đạo
trình
Frank
là
trực
giao.
![]() Cần
lưu
ý
một
lần
nữa
rằng
trở
kháng
của
mạng
điện
trở
đã
kết
nối
mỗi
cặp
đạo
trình
là
duy
nhất.Kết
quả
lựa
chọn
này
trong
sự
cân
bằng
tải
và
tăng
độ
chọn
lọc
chế
độ
phổ
biến
của
hệ
thống.Giá
trị
tuyệt
đối
của
R
là
được
xác
định.Đối
với
yếu
tố
này
Frank
khuyến
cáo
rằng
nên
có
ít
nhất
là
25
kΩ
và
tốt
nhất
là
100
kΩ.Ngày
nay
tín
hiệu
đạo
trình
thường
được
phát
hiện
với
một
tiền
khuyếch
đại
trở
kháng
cao,và
hàm
ma
trận
đạo
trình
được
thực
hiện
bởi
một
khuyếch
đại
thuật
toán
hoặc
số
ngay
sau
đó.Hình
16.11
miêu
tả
ma
trận
đạo
trình
Frank
đầy
đủ.
Cần
lưu
ý
một
lần
nữa
rằng
trở
kháng
của
mạng
điện
trở
đã
kết
nối
mỗi
cặp
đạo
trình
là
duy
nhất.Kết
quả
lựa
chọn
này
trong
sự
cân
bằng
tải
và
tăng
độ
chọn
lọc
chế
độ
phổ
biến
của
hệ
thống.Giá
trị
tuyệt
đối
của
R
là
được
xác
định.Đối
với
yếu
tố
này
Frank
khuyến
cáo
rằng
nên
có
ít
nhất
là
25
kΩ
và
tốt
nhất
là
100
kΩ.Ngày
nay
tín
hiệu
đạo
trình
thường
được
phát
hiện
với
một
tiền
khuyếch
đại
trở
kháng
cao,và
hàm
ma
trận
đạo
trình
được
thực
hiện
bởi
một
khuyếch
đại
thuật
toán
hoặc
số
ngay
sau
đó.Hình
16.11
miêu
tả
ma
trận
đạo
trình
Frank
đầy
đủ.
![]() Rất
cần
được
nhắc
đến
rằng
Hệ
thống
Frank
ngày
nay
là
phổ
biến
nhất
trong
tất
cả
các
hệ
thông
VCG
lâm
sàng
trên
toàn
thế
giới.(
Ngoài
ra,VCG
tương
ứng
chiếm
ít
hơn
5%
của
điện
tim
đồ.).
Rất
cần
được
nhắc
đến
rằng
Hệ
thống
Frank
ngày
nay
là
phổ
biến
nhất
trong
tất
cả
các
hệ
thông
VCG
lâm
sàng
trên
toàn
thế
giới.(
Ngoài
ra,VCG
tương
ứng
chiếm
ít
hơn
5%
của
điện
tim
đồ.).
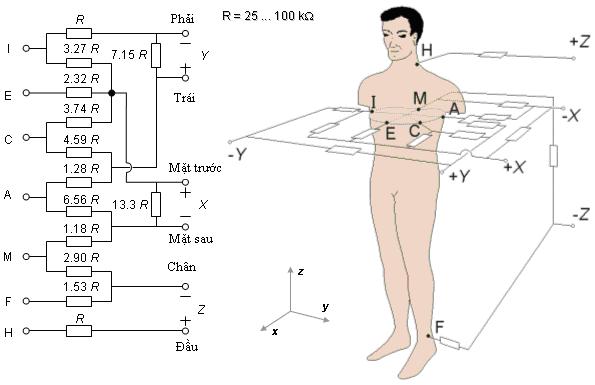
Hình 16.11 Ma trận đạo trình của hệ thống VCG Frank.Các điện cực được đánh dấu I,E,C,A,M,F và H, và vị trí thuộc về giải phẫu của chúng được hiển thị.Kết quả của ma trận điện trở với việc thiết lập của các thành phần vecto đạo trình đã chuẩn hóa x ,y và z,như được mô tả ở trên.
16.3.2 Hệ thống đạo trình McFee-Parungao
ĐIỀU KIỆN ĐẦU :
NGUỒN:momen lưỡng cực của một nguồn khối.
VẬT DẪN :Xác định,đồng nhất
![]() McFee
và
Parungao
(1961)
công
bố
một
hệ
thống
VCG
các
đạo
trình
đơn
giản
được
gọi
là
hệ
thống
hướng
tâm,dựa
trên
một
phương
pháp
tiếp
cận
lý
thuyết
trường
đạo
trình.Ngoài
ra,tim
được
mô
hình
hóa
với
một
nguồn
khối
và
ngực
được
giả
định
là
đồng
nhất.
McFee
và
Parungao
(1961)
công
bố
một
hệ
thống
VCG
các
đạo
trình
đơn
giản
được
gọi
là
hệ
thống
hướng
tâm,dựa
trên
một
phương
pháp
tiếp
cận
lý
thuyết
trường
đạo
trình.Ngoài
ra,tim
được
mô
hình
hóa
với
một
nguồn
khối
và
ngực
được
giả
định
là
đồng
nhất.
![]() Ba
trường
đạo
trình
thống
nhất
được
thiết
kế
theo
các
nguyên
tắc
đã
thảo
luận
trong
Phần
11.6.10.Để
phát
hiện
ra
ba
thành
phần
trực
giao
của
điện
tim
đồ,ba
cặp
của
(đơn
hoặc
đa
)
các
điện
cực
phải
được
sủ
dụng
trên
mỗi
trục
trực
giao,một
trong
cả
hai
mặt
của
tim.McFee
và
Parungao
công
nhận
để
gắn
kết
giữa
trái
tim
và
các
điện
cực
thì
việc
đặt
thêm
các
điện
cực
phải
sử
dụng
để
đạt
được
trường
đạo
trình
đồng
nhất
trong
khu
vực
của
tim.
Ba
trường
đạo
trình
thống
nhất
được
thiết
kế
theo
các
nguyên
tắc
đã
thảo
luận
trong
Phần
11.6.10.Để
phát
hiện
ra
ba
thành
phần
trực
giao
của
điện
tim
đồ,ba
cặp
của
(đơn
hoặc
đa
)
các
điện
cực
phải
được
sủ
dụng
trên
mỗi
trục
trực
giao,một
trong
cả
hai
mặt
của
tim.McFee
và
Parungao
công
nhận
để
gắn
kết
giữa
trái
tim
và
các
điện
cực
thì
việc
đặt
thêm
các
điện
cực
phải
sử
dụng
để
đạt
được
trường
đạo
trình
đồng
nhất
trong
khu
vực
của
tim.
Thành phần từ mặt sau ra mặt trước (thành phần x )
![]() McFee
và
Parungao
cảm
thấy
rằng
ba
điện
cực
phía
trước
nên
được
cho
việc
đo
lường
thanh
phần
từ
phía
sau
đến
phía
trước
của
VCG.Điều
này
sẽ
tạo
ra
một
trương
đạo
trình
với
sự
đồng
nhất
đầy
đủ
thậm
chí
mặc
dù
tim
gần
với
mặt
trước
của
ngực.Họ
theo
dõi
phương
pháp
việc
tổng
hợp
ý
tưởng
về
trường
đạo
trình
như
đã
được
thảo
luận
ở
Phần
11.5.8.Bằng
sự
kết
nối
trở
kháng
100
kΩ
với
mỗi
điện
cực,trở
kháng
mạng
đạo
trình
là
33
kΩ.
McFee
và
Parungao
cảm
thấy
rằng
ba
điện
cực
phía
trước
nên
được
cho
việc
đo
lường
thanh
phần
từ
phía
sau
đến
phía
trước
của
VCG.Điều
này
sẽ
tạo
ra
một
trương
đạo
trình
với
sự
đồng
nhất
đầy
đủ
thậm
chí
mặc
dù
tim
gần
với
mặt
trước
của
ngực.Họ
theo
dõi
phương
pháp
việc
tổng
hợp
ý
tưởng
về
trường
đạo
trình
như
đã
được
thảo
luận
ở
Phần
11.5.8.Bằng
sự
kết
nối
trở
kháng
100
kΩ
với
mỗi
điện
cực,trở
kháng
mạng
đạo
trình
là
33
kΩ.
![]() Các
vị
trí
chính
xác
của
các
điện
cực
trên
ngực
được
tìm
như
sau:Các
điện
cực
đặt
trong
một
hình
tam
giác
đều
để
định
hướng
cho
nó
với
khoảng
ngắn
nhất
đến
chân.Các
điện
cực
có
khoảng
cách
6cm
từ
trung
tâm
của
tam
giác
đó.Trung
tâm
của
tam
giác
nằm
tại
vị
trí
của
không
gian
xương
sườn
thứ
5,lệch
2
cm
về
bên
trái
với
lề
của
xương
ức.Vị
trí
này
nên
đảm
bảo
rằng
các
điện
cực
trên
ngực
được
đặt
một
cách
trực
tiếp
trên
trọng
tâm
của
tâm
thất
(điều
này
được
mô
tả
ở
Hình
16.12
).
Các
vị
trí
chính
xác
của
các
điện
cực
trên
ngực
được
tìm
như
sau:Các
điện
cực
đặt
trong
một
hình
tam
giác
đều
để
định
hướng
cho
nó
với
khoảng
ngắn
nhất
đến
chân.Các
điện
cực
có
khoảng
cách
6cm
từ
trung
tâm
của
tam
giác
đó.Trung
tâm
của
tam
giác
nằm
tại
vị
trí
của
không
gian
xương
sườn
thứ
5,lệch
2
cm
về
bên
trái
với
lề
của
xương
ức.Vị
trí
này
nên
đảm
bảo
rằng
các
điện
cực
trên
ngực
được
đặt
một
cách
trực
tiếp
trên
trọng
tâm
của
tâm
thất
(điều
này
được
mô
tả
ở
Hình
16.12
).
![]() Do
mặt
phía
sau
của
ngực
có
khoảng
cách
lớn
hơn
đến
tim
,nên
chỉ
một
điện
cực
cần
thiết
được
đặt
tại
đó.Điện
cực
phía
sau
nằm
một
cách
trực
tiếp
phía
sau
trung
tâm
của
tam
giác
trên
ngực.McFee
và
Parungao
không
cân
bằng
hệ
thống
đạo
trình
chống
lại
chế
độ
tiếng
ồn
phổ
biến.Các
tác
giả
đề
nghị
rằng
nếu
một
điện
trở
33
kΩ
đã
được
kết
nối
với
điện
cực
phía
sau
,sự
cân
bằng
yêu
cầu,được
thảo
luận
trước,đã
được
hoàn
thành.
Do
mặt
phía
sau
của
ngực
có
khoảng
cách
lớn
hơn
đến
tim
,nên
chỉ
một
điện
cực
cần
thiết
được
đặt
tại
đó.Điện
cực
phía
sau
nằm
một
cách
trực
tiếp
phía
sau
trung
tâm
của
tam
giác
trên
ngực.McFee
và
Parungao
không
cân
bằng
hệ
thống
đạo
trình
chống
lại
chế
độ
tiếng
ồn
phổ
biến.Các
tác
giả
đề
nghị
rằng
nếu
một
điện
trở
33
kΩ
đã
được
kết
nối
với
điện
cực
phía
sau
,sự
cân
bằng
yêu
cầu,được
thảo
luận
trước,đã
được
hoàn
thành.
Thành phần phải qua trái ( thành phần y )
![]() Đối
với
thành
phần
y
cũng
giống
như
một
thủ
tục
được
mô
tả
ở
trên
đã
được
làm
theo.McFee
và
Parungao
đã
đặt
hai
điện
cực
với
điện
trở
66
kΩ
ở
phía
bên
trái
và
một
điện
cực
phía
bên
phải
của
ngực.Điện
cực
bên
phải
được
đặt
cùng
một
mức
giống
với
trung
tâm
của
điện
cực
tam
giác
trên
ngực.Nó
được
đặt
bên
phải,một
phần
ba
của
đường
từ
ngực
trở
về
sau.Các
điện
cực
ở
bên
trái
cũng
được
đặt
ở
một
phần
ba
của
đường
trở
về
sau
theo
chiều
dọc
ở
mức
5.5
cm
ở
trên
và
dưới
mức
độ
trung
tâm
của
tam
giác
trên
ngực.Các
điện
cực
do
đó
có
khoảng
cách
là
11cm.Những
điện
cực
đó
được
đặt
một
cách
hợp
lí
thống
nhất
trường
đạo
trình
từ
phải
sang
trái
trong
vùng
của
tim.
Đối
với
thành
phần
y
cũng
giống
như
một
thủ
tục
được
mô
tả
ở
trên
đã
được
làm
theo.McFee
và
Parungao
đã
đặt
hai
điện
cực
với
điện
trở
66
kΩ
ở
phía
bên
trái
và
một
điện
cực
phía
bên
phải
của
ngực.Điện
cực
bên
phải
được
đặt
cùng
một
mức
giống
với
trung
tâm
của
điện
cực
tam
giác
trên
ngực.Nó
được
đặt
bên
phải,một
phần
ba
của
đường
từ
ngực
trở
về
sau.Các
điện
cực
ở
bên
trái
cũng
được
đặt
ở
một
phần
ba
của
đường
trở
về
sau
theo
chiều
dọc
ở
mức
5.5
cm
ở
trên
và
dưới
mức
độ
trung
tâm
của
tam
giác
trên
ngực.Các
điện
cực
do
đó
có
khoảng
cách
là
11cm.Những
điện
cực
đó
được
đặt
một
cách
hợp
lí
thống
nhất
trường
đạo
trình
từ
phải
sang
trái
trong
vùng
của
tim.
![]() McFee
và
Parungao
cũng
không
cân
bằng
đạo
trình
y.Tác
giả
cho
rằng
việc
thêm
một
điện
trở
33
kΩ
vào
điện
cức
bên
phải
cân
bằng
đạo
trình
chống
lại
chế
độ
nhiễu
phổ
biến.
McFee
và
Parungao
cũng
không
cân
bằng
đạo
trình
y.Tác
giả
cho
rằng
việc
thêm
một
điện
trở
33
kΩ
vào
điện
cức
bên
phải
cân
bằng
đạo
trình
chống
lại
chế
độ
nhiễu
phổ
biến.
Thành phần từ chân tới đầu (thành phần z )
![]() Các
điện
cực
được
thiết
kế
để
đo
lường
thành
phần
z
của
VCG
là
rất
xa
so
với
tim
cái
mà
McFee
và
Parungao
chỉ
sử
dụng
một
điện
cực
trên
cổ
và
một
ở
chân
trái.Những
điện
cực
này
có
thể
được
trang
bị
với
điện
trở
33
kΩ
cho
hệ
thống
đạo
trình
nào
đã
được
cân
bằng.Hệ
thống
đạo
trình
VCG
đầy
đủ
McFee
và
Parungao
được
hiển
thị
ở
Hình
16.12
Các
điện
cực
được
thiết
kế
để
đo
lường
thành
phần
z
của
VCG
là
rất
xa
so
với
tim
cái
mà
McFee
và
Parungao
chỉ
sử
dụng
một
điện
cực
trên
cổ
và
một
ở
chân
trái.Những
điện
cực
này
có
thể
được
trang
bị
với
điện
trở
33
kΩ
cho
hệ
thống
đạo
trình
nào
đã
được
cân
bằng.Hệ
thống
đạo
trình
VCG
đầy
đủ
McFee
và
Parungao
được
hiển
thị
ở
Hình
16.12
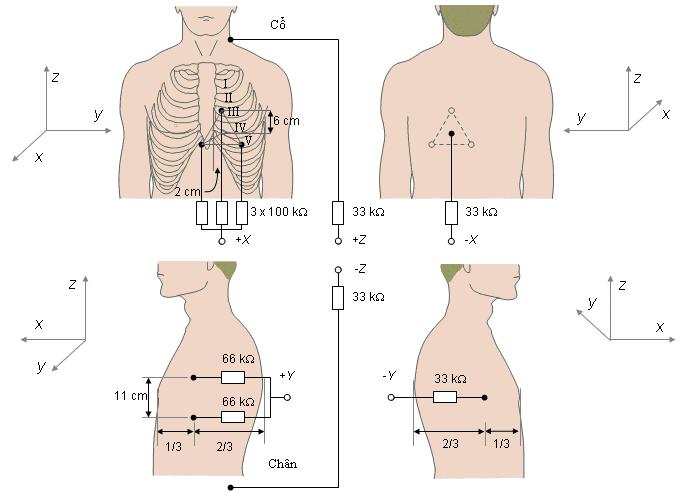
16.3.3 Hệ thống đạo trình SVEC III
ĐIỀU KIỆN ĐẦU :
NGUỒN :Momen lưỡng cực của một nguồn khối
VẬT DẪN :Xác định,đồng chất
![]() Otto
H.Schimitt
và
Ernst
Simonson
đã
phát
triển
nhiều
phiên
bản
của
hệ
thống
đạo
trình
điện
tâm
đồ
vecto,và
gọi
chúng
là
ghi
vecto
điện
tim
nổi
(stereovectorelectrocardiography
SVEC).Phiên
bản
thứ
ba,SVEC
III,được
công
bố
năm
1955
(Schmitt
và
Simonson,1955
).Nó
đòi
hỏi
tổng
ố
14
điện
cực
và
tạo
thành
một
trường
đạo
trình
trên
ngực
cái
mà
rất
đối
xứng
với
mặt
phẳng
giữa.Hệ
thống
đạo
trình
này
được
mô
tả
ở
Hình
16.13.
Otto
H.Schimitt
và
Ernst
Simonson
đã
phát
triển
nhiều
phiên
bản
của
hệ
thống
đạo
trình
điện
tâm
đồ
vecto,và
gọi
chúng
là
ghi
vecto
điện
tim
nổi
(stereovectorelectrocardiography
SVEC).Phiên
bản
thứ
ba,SVEC
III,được
công
bố
năm
1955
(Schmitt
và
Simonson,1955
).Nó
đòi
hỏi
tổng
ố
14
điện
cực
và
tạo
thành
một
trường
đạo
trình
trên
ngực
cái
mà
rất
đối
xứng
với
mặt
phẳng
giữa.Hệ
thống
đạo
trình
này
được
mô
tả
ở
Hình
16.13.
![]() Trong
hệ
thống
đạo
trình
SVEC
III,cá
điện
cực
được
đặt
trên
ngực
theo
cách
sau:Cơ
thể
được
chia
thành
các
góc
30o
có
các
phần
đối
xứng
qua
một
trục
trung
tâm
thẳng
đứng,để
mà
bắt
đầu
với
một
ở
phía
trước,các
chữ
số
Ả
Rập
tới
12
phần
chia
cơ
thể
theo
chiều
dọc.Chữ
số
La
Mã
được
đặt
cho
khoảng
trống
ở
giữa
xương
ức
và
được
tiến
hành
theo
chiều
ngang
trong
một
bảng
điều
khiển
rộng
để
một
đường
kẻ
ô
được
thiết
lập
trong
một
vị
trí
như
V
7
ở
một
vị
trí
tại
mức
độ
thẳng
đứng
của
khoảng
trống
ở
giữa
thứ
5
và
ở
giữa
phía
sau.
Trong
hệ
thống
đạo
trình
SVEC
III,cá
điện
cực
được
đặt
trên
ngực
theo
cách
sau:Cơ
thể
được
chia
thành
các
góc
30o
có
các
phần
đối
xứng
qua
một
trục
trung
tâm
thẳng
đứng,để
mà
bắt
đầu
với
một
ở
phía
trước,các
chữ
số
Ả
Rập
tới
12
phần
chia
cơ
thể
theo
chiều
dọc.Chữ
số
La
Mã
được
đặt
cho
khoảng
trống
ở
giữa
xương
ức
và
được
tiến
hành
theo
chiều
ngang
trong
một
bảng
điều
khiển
rộng
để
một
đường
kẻ
ô
được
thiết
lập
trong
một
vị
trí
như
V
7
ở
một
vị
trí
tại
mức
độ
thẳng
đứng
của
khoảng
trống
ở
giữa
thứ
5
và
ở
giữa
phía
sau.
Thành phần mặt sau ra mặt trước (thành phần x )
![]() Thành
phần
từ
phía
trước
ra
phía
sau,thành
phần
x,được
hình
thành
từ
bốn
điện
cực
ở
phía
sau
và
bốn
điện
cực
trước
ngực.Các
điện
cực
phía
sau
được
đặt
tại
các
ô
điểm
III
6,III
8,VI
6
và
VI
8.Mỗi
trong
số
các
điện
cực
được
kết
nối
với
điện
trở
100
kΩ
đến
điểm
cuối
phía
sau
duy
nhất
(-x).Những
điện
cực
trước
ngực
được
đặt
ở
các
ô
điểm
III
12,III
2,VI
2
và
VI
12.Một
điện
trở
&70
kΩ
được
kết
nối
từ
cái
đầu
tiền
(III
12
),và
điện
trở
100
kΩ
được
kết
nối
từ
những
điện
cực
khác
tới
điểm
cuối
duy
nhất
của
ngực
(+x).
Thành
phần
từ
phía
trước
ra
phía
sau,thành
phần
x,được
hình
thành
từ
bốn
điện
cực
ở
phía
sau
và
bốn
điện
cực
trước
ngực.Các
điện
cực
phía
sau
được
đặt
tại
các
ô
điểm
III
6,III
8,VI
6
và
VI
8.Mỗi
trong
số
các
điện
cực
được
kết
nối
với
điện
trở
100
kΩ
đến
điểm
cuối
phía
sau
duy
nhất
(-x).Những
điện
cực
trước
ngực
được
đặt
ở
các
ô
điểm
III
12,III
2,VI
2
và
VI
12.Một
điện
trở
&70
kΩ
được
kết
nối
từ
cái
đầu
tiền
(III
12
),và
điện
trở
100
kΩ
được
kết
nối
từ
những
điện
cực
khác
tới
điểm
cuối
duy
nhất
của
ngực
(+x).
Thành phần từ phải qua trái (thành phần y)
![]() Điểm
cuối
bên
phải
(-y
)
đã
đạt
được
bởi
việc
kết
nối
điện
trở
100
kΩ
giữa
tay
phải
và
ô
điểm
V
11.Điểm
cuối
bên
trái
(+y)
được
hình
thành
tương
tự
bằng
việc
kết
nối
điện
trở
100
kΩ
giữa
tay
trái
và
ô
điểm
V
3.Để
chuẩn
hóa
đạo
trình,sự
tăng
lên
được
điều
chỉnh
ở
mức
75 %.
Điểm
cuối
bên
phải
(-y
)
đã
đạt
được
bởi
việc
kết
nối
điện
trở
100
kΩ
giữa
tay
phải
và
ô
điểm
V
11.Điểm
cuối
bên
trái
(+y)
được
hình
thành
tương
tự
bằng
việc
kết
nối
điện
trở
100
kΩ
giữa
tay
trái
và
ô
điểm
V
3.Để
chuẩn
hóa
đạo
trình,sự
tăng
lên
được
điều
chỉnh
ở
mức
75 %.
Thành phần từ chân tới đầu (thành phần z )
![]() Thành
phần
z
đạt
được
một
cách
đơn
giản
bằng
cách
đặt
các
điện
cực
ở
chân
trái
và
đầu.Lần
nữa,để
chuẩn
hóa
đạo
trình,sự
tăng
lên
được
điều
chỉnh
ở
mức
71 %.
Thành
phần
z
đạt
được
một
cách
đơn
giản
bằng
cách
đặt
các
điện
cực
ở
chân
trái
và
đầu.Lần
nữa,để
chuẩn
hóa
đạo
trình,sự
tăng
lên
được
điều
chỉnh
ở
mức
71 %.

16.3.4 Hệ thống đạo trình Fischmann-Barber-Weiss
ĐIỀU KIỆN ĐẦU :
NGUỒN :Momen lưỡng cực của một nguồn khối với sự di chuyển (tối ưu ) vị trí.
VẬT DẪN :Xác định,đông nhất
![]() E.
J.
Fischmann,
M.
R.
Barber,
và
G.
H.
Weiss
(1971)
đã
xây
dựng
một
hệ
thống
đạo
trình
VCG
cái
mà
sự
đo
lường
lưỡng
cực
điện
tương
đương
theo
định
lý
Gabor-Nelson.
E.
J.
Fischmann,
M.
R.
Barber,
và
G.
H.
Weiss
(1971)
đã
xây
dựng
một
hệ
thống
đạo
trình
VCG
cái
mà
sự
đo
lường
lưỡng
cực
điện
tương
đương
theo
định
lý
Gabor-Nelson.
![]() Thiết
bị
của
họ
bao
gồm
ma
trận
các
điện
cực
7x8
ở
phía
sau
của
bệnh
nhân
và
11x12
ở
phía
ngực.Sau
đó
được
cố
định
trên
một
cần
cái
mà
có
thể
di
chuyển
dọc
trục
của
chúng.Tương
tự
những
ma
trận
điện
cực
với
7x7
các
điện
cực
cũng
đã
được
đặt
trên
mặt
của
bênh
nhân.Khi
di
chuyển
cần
các
điện
cực
được
ép
chống
lại
bề
mặt
của
ngực,sự
di
chuyển
này
đưa
thông
tin
về
hình
dạng
của
ngực.Thông
tin
này
là
cần
thiết
trong
giải
pháp
của
công
thức
Gabor-Nelson.
Thiết
bị
của
họ
bao
gồm
ma
trận
các
điện
cực
7x8
ở
phía
sau
của
bệnh
nhân
và
11x12
ở
phía
ngực.Sau
đó
được
cố
định
trên
một
cần
cái
mà
có
thể
di
chuyển
dọc
trục
của
chúng.Tương
tự
những
ma
trận
điện
cực
với
7x7
các
điện
cực
cũng
đã
được
đặt
trên
mặt
của
bênh
nhân.Khi
di
chuyển
cần
các
điện
cực
được
ép
chống
lại
bề
mặt
của
ngực,sự
di
chuyển
này
đưa
thông
tin
về
hình
dạng
của
ngực.Thông
tin
này
là
cần
thiết
trong
giải
pháp
của
công
thức
Gabor-Nelson.
![]() Hệ
thống
đạo
trình
này
đã
không
được
y
tế
lâm
sàng
sử
dụng
nhưng
thay
vào
đó
các
biểu
thức
của
lý
thuyết
của
Gabor-Nelson
được
sử
dụng
trong
đo
lường
của
phép
ghi
điện
tâm
đồ.
Hệ
thống
đạo
trình
này
đã
không
được
y
tế
lâm
sàng
sử
dụng
nhưng
thay
vào
đó
các
biểu
thức
của
lý
thuyết
của
Gabor-Nelson
được
sử
dụng
trong
đo
lường
của
phép
ghi
điện
tâm
đồ.
16.3.5 Hệ thống đạo trình Nelson
ĐIỀU KIỆN ĐẦU :
NGUỒN :Momen lưỡng cực của một nguồn khối với việc di chuyển (tối ưu )vị trí.
VẬT DẪN :Xác định,đồng nhất
![]() Năm
1971
Clifford
V.Nelson
và
các
cộng
sự
của
ông
đã
công
bố
một
hệ
thống
đạo
trình
phù
hợp
cho
y
tế
lâm
sàng
sử
dụng
dựa
trên
định
lý
Gabor-Nelson
(Nelson
et
al.,1971).Hệ
thống
đạo
trình
này
cung
cấp
các
điện
cực
đặt
ở
ba
mức
của
lồng
ngực
với
tám
trong
mỗi
mức,một
điện
cức
trên
đầu
và
một
ở
chân
trái.Các
hàng
điện
cực
được
thiết
kế
là
A,B
và
C,được
hiển
thị
ở
Hình
16.14.Các
mức
được
xác
định
bởi
việc
đo
khoảng
cách
H’
giữa
dấu
trên
xương
ức
và
rốn.Khoảng
cách
này
được
chia
thành
8,và
các
hàng
được
đặt
tại
1/8
H’,4/8
H’
và
7/8
H’
từ
dấu
đó
hoặc
rốn.Hiển
thị
trong
Hình
16.14,các
điện
cực
1
và
5
được
đặt
ở
trung
tâm
phía
sau
và
giữa
đường
xương
ức,một
cách
tương
ứng.Các
điện
cức
2,3
và
4
được
đặt
ngang
bằng
ở
mặt
phải,và
các
điện
cực
6,7
và
8
được
đặt
ngang
bằng
ở
mặt
trái.Nếu
những
cánh
tay
can
thiệp
vào
mức
C,điện
cực
3
và
7
được
đặt
ở
tay
phải
và
tay
trái
một
cách
tương
ứng.Góc
θ
là
góc
giữa
bề
mặt
của
lồng
ngực
và
mặt
phẳng
phía
trước.Điện
trở
500
kΩ
(R)
được
kết
nối
với
các
điện
cực
trên
hàng
A,B
và
C
(xem
Hình
16.15
).Từ
những
điện
trở
đó,trong
mỗi
ba
mức
bốn
(Rx
và
Ry
)
là
biến
thiên
và
được
điều
chỉnh
theo
hình
dạng
của
lồng
ngực
của
bệnh
nhân
tuân
theo
lý
thuyết
Gabor-Nelson.Sự
điều
chỉnh
này
được
thực
hiện
để:
Năm
1971
Clifford
V.Nelson
và
các
cộng
sự
của
ông
đã
công
bố
một
hệ
thống
đạo
trình
phù
hợp
cho
y
tế
lâm
sàng
sử
dụng
dựa
trên
định
lý
Gabor-Nelson
(Nelson
et
al.,1971).Hệ
thống
đạo
trình
này
cung
cấp
các
điện
cực
đặt
ở
ba
mức
của
lồng
ngực
với
tám
trong
mỗi
mức,một
điện
cức
trên
đầu
và
một
ở
chân
trái.Các
hàng
điện
cực
được
thiết
kế
là
A,B
và
C,được
hiển
thị
ở
Hình
16.14.Các
mức
được
xác
định
bởi
việc
đo
khoảng
cách
H’
giữa
dấu
trên
xương
ức
và
rốn.Khoảng
cách
này
được
chia
thành
8,và
các
hàng
được
đặt
tại
1/8
H’,4/8
H’
và
7/8
H’
từ
dấu
đó
hoặc
rốn.Hiển
thị
trong
Hình
16.14,các
điện
cực
1
và
5
được
đặt
ở
trung
tâm
phía
sau
và
giữa
đường
xương
ức,một
cách
tương
ứng.Các
điện
cức
2,3
và
4
được
đặt
ngang
bằng
ở
mặt
phải,và
các
điện
cực
6,7
và
8
được
đặt
ngang
bằng
ở
mặt
trái.Nếu
những
cánh
tay
can
thiệp
vào
mức
C,điện
cực
3
và
7
được
đặt
ở
tay
phải
và
tay
trái
một
cách
tương
ứng.Góc
θ
là
góc
giữa
bề
mặt
của
lồng
ngực
và
mặt
phẳng
phía
trước.Điện
trở
500
kΩ
(R)
được
kết
nối
với
các
điện
cực
trên
hàng
A,B
và
C
(xem
Hình
16.15
).Từ
những
điện
trở
đó,trong
mỗi
ba
mức
bốn
(Rx
và
Ry
)
là
biến
thiên
và
được
điều
chỉnh
theo
hình
dạng
của
lồng
ngực
của
bệnh
nhân
tuân
theo
lý
thuyết
Gabor-Nelson.Sự
điều
chỉnh
này
được
thực
hiện
để:
![]() Trong
đó
θ
=
góc
giữa
bề
mặt
thường
và
bề
mặt
giữa.
Trong
đó
θ
=
góc
giữa
bề
mặt
thường
và
bề
mặt
giữa.
![]() Nelson
và
các
cộng
sự
cho
rẳng
trên
cơ
sở
đo
lường
của
họ
hệ
thống
đạo
trinh
VCG
này
sẽ
đúng
hơn
nhiều
so
với
hệ
thống
đạo
trình
Frank
hoặc
McFee.Hơn
nữa
hệ
thống
này
rất
không
nhạy
với
lỗi
vị
trí
các
điện
cực.
Nelson
và
các
cộng
sự
cho
rẳng
trên
cơ
sở
đo
lường
của
họ
hệ
thống
đạo
trinh
VCG
này
sẽ
đúng
hơn
nhiều
so
với
hệ
thống
đạo
trình
Frank
hoặc
McFee.Hơn
nữa
hệ
thống
này
rất
không
nhạy
với
lỗi
vị
trí
các
điện
cực.
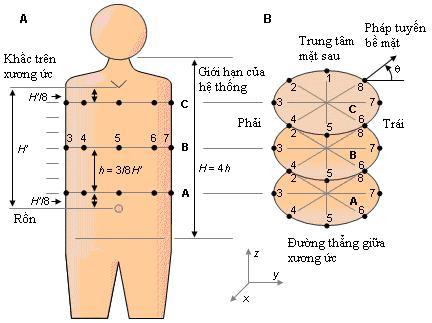
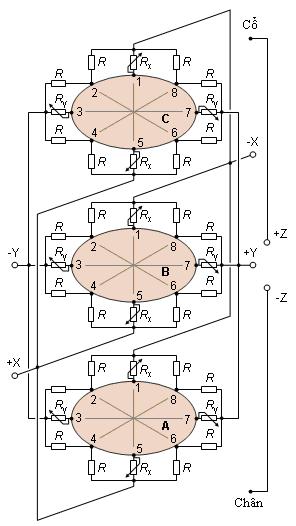
16.4 Thảo luận về ghi vecto điện tim đồ các đạo trình
16.4.1 Khả năng thay thế của các hệ thống điện tâm đồ vecto
![]() Mục
đích
của
hệ
thống
điện
tâm
đồ
vecto
là
để
phát
hiện
lưỡng
cực
tương
đương
của
tim.Nếu
các
hệ
thống
khác
nhau
thực
hiện
đo
lường
một
cách
chính
xác,các
kết
quả
đo
lường
này
phải
giống
nhau.Điều
này
đúng,tuy
nhiên,không
phải
là
mọi
trường
hợp.Trong
thực
tế,mỗi
hệ
thống
điện
tâm
đồ
vecto
đưa
ra
một
kết
quả
đo
lường
khác
nhau
chút
ít.
Mục
đích
của
hệ
thống
điện
tâm
đồ
vecto
là
để
phát
hiện
lưỡng
cực
tương
đương
của
tim.Nếu
các
hệ
thống
khác
nhau
thực
hiện
đo
lường
một
cách
chính
xác,các
kết
quả
đo
lường
này
phải
giống
nhau.Điều
này
đúng,tuy
nhiên,không
phải
là
mọi
trường
hợp.Trong
thực
tế,mỗi
hệ
thống
điện
tâm
đồ
vecto
đưa
ra
một
kết
quả
đo
lường
khác
nhau
chút
ít.
![]() Đã
có
những
nỗ
lực
để
phát
triển
hệ
số
chuyển
đổi
từ
một
hệ
thống
này
sang
hệ
thống
khác
nhằm
mục
đích
làm
các
hệ
thống
khác
nhau
tỉ
lệ
với
nhau.Nếu
các
hệ
thống
khác
nhau
là
trực
giao,sự
chuyển
đổi
đó,về
nguyên
tắc,cũng
nên
là
trực
giao.
Đã
có
những
nỗ
lực
để
phát
triển
hệ
số
chuyển
đổi
từ
một
hệ
thống
này
sang
hệ
thống
khác
nhằm
mục
đích
làm
các
hệ
thống
khác
nhau
tỉ
lệ
với
nhau.Nếu
các
hệ
thống
khác
nhau
là
trực
giao,sự
chuyển
đổi
đó,về
nguyên
tắc,cũng
nên
là
trực
giao.
![]() Horan,Flowers,
và
Brody
(1965)
thực
hiện
một
nghiên
cứu
cẩn
thận
về
hệ
số
chuyển
đổi
giữa
hệ
thống
đạo
trình
Frank,McFee-Parungao
(axial-)
và
SVEC
III
trên
35
người
đàn
ông
trẻ.Trong
nghiên
cứu
này
nó
đã
tìm
thấy
sự
chuyển
đổi
giữa
các
hệ
thống
đạo
trình
là
không
trực
giao,chỉ
ra
rằng
có
ít
nhất
hai
hệ
thống
điện
tâm
đồ
vecto
là
không
thực
sự
trực
giao.Họ
cũng
đi
đến
kết
luận
rằng
khả
năng
thay
thế
thực
tế
của
lượng
thông
tin
đã
đạt
được
từ
một
hệ
thống
đạo
trình
để
thu
được
bằng
một
hệ
thống
khác
bị
giới
hạn
nghiêm
trọng
bởi
vì
giới
hạn
lớn
của
sự
biến
đổi
sinh
lý
trong
đặc
tính
chuyển
đổi.
Horan,Flowers,
và
Brody
(1965)
thực
hiện
một
nghiên
cứu
cẩn
thận
về
hệ
số
chuyển
đổi
giữa
hệ
thống
đạo
trình
Frank,McFee-Parungao
(axial-)
và
SVEC
III
trên
35
người
đàn
ông
trẻ.Trong
nghiên
cứu
này
nó
đã
tìm
thấy
sự
chuyển
đổi
giữa
các
hệ
thống
đạo
trình
là
không
trực
giao,chỉ
ra
rằng
có
ít
nhất
hai
hệ
thống
điện
tâm
đồ
vecto
là
không
thực
sự
trực
giao.Họ
cũng
đi
đến
kết
luận
rằng
khả
năng
thay
thế
thực
tế
của
lượng
thông
tin
đã
đạt
được
từ
một
hệ
thống
đạo
trình
để
thu
được
bằng
một
hệ
thống
khác
bị
giới
hạn
nghiêm
trọng
bởi
vì
giới
hạn
lớn
của
sự
biến
đổi
sinh
lý
trong
đặc
tính
chuyển
đổi.
16.4.2 Đặc tính của các hệ thống điện tâm đồ vecto khác nhau
![]() Các
hệ
thống
đạo
trình
đã
được
thảo
luận
trước
đây
đã
được
kiểm
tra
sử
dụng
các
mô
hình
máy
tính
của
lồng
ngực
để
xác
định
mức
độ
mà
chúng
đáp
ứng
các
điều
kiện
cơ
bản
cho
các
đạo
trình
trực
giao
đã
hiệu
chỉnh.
Các
hệ
thống
đạo
trình
đã
được
thảo
luận
trước
đây
đã
được
kiểm
tra
sử
dụng
các
mô
hình
máy
tính
của
lồng
ngực
để
xác
định
mức
độ
mà
chúng
đáp
ứng
các
điều
kiện
cơ
bản
cho
các
đạo
trình
trực
giao
đã
hiệu
chỉnh.
![]() Dưới
sự
thống
nhất,đồng
nhất,
và
các
điều
kiện
giới
hạn,Brody
và
Arzbaecher
(1964)
đã
đánh
giá
các
trường
đạo
trình
cho
một
vài
hệ
thống
VCG
và
so
sánh
mức
độ
của
sự
thống
nhất.Họ
thấy
rằng
các
hệ
thống
đạo
trình
Frank,SVEC
III
và
McFee-Parungao
đã
giới
thiệu
mức
độ
bị
méo.Tuy
nhiên,các
hệ
thống
đạo
trình
hình
lập
phương
Grishman
và
tứ
diện
Wilson
là
đáng
kể
hơn.Hệ
thống
McFee
–Parungao
đã
được
phát
hiện
là
có
tính
trực
giao
tốt
nhất
trong
tất
cả
các
hệ
thống,nhưng
cường
độ
của
các
đạo
trình
được
phát
hiện
là
không
đồng
đều.Macfarlane
(1969)
đã
giới
thiệu
một
biến
thể
mà
cường
độ
các
đạo
trình
là
cân
bằng.
Dưới
sự
thống
nhất,đồng
nhất,
và
các
điều
kiện
giới
hạn,Brody
và
Arzbaecher
(1964)
đã
đánh
giá
các
trường
đạo
trình
cho
một
vài
hệ
thống
VCG
và
so
sánh
mức
độ
của
sự
thống
nhất.Họ
thấy
rằng
các
hệ
thống
đạo
trình
Frank,SVEC
III
và
McFee-Parungao
đã
giới
thiệu
mức
độ
bị
méo.Tuy
nhiên,các
hệ
thống
đạo
trình
hình
lập
phương
Grishman
và
tứ
diện
Wilson
là
đáng
kể
hơn.Hệ
thống
McFee
–Parungao
đã
được
phát
hiện
là
có
tính
trực
giao
tốt
nhất
trong
tất
cả
các
hệ
thống,nhưng
cường
độ
của
các
đạo
trình
được
phát
hiện
là
không
đồng
đều.Macfarlane
(1969)
đã
giới
thiệu
một
biến
thể
mà
cường
độ
các
đạo
trình
là
cân
bằng.
![]() Ảnh
hưởng
của
việc
không
đồng
nhất
trong
các
trường
vecto
đạo
trình
đã
được
đưa
ra
bởi
Milan
Horá
ek
(1989).Sự
kiểm
tra
này
đã
được
tiến
hành
bằng
môt
máy
tính
mô
phỏng
trong
đó
sự
ảnh
hưởng
của
việc
không
đồng
nhất
trong
hình
ảnh
bề
mặt
được
đánh
giá.
Ảnh
hưởng
của
việc
không
đồng
nhất
trong
các
trường
vecto
đạo
trình
đã
được
đưa
ra
bởi
Milan
Horá
ek
(1989).Sự
kiểm
tra
này
đã
được
tiến
hành
bằng
môt
máy
tính
mô
phỏng
trong
đó
sự
ảnh
hưởng
của
việc
không
đồng
nhất
trong
hình
ảnh
bề
mặt
được
đánh
giá.
![]() Ảnh
hưởng
của
khối
lượng
máu
nội
khoang
có
xu
hướng
chống
lại
cái
đó
ở
phổi.Khối
lượng
máu
giảm
lưỡng
cực
tiếp
xúc
và
gia
tăng
lưỡng
cực
thường.Ảnh
hưởng
của
độ
dẫn
phổi
trên
các
vecto
đạo
trình
được
nghiên
cứu
bởi
Stanley,Pilkingotn,và
Morrow
(1986).Bằng
việc
sử
dụng
mô
hình
thực
tế
trên
cơ
thể
chó,họ
đã
chỉ
ra
rằng
momen
lưỡng
cực
z
(chân
tới
đầu
)
đã
giảm
một
cách
đơn
điệu
có
nghĩa
là
độ
dẫn
phổi
tăng.Mặt
khác,các
momen
lưỡng
cực
y
(phải
sang
trái
)
và
x
(
mặt
sau
ra
mặt
trước
)
cso
trạng
thái
một
hình
quả
chuông,với
các
giái
trị
thấp
cho
cả
độ
dẫn
phổi
thấp
hay
cao.Họ
tùm
thấy
rằng,độ
dẫn
phổi,tuy
nhiên,có
ảnh
hưởng
tương
đối
ít
trong
tổng
số
thể
tích
chất
dẫn
chi
tiết
của
cơ
thể.Sự
không
đồng
nhất
,trong
nghiên
cứu
của
họ,có
một
hiệu
quả
đáng
kể
là
lớp
cơ
xương.Kết
quả
này
là
hợp
lý
phù
hợp
với
các
nghiên
cứu
của
Gulrajani
và
Mailloux
(1983)
và
Rudy
và
Plonsey
(1980).
Ảnh
hưởng
của
khối
lượng
máu
nội
khoang
có
xu
hướng
chống
lại
cái
đó
ở
phổi.Khối
lượng
máu
giảm
lưỡng
cực
tiếp
xúc
và
gia
tăng
lưỡng
cực
thường.Ảnh
hưởng
của
độ
dẫn
phổi
trên
các
vecto
đạo
trình
được
nghiên
cứu
bởi
Stanley,Pilkingotn,và
Morrow
(1986).Bằng
việc
sử
dụng
mô
hình
thực
tế
trên
cơ
thể
chó,họ
đã
chỉ
ra
rằng
momen
lưỡng
cực
z
(chân
tới
đầu
)
đã
giảm
một
cách
đơn
điệu
có
nghĩa
là
độ
dẫn
phổi
tăng.Mặt
khác,các
momen
lưỡng
cực
y
(phải
sang
trái
)
và
x
(
mặt
sau
ra
mặt
trước
)
cso
trạng
thái
một
hình
quả
chuông,với
các
giái
trị
thấp
cho
cả
độ
dẫn
phổi
thấp
hay
cao.Họ
tùm
thấy
rằng,độ
dẫn
phổi,tuy
nhiên,có
ảnh
hưởng
tương
đối
ít
trong
tổng
số
thể
tích
chất
dẫn
chi
tiết
của
cơ
thể.Sự
không
đồng
nhất
,trong
nghiên
cứu
của
họ,có
một
hiệu
quả
đáng
kể
là
lớp
cơ
xương.Kết
quả
này
là
hợp
lý
phù
hợp
với
các
nghiên
cứu
của
Gulrajani
và
Mailloux
(1983)
và
Rudy
và
Plonsey
(1980).
![]() Jari
Hyttinen
đã
phân
tích
chi
tiết
của
hệ
thống
đạo
trình
của
Frank
và
SVEC
III
với
mô
hình
máy
tính
được
gọi
là
mô
hình
ghép
(the
hybrid
model
)
(Hyttinen,1989
).Ông
đã
phân
tích
độ
lớn
và
hướng
của
các
vecto
đạo
trình
ở
khu
vực
khác
nhau
của
tim
trong
một
mô
hình
lồng
ngực
không
đồng
nhất.Ông
ta
cũng
tiến
hành
nghiên
cứu
về
độ
nhạy
của
các
đạo
trình
đến
điểm
bắt
đầu
của
bán
kính
và
hướng
tiếp
tuyến
(liên
quan
đến
tim
),cái
mà
tất
nhiên
có
một
số
tác
động
lâm
sàng.
Jari
Hyttinen
đã
phân
tích
chi
tiết
của
hệ
thống
đạo
trình
của
Frank
và
SVEC
III
với
mô
hình
máy
tính
được
gọi
là
mô
hình
ghép
(the
hybrid
model
)
(Hyttinen,1989
).Ông
đã
phân
tích
độ
lớn
và
hướng
của
các
vecto
đạo
trình
ở
khu
vực
khác
nhau
của
tim
trong
một
mô
hình
lồng
ngực
không
đồng
nhất.Ông
ta
cũng
tiến
hành
nghiên
cứu
về
độ
nhạy
của
các
đạo
trình
đến
điểm
bắt
đầu
của
bán
kính
và
hướng
tiếp
tuyến
(liên
quan
đến
tim
),cái
mà
tất
nhiên
có
một
số
tác
động
lâm
sàng.
![]() Trong
nghiên
cứu
của
ông
về
ý
tưởng
đạo
trình
VCG,Hyttinen
đã
phát
hiện
ra
rằng
trong
tất
cả
các
nghiên
cứu
các
hệ
thống
đạo
trình,các
vecto
đạo
trình
của
đạo
trình
x
có
hướng
từ
trên
xuống
trong
phần
sau
cao
hơn
của
tim.Các
khối
máu
ở
phía
trong
và
trên
tim
trong
hệ
thống
mạch
lớn
này
là
nguyên
nhân
chính
gây
ra
tập
tính
này
của
các
vecto
đạo
trình.Đạo
trình
x,cái
mà
gần
nhất
với
lý
tưởng,nằm
trong
hệ
thống
trục.Tổng
độ
nhạy
trong
hướng
x
là
thấp
hơn
một
ít
so
với
đạo
trình
x
SVEC
III,nhưng
sự
đồng
nhất
của
đạo
trình
là
tốt
hơn
nhiều.Vị
trí
của
các
điện
cực
trên
ngực
là
tốt
và
ảnh
hưởng
lân
cận
là
yếu
trong
hệ
trục
đạo
trình
x
đã
so
sánh
với
hệ
thống
đạo
trình
khác.
Trong
nghiên
cứu
của
ông
về
ý
tưởng
đạo
trình
VCG,Hyttinen
đã
phát
hiện
ra
rằng
trong
tất
cả
các
nghiên
cứu
các
hệ
thống
đạo
trình,các
vecto
đạo
trình
của
đạo
trình
x
có
hướng
từ
trên
xuống
trong
phần
sau
cao
hơn
của
tim.Các
khối
máu
ở
phía
trong
và
trên
tim
trong
hệ
thống
mạch
lớn
này
là
nguyên
nhân
chính
gây
ra
tập
tính
này
của
các
vecto
đạo
trình.Đạo
trình
x,cái
mà
gần
nhất
với
lý
tưởng,nằm
trong
hệ
thống
trục.Tổng
độ
nhạy
trong
hướng
x
là
thấp
hơn
một
ít
so
với
đạo
trình
x
SVEC
III,nhưng
sự
đồng
nhất
của
đạo
trình
là
tốt
hơn
nhiều.Vị
trí
của
các
điện
cực
trên
ngực
là
tốt
và
ảnh
hưởng
lân
cận
là
yếu
trong
hệ
trục
đạo
trình
x
đã
so
sánh
với
hệ
thống
đạo
trình
khác.
![]() Đối
với
các
đạo
trình
y,đạo
trình
y
SVEC
III
có
đặc
trưng
tốt
nhất.SVEC
III
và
trục
đạo
trình
y
có
độ
nhạy
cân
bằng
trong
hướng
y,nhưng
khác
nhau
về
phân
phối
độ
nhạy
trong
không
gian-đó
là,sự
đồng
nhất
của
độ
nhạy-tốt
hơn
trong
hệ
thống
SVEC
III.Ảnh
hưởng
lân
cận
là
không
quá
rõ
ràng
bởi
vì
việc
sử
dụng
đạo
trình
I
như
một
phần
của
đạo
trình
y
SVEC
III.
Đối
với
các
đạo
trình
y,đạo
trình
y
SVEC
III
có
đặc
trưng
tốt
nhất.SVEC
III
và
trục
đạo
trình
y
có
độ
nhạy
cân
bằng
trong
hướng
y,nhưng
khác
nhau
về
phân
phối
độ
nhạy
trong
không
gian-đó
là,sự
đồng
nhất
của
độ
nhạy-tốt
hơn
trong
hệ
thống
SVEC
III.Ảnh
hưởng
lân
cận
là
không
quá
rõ
ràng
bởi
vì
việc
sử
dụng
đạo
trình
I
như
một
phần
của
đạo
trình
y
SVEC
III.
![]() Trong
đạo
trình
z,sự
không
đồng
nhất
là
lí
do
chính
dẫn
đến
các
nhiễu
của
độ
nhạy
trong
không
gian.Điều
này
có
thể
được
nhìn
thấy
một
cách
đặc
biệt
trong
khu
vực
vách
ngăn.Các
đạo
trình,tuy
nhiên,rất
giống
với
đạo
trình
z
của
Frank,có
đặc
tính
độ
nhạy
không
gian
tốt
hơn
rất
ít
so
với
các
hệ
thống
đạo
trình
khác.
Trong
đạo
trình
z,sự
không
đồng
nhất
là
lí
do
chính
dẫn
đến
các
nhiễu
của
độ
nhạy
trong
không
gian.Điều
này
có
thể
được
nhìn
thấy
một
cách
đặc
biệt
trong
khu
vực
vách
ngăn.Các
đạo
trình,tuy
nhiên,rất
giống
với
đạo
trình
z
của
Frank,có
đặc
tính
độ
nhạy
không
gian
tốt
hơn
rất
ít
so
với
các
hệ
thống
đạo
trình
khác.
Tham khảo
Akulinichev IT (1956): Vectorelectrocardioscope. Voenno-Med. Zh. 1: 79. (In Russian).
Akulinichev IT (1960): Practical Questions in Vectorcardioscopy, Medgiz, Moscow. 214 p. (In Russian)
Brody DA, Arzbaecher RC (1964): A comparative analysis of several corrected vector-cardiographic leads. Circulation 29:(4, Suppl.) 533-45.
Duchosal PW, Sulzer R (1949): La Vectorcardiographie, S. Karger, New York, N.Y.
Fischmann EJ, Barber MR, Weiss GH (1971): Multielectrode grids which measure torso area and resistivity and yield dipole moments calibrated for these variables. In Proc. XIth Internat. Symp. On Vectorcardiography, New York, 1970, ed. I Hoffman, pp. 30-41, North-Holland Publishing Co., Amsterdam.
Frank E (1954): The image surface of a homogeneous torso. Am. Heart J. 47: 757-68.
Frank E (1956): An accurate, clinically practical system for spatial vectorcardiography. Circulation 13:(5) 737-49.
Grishman A, Scherlis L (1952): Spatial Vectorcardiography, 217 pp. Saunders, Philadelphia.
Gulrajani RM, Mailloux GE (1983): A simulation study of the effects of torso inhomogeneities on electrocardiographic potentials using realistic heart and torso models. Circ. Res. 52: 45-56.
Hollman W, Hollman HE (1939): Neue electrocardiographische Untersuchungsmethode. Z. Kreislaufforsch. 29: 546-558.
Horácek BM (1989): Lead theory. In Comprehensive Electrocardiology. Theory and Practice in Health and Disease, 1st ed. Vol. 1, ed. PW Macfarlane, TDV Lawrie, pp. 291-314, Pergamon Press, New York.
Horan LG, Flowers NC, Brody DA (1965): The interchangeability of vectorcardiographic systems. Am. Heart J. 70:(3) 365-76.
Hyttinen J (1989): Development of aimed ECG-leads. Tampere Univ. Tech., Tampere, Finland, Thesis, pp. 138. (Lic. Tech. thesis)
Kimura N (1939): Study on heart function by vectorcardiography of three-dimensional projection. Jpn. Circ. J. 5: 93.
Macfarlane PW (1969): A modified axial lead system for orthogonal lead electrocardiography. Cardiovasc. Res. 3:(10) 510-5.
Mann H (1920): A method for analyzing the electrocardiogram. Arch. Int. Med. 25: 283-94.
Mann H (1931): Interpretation of bundle-branch block by means of the monocardiogram. Am. Heart J. 6: 447-57.
Mann H (1938a): The monocardiogram. Stud. Rockefeller Inst. Med. Res. 109: 409-32.
Mann H (1938b): The monocardiograph. Am. Heart J. 15: 681-99.
McFee R, Parungao A (1961): An orthogonal lead system for clinical electrocardiography. Am. Heart J. 62: 93-100.
Milnor MR, Talbot SA, Newman EV (1953): A study of the relationship between unipolar leads and spatial vectorcardiograms, using the panoramic vectorcardiograph. Circulation 7: 545.
Nelson CV, Gastongay PR, Wilkinson AF, Voukydis PC (1971): A lead system for direction and magnitude of the heart vector. In Vectorcardiography 2. Proc. XIth Internat. Symp. On Vectorcardiography, New York, 1970, ed. I
Hoffman, IR Hamby, E Glassman, pp. 85-97, North-Holland Publishing Co., Amsterdam.
Pawlov Z (1966): Über einige Fragen des Vektorkardiographischen Dreiflächensystems von Akulinitschev. In Neue
Ergebnisse Der Elektrokardiologie, ed. E Schubert, (Proceedings of the 6th International Colloquium of
Vectorcardiography, Leipzig 1965.), VEB Gustav Fischer Verlag, Jena.
Rudy Y, Plonsey R (1980): A comparison of volume conductor and source geometry effects on body surface and epicardial potentials. Circ. Res. 46:(2) 283-91.
Schellong F, Heller S, Schwingel G (1937): Das Vectorcardiogram; Eine Untersuchungsmethode des Herzens. Z. Kreislaufforsch. 29: 497-509.
Schmitt OH, Simonson E (1955): The present status of vectorcardiography. A.M.A. Arch. Internal Med. 96: 574-90.
Stanley PC, Pilkington TC, Morrow MN (1986): The effects of thoracic inhomogeneities on the relationship between epicardial and torso potentials. IEEE Trans. Biomed. Eng. BME-33:(3) 273-84.
Waller AD (1887): A demonstration on man of electromotive changes accompanying the heart's beat. J. Physiol. (Lond.) 8: 229-34.
Wenger R (1969): Klinische Vektorkardiographie, 2nd ed., Dr. Dietrich Steinkopff Verlag, Darmstadt.
Wilson FN, Johnston FD (1938): The vectorcardiogram. Am. Heart J. 16: 14-28.
Wilson FN, Johnston FD, Kossmann CE (1947): The substitution of a tetrahedron for the Einthoven triangle. Am. Heart J. 33: 594-603.
Sách tham khảo
Macfarlane PW, Lawrie TDV (eds.) (1989): Comprehensive Electrocardiology: Theory and Practice in Health and Disease. 1st ed. Vols. 1, 2, and 3. Pergamon Press, New York. 1785 p.
| Trang trước | Các hệ thống đạo trình tâm đồ véc tơ | Trang tiếp |


