Sách:Điện từ sinh học/Lý thuyết của các phép đo từ sinh học
12 Lý thuyết phép đo từ sinh học
Mục lục
- 1 12.1 Trường từ sinh học
- 2 12.2 Bản chất của nguồn từ sinh học
- 3 12.3lý thuyết biến thiên cho từ trường
- 4 12.4 Moment lưỡng cực từ của nguồn khối
- 5 12.5 Trường đạo trình lý tưởng của một đầu dò đạo trình lưỡng cực từ tương đương của nguồn khối
- 6 12.6 Quá trình đồng bộ trường đạo trình lý tưởng trong sự dò tìm moment lưỡng cực từ của nguồn khối
- 7 12.7 Sự so sánh trường đạo trình của đạo trình lưỡng cực lý tưởng với việc dò tìm moment lưỡng cực từ và điện của nguồn khối
- 8 12.8 Độ nhạy tiếp tuyến và bán kính của hệ thống đạo trình dò tìm moment lưỡng cực điện và từ của một nguồn khối
- 9 12.9 Thành phần đặc biệt của trường đạo trình từ
- 10 12.10 Sự độc lập của trường điện sinh học và từ sinh học và phép đo
-
11
12.11
Sự
phân
bố
của
đạo
trình
từ
cơ
bản
- 11.1 12.11.1 Biêu thức của phép tính sự phân bố độ nhạy của đạo trình từ cơ bản
- 11.2 12.11.2 Mật độ dòng trường đạo trình của một trường đạo trình đơn cực của từ kế một cuộn dây
- 11.3 12.11.3 Hiệu ứng của cuộn dây ở xa với trường đạo trình của đạo trình điểm
- 11.4 Mật độ dòng trường đạo trình của đạo trình lưỡng cực
- 12 Tham khảo
12.1 Trường từ sinh học
Điều kiện đầu
Nguồn:sự
phân
bố
nguồn
dòng
được
đưa
vào
 (nguồn
khối)
(nguồn
khối)
Bộ dẫn khối: hữu hạn, không đồng nhất
Mật
độ
dòng
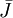 trong
cả
một
bộ
dẫn
khối
đưa
tới
từ
trường
được
đưa
ra
bởi
các
mối
quan
hệ
sau
(Stratton,
1941;
Jackson,
1975):
trong
cả
một
bộ
dẫn
khối
đưa
tới
từ
trường
được
đưa
ra
bởi
các
mối
quan
hệ
sau
(Stratton,
1941;
Jackson,
1975):
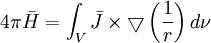 (12.01)
(12.01)
của
lượng
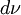 trong
cơ
thể
con
người,
trong
cơ
thể
con
người,
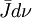 là
một
nguyên
tố
nguồn.
và
là
một
nguyên
tố
nguồn.
và
 là
một
nhà
điều
hành
với
nguồn
tọa
độ.
Thay
phương
trình
7.2
được
lặp
lại
ở
đây,
là
một
nhà
điều
hành
với
nguồn
tọa
độ.
Thay
phương
trình
7.2
được
lặp
lại
ở
đây,
 (12.02)
(12.02)
Vào
phương
trình
12.1
và
chia
bộ
dẫn
khối
không
đồng
nhất
thành
vùng
đồng
nhất
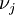 với
độ
dẫn
với
độ
dẫn
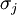 ,
ta
thu
được
,
ta
thu
được
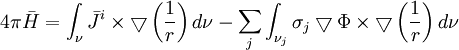 (12.03)
(12.03)Gìơ chúng ta tạo ra cách sử dụng của sự đồng nhất vector sau (Stratton, 1941, p. 604):
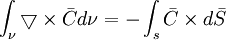 (12.04)
(12.04)Nơi bề mặt tích phân được lấy trên bề mặt S bao quang lượng v của tích phân khối. Áp dụng 12.4 cho 12.3, số hạng cuối trong biểu thức 12.2, bao gồm kí hiệu của nó, có thể được thay thế bởi
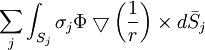 (12.05)
(12.05)
Cuối
cùng,
áp
dụng
kết
quả
này
cho
biểu
thức
12.2
và
biểu
thị
lần
nữa
các
vùng
primed
and
double-primed
của
độ
dẫn
bên
trong
và
ngòai
đường
bao,
lần
lượt
là,
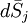 có
hướng
từ
vùng
primed
đến
vùng
double-primed,
chúng
ta
thu
được
(chú
ý
rằng
mỗi
giao
diện
phát
dinh
hai
lần,
một
là
tại
bề
mặt
của
có
hướng
từ
vùng
primed
đến
vùng
double-primed,
chúng
ta
thu
được
(chú
ý
rằng
mỗi
giao
diện
phát
dinh
hai
lần,
một
là
tại
bề
mặt
của
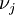 và
hai
là
từ
bề
mặt
của
mỗi
vùng
xung
quanh
của
và
hai
là
từ
bề
mặt
của
mỗi
vùng
xung
quanh
của
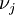 )
)
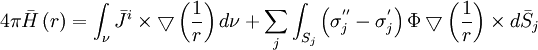 (12.06)
(12.06)
Phương
trình
này
miêu
tả
từ
trường
bên
ngoài
bộ
dẫn
khối
cố
định
chứa
nguồn
khối
(điện)
bên
trong
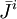 và
sự
thiếu
đồng
nhất
và
sự
thiếu
đồng
nhất
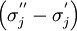 .
Nó
được
suy
ra
lần
đầu
tiên
bởi
David
Geselowitz
(Geselowitz,
1970).
.
Nó
được
suy
ra
lần
đầu
tiên
bởi
David
Geselowitz
(Geselowitz,
1970).
Điều
quan
trọng
là
chú
ý
rằng
số
hạng
đầu
tiên
bên
vế
phải
của
biểu
thức
12.6,
bao
gồm
cả
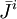 ,
biểu
diễn
sự
đóng
góp
của
nguồn
khối,
và
số
hạng
thứ
hai
tác
dụng
của
đường
bao
và
sự
không
đồng
nhất.
Nguồn
đưa
vào
,
biểu
diễn
sự
đóng
góp
của
nguồn
khối,
và
số
hạng
thứ
hai
tác
dụng
của
đường
bao
và
sự
không
đồng
nhất.
Nguồn
đưa
vào
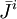 nảy
sinh
từ
hoạt
động
tế
bào
và
vì
thế
có
giá
trị
chẩn
đóan
nơi
mà
số
hạng
thứ
hai
có
thể
được
xem
như
là
một
biến
dạng
nhờ
vào
sự
không
đồng
nhất
của
bộ
dẫn
khối.
Những
nguồn
rất
giống
nhau
này
được
nhận
ra
sớm
hơn
khi
điện
trường
được
phát
ra
bởi
nó
đang
được
đánh
giá
(nhìn
biểu
thức
7.10).
(trong
trường
hợp
điện,
các
số
hạng
này
cũng
được
gán
cho
nguồn
chính
và
nguồn
thứ
cấp).
nảy
sinh
từ
hoạt
động
tế
bào
và
vì
thế
có
giá
trị
chẩn
đóan
nơi
mà
số
hạng
thứ
hai
có
thể
được
xem
như
là
một
biến
dạng
nhờ
vào
sự
không
đồng
nhất
của
bộ
dẫn
khối.
Những
nguồn
rất
giống
nhau
này
được
nhận
ra
sớm
hơn
khi
điện
trường
được
phát
ra
bởi
nó
đang
được
đánh
giá
(nhìn
biểu
thức
7.10).
(trong
trường
hợp
điện,
các
số
hạng
này
cũng
được
gán
cho
nguồn
chính
và
nguồn
thứ
cấp).
Tương
tự,
như
được
bàn
ở
biểu
thức
7.10,
dễ
để
nhận
ra
rằng
nếu
bộ
dẫn
khối
là
đồng
nhất,
sự
chênh
lệch
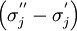 trong
biểu
thức
thứ
hai
là
bằng
0,
và
nó
được
rút
gọn.
Sau
đó
biểu
thức
giảm
cho
biểu
thức
của
từ
truờng
nhờ
vào
sự
phân
bố
của
nguồn
khối
trong
bộ
dẫn
khối
không
đồng
nhất.
Điều
này
được
giới
thiệu
ở
phần
cuối
biểu
thức
12.10.
Trong
việc
thiết
kế
thiết
bị
kiểm
tra
từ
sinh
học
chất
lượng
cao,
mục
đích
là
loại
bỏ
tác
dụng
của
nguồn
thứ
cấp
đến
khả
năng
mở
rộng.
trong
biểu
thức
thứ
hai
là
bằng
0,
và
nó
được
rút
gọn.
Sau
đó
biểu
thức
giảm
cho
biểu
thức
của
từ
truờng
nhờ
vào
sự
phân
bố
của
nguồn
khối
trong
bộ
dẫn
khối
không
đồng
nhất.
Điều
này
được
giới
thiệu
ở
phần
cuối
biểu
thức
12.10.
Trong
việc
thiết
kế
thiết
bị
kiểm
tra
từ
sinh
học
chất
lượng
cao,
mục
đích
là
loại
bỏ
tác
dụng
của
nguồn
thứ
cấp
đến
khả
năng
mở
rộng.
Từ
một
ví
dụ
của
biểu
thức
12.6
có
thể
khái
quát
rằng
sự
gián
đoạn
trong
tính
dẫn
là
sự
tương
đương
cới
nguồn
thứ
cấp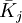 với
với
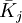 =
=
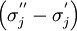
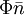 ở
đây
ở
đây
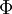 là
tiềm
năng
bề
mặt
trên
là
tiềm
năng
bề
mặt
trên
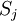 .
Chú
ý
rằng
.
Chú
ý
rằng
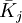 giống
với
nguồn
dòng
thứ
cấp
cho
điện
trường
(biểu
thức
7.10)
như
cho
từ
trường.
giống
với
nguồn
dòng
thứ
cấp
cho
điện
trường
(biểu
thức
7.10)
như
cho
từ
trường.
12.2 Bản chất của nguồn từ sinh học
Biểu thức 12.6 chỉ ra rằng hiện tượng sinh lý cái là nguồn của tin hiệu từ sinh học là hoạt động điện của mô (được mô tả ở trên). Vì thế, với trường hợp, nguồn cho từ tâm đồ (MCG) hoặc từ não đồ (MEG) là họat động điện của cơ tim hoặc tế bào thần kinh, lần lượt là, khi nó là nguồn của điện tâm đồ (ECG) và điện não đồ (EEG). Sự khác nhau về mặt lý thuyết giữa tín hiệu từ sinh học và điện sinh học là sự khác nhau trong việc phân bố độ nhạy của những phép đo này. Sự phân bố độ nhạy ( sự tạo ra trường đạo trình) của phép đo điện được thảo luận chi tiết trong chương trước. Sự phân bố độ nhạy của phép đo từ được bàn chi tiết trong chương này. (những sự khác nhau về kĩ thuật của máy dò điện và từ giới thiệu thêm sự khác nhau. Chúng được bàn một cách ngắn gọn trong phần từ tâm đồ ở chương 20).
Sự khác nhau giữa tin hiệu điện và từ có thể cũng được thấy từ dạng của biểu thức toán học của chúng. Khi so sánh biểu thúc 12.6 và 7.10, chúng ta có thể thấy rằng từ trường xuất phát từ sự xoáy và điện trường xuất phát từ sự phân tán của nguồn. Sự khác nhau này bao gồm cả thành phần thứ nhất vế bên phải của biểu thức được tạo ra từ sự phân bố dòng vào, và thành phần thứ hai được tạo ra từ biên của sự không đồng nhất của nguồn khối.
Nó
được
chỉ
ra
rằng
trong
việc
thiết
kế
đạo
trình
từ
trường
phải
nhớ
đến
nguồn
gốc
điện
của
tín
hiệu
từ
và
dạng
đặc
tính
của
sự
phân
bố
độ
nhạy
của
phép
đo
từ.
Nếu
đạo
trình
của
phép
đo
từ
không
được
thiết
kế
một
cách
cẩn
thận,
thì
có
thể
sự
phân
bố
độ
nhạy
của
đạo
trình
từ
sẽ
giống
với
đạo
trình
điện.
Trong
trường
hợp
đó
phép
đo
từ
trường
sẽ
không
cung
cấp
bất
kì
thông
tin
mới
nào
từ
nguồn
cả.
Xin
chú
ý
rằng
tín
hiệu
từ
sinh
học
được
bàn
ở
trên
được
giả
sử
không
xuất
phát
từ
vật
liệu
từ
bởi
vì
vật
liệu
từ
không
tồn
tại
trong
mô.
Có
những
trường
hợp
đặc
biệt,
tuy
nhiên,
nơi
mà
trường
từ
sinh
học
được
tạo
ra
bởi
vật
liệu
từ
-
ví
dụ,
trong
trường
hợp
tín
hiệu
dựa
vào
vật
liệu
từ
chứa
trong
phổi
của
thợ
hàn
hoặc
sắt
tích
tụ
trong
gan
người
có
bệnh.
Những
trường
hợp
đó
không
được
thảo
luận
ở
cuốn
sách
này.
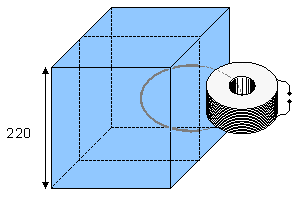
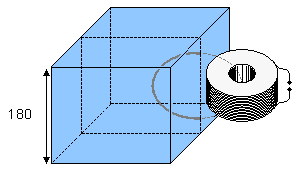
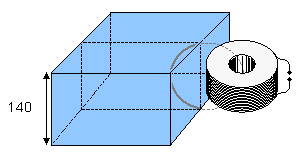
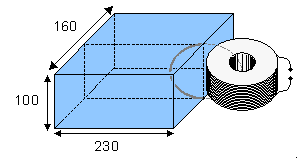
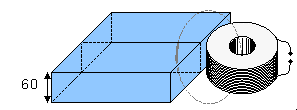
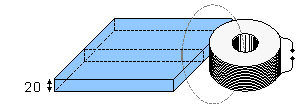
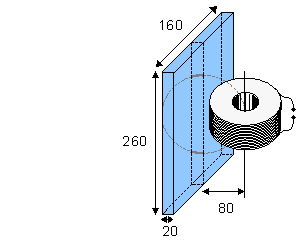
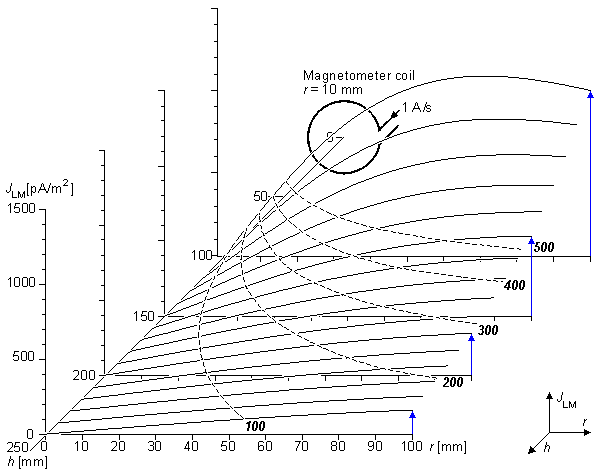
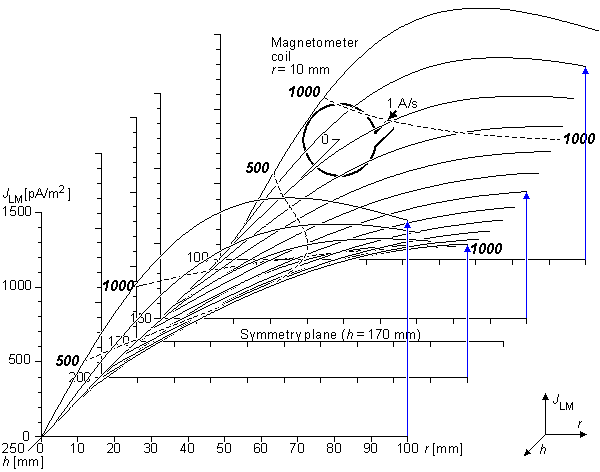
Trường từ sinh học có biên độ rất bé so với trường nhiễu xung quanh và với độ nhạy của đầu dò. Tổng kết các trường được biểu diễn trong hình 12.1 (Malmivuo et al., 1987). Hình này chỉ ra rằng có thể tìm thấy MCG với từ kế cuộn, mặc dù với một tỉ sỗ nhiễu tín hiệu thấp (S/N). Tuy nhiên, hầu hết từ kế cuộn xây dựng cho mục đích từ sinh học (Estola and Malmivuo, 1982) không đủ nhạy để dùng cho MEG sử dụng trong lâm sàng. Vì thế, Superconducting QUantum Interference Device (SQUID) chỉ là thiết bị mà đủ nhạy cho phép đo từ sinh học chất lượng cao. Thiết bị cho trường từ sinh học được đo không được bàn xa hơn trong cuốn sách này.

12.3lý thuyết biến thiên cho từ trường
Điều kiện đầu:
Nguồn:sự
phân
bố
của
yếu
tố
nguồn
dòng
được
đưa
vào
 (nguồn
khối)
(nguồn
khối)
Bộ dẫn: hữu hạn, đồng nhất; hoặc hữu hạn, không đồng nhất với đối xứng trụ
12.3.1 Dạng của trường đạo trình từ
Plonsey đã mở rộng ứng dụng của lý thuyết biến thiên cho điều kiện thời gian thay đổi xảy ra trong phép đo từ sinh học (Plonsey, 1972). Sự phát triển đó tương tự như sự chứng minh của thuyết biến thiên cho điện trường và vì thế không cần lặp lại ở đây. Chỉ biểu thức cho thuyết biên thiên cho phép đo từ là được đề cập. Ở đây, L viết tắt cho “đạo trình”, như trong chương trước, M được viết tắt cho “đạo trình từ” dựa vào dòng biến thiên của đạo hàm theo thời gian.
Dòng
được
nói
trong
một
bộ
dẫn
phụ
thuộc
vào
tốc
độ
của
sự
thay
đổi
của
thông
lượng
từ
mà
kết
nối
với
vòng
lặp
dòng.
Tương
tự
trong
trường
hợp
điện
trường
(
nhìn
biểu
thức
11.30
và
11.52),
các
dòng
được
cấp
điện
biến
thiên
(thay
đổ
theo
thời
gian)
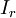 được
chuẩn
hóa
để
đạo
hàm
theo
thời
gian
của
nó
thống
nhất
cho
tất
cả
các
giá
trị
được
chuẩn
hóa
để
đạo
hàm
theo
thời
gian
của
nó
thống
nhất
cho
tất
cả
các
giá
trị
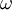 .
Phương
trình
cần
thiết
cho
lý
thuyết
trường
đạo
trình
cho
phép
đo
từ
sinh
học
sau
đó
có
thể
đạt
được
một
cách
dễ
dàng
từ
phương
trình
tương
ứng
trong
các
phép
đo
điện.
.
Phương
trình
cần
thiết
cho
lý
thuyết
trường
đạo
trình
cho
phép
đo
từ
sinh
học
sau
đó
có
thể
đạt
được
một
cách
dễ
dàng
từ
phương
trình
tương
ứng
trong
các
phép
đo
điện.
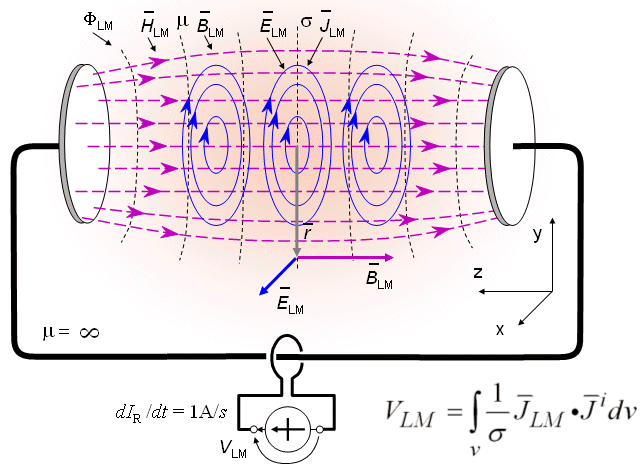
Sóng điện tâm lưỡng cực cơ bản trong phép đo từ tính là một ống dây (cuộn dây) với một lõi và phần cuối tròn phẳng có độ từ thẩm xác định, như được biểu diễn trong hình 12.2. Nếu cuộn dây được cung cấp điện với một dòng điện , một từ trường được tạo ra, nó có thể được xem như là kết quả từ sự tích từ (bằng và đối) tại cuối của cuộn dây. Những chỗ cuối này được gọi là từ cực (Baule and McFee, 1963). ( từ “điện cực được giới thiệu bởi Michael Faraday(1834).) Độ dẫn từ lưỡng cực cơ bản này là tương đương với độ dẫn điện lưỡng cực cơ bản được trình bày trong hình 11.23.
Khi
dòng
biến
thiên
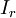 được
đưa
vào
đạo
trình
từ
cơ
bản,
nó
tạo
ra
trong
một
không
gian
xác
định
của
độ
từ
thẩm
giống
nhau
một
trường
thế
từ
vô
hướng
được
đưa
vào
đạo
trình
từ
cơ
bản,
nó
tạo
ra
trong
một
không
gian
xác
định
của
độ
từ
thẩm
giống
nhau
một
trường
thế
từ
vô
hướng
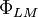 của
trạng
thái
không
gian
khác
nhau
như
trường
thế
điện
vô
hướng
của
trạng
thái
không
gian
khác
nhau
như
trường
thế
điện
vô
hướng
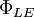 trong
một
môi
trường
vô
hạn
các
độ
dẫn
thống
nhất
phát
sinh
từ
đạo
trình
điện
được
đưa
điện
vào
một
cách
biến
thiên,
điện
cực
của
nó
được
đặt
ở
phía
tương
ứng
với
từ
cực.
Như
chú
ý
trong
phần
11.6.6
,
nếu
điện
cực
hoặc
từ
cực
được
đặt
song
song
và
kích
thứớc
của
chúng
rộng
so
với
sự
phân
chia
của
chúng,
thì
cả
trong
một
môi
trường
vô
hạn
các
độ
dẫn
thống
nhất
phát
sinh
từ
đạo
trình
điện
được
đưa
điện
vào
một
cách
biến
thiên,
điện
cực
của
nó
được
đặt
ở
phía
tương
ứng
với
từ
cực.
Như
chú
ý
trong
phần
11.6.6
,
nếu
điện
cực
hoặc
từ
cực
được
đặt
song
song
và
kích
thứớc
của
chúng
rộng
so
với
sự
phân
chia
của
chúng,
thì
cả
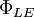 và
và
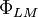 là
giống
nhau
trong
vùng
trung
tâm.
là
giống
nhau
trong
vùng
trung
tâm.
ở đây:
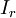 =
dòng
điện
biến
thiên
=
dòng
điện
biến
thiên
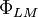 =
trường
thế
từ
vô
hướng
=
trường
thế
từ
vô
hướng
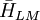 =
từ
trường
biến
thiên
=
từ
trường
biến
thiên
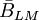 =
cảm
ứng
từ
biến
thiên
=
cảm
ứng
từ
biến
thiên
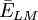 =
điện
trường
biến
thiên
=
điện
trường
biến
thiên
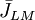 =
trường
đạo
trình
=
trường
đạo
trình
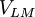 =
điện
thế
trong
trường
đạo
trình
nhờ
vào
nguồn
khối
=
điện
thế
trong
trường
đạo
trình
nhờ
vào
nguồn
khối
 trong
bộ
dẫn
khối
trong
bộ
dẫn
khối
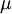 =
độ
từ
thẩm
của
môi
trường
=
độ
từ
thẩm
của
môi
trường
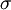 =
độ
dẫn
cửa
môi
trường
=
độ
dẫn
cửa
môi
trường
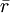 =
vector
bán
kính
=
vector
bán
kính
Một môi trường đồng nhất không giới hạn được yêu cầu cho độ dẫn là gấp đôi cho độ thấm từ, nơi mà điểm cuối cùng là đồng nhất trong cơ thể và không gian. Như trong các phép đo điện, có thể để tạo ra sự kết hợp đạo trình từ bằng cách kết nối bất kì số nào của đầu dò với nhau.
Bây
giờ
chúng
ta
khảo
sát
bản
chất
của
trường
đạo
trình
từ
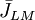 được
tạo
ra
bởi
sự
đưa
vào
dòng
điện
biên
thiên
của
cuộn
dây
của
đầu
dò
từ
với
một
dòng
được
tạo
ra
bởi
sự
đưa
vào
dòng
điện
biên
thiên
của
cuộn
dây
của
đầu
dò
từ
với
một
dòng
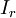 Ir
tại
một
tần
số
góc.
Sử
dụng
định
chuẩn
kí
hiệu
giống
nhau
giữa
dòng
điện
được
đưa
vào
và
điện
thế
được
đo
như
trong
trường
hợp
điện,
hình
11.23,
chúng
ta
thu
được
tình
huống
tương
ứng
với
phép
đo
từ,
như
trong
hình
12.2.
Ir
tại
một
tần
số
góc.
Sử
dụng
định
chuẩn
kí
hiệu
giống
nhau
giữa
dòng
điện
được
đưa
vào
và
điện
thế
được
đo
như
trong
trường
hợp
điện,
hình
11.23,
chúng
ta
thu
được
tình
huống
tương
ứng
với
phép
đo
từ,
như
trong
hình
12.2.
Trường
từ
biến
thiên
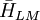 xuất
phát
từ
xuất
phát
từ
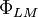 có
dạng
sau:
có
dạng
sau:
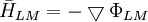 (12.07)
(12.07)
Cảm
ứng
từ
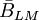 là
là
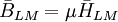 (12.08)
(12.08)
ở
đây
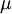 là
độ
từ
thẩm
của
môi
trường.
Giả
sử
là
độ
từ
thẩm
của
môi
trường.
Giả
sử
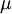 là
cố
định,
phản
xạ
lại
trường
hợp
không
được
giả
sử
của
vật
liệu
từ
rời
rạc.
là
cố
định,
phản
xạ
lại
trường
hợp
không
được
giả
sử
của
vật
liệu
từ
rời
rạc.
Cường
độ
điện
trường
biến
thiên
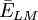 xuất
phát
từ
cảm
ứng
từ
biến
thiên
xuất
phát
từ
cảm
ứng
từ
biến
thiên
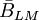 (gây
ra
từ
cuộn
dây
có
dòng
điện
chạy
qua)
phụ
thuộc
vào
hệ
đạo
trình
khối
và
trường.
Với
từ
trường
là
đối
xứng
trục
và
đồng
nhất
với
một
số
vùng
được
giới
hạn
(trường
hợp
đối
xứng
trụ),
(gây
ra
từ
cuộn
dây
có
dòng
điện
chạy
qua)
phụ
thuộc
vào
hệ
đạo
trình
khối
và
trường.
Với
từ
trường
là
đối
xứng
trục
và
đồng
nhất
với
một
số
vùng
được
giới
hạn
(trường
hợp
đối
xứng
trụ),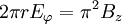 với
vùng
này
(
với
vùng
này
(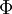 và
z
đang
ở
trong
hệ
tọa
độ
trụ),
hoặc
trong
kí
hiệu
vector:
và
z
đang
ở
trong
hệ
tọa
độ
trụ),
hoặc
trong
kí
hiệu
vector:
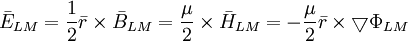 (12.9)
(12.9)
Trong
biểu
thức
này
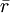 là
vector
bán
kính
trong
hệ
tọa
độ
trụ
được
đo
từ
trục
đối
xứng
(z)
như
gốc.
Như
trước,
điều
kiện
điều
hòa
được
giả
sử
để
tất
cả
số
lượng
trường
là
vector
pha
phức
tạp.
Hơn
nữa,
như
đã
chú
ý
trước
đó,
là
vector
bán
kính
trong
hệ
tọa
độ
trụ
được
đo
từ
trục
đối
xứng
(z)
như
gốc.
Như
trước,
điều
kiện
điều
hòa
được
giả
sử
để
tất
cả
số
lượng
trường
là
vector
pha
phức
tạp.
Hơn
nữa,
như
đã
chú
ý
trước
đó,
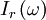 được
điều
chỉnh
để
đại
lượng
của
được
điều
chỉnh
để
đại
lượng
của
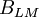 là
độc
lập
với
là
độc
lập
với
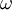 .
Sự
dịch
pha
90
độ
của
điện
trường
liên
quan
đến
từ
trường,
được
giả
sử
là
được
chứa
trong
vector
pha
điện
trường.
Những
giả
thiết
về
trường
đứợc
giả
sử
ở
trên
nên
là
một
sự
xấp
xỉ
hợp
lý
với
trường
biến
thiên
thực
tế
được
thiết
lập
bởi
đầu
dò
từ
trường.
.
Sự
dịch
pha
90
độ
của
điện
trường
liên
quan
đến
từ
trường,
được
giả
sử
là
được
chứa
trong
vector
pha
điện
trường.
Những
giả
thiết
về
trường
đứợc
giả
sử
ở
trên
nên
là
một
sự
xấp
xỉ
hợp
lý
với
trường
biến
thiên
thực
tế
được
thiết
lập
bởi
đầu
dò
từ
trường.
Kết
quả
trong
biểu
thức
12.9
tương
ứng
với
cường
độ
điện
trường
biến
thiên
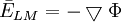 được
tạo
ra
bởi
dòng
biến
thiên
của
đạo
trình
điện
(được
mô
tả
trong
biểu
thức
11.53
trong
chương
trước)
được
tạo
ra
bởi
dòng
biến
thiên
của
đạo
trình
điện
(được
mô
tả
trong
biểu
thức
11.53
trong
chương
trước)
Mật độ dòng từ trường đạo trình có thể được tính từ công thức 12.9. vì thế:
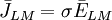 (12.10)
(12.10)
Chúng
ta
thu
được
cho
trường
đạo
trình
từ
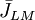
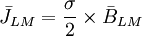 (12.11)
(12.11)
Trường
đạo
trình
từ
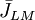 có
các
thuộc
tính
sau:
có
các
thuộc
tính
sau:
1.Mật
độ
dòng
trường
đạo
trình
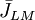 ở
mọi
nơi
xoay
quanh
và
đồng
tâm
với
trục
đối
xứng.
ở
mọi
nơi
xoay
quanh
và
đồng
tâm
với
trục
đối
xứng.
2.Độ
lớn
của
mật
độ
dòng
trường
đạo
trình
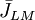 tỉ
lệ
thuận
với
khoảng
cách
từ
trục
đối
xứng
r
(đủ
để
các
điểm
trường
vẫn
còn
trong
trường
tỉ
lệ
thuận
với
khoảng
cách
từ
trục
đối
xứng
r
(đủ
để
các
điểm
trường
vẫn
còn
trong
trường
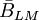 đồng
nhất)
đồng
nhất)
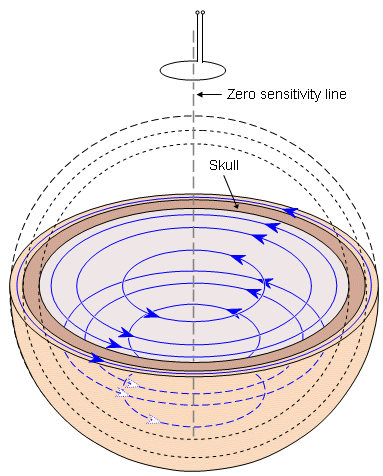
3. Như một hệ quả của (2), độ nhạy là 0 tại trục đối xứng. Vì thế, trục đối xứng được gọi là đường độ nhạy bằng 0.
Dựa
trên
biểu
thức
11.30
và
chú
ý
rằng
cũng
trong
trường
hợp
từ
dong
biến
thiên
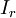 được
chuẩn
hóa
để
nó
thống
nhất
với
tất
cả
giá
trị
được
chuẩn
hóa
để
nó
thống
nhất
với
tất
cả
giá
trị
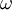 ,
chúng
ta
cân
bằng
điện
thế
,
chúng
ta
cân
bằng
điện
thế
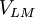 trong
đạo
trình
từ
được
tạo
ra
bởi
một
mật
độ
moment
lưỡng
cực
dòng
trong
đạo
trình
từ
được
tạo
ra
bởi
một
mật
độ
moment
lưỡng
cực
dòng
 như
(Plonsey.
1972)
như
(Plonsey.
1972)
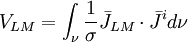 (12.12)
(12.12)
Biểu
thức
này
giống
với
biểu
thức
11.30,
mô
tả
sự
phân
bố
độ
nhạy
của
đạo
trình
điện.
Sự
phân
bố
độ
nhạy
của
phép
đo
từ
là
điểm
khác
nhau
từ
phép
đo
điện
vì
trường
đạo
trình
từ
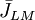 có
dạng
khác
trường
đạo
trình
điện
có
dạng
khác
trường
đạo
trình
điện
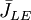 .
.
Trong
vật
liệu
ở
trên,
chúng
ta
giả
sử
rằng
môi
trường
đạo
trình
là
đồng
nhất
và
hữu
hạn.
Việc
thảo
luận
này
cũng
bao
gồm
môi
trường
đạo
trình
hình
trụ
đồng
nhất
của
bán
kính
xác
định
nếu
từ
trường
có
dòng
biến
thiên
chạy
qua
là
đồng
nhất
và
trong
hướng
của
trục
đối
xứng.
bởi
vì
hướng
đồng
tâm
của
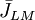 trong
trường
hợp
không
có
được
giới
hạn
không
bị
can
thiệp
khi
đường
bao
hình
trụ
xác
định
được
giới
thiệu.
Như
trong
trường
hợp
môi
trường
xác
định,
độ
lớn
dòng
trường
đạo
trình
tỉ
lệ
thuận
với
khoảng
cách
r
từ
trục
đối
xứng.
Trên
trục
đối
xứng,
mật
độ
dòng
trường
đạo
trình
là
bằng
0,
và
vì
thế,
nó
được
gọi
là
đường
có
độ
nhạy
bằng
0
(Eskola,
1983;
Eskola
and
Malmivuo,
1983).
trong
trường
hợp
không
có
được
giới
hạn
không
bị
can
thiệp
khi
đường
bao
hình
trụ
xác
định
được
giới
thiệu.
Như
trong
trường
hợp
môi
trường
xác
định,
độ
lớn
dòng
trường
đạo
trình
tỉ
lệ
thuận
với
khoảng
cách
r
từ
trục
đối
xứng.
Trên
trục
đối
xứng,
mật
độ
dòng
trường
đạo
trình
là
bằng
0,
và
vì
thế,
nó
được
gọi
là
đường
có
độ
nhạy
bằng
0
(Eskola,
1983;
Eskola
and
Malmivuo,
1983).
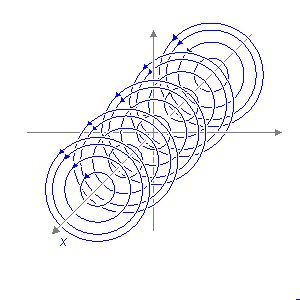
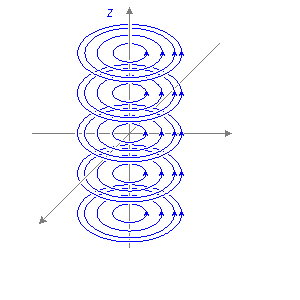
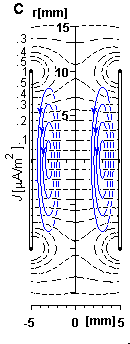
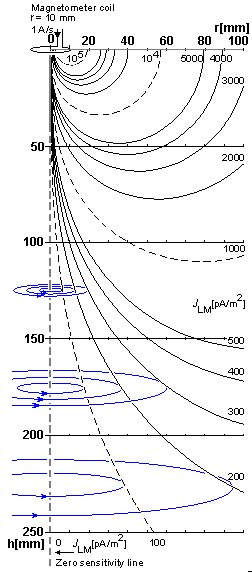
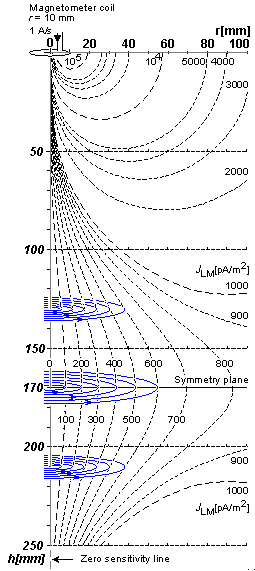
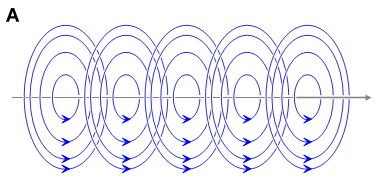
Dạng
của
trường
đạo
trình
từ
được
trình
bày
chi
tiết
trong
hình
12.3.
Để
so
sánh,
trường
đạo
trình
từ
được
trình
bày
trong
hình
với
bốn
cách
khác
nhau.
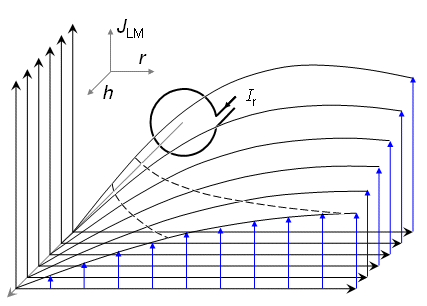
Hình
12.3A
chỉ
ra
mật
độ
dòng
trường
đạo
trình
từ
trong
dạng
phối
cảnh
ba
chiều
với
đường
sức
trường
đạo
trình
được
định
hướng
một
cách
tiếp
tuyến
xung
quang
trục
đối
xứng.
Như
chú
ý
trước,
bởi
vì
mật
độ
dòng
trường
đạo
trình
tỉ
lệ
thuận
với
khoảng
cách
r
từ
trục
đối
xứng,
trục
đối
xứng
tại
thời
điểm
này
là
dường
có
độ
nhạy
bằng
0.
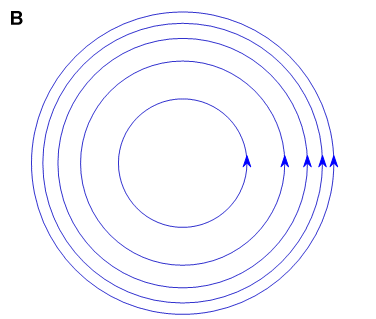
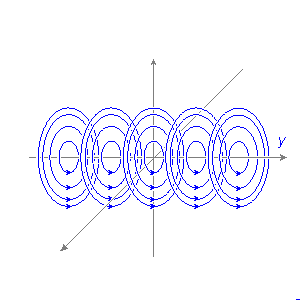
Hình
12.3B
chỉ
ra
dạng
của
trường
đạo
trình
trong
một
mặt
phẳng
vuông
góc
với
trục.
Những
đường
sức
thường
được
vẽ
để
số
lượng
không
đổi
của
dòng
được
giả
sử
chảy
giữa
hai
đường
sức.
Vì
thế,
mật
độ
đường
sức
tỉ
lệ
thuận
với
mật
độ
dòng.
(trong
trường
hợp
này
dòng
trường
đạo
trình
có
một
thành
phần
bình
thường
với
mặt
phẳng
của
hình
minh
họa,
các
đường
sức
là
không
liên
tục,
và
một
số
không
chính
xác
được
đưa
vào
hình
minh
họa,
như
có
thể
được
thấy
trong
phần
13.4).
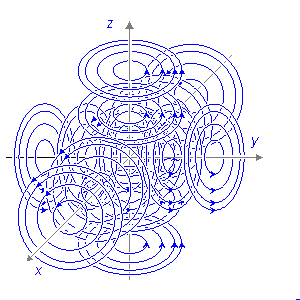
Hình
12.3C
minh
họa
trường
đạo
trình
với
vector
mật
độ
dòng,
được
đặt
tại
góc
của
lưới
đều.
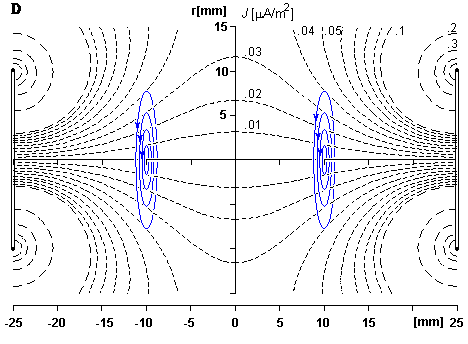
Cuối
cùng,
hình
12.3D
chỉ
ra
độ
lớn
của
mật
độ
dòng
trường
đạo
trình
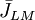 như
một
hàm
của
khoảng
cách
r
với
trục
đối
xứng
với
khoảng
cách
từ
từ
kế
h
như
một
tham
số.
Hình
minh
họa
này
không
chỉ
ra
hướng
của
mật
độ
dòng
trường
đạo
trình,
nhưng
nó
được
biết
là
có
hướng
tiếp
tuyến.
Trong
hình
12.3E
những
đường
nét
đứt
tham
gia
vào
điểm
nơi
mà
mật
độ
dòng
trường
đạo
trình
có
giá
trị
như
nhau,
vì
thế
chúng
được
gọi
là
những
đường
đẳng
nhạy.
như
một
hàm
của
khoảng
cách
r
với
trục
đối
xứng
với
khoảng
cách
từ
từ
kế
h
như
một
tham
số.
Hình
minh
họa
này
không
chỉ
ra
hướng
của
mật
độ
dòng
trường
đạo
trình,
nhưng
nó
được
biết
là
có
hướng
tiếp
tuyến.
Trong
hình
12.3E
những
đường
nét
đứt
tham
gia
vào
điểm
nơi
mà
mật
độ
dòng
trường
đạo
trình
có
giá
trị
như
nhau,
vì
thế
chúng
được
gọi
là
những
đường
đẳng
nhạy.
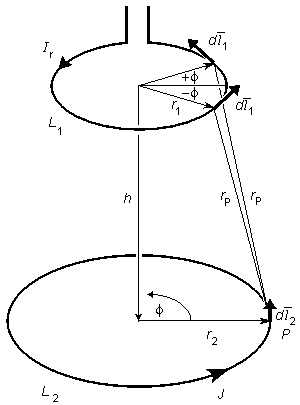
Những
hướng
liên
quan
của
từ
trường
và
dòng
được
đưa
vào
và
tín
hiệu
được
dò
tìm
được
phác
họa
trong
hình
12.2.
Nếu
cảm
ứng
từ
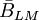 của
biểu
thức
12.11
là
đồng
nhất
và
nằm
trong
hướng
tọa
độ
âm,
như
trong
hình
12.2,
dạng
của
kết
quả
mật
độ
dòng
trường
đạo
trình
của
biểu
thức
12.11
là
đồng
nhất
và
nằm
trong
hướng
tọa
độ
âm,
như
trong
hình
12.2,
dạng
của
kết
quả
mật
độ
dòng
trường
đạo
trình
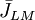 là
tiếp
tuyến
và
được
định
hướng
trên
hướng
dương
của
vòn
tròn.
Nên
nhớ
rằng,
điều
kiện
điều
hòa
đã
từng
được
giả
sử
để
vì
thể
chúng
ta
đang
vẽ
đồ
thị
độ
lớn
đỉnh
của
là
tiếp
tuyến
và
được
định
hướng
trên
hướng
dương
của
vòn
tròn.
Nên
nhớ
rằng,
điều
kiện
điều
hòa
đã
từng
được
giả
sử
để
vì
thể
chúng
ta
đang
vẽ
đồ
thị
độ
lớn
đỉnh
của
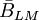 đối
với
đối
với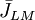 ,
sự
chọn
lựa
kí
hiệu
cho
mỗi
lớp
vector
là
chủ
quan.
Mối
quan
hệ
tức
thời
có
thể
được
tìm
thấy
từ
biểu
thức
12.11,
nếu
kí
hiệu
vector
pha
rõ
ràng
được
quay
trở
lại,
bao
gồm
độ
lệch
pha
90
,
sự
chọn
lựa
kí
hiệu
cho
mỗi
lớp
vector
là
chủ
quan.
Mối
quan
hệ
tức
thời
có
thể
được
tìm
thấy
từ
biểu
thức
12.11,
nếu
kí
hiệu
vector
pha
rõ
ràng
được
quay
trở
lại,
bao
gồm
độ
lệch
pha
90 của
của
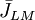 .
.
12.3.2Nguồn của từ trường
Phần
này
cung
cấp
một
sự
mô
tả
lần
lượt
nguồn
của
từ
trường
được
cảm
nhận
bởi
cuộn
dây
đặt
trong
từ
trường
(giống
với
trường
hợp
trục
đối
xứng).
Bằng
việc
thay
biểu
thức
12.9
vào
biểu
thức
12.10,
và
sau
đó
biểu
thức
này
vào
12.12,
chúng
ta
thu
được
(
chú
ý
rằng
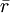 trong
hệ
tọa
độ
trụ)
trong
hệ
tọa
độ
trụ)
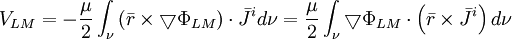 (12.13)
(12.13)
Sử
dụng
vector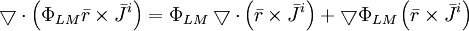 ,
thu
được
dạng
của
biểu
thức
12.3
,
thu
được
dạng
của
biểu
thức
12.3
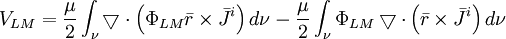 (12.14)
(12.14)
Áp
dụng
lý
thuyết
phân
chia
cho
số
hạng
đầu
tiên
bên
phải
và
sử
dụng
một
vector
mở
rộng
(i.e.,
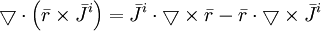 )
vào
số
hạng
thứ
hai
của
biểu
thức
12.4,
và
chú
ý
rằng
)
vào
số
hạng
thứ
hai
của
biểu
thức
12.4,
và
chú
ý
rằng
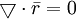 ,
ta
thu
được
,
ta
thu
được
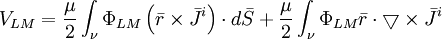 (12.15)
(12.15)
Vì
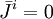 tại
cận
của
không
gian,
bề
mặt
tích
chập
bằng
0,
nên
ta
có
tại
cận
của
không
gian,
bề
mặt
tích
chập
bằng
0,
nên
ta
có
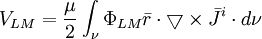 (12.16)
(12.16)
Biểu
thức
này
tương
ứng
với
biểu
thức
11.50
trong
phép
đo
điện.
Số
lượng
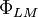 là
thế
từ
vô
hướng
trong
bộ
dẫn
khối
nhờ
vào
dòng
biến
thiên
được
đưa
vào
của
pickup
lead.
Số
hạng
là
thế
từ
vô
hướng
trong
bộ
dẫn
khối
nhờ
vào
dòng
biến
thiên
được
đưa
vào
của
pickup
lead.
Số
hạng
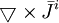 được
định
nghĩa
như
nguồn
xoáy,
được
định
nghĩa
như
nguồn
xoáy,
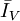 :
:
 (12.17)
(12.17)Trong biểu thức 12.16 đây là độ lớn của nguồn từ trường.
Sự thiết kế nguồn xoáy cho nguồn này diễn ra như là kết quả của việc định nghĩa sự xoáy(curl). Cuối cùng là sự khép kín trên mỗi vùng đơn vị, đó là:
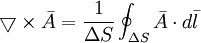 (12.18)
(12.18)
Và
tích
phân
đường
được
lấy
xung
quanh
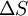 tại
tất
cả
các
điểm
trên
vùng
quan
tâm
để
nó
được
định
hướng
trong
trường
để
làm
lớn
nhất
tích
phân
(cái
mà
tạo
ra
hướng
của
vòng
xoáy).
tại
tất
cả
các
điểm
trên
vùng
quan
tâm
để
nó
được
định
hướng
trong
trường
để
làm
lớn
nhất
tích
phân
(cái
mà
tạo
ra
hướng
của
vòng
xoáy).
Nếu quan tâm đến trường vận tốc được kết hợp với một lượng nước trong một bình chứa, sau đó lưu lượng nguồn của nó phải bằng 0 nếu nước không được thêm vào hoặc lấy ra. Nhưng với trường, không cần thiết phải bằng 0 trong trường hợp không có nguồn lưu lượng bởi vì nước có thể được khuấy lên., do đó tạo ra trường khác 0. Nhưng xoáy do đó được tạo ra dẫn tới một curl khác 0 đến khi có sự tồn tại rõ ràng một ồng khép kín. Điều này giải thích cách sử dụng thuật ngữ “vortex” cũng như vai trò quan trọng của nó như là nguồn của một trường độc lập của lưu lượng.
12.3.3 tổng kết các biểu thức lý thuyết trường đạo trình cho phép đo điện và từ
Như
được
tổng
kết
trong
hình
12.2,
như
một
kết
quả
của
dòng
biến
thiên
được
đưa
vào
của
từ
trường,
năm
trường
biến
thiên
sau
được
tạo
ra
trong
bộ
dẫn
khối:
trường
thế
từ
vô
hướng
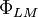 (được
minh
họa
với
bề
mặt
đẳng
thế),
từ
trường
(được
minh
họa
với
bề
mặt
đẳng
thế),
từ
trường
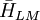 (được
minh
họa
với
dòng
trường),
cảm
ứng
từ
(được
minh
họa
với
dòng
trường),
cảm
ứng
từ
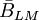 (được
minh
họa
với
đường
thông
lượng),
điện
trường
(được
minh
họa
với
đường
thông
lượng),
điện
trường
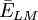 (được
minh
họa
bởi
các
dòng
trường),
và
trường
dòng
điện
(được
minh
họa
bởi
các
dòng
trường),
và
trường
dòng
điện
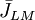 (được
mô
tả
với
thông
lượng
dòng
và
được
gọi
là
trường
đạo
trình).
(được
mô
tả
với
thông
lượng
dòng
và
được
gọi
là
trường
đạo
trình).
Ngoài năm trường này chúng ta có thể định nghĩa thêm một trường thứ sáu đó là mặt phẳng đẳng nhạy. Nó được định nghĩa tương tự như đạo trình điện trong phần 11.6.6. Khi độ từ thẩm là đẳng hướng (thường là trong mô sinh học), đường từ trường trùng với thông lượng cảm ứng từ. Khi bộ dẫn là đẳng hướng, dòng điện trường trùng với thông lượng dòng. Vì thế trong phần tóm tắt, trong một hệ thống đạo trình dò tìm moment lưỡng cực từ của một nguồn khối (xem phần 12.6) từ sáu trường đã nói ở trên, dòng từ trường trùng với thông lượng từ và dòng điện trường trùng với thông lượng trường đạo trình. Tương tự như trong trường hợp điện (xem phần 12.6), mặt phẳng đẳng thế từ vô hướng trùng với từ đẳng trường và mặt phẳng đẳng thông.
Bảng 12.1 tóm tắt biểu thức lý thuyết trường đạo trình cho phép đo điện và từ.
Sự
phụ
thuộc
không
gian
của
thế
điện
và
từ
vô
hướng
được
tìm
thấy
ở
biểu
thức
của
Laplace.
Những
trường
này
sẽ
có
những
dạng
giống
nhau
(
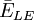 vs.
vs.
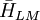 ),
nếu
hình
dạng
và
vị
trí
của
điện
cực
và
từ
cực
là
như
nhau
và
nếu
không
có
hiệu
ứng
của
bộ
dẫn
khối
không
đồng
nhất
hoặc
phân
cách
với
không
khí.
Tương
tự,
biểu
thức
cho
tín
hiệu
điện
và
từ
),
nếu
hình
dạng
và
vị
trí
của
điện
cực
và
từ
cực
là
như
nhau
và
nếu
không
có
hiệu
ứng
của
bộ
dẫn
khối
không
đồng
nhất
hoặc
phân
cách
với
không
khí.
Tương
tự,
biểu
thức
cho
tín
hiệu
điện
và
từ
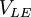 and
and
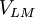 ,
khi
tích
phân
của
tích
vô
hướng
của
trường
đạo
trình
và
trường
mật
độ
dòng
được
đưa
vào,
có
dạng
như
nhau.
,
khi
tích
phân
của
tích
vô
hướng
của
trường
đạo
trình
và
trường
mật
độ
dòng
được
đưa
vào,
có
dạng
như
nhau.
Điểm
khác
nhau
trong
việc
phân
chia
độ
nhạy
của
việc
dò
tim
điện
và
trường
của
mật
độ
dòng
được
đưa
vào
 là
kết
quả
của
sự
khác
nhau
về
dạng
của
trường
đạo
trình
điện
và
từ
là
kết
quả
của
sự
khác
nhau
về
dạng
của
trường
đạo
trình
điện
và
từ
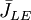 và
và
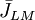 .
Dạng
thứ
nhất
có
dạng
của
điện
trường
biến
thiên,
trong
khi
dạng
thứ
hai
là
dạng
xoáy
của
từ
trường
biến
thiên.
.
Dạng
thứ
nhất
có
dạng
của
điện
trường
biến
thiên,
trong
khi
dạng
thứ
hai
là
dạng
xoáy
của
từ
trường
biến
thiên.
Chúng ta nhấn mạnh lần nữa rằng sự thảo luận này của từ trường được giới hạn cho trường hợp đối xứng trục và điều kiện đồng nhất ( những điều kiện được mong đợi cho những khả năng ứng dụng được )
Bảng 12.1 Những phương trình cho điện trường và từ trường
| Đại lượng | Điện trường | Từ trường |
| Trường như một gradient âm của thế vô hướng của dòng đưa vào biến thiên |
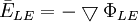 (11.53)
(11.53) |
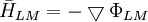 (12.7) (12.7) |
| Cảm ứng từ do dòng điện đưa vào biến thiên |
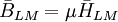 (12.8) (12.8) |
|
| Điện trường biến thiên*) |
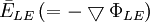 (11.53)
(11.53) |
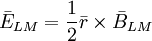 (12.9)
(12.9) |
| Trường đạo trình( trường dòng) |
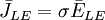 (11.54)
(11.54) |
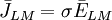 (12.10)
(12.10) |
Tín
hiệu
dò
được
khi: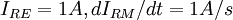 |
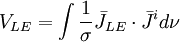 (11.30)
(11.30) |
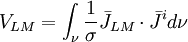 (12.12)
(12.12) |
*)chú ý: điểm khác nhau quan trọng giữa trường đạo trình điện và từ được giải thích như sau: điện trường biến thiên của gradient âm của thế điện vô hướng (như được giải thích trong dòng đầu tiên của bảng). Điện trường biến thiên của đạo trình từ có dạng xoáy của gradient âm của thế từ vô hướng. (trong cả hai trường hợp, trường đạo trình, được định nghĩa như trường dòng, thu được từ điện trường biến thiên bởi phép nhân với bộ dẫn.) Số lượng của dấu ngoặc là sô lượng biểu thức trong bảng.
12.4 Moment lưỡng cực từ của nguồn khối
Điều kiện đầu:
Nguồn:
sự
phân
bố
của
 tạo
ra
một
nguồn
khối
tạo
ra
một
nguồn
khối
Bộ dẫn: hữu hạn, không đồng nhất
Moment
lưỡng
cực
từ
của
sự
phân
bố
dòng
khối
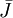 liên
quan
tới
nguồn
bất
kì
được
định
nghĩa
như
(Stratton,
1941):
liên
quan
tới
nguồn
bất
kì
được
định
nghĩa
như
(Stratton,
1941):
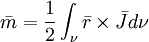 (12.19)
(12.19)
ở
đây
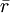 là
vector
bán
kính
tính
từ
gốc.
Mô
moment
lưỡng
cực
từ
của
mật
đồ
dòng
tổng
là
vector
bán
kính
tính
từ
gốc.
Mô
moment
lưỡng
cực
từ
của
mật
đồ
dòng
tổng
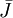 ,
mà
nó
bao
gồm
một
nguồn
dòng
khối
được
phân
chia
,
mà
nó
bao
gồm
một
nguồn
dòng
khối
được
phân
chia
 và
dòng
đạo
trình
của
nó,
và
dòng
đạo
trình
của
nó,
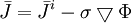 (7.2)
(7.2)Suy ra
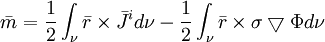 (12.20)
(12.20)
Giả
sử
σ
là
cố
định,
chúng
ta
có
thể
sử
dụng
vector
riêng
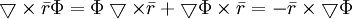 (vì
(vì
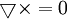 ),
và
đổi
số
hạng
thứ
hai
bên
phải
của
biểu
thức
12.20
thành
dạng :
),
và
đổi
số
hạng
thứ
hai
bên
phải
của
biểu
thức
12.20
thành
dạng :
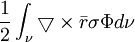 (12.21)
(12.21)
Bây
giờ
chúng
ta
áp
dụng
12.4
vào
12.21
và
chú
ý
rằng
volume
và
vì
thế
tích
phân
mặt
phải
được
tính
từng
đọng
cho
mỗi
vùng
nơi
mà
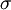 có
giá
trị
khác
nhau.
Tổng
của
các
tích
phân
và
chỉ
ra
các
giá
trị
của
dộ
dẫn
có
giá
trị
khác
nhau.
Tổng
của
các
tích
phân
và
chỉ
ra
các
giá
trị
của
dộ
dẫn
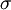 với
primed
and
double-primed
kí
hiệu
của
mỗi
cận,
cuối
cùng
từ
biểu
thức
12.20
ta
thu
được
với
primed
and
double-primed
kí
hiệu
của
mỗi
cận,
cuối
cùng
từ
biểu
thức
12.20
ta
thu
được
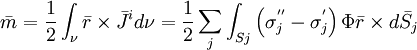 (12.22)
(12.22)
Biểu
thức
này
đưa
đến
moment
lưỡng
cực
từ
của
nguồn
khối
 được
đặt
trong
bộ
dẫn
khối
không
đồng
nhất
xác
định.
Như
trong
biểu
thức
12.6,
số
hạng
thứ
nhất
ở
vế
phải
biểu
thức
12.22
biểu
diễn
thành
phần
nguồn
khối,
và
số
hạng
thứ
hai
là
thành
phần
của
đường
bao
giữa
những
vùng
khác
nhau
của
bộ
dẫn.
Biểu
thức
này
đựơc
tìm
ra
lần
đầu
tiên
bởi
David
Geselowitz
(Geselowitz,
1970).
được
đặt
trong
bộ
dẫn
khối
không
đồng
nhất
xác
định.
Như
trong
biểu
thức
12.6,
số
hạng
thứ
nhất
ở
vế
phải
biểu
thức
12.22
biểu
diễn
thành
phần
nguồn
khối,
và
số
hạng
thứ
hai
là
thành
phần
của
đường
bao
giữa
những
vùng
khác
nhau
của
bộ
dẫn.
Biểu
thức
này
đựơc
tìm
ra
lần
đầu
tiên
bởi
David
Geselowitz
(Geselowitz,
1970).
12.5 Trường đạo trình lý tưởng của một đầu dò đạo trình lưỡng cực từ tương đương của nguồn khối
Điều kiện đầu:
Nguồn:
Sự
phân
bố
của
 tạo
ra
nguồn
khối
(tại
gốc)
tạo
ra
nguồn
khối
(tại
gốc)
Bộ dẫn: hữu hạn (hoặc hình cầu) đồng nhất
Phần này phát triển dạng của trường đạo trình cho một máy dò dò tìm moment lưỡng cực từ tương đương của nguồn khối đã phân chia được đặt trong một bộ dẫn khối đồng nhất hữu hạn (hoặc hình cầu). Đầu tiên chúng ta phải chọn điểm gốc; chúng ta chọn trung tâm của nguồn làm gốc. (sự lựa chọn này là cần thiết, bởi nhân tố r trong biểu thức của moment lưỡng cực từ, biểu thức 12.22)
Tổng moment lưỡng cực từ của nguồn khối được cân bằng trong biểu thức 12.20 như tích phân khối. Chúng ta chú ý rằng hàm mật độ moment lưỡng cực từ được lấy từ tích phân
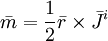 (12.23)
(12.23)
Biểu
thức
12.14
cung
cấp
mối
quan
hệ
giữa
điện
thế
đạo
trình
(từ)
và
sự
phân
bố
nguồn
dòng
 ,
có
dạng
,
có
dạng
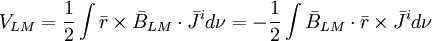 (12.24)
(12.24)Thế biểu thức 12.23 vào biểu thức 12.24 thu được mối quan hệ mong muốn giữa điện thế đạo trình và mật độ moment lưỡng cực từ, cụ thể là
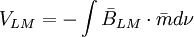 (12.25)
(12.25)Biểu thức này có thể được thể hiện trong các từ như sau:
1.
Một
thành
phần
của
moment
từ
lưỡng
cực
của
nguồn
khối
được
lấy
với
một
đầu
dò,
khi
có
dòng
điện
chạy
qua,
tạo
ra
một
từ
từ
trường
biến
thiên
đồng
nhất
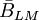 trong
phần
âm
của
hệ
tọa
độ
trong
phạm
vi
của
nguồn
khối.
trong
phần
âm
của
hệ
tọa
độ
trong
phạm
vi
của
nguồn
khối.
2.
Từ
trường
biển
thiên
tạo
ra
một
điện
trường
biến
thiên
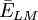 =
=
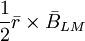 và
trường
đạo
trình
từ
và
trường
đạo
trình
từ
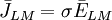 trong
hướng
tiếp
tuyến
với
trục
đối
xứng
trong
hướng
tiếp
tuyến
với
trục
đối
xứng
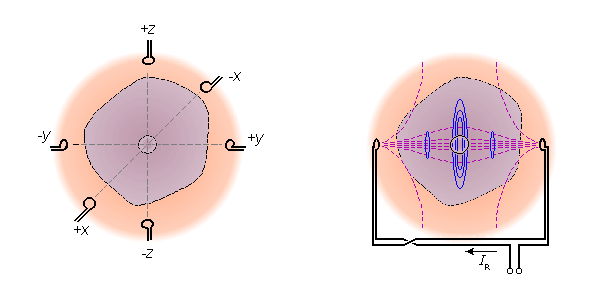
3. Ba trường đạo trình riêng biệt trực giao lẫn nhau từ ba thành phần vuông góc của hệ thống đạo trình hoàn toàn được dò tìm moment lưỡng cực từ của nguồn dòng.
Hình
12.4
trình
bày
nguyên
tắc
cơ
bản
của
hệ
thống
dò
tìm
moment
lưỡng
cực
từ
của
nguồn
khối.
Nó
bao
gồm
một
hệ
thống
cuộn
dây
lưỡng
cực
(hình
12.4A)
cái
mà
tạo
ra
trong
trung
tâm
của
nó
ba
thành
phần
của
từ
trường
biến
thiên
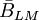 (hình
12.4B).
Chú
ý
rằng
phạm
vi
nơi
mà
cuộn
dây
của
hình
12.4A
tạo
ra
từ
trường
biến
thiên
là
nhỏ
hơn
vì
thế
sẽ
được
giải
thích
sau,
và
do
đó
hình
12.4A
và
12.4B
không
theo
tỉ
lệ.
Ba
thành
phần
từ
trường
(hình
12.4B).
Chú
ý
rằng
phạm
vi
nơi
mà
cuộn
dây
của
hình
12.4A
tạo
ra
từ
trường
biến
thiên
là
nhỏ
hơn
vì
thế
sẽ
được
giải
thích
sau,
và
do
đó
hình
12.4A
và
12.4B
không
theo
tỉ
lệ.
Ba
thành
phần
từ
trường
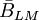 tạo
ra
ba
thành
phần
điện
trường
biến
thiên
tạo
ra
ba
thành
phần
điện
trường
biến
thiên
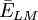 và
trường
đạo
trình
và
trường
đạo
trình
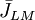 ,
được
minh
họa
trong
hình
12.5.
Điều
quan
trọng
cần
lưu
ý
rằng
từ
trường
biến
thiên
có
dạng
hình
học
giống
điện
trường
biến
thiên
của
đầu
dò
mà
dò
tìm
moment
lưỡng
cực
điện
của
nguồn
khối.
hình
12.24.
,
được
minh
họa
trong
hình
12.5.
Điều
quan
trọng
cần
lưu
ý
rằng
từ
trường
biến
thiên
có
dạng
hình
học
giống
điện
trường
biến
thiên
của
đầu
dò
mà
dò
tìm
moment
lưỡng
cực
điện
của
nguồn
khối.
hình
12.24.
Tương tự như biểu thức của điện trường của nguồn khối, biểu thức 7.9, số hạng thứ hai ở vế phải của biểu thức 12.22 biểu diễn sự đóng góp của đường bao và sự không đồng nhất với moment lưỡng cực từ. Đây là sự tương đương với hiệu ứng của đường bao và sự không đồng nhất trong dạng của trường đạo trình. Nói chung, một đầu sò tạo ra một trường đạo trình lý tưởng trong phạm vi nguồn thay thế cho đường bao và sự không đồng nhất của bộ dẫn khối phát hiện ra moment lưỡng cực của nguồn không bị biến dạng.
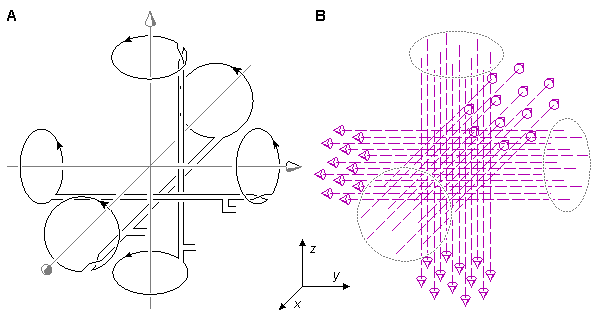
Hình:12.5
Ba
thành
phần
của
trường
đạo
trình
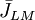 của
một
hệ
thống
lý
tưởng
dò
tìm
moment
lưỡng
cực
từ
của
nguồn
khối.
của
một
hệ
thống
lý
tưởng
dò
tìm
moment
lưỡng
cực
từ
của
nguồn
khối.
Ý
nghĩa
sinh
lý
học
của
lưỡng
cực
từ
Sự phân chia độ nhay ( ví dụ.,trường đạo trình), được minh họa trong hình 12.5, là ý nghĩa sinh lý của phép đo của lưỡng cực từ (tương đương) của một nguồn khối
Tương tự như trong sự dò tìm moment lưỡng cực từ của nguồn khối, định nghĩa của “ý nghĩa sinh lý học” có thể được giải thích trong sự dò tìm của moment lưỡng cực từ của nguồn khối như sau: Khi xem xét các vấn đề phía trước, trường đạo trình minh họa những gì là thành phần (hiệu ứng ) của mỗi tế bào hoạt động với tín hiệu của hệ thống đạo trình. Khi đang xem xét một vấn đề nghịch đảo, trường đạo trình minh họa tương tự hầu hết sự phân bố có thể xảy ra và hướng của tế bào hoạt động khi một tín hiệu được tìm thấy trong một đạo trình
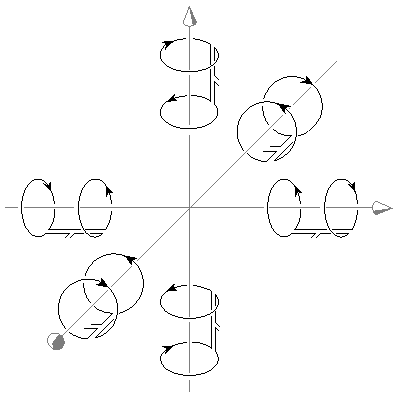
12.6 Quá trình đồng bộ trường đạo trình lý tưởng trong sự dò tìm moment lưỡng cực từ của nguồn khối
Điều kiện đầu:
Nguồn: nguồn khối (tại gốc)
Bộ dẫn khối: hữu hạn, đồng nhất với hệ tọa độ cầu đối xứng
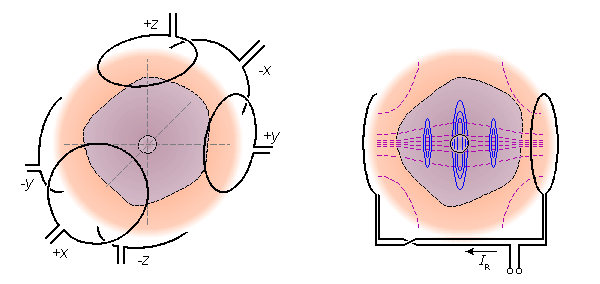
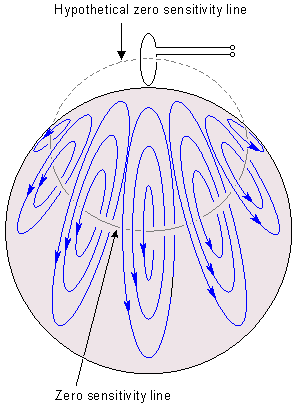
Như trong trường hợp của việc dò tìm moment lưỡng cực điện của nguồn khối, phần 11.6.9, cả đạo trình lưỡng cực và đạo trình đơn cực có thể được sử dụng trong sự đồng bộ trường đạo trình lý tưởng cho việc dò tìm moment lưỡng cực từ của một nguồn khối. Trong trường hợp của một môi trường dẫn khối hữu hạn và điện trường biến thiên đồng nhất, dòng trường đạo trình chảy hướng tâm về trục đối xứng, như được chỉ ra trong hình 12.3. Sau đó không có kết quả thay đổi nếu môi trường dẫn được kết thúc bởi đường bao hình cầu (vì đường chảy đạo trình nằm trong mặt phẳng tiếp tuyến). Mặt cầu bảo đảm dòng đạo trình hiện tại chảy, như hoạt động trong một môi trường đồng nhất hữu hạn, khi từ trường biến thiên đồng nhất được thiết lập theo bất kì hướng tạo độ x-, y-, và z- nào.
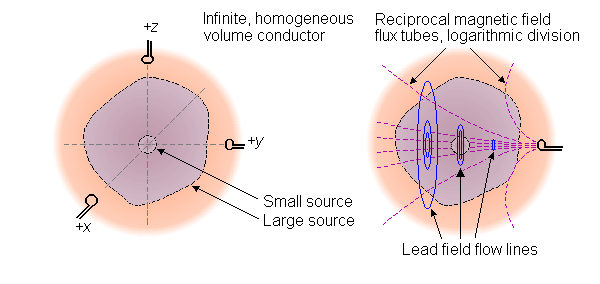
Nếu kích thước của nguồn khối là nhỏ trong trong quan hệ với khoảng cách điểm quan sát, chúng ta có thể xem xét moment lưỡng cực từ như là sự đóng góp từ một nguồn điểm. Vì thế chúng ta xem xét moment lưỡng cực từ như là một vector riêng. Việc đánh giá như vậy một từ trường lưỡng cực có thể hoàn thành thông qua phép đo đơn cực trên mỗi trục tọa độ như được minh họa trong vế trái của hình 12.6. Nếu kích thước của nguồn khối là lớn, chất lượng của hệ thống đạo trình như đã được nói ở trên là không cao. Bởi vì từ trường biến thiên giảm theo hàm khoảng cách, độ nhạy của từ kế đơn là cao hơn cho nguyên tố gần nguồn hơn so với các nguyên tố xa nguồn hơn. Điều này được minh họa ở vế phải của hình 12.6A. Trong hình 12.6 những đường nét đứt thể hiện ống thông lượng từ trường biến thiên. Các dòng tròn cứng mỏng đạidiện cho đường chảy trường đạo trình. Hoạt động của trường đạo trình biến thiên của cuộn từ kế đơn được minh họa một cách chính xác hơn trong hình 20.14, 20.15, 22.3.
Kết
quả
được
nâng
cao
rất
nhiều
nếu
chúng
ra
sử
dụng
cặp
đối
xứng
từ
kế
tạo
ra
đạo
trình
lưỡng
cực,
như
hình
12.6B.
Sự
sắp
xếp
đó
sẽ
tạo
ra
một
trường
đạo
trình
biến
thiên
đồng
nhất
hơn
vùng
nguồn
so
với
được
tạo
ra
với
cuộn
đơn
của
hệ
thống
đạo
trình
lưỡng
cực
(Malmivuo,
1976).
Giống như đối với trường hợp điện, chất lượng của trường đạo trình từ lưỡng cực trong việc đo nguồn khối với kích thước lớn được nâng lên xa hơn bởi sử dụng cuộn dây lớn hơn, kích thước của nó có thể được so sánh với kích thước của nguồn. Điều này được chứng minh trong hình 12.6C.
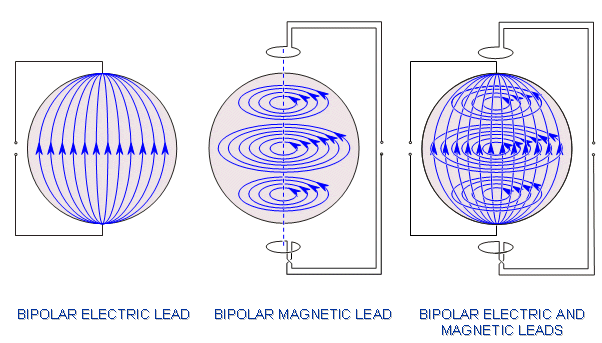
(A) Nếu kích thước nguồn khối là nhỏ so với khoảng cách phép đo thì phương pháp đơn giản nhất là để tạo ra phép đo với đạo trình điểm trên trục tọa độ.
(B) Nếu nguồn khối với kích thước lớn chất lượng của trường đạo trình được cải thiện một cách đáng kể bởi việc sử dụng cặp đối xứng của từ kế tạo ra đạo trình lưỡng cực.
(C) Tăng kích thước của từ kế làm tăng chất lượng đạo trình.
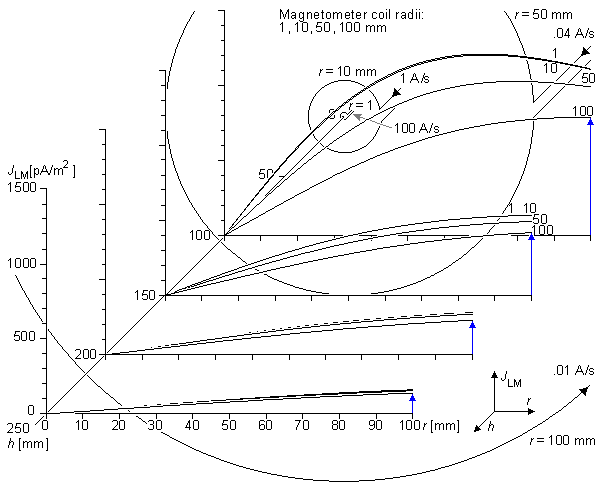
Để mô tả hoạt động của trường đạo trình biến thiên và sự phân bố độ nhạy của đạo trình lưỡng cực như một chức năng của sự tách rời cuộn dây chúgn ta minh họa trong hình 12.7 này cho hai cặp cuộn dây với sự phân bố khác nhau. (chú ý rằng, đường đẳng nhạy không giống với đường từ trường biến thiên). Hình 12.7A minh họa từ trường biến thiên như ống thông lượng xoay tròn cho cuộn Helmholtz, đó là một cặp đồng trục của cuộn tròn riên biệt được tách rời bởi bán kính cuộn. Với sự tách rời cuộn này thành phần bán kính của từ trường kết hợp tại mặt phẳng trung tâm ở mức tối thiểu của nó và và từ trường là rất đồng nhất. Cuộn Helmholtz không thể được sử dụng một cách dễ dàng trong việc dò tìm trường từ sinh học, nhưng chúng có thể được sử dụng trong phép đo độ nhiễm từ hoặc phép đo trở kháng. Chúng được sử dụng rất tốt trong việc cân bằng dụng cụ đo trọng sai và cho sự bù trừ từ trường tĩnh của trái đất trong phép đo môi trường. Hình 12.7B minh họa ống thông lượng từ trường biến thiên cho một cặp cuộn dây với sự phân chia 5r. Hình 12.7C và 12.7D minh họa đường đẳng nhạy cho cuộn dây giống nhau.
Cuối cùng trong chương 20, hình 20.16 minh họa đường đẳng nhạy cho một cặp cuộn dây với sự phân chia 32r. So sánh hai đạo trình lưỡng cực đó với cuộn Helmholtz có thể chú ý rằng trong chúng vùng nhạy đồng nhất là nhỏ hơn so với trong cuộn Helmholtz. Dựa vào trục đối xứng, tính đồng nhât của đạo trình lưỡng cực là tốt hơn so với đạo trình đơn cực tương ứng.
Sự
sắp
xếp
của
đạo
trình
lưỡng
cực
phải
không
được
lẫn
với
hệ
thống
đo
sai
số
hoặc
từ
kế
khác,
mà
nó
bao
gồm
hai
cuộn
dây
đồng
trục
trên
cùng
một
phía
của
nguồn
trong
hướng
đối
diện.
Mục
đích
của
sự
sắp
xếp
này
là
để
loại
bỏ
nhiễu
môi
trường,
không
làm
tăng
chất
lượng
của
trường
đạo
trình.
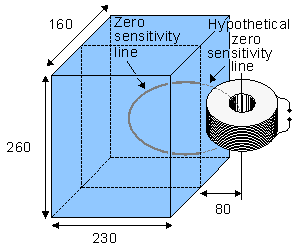
Việc
tìm
ra
hệ
thống
đạo
trình
lượng
cực
với
dụng
cụ
đo
trọng
sai
được
minh
họa
trong
hình
12.8.
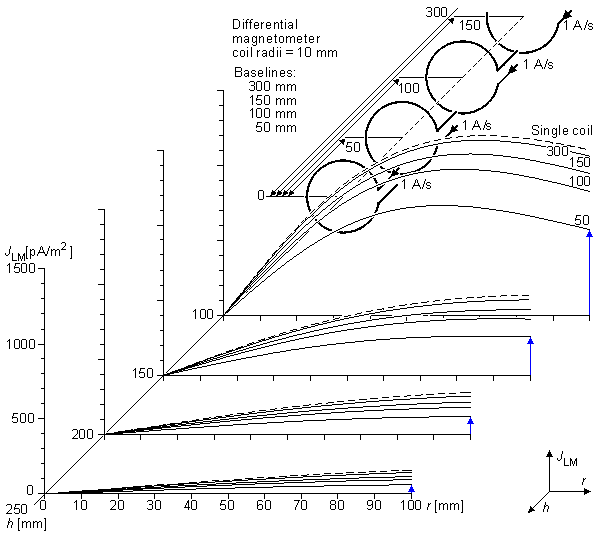
Hình
cuối
cùng
12.20
minh
họa
hiệu
ứng
của
cuộn
dây
thứ
hai
trong
sự
phân
chia
độ
nhạy
dụng
cụ
đo
trọng
sai
với
vài
đường
cơ
bản.
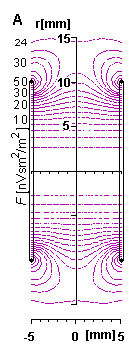
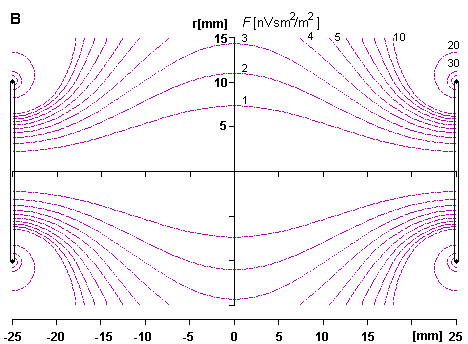
Hình 12.7:Ống thông lượng của từ trường biến thiên của
(A)
cuộn
dây
Helmholtz
có
một
sự
tách
rời
cuộn
r
(B)
đạo
trình
lưỡng
cực
với
sự
tách
rời
cuôn
5r
đường
đẳng
nhạy
cho
(C)
cuộn
dây
Helmholtz
có
một
sự
tách
rời
cuộn
r
(D)
đạo
trình
lưỡng
cực
với
sự
tách
rời
cuộn
5r
(chú
ý
rằng
đường
đẳng
nhạy
khác
với
ống
thông
lượng
của
từ
trường
biến
thiên).
.
12.7 Sự so sánh trường đạo trình của đạo trình lưỡng cực lý tưởng với việc dò tìm moment lưỡng cực từ và điện của nguồn khối
Điều kiện đâu:
Nguồn: moment lưỡng cực điện và từ của nguồn khối
Bộ dẫn khối: hữu hạn, đồng nhất
Trong phần tóm tắt, chúng ta chú ý chi tiết sau từ trường đạo trình của hệ thống đạo trình lưỡng cực lý tưởng cho việc dò tìm moment lưỡng cực điện và từ của nguồn khối.
12.7.1 Hệ thống đạo trình lưỡng cực cho việc dò tìm moment lưỡng cực điện
1.Hệ thống đạo trình bao gồm ba thành phần
2. Với một bộ dẫn khối đối xứng cầu, mỗi bộ được tạo ra bởi một cặp điện cực, trục của nó nằm trên hướng của hệ trục tọa độ. Mỗi điện cực nằm trên phía đối diện với nguồn, được chỉ ra trong hình 11.24.
3. Mỗi thành phần, khi dòng được đưa vào một cách biến thiên, một điện trường đồng nhất và tuyến tính được thiết lập trong phạm vi của nguồn khối (xem hình 11.25).
4.Mỗi
điện
trường
biến
thiên
tạo
ra
một
trường
dòng
tương
tự,
mà
nó
được
gọi
là
trường
đạo
trình
điện
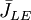 .
(chú
ý
sự
tương
đồng
trong
hình
11.25,
minh
họa
điện
trường
biến
thiên
.
(chú
ý
sự
tương
đồng
trong
hình
11.25,
minh
họa
điện
trường
biến
thiên
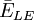 của
điện
trường,
và
hình
12.7,
minh
họa
từ
trường
biến
thiên
của
điện
trường,
và
hình
12.7,
minh
họa
từ
trường
biến
thiên
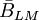 của
từ
trường.)
của
từ
trường.)
12.7.2 Hệ thống đạo trình lưỡng cực cho việc dò tìm moment lưỡng cực từ
1.Hệ thống bao gồm ba thành phần
2. Trong trường hợp đối xứng cầu, mỗi thành phần được tạo ra bởi một cặp từ kế (hoặc dụng cụ đo trọng sai) được đặt trong hướng của trục tọa độ đối diện với nguồn, được minh họa trong hình 12.6C (hoặc 12.8).
3. Với mỗi thành phần, khi dòng được đưa vào một cách biến thiên, từ trường đồng nhất và tuyến tính được thiết lập trong phạm vi của nguồn khối, được chỉ ra trong hình 12.4
4.
Mỗi
từ
trường
biến
thiên
tạo
ra
một
điện
trường,
nhất
thiết
tiếp
tuyến
với
đường
bao.
Những
điện
trường
biến
thiên
này
sinh
ra
một
điện
trường
dòng
giống
nhau,
nó
được
gọi
là
trường
đạo
trình
từ
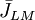 ,
được
mô
tả
trong
hình
12.5
,
được
mô
tả
trong
hình
12.5
Những hình 12.8, 12.4, và 12.5 ở trên cho phép chúng ta dễ dàng hơn để có thể nhìn thấy sự tạo ra và hình dạng của trường đạo trình của từ trường.
12.8 Độ nhạy tiếp tuyến và bán kính của hệ thống đạo trình dò tìm moment lưỡng cực điện và từ của một nguồn khối
Điều kiện đầu:
Nguồn: moment lưỡng cực điện và từ của nguồn khối
Bộ dẫn khối: hữu hạn đồng nhất
12.8.1 Độ nhạy của đạo trình điện
Độ nhạy tiếp tuyến và bán kính của hệ thống đạo trình dò tìm moment lưỡng cực điện của một nguồn khối có thể được ước lượng dễ dàng cho trường hợp nơi mà một trường đạo trình lý tưởng đã từng được thiết lập.
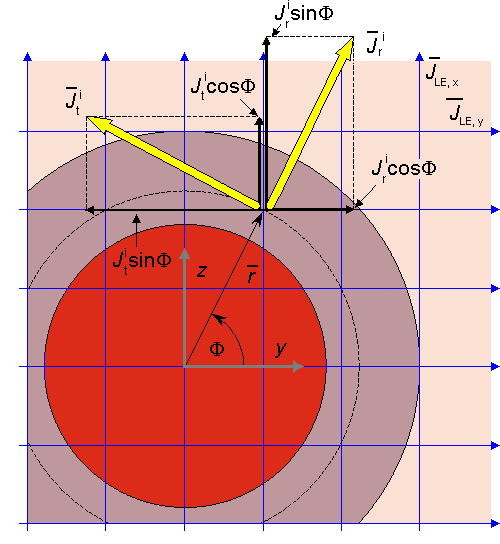
Hình
12.9
mô
tả
phần
mặt
cắt
của
một
nguồn
khối
hình
cầu
trong
một
nguồn
khối
đồng
nhất
đẳng
hướng
và
hai
thành
phần
của
trường
đạo
trình
cho
việc
dò
tìm
moment
lưỡng
cực
điện.
Đặt
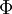 là
góc
giữa
đường
chảy
trường
đạo
trình
điện
theo
trục
hoành
và
vector
bán
kính
là
góc
giữa
đường
chảy
trường
đạo
trình
điện
theo
trục
hoành
và
vector
bán
kính
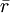 từ
tâm
của
nguồn
hình
cầu
tới
điểm
tại
vị
trí
mà
yếu
tố
nguồn
tiếp
tuyến
và
bán
kính
từ
tâm
của
nguồn
hình
cầu
tới
điểm
tại
vị
trí
mà
yếu
tố
nguồn
tiếp
tuyến
và
bán
kính
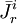 và
và
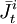 ,
tương
ứng,
đặt
tại
đó.
Dựa
vào
biểu
thức
11.30,
điện
thế
đạo
trình
,
tương
ứng,
đặt
tại
đó.
Dựa
vào
biểu
thức
11.30,
điện
thế
đạo
trình
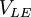 tỉ
lệ
thuận
với
hình
chiếu
của
mật
độ
dòng
được
đưa
vào
tỉ
lệ
thuận
với
hình
chiếu
của
mật
độ
dòng
được
đưa
vào
 trên
dòng
chảy
đường
đạo
trình.
Độ
nhạy
của
trường
đạo
trình
tổng
là
tổng
độ
nhạy
của
hai
đạo
trình
thành
phần;
vì
thế
với
thành
phần
bán
kính
trên
dòng
chảy
đường
đạo
trình.
Độ
nhạy
của
trường
đạo
trình
tổng
là
tổng
độ
nhạy
của
hai
đạo
trình
thành
phần;
vì
thế
với
thành
phần
bán
kính
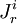 ta
có:
ta
có:
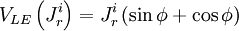 (12.26)
(12.26)Trong khi với thành phần tiếp tuyến ta có
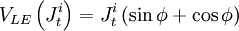 (12.27)
(12.27)Trong những biểu thức trên trường đạo trình thanh phần được giả sử là đồng nhất và độ lớn đơn vị
Chúng
ta
chú
ý
từ
biểu
thức
12.26
và
12.27
độ
nhạy
tổng
của
hai
thành
phần
của
đạo
trình
điện
với
thành
phần
nguồn
dòng
bán
kính
và
tiếp
tuyến
 i
là
bằng
nhau
và
không
phụ
thuộc
vào
vị
trí
của
chúng.
i
là
bằng
nhau
và
không
phụ
thuộc
vào
vị
trí
của
chúng.
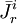 và
và
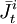
12.8.2 Độ nhạy của đạo trình từ
Từ biểu thức 12.13 và từ định nghĩa moment từ lưỡng cực của nguồn khối (xem biểu thức 12.22), nó có thể được xem là hệ thống đạo trình từ và thành phần của nó chỉ nhạy với thành phần tiếp tuyến của nguồn. Độ lớn của độ nhạy là, như đã chú ý trước đây, tỉ lệ thuận với khoảng cách từ trục đối xứng.
12.9 Thành phần đặc biệt của trường đạo trình từ
Điều kiện đầu:
Nguồn:
Bộ dẫn khối: hữu hạn. không đồng nhất, đối xứng trụ.
Thành phần đặc biệt của trường đạo trình điện, được liệt kê ở phần 11.6.10, cũng thuộc trường đạo trình từ. Trường đạo trình từ cũng có một số thành phần đặc biệt được tổng kết dưới đây.
1.Nếu bộ dẫn khối bị cắt hoặc đường bao của tính không đồng nhất được chèn vào theo đường chảy dòng trường đạo trình, hình dạng của trường đọa trình không thay đổi (malmivuo, 1976). Điều này giải thích tại sao hoặc là bộ dẫn nguồn khối hình trụ hoặc là hình cầu, thì hình dạng của trường đạo trình từ đối xứng là không bị ảnh hưởng. Có hai hệ quả quan trọng sau:
1.1 Bởi vì tim có thể được xem như có dạng như hình cầu, khối lượng máu trong tim có độ dẫn cao, có thể được coi như là hình cầu và đồng tâm, không thay đổi hình dạng của trường đạo trình. Điều này có nghĩa là hiệu ứng Brody không tồn tại trong từ tâm đồ (xem chương 18).
1.2 Độ dẫn kém của sọ không ảnh hưởng đến việc dò từ của hoạt động não khi nó họat động với việc dò điện (xem hình 12.10).
2. Trường đạo trình từ trong bộ dẫn khối chỉ ra đối xứng cầu luôn luôn có hướng tiếp tuyến. Điều này có nghĩa là độ nhạy của đạo trình từ trong một bộ dẫn khối hình cầu với lưỡng cực điện bán kính là luôn bằng 0. Thực tế này có tầm quan trọng đặc biệt trong MEG (xem hình 12.11).
3. Nếu điện cực của đạo trình điện lưỡng cực đối xứng được đặt trên trục đối xứng của đầu dò từ trường lưỡng cực được sắp xếp cho một bộ dẫn khối, trường đạo trình của đạo trình điện và từ là bình thường với mỗi trường thông qua bộ dẫn khối, như minh họa trong hình 12.12 (Malmivuo, 1980). (cùng giữ cho đạo trình đơn cực là tốt, mặc dù không được chỉ ra trong hình).
4. Trường đạo trình của tất cả đạo trình từ bao gồm ít nhất một đường nhạy 0, nơi mà độ nhạy của lưỡng cực điện băng 0. Đường này tồn tại trong tất cả các bộ dẫn khối, trừ khi có một lỗ trong bộ dẫn khối trong vùng này (Eskola, 1979, 1983; Eslola và Malmivuo, 1983). Tự đường nhạy 0 nó đã là một công cụ trong việc hiểu biết hình dạng của đạo trình từ (như được minh họa trong hình 12.13).
5. Lý thuyết biến thiên cũng được áp dụng cho trường hợp tương hỗ. Điều này có nghĩa rằng trong một mô hình bể chứa nó có thể cung cấp một dòng “tương hỗ một cách biến thiên” cho lưỡng cực trong bộ dẫn khối và để đo tín hiệu từ đạo trình. Tuy nhiên, kết quả có thể không được lý giải như đã từng thu được bằng cách cung cấp dòng biến thiên cho đạo trình với tín hiệu được đo từ lưỡng cực. Lợi ích của sự sắp xếp “tương hỗ biến thiên” là vì lý do kĩ thuật tỉ số nhiễu tín hiệu có thể được cải thiện trong khi chúng ta vẫn có lợi ích của việc lý giải kết quả như sự phân chia của dòng trường đạo trình trong bộ dẫn khối (Malmivuo, 1976).
12.10 Sự độc lập của trường điện sinh học và từ sinh học và phép đo
12.10.1 Sự độc lập của nguồn dòng và nguồn xoáy
Thuyết của Helmholtz (Morse and Feshbach, 1953; Plonsey and Collin, 1961) nói:
“trường vector chung , không xuất hiện ở vô cực, có thể được biểu diễn hoàn toàn như tổng của hai trường vector riêng biệt; một là không xoáy (curl 0) và một là thuộc solenoit (không phân kì).”
Mật độ dòng được đưa vào là trường vector không xuất hiện ở vô cực và, dựa và lý thuyết, có thể được tính như tổng của hai thành phần:
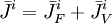 (12.28)
(12.28)
ở
đây
F
và
V
viết
tắt
cho
dòng
và
xoáy,
tương
ứng.
Từ
định
nghĩa,
những
trường
vector
này
thỏa
mãn
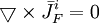 và
và
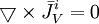 .
.
Đầu tiên chúng ta ví dụ về tính độc lập của tín hiệu điện và trường trong trường hợp đồng nhất hữu hạn, khi số hạng thứ hai ở vế phải của biểu thức 7.10 và 12.6, được gây ra bởi tính đồng nhất, là bằng 0. Biểu thức này có thể được viêt lại cho điện thế:
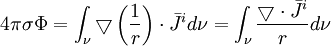 (12.19)
(12.19)Và cho từ trường:
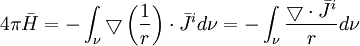 (12.20)
(12.20)
Thế
biểu
thức
12.18
vào
biểu
thức
12.19
và
12.30
chỉ
ra
rằng
dưới
điều
kiện
đồng
nhất
là
không
cận,
trường
điện
sinh
học
sinh
ra
từ
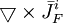 ,
đó
là
nguồn
dòng
(biểu
thức
7.5),
và
trường
từ
sinh
học
sinh
ra
từ
,
đó
là
nguồn
dòng
(biểu
thức
7.5),
và
trường
từ
sinh
học
sinh
ra
từ
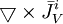 ,
đó
là
nguồn
xoáy
(biểu
thức
12.17).
Kể
từ
khi
phát
hiện
trường
từ
sinh
học
đầu
tiên,
từ
tâm
đồ,
bởi
Baule
và
McFee
in
1963
(Baule
and
McFee,
1963),
những
chứng
minh
được
bàn
ở
trên
đưa
ra
rất
nhiều
sự
lạc
quan
giữa
các
nhà
khoa
học.
Nếu
sự
độc
lập
này
được
khẳng
định,
sự
dò
tìm
từ
tính
của
hoạt
động
điện
sinh
học
có
thể
mang
đến
nhiểu
thông
tin
mới
mà
không
thấy
ở
phép
đo
điện.
,
đó
là
nguồn
xoáy
(biểu
thức
12.17).
Kể
từ
khi
phát
hiện
trường
từ
sinh
học
đầu
tiên,
từ
tâm
đồ,
bởi
Baule
và
McFee
in
1963
(Baule
and
McFee,
1963),
những
chứng
minh
được
bàn
ở
trên
đưa
ra
rất
nhiều
sự
lạc
quan
giữa
các
nhà
khoa
học.
Nếu
sự
độc
lập
này
được
khẳng
định,
sự
dò
tìm
từ
tính
của
hoạt
động
điện
sinh
học
có
thể
mang
đến
nhiểu
thông
tin
mới
mà
không
thấy
ở
phép
đo
điện.
Rush là người đầu tiên nhận thấy rằng sự độc lập của tín hiệu điện và từ chỉ là một khả năng toán học và vật lý hạn chế xảy ra mà nó yêu cầu nguồn dòng và nguồn xoáy, và hậu quả là trường điện và từ, về cơ bản là phụ thuộc lẫn nhau trong bộ dẫn khối đồng nhất (Rush, 1975). Điều này có thể được minh họa một cách dễ dàng với một ví dụ được ghi nhận, ví dụ, khi tâm nhĩ của tim co, hoạt động điện sinh học của nó tạo ra một điện trường được ghi lại như là sóng P trong ECG. Cùng thời gian đó họat động điện của nó tạo ra một từ trường được tìm thấy như sóng P của MCG. Tương tự QRS-complexes điện và từ và sóng T được tương quan với nhau, một cách tương ứng. Vì thế, sự độc lập hoàn toàn giữa ECG và MCG là không thể.
Trong một số thông tin mới đây, Plonsey (1982) đã chỉ ra rằng nguồn tế bào chính có thể nhỏ so với nguồn tế bào thứ cấp và điều cuối cùng có thể được đặc trưng như một nguồn hai lớp cho cả thành phần vector từ và điện vô hướng.
12.10.2 Sự giải thích lý thuyết trường đạo trình của sự độc lập của phép đo trường
Vấn đề về sự độc lập của điện trường và từ trường của nguồn khối và sự giải thích về lý thuyết của Helmholtz có thể được giải thích tốt hơn việc sử dụng lý thuyết trường đạo trình. Chúng ta bạn luận vấn đề này trong sự liên kết với lưỡng cực điện và từ tương đương của nguồn khối. Tất nhiên, sự thảo luận này có thể được dễ dàng mở rộng tốt với nhiều nguồn phức tạp hơn.
Như
được
giải
thích
trong
phần
11.6.6
trường
đạo
trình
điện
được
đưa
ra
bởi
biểu
thức
11.54.
Như
được
trình
bày
trong
phần
11.6.7,
hệ
thống
đạo
trình
dò
tìm
moment
lưỡng
cực
điện
của
một
nguồn
khối
bao
gồm
ba
điện
trường
biến
thiên
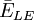 trực
giao,
tuyến
tính
và
đồng
nhất,
sinh
ra
ba
trường
đạo
trình
điện
trực
giao,
tuyến
tính
và
đồng
nhất,
sinh
ra
ba
trường
đạo
trình
điện
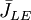 trực
giao,
tuyến
tính
và
đồng
nhất.
Ba
đạo
trình
này
là
độc
lập
với
nhau
và
chúng
dò
tìm
ba
thành
phần
trực
giao
của
nguồn
dòng.
trực
giao,
tuyến
tính
và
đồng
nhất.
Ba
đạo
trình
này
là
độc
lập
với
nhau
và
chúng
dò
tìm
ba
thành
phần
trực
giao
của
nguồn
dòng.
Như
được
thảo
luận
trong
phần
12.3
trường
đạo
trình
từ
được
đưa
ra
bởi
công
thức
12.11.
nó
đã
chỉ
ra
trong
phần
12.5
rằng
hệ
thống
đạo
trình
dò
tìm
moment
lưỡng
cực
từ
của
một
nguồn
khối
bao
gồm
ba
từ
trường
biến
thiên
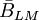 trực
giao,
tuyến
tính
và
đồng
nhất,
nó
sinh
ra
ba
trường
đạo
trình
từ
trực
giao,
tuyến
tính
và
đồng
nhất,
nó
sinh
ra
ba
trường
đạo
trình
từ
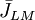 LM
trực
giao,
tuyến
tính
va
đồng
nhất.
Ba
đạo
trình
đó
cũng
độc
lập
với
nhau
và
chúng
dò
tìm
ba
thành
phần
trực
giao
của
nguồn
xoáy.
LM
trực
giao,
tuyến
tính
va
đồng
nhất.
Ba
đạo
trình
đó
cũng
độc
lập
với
nhau
và
chúng
dò
tìm
ba
thành
phần
trực
giao
của
nguồn
xoáy.
Trong ví dụ đã được đề cập trước đây, nhờ vào thuyết Helmholtz, ba trường đạo trình điện độc lập là độc lập với ba trường đạo trình từ độc lập. Nói cách khác, không đạo trình nào trong sáu đạo trình trên là sự kết hợp tuyến tính của năm đạo trình còn lại. Tuy nhiên, trong trường hợp nguồn khối sinh lý, điện trường và từ trường và ba thành phần trực giao của chúng mà sáu đạo trình đó dò ra là không độc lập hoàn toàn, bởi vì khi nguồn họat động, nó sinh ra tất cả ba phép cộng ba thành phần của điện trường và từ trường trong cách mà kết nối chúng với nhau. Vì thế, trong khi tất cả sau đạo trình này của hệ thống đạo trình vector điện từ có khả năng phát hiện sự độc lập của một nguồn, khả năng đó không cần thiết được nhận ra.
Nó sẽ được chỉ ra trong chương 20 với sự thảo luận về từ tâm đồ mà khi đo moment lưỡng cực điện và từ của một nguồn, cả những phương pháp bao gồm ba đạo trình độc lập và bao gồm khối lượng thông tin giống nhau từ nguồn. Tuy nhiên, thông tin của những phép đo này là khác nhau và vì thế những nhóm bệnh nhân khác nhau được chẩn đoán phù hợp với phương pháp không giống nhau. Nếu trong chẩn đoán tín hiệu điện và từ được sử dụng một cách đồng thời, nhóm bệnh nhân được chẩn doán phù hợp có thể được kết hợp và tất cả quá trình chẩn đoán sẽ giảm bớt. Điều này cũng có thể được giải thích bởi chú ý rằng trong phương pháp kết hợp chúng ta có tổng đại sô 3 + 3 =6 đạo trình độc lập. Điều này giảm tổng khối lượng thông tin thu được từ nguồn.
12.11 Sự phân bố của đạo trình từ cơ bản
Điều kiện đầu:
Nguồn: nguồn khối
Bộ dẫn khối: hữu hạn, không đồng nhất, đối xứng trụ
12.11.1 Biêu thức của phép tính sự phân bố độ nhạy của đạo trình từ cơ bản
Bởi vì trong bộ dẫn khối hữu hạn đồng nhất đường chảy trường đạo trình từ xoay tròn quanh trục đối xứng, rất dễ để tính dự phân bố độ nhạy của một đạo trình từ trong một bộ dẫn khối đối xứng trụ, mà trục đối xứng của nó trùng với trục của từ kế. Sau đó kết quả có thể được trình bày như một hàm của khoảng cách từ trục đối xứng với khoảng cách từ đầu dò như một tham số (Malmivuo, 1976).
Hình
12.14
minh
họa
cuộn
dây
từ
kế
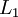 và
một
đường
chảy
dòng
trường
đạo
trình
được
đặt
đồng
trục
và
một
đường
chảy
dòng
trường
đạo
trình
được
đặt
đồng
trục
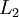 .
Từ
thông
.
Từ
thông
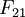 kết
nối
vòng
lặp
kết
nối
vòng
lặp
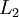 nhờ
vào
dòng
được
đưa
vào
biến
thiên
nhờ
vào
dòng
được
đưa
vào
biến
thiên
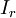 trong
cuộn
dây
từ
kế
được
tính
toán
một
cách
dễ
dàng
nhất
sử
dụng
thế
vector
từ
trong
cuộn
dây
từ
kế
được
tính
toán
một
cách
dễ
dàng
nhất
sử
dụng
thế
vector
từ
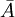 tại
vòng
lặp
tại
vòng
lặp
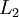 (Smythe,
1968,
p.
290).
(Smythe,
1968,
p.
290).
Định luật Faraday phát biểu rằng một từ trường thay đổi theo thời gian bao gồm lực điện động mà tích phân đường của nó xung quanh một vòn khép kín bằng độ thay đổi của từ thông qua vòng mạch điện kín.
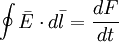 (12.31)
(12.31)
ở
đây
F
=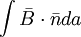 da
là
từ
thông
được
đánh
giá
bằng
tích
phân
của
thành
phần
bình
thường
của
cảm
ứng
từ
da
là
từ
thông
được
đánh
giá
bằng
tích
phân
của
thành
phần
bình
thường
của
cảm
ứng
từ
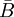 cắt
qua
mặt
phẳng
của
vòng.
Với
một
vòng
tròn
tích
phân
ở
vế
trái
của
biểu
thức
12.31
bằng
cắt
qua
mặt
phẳng
của
vòng.
Với
một
vòng
tròn
tích
phân
ở
vế
trái
của
biểu
thức
12.31
bằng
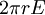 ,
ở
đây
r
là
bán
kính
của
vòng,
và
chúng
ta
thu
được
mật
độ
dòng
,
ở
đây
r
là
bán
kính
của
vòng,
và
chúng
ta
thu
được
mật
độ
dòng
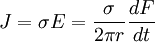 (12.32)
(12.32)
ở
đây
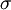 là
độ
dẫn
của
môi
trường.
Mật
độ
dòng
có
hướng
tiếp
tuyến.
Bây
giờ
vấn
đề
được
giảm
bớt
cho
việc
xác
định
từ
thông
kết
nối
mộ
vòn
tròn
trong
môi
trường
nhờ
vào
một
dòng
điện
được
đưa
vào
một
cách
biến
thiên
trong
cuộn
từ
kế
được
đặt
đồng
trục.
là
độ
dẫn
của
môi
trường.
Mật
độ
dòng
có
hướng
tiếp
tuyến.
Bây
giờ
vấn
đề
được
giảm
bớt
cho
việc
xác
định
từ
thông
kết
nối
mộ
vòn
tròn
trong
môi
trường
nhờ
vào
một
dòng
điện
được
đưa
vào
một
cách
biến
thiên
trong
cuộn
từ
kế
được
đặt
đồng
trục.
Phương trình cơ bản cho phép tính thế vector tại điểm P dựa vào một dòng I sau trong một bộ dẫn khối mỏng là
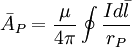 (12.33)
(12.33)
ở
dây
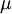 là
độ
từ
thẩm
của
môi
trường;
là
độ
từ
thẩm
của
môi
trường;
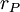 là
khoảng
cách
từ
yếu
tố
bộ
dẫn
khối
đến
điểm
P
là
khoảng
cách
từ
yếu
tố
bộ
dẫn
khối
đến
điểm
P
Biểu
thức
này
có
thể
được
sử
dụng
để
tính
thế
từ
vector
tại
điểm
P
trong
hình
12.14.
Từ
trục
đối
xứng
chúng
ta
biết
rằng
trong
tọa
độ
cầu
độ
lớn
của
là
độc
lập
với
góc
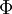 .
Vì
thế,
để
đơn
giản,
chúng
ta
chọn
điểm
P
sao
cho
.
Vì
thế,
để
đơn
giản,
chúng
ta
chọn
điểm
P
sao
cho
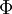 =
0.
chú
ý
rằng
những
yếu
tố
ở
khoảng
cách
bằng
nhau
của
độ
dài
=
0.
chú
ý
rằng
những
yếu
tố
ở
khoảng
cách
bằng
nhau
của
độ
dài
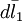 tại
+
tại
+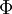 và
–
và
–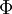 được
ghép
thành
cặp,
kết
quả
là
bình
thường
cho
hr.
Vì
thế
được
ghép
thành
cặp,
kết
quả
là
bình
thường
cho
hr.
Vì
thế
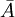 chỉ
có
một
thành
phần
chỉ
có
một
thành
phần
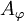 .
Nếu
biểu
diễn
.
Nếu
biểu
diễn
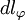 theo
thành
phần
theo
thành
phần
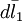 ,
sau
đó
biểu
thức
12.33
có
thể
được
viết
lại
như
sau:
,
sau
đó
biểu
thức
12.33
có
thể
được
viết
lại
như
sau:
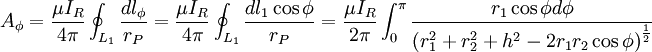 (12.34)
(12.34)
Từ
thông
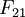 F21
có
thể
được
tính
từ
thế
vector:
F21
có
thể
được
tính
từ
thế
vector:
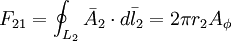 (12.35)
(12.35)
Nếu
thế
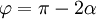 ,
nó
trở
thành
,
nó
trở
thành
![F_{{21}}=\mu I_{R}{\sqrt {r_{1}r_{2}}}\int _{{0}}^{{{\frac {\pi }{2}}}}{\frac {k\left(2\sin ^{2}\alpha -1\right)}{{\sqrt {1-k^{2}\sin ^{2}\alpha }}}}d\alpha =\mu I_{R}{\sqrt {h^{2}+{\left(r_{1}+r_{2}\right)}^{2}}}\left[\left(1-{\frac {k^{2}}{2}}\right)K\left(k\right)-E\left(k\right)\right]](https://tusach.thuvienkhoahoc.com/images/math/5/5/7/557492abe0a5ebdb34c0208207549d89.png) (12.36)
(12.36)ở đây
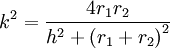 (12.37)
(12.37)Và K(k) và E(k) là tích phân ellip đầy đủ của dạng thứ nhất và thứ hai, một cách tương ứng. chúng được tính từ biểu thức 12.38A,B. (Abramowitz and Stegun, 1964, p. 590) and K(k) and E(k) are complete elliptic integrals of the first and second kind, respectively. These are calculated from equations 12.38A,B. (Abramowitz and Stegun, 1964, p. 590)
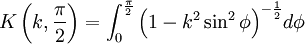 (12.38a)
(12.38a)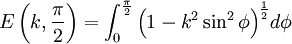 (12.38b)
(12.38b)Giá trị K(k) và E(k) cũng có thể được tính bằng dẫy sau
![K\left(k,{\frac {\pi }{2}}\right)={\frac {\pi }{2}}\left[1+\left[{\frac {1}{2}}\right]^{2}k^{2}+\left[{\frac {3}{2\cdot 4}}\right]^{2}k^{4}+\left[{\frac {3\cdot 5}{2\cdot 4\cdot 6}}\right]^{2}k^{6}+\bullet \bullet \bullet \right]](https://tusach.thuvienkhoahoc.com/images/math/d/a/a/daa8d61268cb42644c122eab72ec07eb.png) (12.39a)
(12.39a)![E\left(k,{\frac {\pi }{2}}\right)={\frac {\pi }{2}}\left[1-\left[{\frac {1}{2}}\right]^{2}k^{2}-\left[{\frac {3}{2\cdot 4}}\right]^{2}{\frac {k^{4}}{3}}-\left[{\frac {3\cdot 5}{2\cdot 4\cdot 6}}\right]^{2}{\frac {k^{6}}{5}}+\bullet \bullet \bullet \right]](https://tusach.thuvienkhoahoc.com/images/math/7/8/2/782f32eeb1b746bfcc0eb566e2409551.png) (12.39b)
(12.39b)Phép tính K(k) and E(k) nhanh hơn từ dãy, nhưng chúng cho những kết quả không chính xác tại khoảng cách nhỏ từ cuộn dây và vì thế việc sử dụng biểu thức 12.38A, B được khuyên dùng.
Thế biểu thức 12.36 vào 12.32 cho mật độ dòng trường đạo trình như một hàm của độ thay đổi của dòng cuộn dây trong từ kế có dòng được đưa và biến thiên
![J_{{LM}}={\frac {\sigma 4\pi \cdot 10^{{-7}}}{2\pi r_{2}}}{\sqrt {h^{2}+\left(r_{1}+r_{2}\right)^{2}}}\left[\left(1-{\frac {k^{2}}{2}}\right)K\left(k\right)-E\left(k\right)\right]{\frac {dI_{R}}{dt}}](https://tusach.thuvienkhoahoc.com/images/math/2/1/b/21b2a337b07b3a225aaa726cde7cdc00.png) (12.40)
(12.40)Bởi vì chúng ta quan tâm đến sự phân bố độ nhạy và không chú ý đến độ nhạy tuyệt đối với tần số trung tâm hoặc giá trị độ dẫn, kết quả của biểu thức 12.40 có thể được chuẩn hóa bằng định nghĩa (tương tự như làm với phần 12.3.1 trong sự chuyển biểu thức cho trường đạo trình từ)
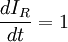
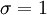 (12.41)
(12.41)Và chúng ta thu được biểu thức từ việc tính toán mật độ dòng trường đạo trình cho một từ kế cuộn dây đơn trong bộ dẫn khối đồng nhất hữu hạn:
![J_{{LM}}={\frac {2\pi \cdot 10^{{-7}}}{r_{2}}}{\sqrt {h^{2}+\left(r_{1}+r_{2}\right)^{2}}}\left[\left(1-{\frac {k^{2}}{2}}\right)K\left(k\right)-E\left(k\right)\right]](https://tusach.thuvienkhoahoc.com/images/math/c/0/0/c00ab4339319a7135db02e68f140abb8.png) (12.42)
(12.42)
ở
đây
tất
cả
khoảng
cách
được
đo
ra
m,
và
mật
độ
dòng
trong
[A/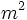 ].
].
Nếu
khoảng
cách
h
là
lớn
so
với
bán
kính
cuộn
dây
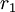 và
bán
kính
đường
chảy
dòng
trường
đạo
trình
và
bán
kính
đường
chảy
dòng
trường
đạo
trình
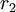 ,
cảm
ứng
từ
bên
trong
đường
sức
có
thể
được
xem
như
là
không
đổi,
và
biểu
thức
12.42
được
đơn
giản
hóa
rất
nhiều.
Giá
trị
của
từ
thông
trở
thành
,
cảm
ứng
từ
bên
trong
đường
sức
có
thể
được
xem
như
là
không
đổi,
và
biểu
thức
12.42
được
đơn
giản
hóa
rất
nhiều.
Giá
trị
của
từ
thông
trở
thành
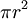 .
Thế
nó
vào
biểu
thức
12.32,
ta
có
.
Thế
nó
vào
biểu
thức
12.32,
ta
có
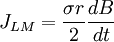 (12.43)
(12.43)Cảm ứng từ có thể được tính trong trường hợp này như cho một nguồn lưỡng cực. Biểu thức 12.43 chỉ ra một cách rõ ràng rằng trong vùng cảm ứng từ không đổi và độ dẫn không đổi, mật độ dòng trường đạo trình tỉ lệ thuận với khoảng cách bán kính từ trục đối xứng. Chú ý rằng biểu thức này phù hợp với biểu thức 12.11.
12.11.2 Mật độ dòng trường đạo trình của một trường đạo trình đơn cực của từ kế một cuộn dây
Do đối xứng, mật độ dòng trường đạo trình là độc lập với góc Φ trong hình 12.14. Vì thế, mật độ dòng trường đạo trình có thể được đặt như một hàm của khoảng cách bán kính r từ trục đối xứng với khoảng cách h từ từ kế như là một tham số. Hình 12.15 chỉ ra sự phân bố mật độ dòng trường đạo trình của đạo trình đơn cực được tạo ra bởi từ kế một cuộn dây với bán kính cuộn dây là 10mm trong một bộ dẫn khối đối xứng trụ được tính từ biểu thức 12.42. Mật độ dòng trường đạo trình có hướng tiếp tuyến. (với thang đo tỉ lệ, hình vẽ có thể được sử dụng cho nghiên cức những khoảng cách phép đo khác nhau)
Hình 12.15 chỉ ra rằng trong một đạo trình đơn cực mật độ dòng trường đạo trình là phụ thuộc mạnh mẽ vào khoảng cách cuộn dây từ kế. Nó cũng chỉ ra rằng kích thước nhỏ của vùng mà mật độ dòng trường đạo trình giảm xấp xỉ tuyến tính như một hàm của khoảng cách bán kính từ trục đối xứng, nhất là gần cuộn dây.
Đường
nét
đứt
trong
hình
12.15
là
những
đường
đẳng
nhạy;
tham
gia
các
điểm
nơi
mà
mật
độ
dòng
trường
đạo
trình
là
100,
200,
300,
400,
và
500pA/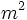 ,
tương
ứng,
như
được
chỉ
ra
bởi
những
số
in
nghiêng.
,
tương
ứng,
như
được
chỉ
ra
bởi
những
số
in
nghiêng.
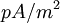 ,
tương
ứng,
như
được
chỉ
ra
bởi
những
số
in
nghiêng.
,
tương
ứng,
như
được
chỉ
ra
bởi
những
số
in
nghiêng.
Hình
12.16
minh
họa
đường
đẳng
nhạy
cho
một
từ
kế
một
cuộn
dây
của
hình
12.15;
bán
kính
cuộn
dây
là
10mm,
và
bộ
dẫn
khối
là
đối
xứng
cầu.
Trục
tung
chỉ
ra
khoảng
cách
h
từ
từ
kế
và
trục
hoành
khoảng
cách
bán
kính
r
từ
trục
đối
xứng.
Trục
đối
xứng,
được
vẽ
với
đường
nét
đứt
đậm,
là
đường
nhạy
0.
Đường
sức
dòng
trường
đạo
trình
là
những
vòng
tròn
đồng
tâm
quang
trục
đối
xứng.
Để
minh
họa
điều
này,
hình
vẽ
chỉ
ra
ba
đường
sức
thể
hiện
mật
độ
dòng
100,
200,
và
300
pA/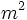 tại
mức
h
=
125mm,
175mm,
và
225mm.
Như
trong
hình
trước,
giá
trị
mật
độ
dòng
trường
đạo
trình
được
tính
từ
dòng
biến
thiên
của
tại
mức
h
=
125mm,
175mm,
và
225mm.
Như
trong
hình
trước,
giá
trị
mật
độ
dòng
trường
đạo
trình
được
tính
từ
dòng
biến
thiên
của
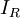 =
1
A/s.
=
1
A/s.
Hiệu quả của bán kính cuộn dây trong đạo trình đơn cực trong mật độ dòng trường đạo trình được chỉ ra trong hình 12.17. Trong hình này, mật độ dòng trường đạo trình được minh họa cho cuộn dây với bán kính 1mm, 10mm, 50mm, 100mm. Dòng điện được đưa vào trong cuộn dây được chuẩn hóa trong quan hệ với vùng cuộn dây để thu được moment lưỡng cực không đổi. Bán kính 10mm được đưa vào với một dòng dI/dt = 1 [A/s].
12.11.3 Hiệu ứng của cuộn dây ở xa với trường đạo trình của đạo trình điểm
Bởi vì tỉ số nhiễu tín hiệu nhỏ của tín hiệu từ sinh học, phép đo thường được tạo ra với một trọng sai kế thứ nhất hoặc thứ hai. Trọng sai kế first-order là một từ kế bao gồm hai cuộn dây đồng trục được tách nhau bởi khoảng cách trung tâm, được gọi là đường cơ sở. Cuộn dây được cuốn vào hướng đối diện. Bởi vì từ trường của nguồn ở xa (nhiễu) được tính trong cả hai cuộn dây, chúng được loại bỏ. Từ trường ở gần với một cuộn dây tạo ra một tín hiệu mạnh trong cuộn dây ở gần gốc (ví dụ.,cuộn dây gần nguồn) hơn là với nguồn ở xa (xa nguồn hơn), và sự khác biệt của những trường này được tìm ra. Độ nhạy trọng sai kế với nguồn bị giảm bớt bởi cuộn dây ở xa bởi số lượng lớn ngắn hơn đường cơ sở. Cuộn dây ở xa cũng làm tăng hiệu ứng lân cận- đó là, độ nhạy của trọng sai kế khác nhau như một hàm của khoảng cách tới nguồn giảm nhanh hơn so với độ nhạy của từ kế một cuộn dây.
Hình 12.18 minh họa mật độ dòng trường đạo trình cho đạo trình đơn cực được tìm ra với những từ kế khác nhau ( víd du.,trọng sai kế). Mật độ dòng trường đạo trình J được minh họa với những đường cơ bản khác nhau như một hàm của khoảng cách r từ trục đối xứng với khoảng cách từ kế h như một tham số. Những từ kế khác nhau có một bán kính cuộn dây là 10mm và một đường cơ sở là 300mm, 150mm, 100mm, 50mm..
Mật độ dòng trường đạo trình của đạo trình lưỡng cực
Như được thảo luận trong phần 12.7 và được minh họa trong hình 12.5, khiđò tìm moment lưỡng cực của một nguồn khối với kich thước lớn hơn so với khoảng cách phép đo, trường đạo trình với vùng nguồn là lý tưởng hơn nhiều nếu một đạo trình lưỡng cực thay thế cho một đạo trình đơn cực được sử dụng. Hình 12.19 chỉ ra mật độ dòng trường đạo trình của một đạo trình lưỡng cực trong một bộ dẫn khối đối xứng trụ được tìm ra với hai từ kế một cuộn dây đồng trục có bán kính cuộn dây là 10mm. Khoảng cách giữa các cuộn dây là 340mm. Chú ý rằng, trong việc sắp xếp trường đạo trình lưỡng cực những cuộn dây được cuốn cùng chiều với nhau và nguồn được đặt ở giữa các cuộn dây. Mật độ dòng trường đạo trình như một hàm của khoảng cách bán kính là thấp nhất trong mặt phẳng đối xứng, ví dụ.,trong mặt phẳng được đặt ở giữa hai cuộn dây. Bởi vì hai cuộn dây bù trừ hiệu ứng lân cận của mỗi cuộn dây khác, mật độ dòng trường đạo trình không thay đổi nhiều như một hàm của khoảng cách từ cuộn dây trong trong mặt phẳng đối xứng gần. Điều này được minh họa với đường đẳng nhạy 500 pA/m2 . Do đó đạo trình lưỡng cực tạo ra một trường đạo trình rất lý tưởng cho việc dò tìm moment lưỡng cực của nguồn khối.
Hình 12.20 minh họa mật độ dòng trường đạo trình với đạo trình lưỡng cực của hình 12.9 với đường đẳng nhạy. Hình vẽ này vẫn chỉ ra rõ ràng hơn so với hình vẽ trước hiệu ứng bù của hai cuộn dây trong mặt phẳng lân cận, nhất là với khoảng cách bán kính ngắn. Dòng trường đạo trình chảy tiếp tuyến xung quanh trục đối xứng. Đường sức được biểu diễn trong hình cới đường liền nét mảnh..
Tham khảo
Abramowitz M, Stegun IA (eds.) (1964): Handbook of Mathematical Functions With Formulas, Graphs, and Mathematical Tables, 1046 pp. Wiley, New York, N.Y. Baule GM, McFee R (1963): Detection of the magnetic field of the heart. Am. Heart J. 55:(7) 95-6. Eskola H (1979): Properties of the unipositional lead system in the measurement of the vector magnetocardiogram. Tampere Univ. Tech., Tampere, Finland, pp. 72. (In Finnish) (Master's thesis) Eskola H (1983): On the properties of vector magnetocardiographic leads. Tampere Univ. Tech., Tampere, Finland, Thesis, pp. 154. (Dr. tech. thesis) Eskola HJ, Malmivuo JA (1983): Optimizing vector magnetocardiographic lead fields by using physical torso model. Il Nuovo Cim. 2:(2) 356-67. Estola K-P, Malmivuo JA (1982): Air-Core induction coil magnetometer design. J. Phys. E.: Sci. Instrum. 15: 1110-3. Faraday M (1834): Experimental researches on electricity, 7th series. Phil. Trans. R. Soc. (Lond.) 124: 77-122. Geselowitz DB (1970): On the magnetic field generated outside an inhomogeneous volume conductor by internal current sources. IEEE Trans. Magn. MAG-6:(2) 346-7. Jackson JD (1975): Classical Electrodynamics, 2nd ed., 84 pp. John Wiley, New York. Malmivuo JA (1976): On the detection of the magnetic heart vector - An application of the reciprocity theorem. Helsinki Univ. Tech., Acta Polytechn. Scand., El. Eng. Series. Vol. 39., pp. 112. (Dr. tech. thesis) Malmivuo JA (1980): Distribution of MEG detector sensitivity: An application of reciprocity. Med. & Biol. Eng. & Comput. 18:(3) 365-70. Malmivuo JA, Lekkala JO, Kontro P, Suomaa L, Vihinen H (1987): Improvement of the properties of an eddy current magnetic shield with active compensation. J. Phys. E.: Sci. Instrum. 20:(1) 151-64. Morse PM, Feshbach H (1953): Methods of Theoretical Physics. Part I, 997 pp. McGraw-Hill, New York. Plonsey R (1972): Capability and limitations of electrocardiography and magnetocardiography. IEEE Trans. Biomed. Eng. BME-19:(3) 239-44. Plonsey R (1982): The nature of sources of bioelectric and biomagnetic fields. Biophys. J. 39: 309-19. Plonsey R, Collin R (1961): Principles and Applications of Electromagnetic Fields, 554 pp. McGraw-Hill, New York. Rush S (1975): On the interdependence of magnetic and electric body surface recordings. IEEE Trans. Biomed. Eng. BME-22: 157-67. Smythe WR (1968): Static and Dynamic Electricity, 3rd ed., 623 pp. McGraw-Hill, New York. Stratton JA (1941): Electromagnetic Theory, McGraw-Hill, New York. Williamson SJ, Romani G-L, Kaufman L, Modena I (eds.) (1983): Biomagnetism: An Interdisciplinary Approach. NATO ASI Series, Series A: Life Sciences, Vol. 66, 706 pp. Plenum Press, New York.
| Trang trước | Lý thuyết của các phép đo từ sinh học | Trang tiếp |