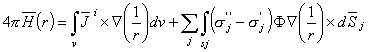Sách:Điện từ sinh học/Từ não đồ

MÁY GHI TỪ NÃO

14.1. Não như là một máy phát từ y sinh

Những điều kiện đầu:

Nguồn: phân bố của nguồn dòng đặt vào bộ phận ⁱ (khối nguồn)

Vật dẫn: hữu hạn, không đồng nhất với sự đối xứng cầu.

Dòng điện sinh học đặt vào có mật độ là ⁱ được liên kết với não bộ hoạt hóa sản sinh điện trường và từ trường. Từ trường được xác định bởi phương trình 12.6.

(14.01)

Đây được gọi là tín hiệu từ não đồ (MEG). David Cohen là người đầu tiên thành công trong việc tìm ra nhịp alpha từ tính. Trong thí nghiệm thành công đầu tiên này ông đã sử dụng máy đo cảm ứng từ trong một phòng che chắn từ tính (Cohen, 1968). David Cohen cũng chính là nhà khoa học đầu tiên phát hiện ra MEG với sự tiếp xúc điểm rf-SQUID vào năm 1970 (Cohen, 1972). Biên độ tín hiệu MEG nhỏ hơn 0.5 pT và có dải tần gần giống như của tín hiệu điện não đồ EEG. Bởi vì trong não bộ thì nguồn sinh ra từ trường giống như nguồn sinh ra điện trường với dòng đặt vào ⁱ , những trường này có hình dạng rất giống nhau.

Cần lưu ý một lần nữa rằng toán hạng đầu tiên ở bên phải của phương trình 12.6 cho thấy sự có mặt của nguồn điện sinh học, trong khi đó toán hạng thứ hai mô tả tính không đồng nhất của bộ dẫn khối. Người đọc có thể dễ dàng xác minh điều này bởi việc thực hiện cái đó trong một vật dẫn đồng tính. Độ dẫn là cân bằng trên cả hai bên của bề mặt phân cách trong từng khoảng nhỏ đồng nhất mô tả bởi phương trình 12.6 và hiệu số (σ”i-σ’i) bằng 0.

Trong tình huống là trụ đối xứng, các trường dòng dẫn sẽ không cắt ngang qua mặt tiếp phân cách của vùng đồng nhất trong từng khoảng đồng nhất của bộ dẫn khối và vì thế không bị ảnh hưởng bởi những tính không đồng nhất ( cầu đối xứng là trường hợp đặc biệt của trụ đối xứng). Công thức toán học này được chỉ báo bởi thực tế là biểu thức thứ hai bên phải của phương trình 12.6 không kể đến điện áp dẫn VLM. Đó là lý do mà trong việc đánh giá phương trình 12.2 chúng ta phải thiết lập tích số điểm của nguồn thứ hai (theo hướng xuyên tâm) với trường đầu ra ( hướng vòng tròn) và có kết quả bằng 0.

Nguồn của tín hiệu MEG, cũng giống với tín hiệu EEG, đó là điện hoạt tính điện của não.Tuy nhiên, như đã thảo luận ở chương 12, sự phân bố độ nhạy của các phép đo từ tính khác với bản chất từ điện bởi vì mật độ dòng dẫn kích thích là _LM và _LE có bản chất khác nhau về hình dạng.

Như ở chương 12, nếu các điện cực của dây dẫn điện nằm ở trên khối dẫn hình cầu ( cái đầu ) và được giữ trên trục đối xứng của dây dẫn từ, các trường dẫn điện và dẫn từ trực giao ở khắp mọi nơi trong khối dẫn, (Malmivuo, 1980; see also Figure 12.2). Trong trường hợp đặc biệt này, MEG như vậy cho phép tìm ra nguồn cấu thành nó mà không thể thấy được với EEG. Điều quan trọng cần lưu ý rằng khi độ nhạy của dây dẫn từ được định hướng tiếp tuyến, tính dẫn kém của sọ không tác động tới hình dạng của trường dẫn.

14.2. Sự phân bố dộ nhạy của các dây dẫn MEG

14.2.1 Phương pháp tính độ nhạy

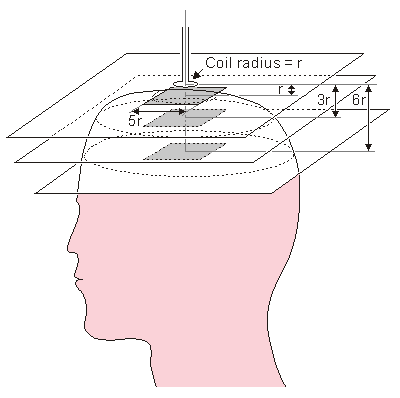
Trong ghi điện não thì cái đầu được mô hình theo những hình cầu đồng tâm.Như đã thảo luận ở trên, mô hình này rất có giá trị và quan trọng cả trong ghi từ não. Vì mức tín hiệu thấp của MEG, các phép đo được thực hiện làm sao càng gần cái đầu nhất có thể. Khi độ nhạy suy giảm nhanh chóng theo khoảng cách, và khi máy dò ống xoắn bán kính nhỏ so với kích thước đầu, cái đầu được mô hình thành công như một nửa không gian.Cái này được chứa đựng trong máy dò MEG đa kênh, vì những máy dò này thường được đặt ở trên bề mặt hình cầu., đồng tâm với đầu.

Có hai cách khác nhau để xây dựng máy dò ống xoắn. Một cách là xây dựng máy dò kênh từ dụng cụ đo trọng sai bậc 1 và bậc 2, ở đây hai hoặc ba máy đo trọng sai cuộn được định vị đồng tâm với đường dây gốc trên các bậc xentimet. Cách khác là sử dụng dụng cụ đo trọng sai phẳng, hai máy dò ống xoắn kế tiếp nhau, được định vị trên cùng mặt phẳng và được kết nối giống như hình dạng ở hình 8.

Như giải thích trong mục 12.11, sự phân bố độ nhạy của các dây dẫn MEG tính toán theo mô hình bán không gian. Trong trường hợp đa kênh, tổng độ nhạy dễ dàng thu được từ độ nhạy đặt lên riêng mỗi kênh. Sự phân bố độ nhạy được minh họa trên mặt phẳng, được định hướng song song với bề mặt ngoài của đầu, và định vị ở những khoảng cách khác nhau, minh họa như hình 14.1. Máy dò ống xoắn định vị song song với bề mặt và có bán kính r. Với giả định là tất cả các ống xoắn đều định vị trên cùng mặt phẳng. Phương pháp này trong trường hợp máy dò đơn ống xoắn gọi là một máy đo độ dốc xoắn ốc. Trong trường hợp ống xoắn kẹp máy dò tương đương với một máy đo độ dốc hai chiều bậc 1.

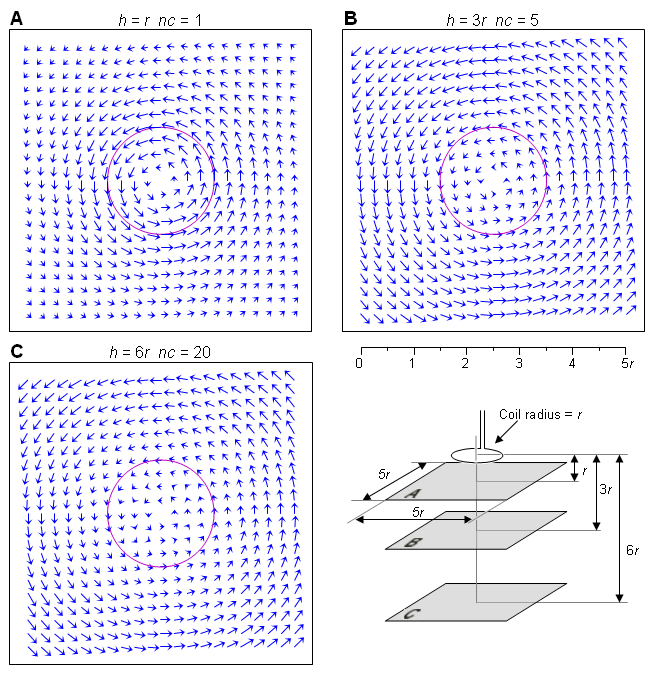
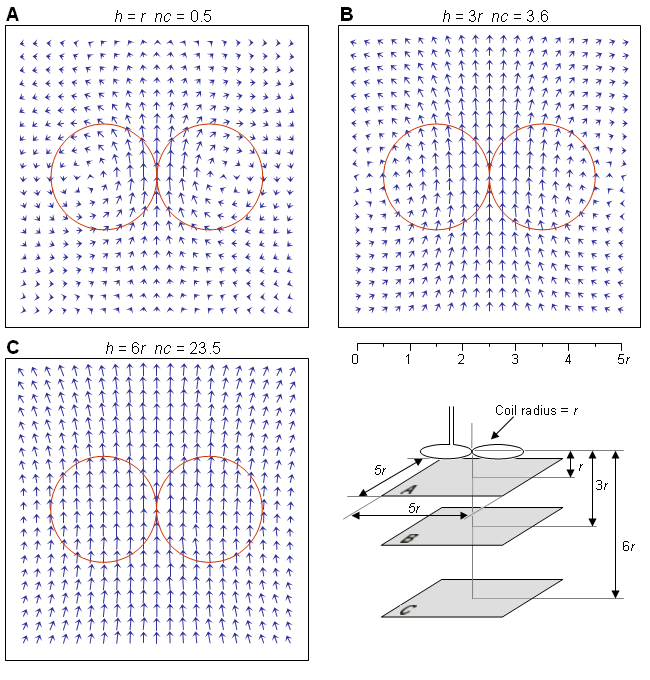
Những trường dẫn được minh họa như các trường vectơ (Malmivuo and Puikkonen, 1987, 1988). Sự minh họa này được chuẩn hóa để khoảng cách của những mặt phẳng là 1r, 3r, 6r, ở đây r là bán kính của máy đo độ dốc ống xoắn. Hầu hết độ xa của những mặt phẳng này (6r) là chính xác khi đánh giá các trường dẫn cho máy dò ống xoắn nhỏ MEG và tiến dần tới 1 (1r) khi áp dụng sự kích thích từ tính với ống xoắn lớn. Trường dẫn chỉ biểu diễn trên một mặt phẳng bên trong hình vuông có kích thước mặt chính là 6r. Trong mỗi hình các trường vectơ được chuẩn hóa thành vecto cực đại có độ lớn xấp xỉ kích thước chuẩn. Sự chuẩn hóa hệ số nc xác định ở mỗi hình trong mối quan hệ của hình 14.2A, nó minh họa trường dẫn của ống xoắn đơn trên một mặt phẳng có khoảng cách là 1r từ ống xoắn.

Những trường dẫn này minh họa cả các trường vecto dẫn và các dòng đẳng nhạy. Đẳng nhạy dòng minh họa khối bán nhạy cũng được xuất hiện.Khái niệm này miêu tả không gian độ nhạy bằng hoặc hơn một nửa của độ nhạy cực đại. Xét khối bán nhạy nhỏ nhất , chính xác hơn nó có thể tìm ra các tín hiệu từ những vùng khác nhau của khối nguồn.

Hình 14.1. Vị trí của các mặt phẳng trong việc đánh giá sự phân bố độ nhạy của hệ thống dây dẫn MEG.

14.2.2. Từ kế đơn cuộn

Điều kiện đầu

Nguồn: từ kế đơn cuộn

Vật dẫn: hữu hạn, tính không đồng nhất với đối xứng cầu dọc theo trục từ kế

Sự phân bố độ nhạy của từ kế đơn cuộn được minh họa ở hình 14.2. Sự phân bố độ nhạy có hình dạng là các đường tròn đồng tâm ở khắp khối dẫn cầu. Ở khoảng cách có độ lớn 1r độ nhạy tăng theo một hàm của khoảng cách từ trục tới đỉnh đầu. Trên hai mặt phẳng xa hơn độ nhạy cực đại là một hàm của bán kính mà không thấy được trong vùng minh họa.

Đó là điều lưu ý để so sánh hình 14.2 và 12.15. Giống như đã chú thích ở chương 12, những hình này miêu tả sự phân bố độ nhạy giống nhau minh họa của các phương pháp khác nhau. Người đọc sẽ phải thừa nhận rằng, đường cong ở hình 12.15 tương đương với sự biến đổi chiều dài của các vecto trong hình 14.2 và như thế chúng miêu tả trường dẫn như là một hàm của bán kính.

Như chú ý trước, chiều dài của các vecto trong hình 14.2B và 14.2C tăng lên nhiều lần bởi sự chuẩn hóa hệ số nc vì vậy mà trong mỗi hình thì chiều dài cực đại của các vécto là xấp xỉ bằng nhau.

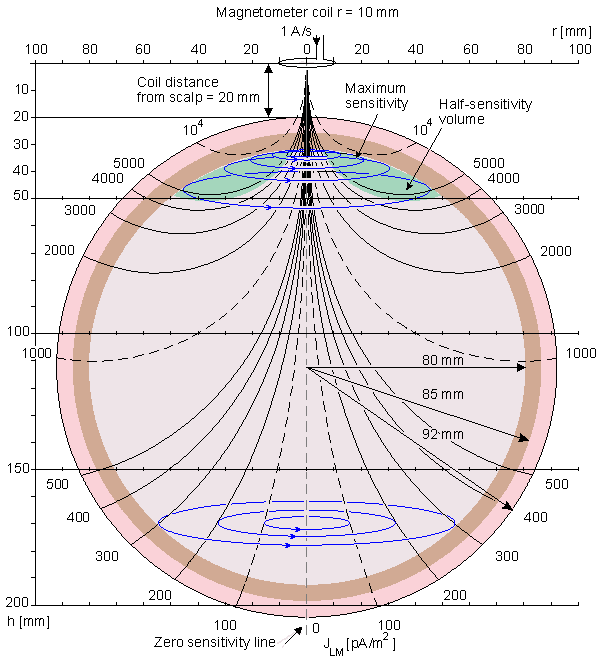
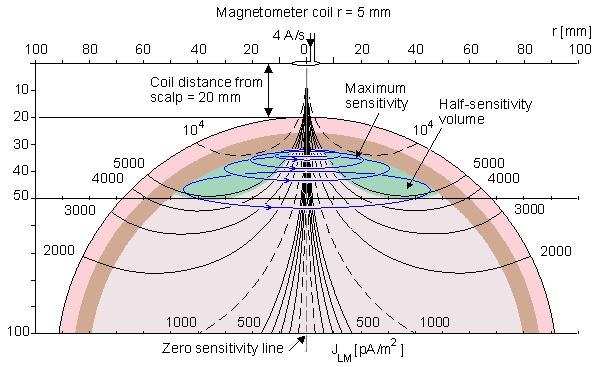
Hình 14.3A và B minh họa sự phân bố độ nhạy với các dòng đẳng nhạy cho từ kế đơn cuộn với bán kính tương ứng là 10mm và 5mm. Các dòng đẳng nhạy nối liền các điểm trong không gian nơi mà mật độ dòng dẫn kích thích có cùng giá trị.Các dòng đẳng nhạy minh họa bằng các đường đứt nét. Trong hình còn minh họa vài lưu lượng dòng dẫn kích thích bằng các đường liền mảnh. Bởi vì trường dẫn của từ kế đơn cuộn biểu hiện là đối xứng trụ, mô hình đầu phồng tròn có hướng xếp chồng lên hình này. Điều đó cho thấy rằng khoảng cách từ ống xoắn đến da đầu là 20mm.Sự phân bố độ nhạy của một ống xoắn với bán kính 50mm trình bày sự kết nối trễ với kích thích của từ tính trong hình14.4

Những vùng với độ nhạy cực đại và khối bán nhạy được đánh bóng rõ rệt.Vị trí của các vùng độ nhạy cực đại và kích cỡ của khối bán nhạy phụ thuộc vào khoảng cách đo và bán kính ống xoắn, thế nhưng mối quan hệ này là không bền vững.

Hình 14.2 Sự phân bố độ nhạy của một từ kế đơn cuộn có bán kính r. Sự phân bố độ nhạy được đưa ra bởi ba mặt phẳng song song với khoảng cách là (A) 1r, (B) 3r, (C) 6r. Chú ý rằng chiều dài của các véc tơ tại B và C tăng lên gấp nhiều lần bởi sự chuẩn hóa hệ số nc.

Hình 14.3. Các dòng đẳng nhạy trong phép đo MEG của mô hình cầu phồng tròn với từ kế đơn cuộn có bán kính là A, 10mm và B, 5mm. Độ nhạy ở khắp nơi có định hướng tiếp xúc tới trục đối xứng nó là dòng có độ nhạy 0. Trong vùng không gian não thì độ nhạy cực đại ở vị trí bề mặt của não và nó chỉ thị sự đánh bóng.

14.2.3. Dụng cụ đo trọng sai phẳng.

Điều kiện đầu:

Nguồn: dụng cụ đo trọng sai phẳng.

Vật dẫn: dẫn điện bán không gian

Sự phân bố độ nhạy của một dụng cụ đo trọng sai được minh họa ở hình 14.4. Từ hai ống xoắn kế tiếp nhau, ở bên trái là vết thương theo định hướng tích cực, ở bên phải tương ứng theo hướng tiêu cực ( cái sau được rút ra bằng các đường đứt nét).Cấu trúc này được gọi là dụng cụ đo trong sai phẳng. Vị trí của phép đo này làm sao để đạt tốt nhất bởi những tín hiệu đo suy giảm do hai từ kế liền nhau hoặc (trục) dụng cụ đo trọng sai.

Sự phân bố độ nhạy của dụng cụ đo trọng sai phẳng không dài hơn đường tròn chính nhưng có dạng tiếp tuyến trong vùng đích. Mặt phẳng đo ở phía xa hơn là do máy dò ống xoắn, sự phân bố độ nhạy là đồng nhất hơn. Độ lớn của độ nhạy trong dụng cụ đo trọng sai phẳng giảm nhanh hơn so với trong từ kế đơn cuộn theo một hàm của khoảng cách. Bởi vậy, dò tìm những tín hiệu phát ra từ vị trí nguồn chính trong vùng tiến gần đến máy dò.

Cần chú ý rằng sự phân bố độ nhạy của phép đo lưỡng cực điện cũng theo chiều dài, giống như hình 13.4. Như vậy sự phân bố độ nhạy của dụng cụ đo trọng sai phẳng MEG là tương tự như phép đo lưỡng cực EEG.

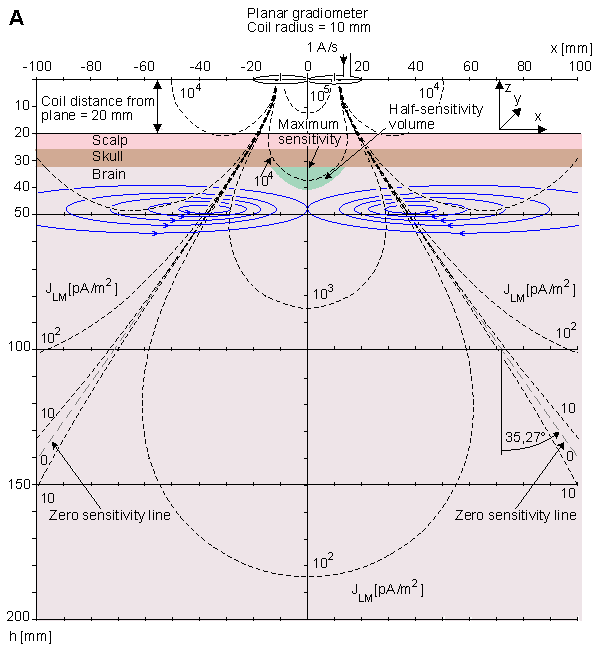
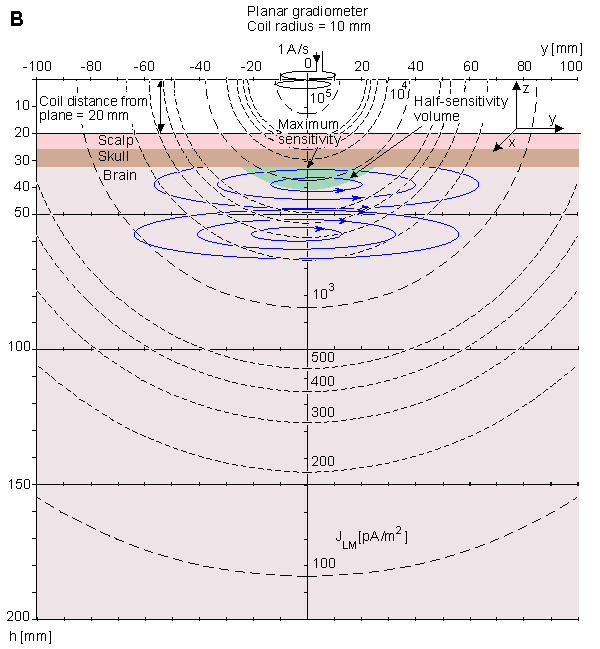
Những dòng đẳng nhạy của dụng cụ đo trọng sai phẳng được minh họa ở hình 14.5. Bởi vì từ kế này được bố trí và trường dẫn nó không tạo ra trụ đối xứng, những kết quả là chính xác chỉ tại vô cùng, khối dẫn đồng nhất hoặc đồng nhất bán không gian. Vì vậy, mô hình đầu phồng tròn không thể xếp chồng lên những minh họa này và mô hình dẫn điện bán không gian được sử dụng. Khoảng cách của bán không gian được lựa chọn giống như trong mô hình đầu phồng tròn theo hướng xuống dưới ống xoắn. Hình 14.5 A minh họa những dòng đẳng nhạy trong mặt phẳng xz, nó là mặt phẳng bao gồm hệ trục của các ống xoắn. Mặt phẳng này bao gồm cả dòng có độ nhạy 0. Nó như một dòng tạo thành góc 35.27° với trục z. Hình 14.5 B minh họa các dòng đẳng nhạy trong mặt phẳng yz. Trong mặt phẳng này dòng đẳng nhạy là các đường tròn đồng tâm có khoảng cách lớn so với kích thước ống xoắn. Ở khoảng cách 10r và 100r chúng khác với trong phạm vi lần lượt là 1% và 0.1% từ một đường tròn. Những đường liền mảnh minh họa lưu lượng dòng dẫn kích thích. Đây là những giải pháp không đúng đắn.

Hình 14.4 Sự phân bố độ nhạy của một dụng cụ đo trọng sai phẳng có bán kính r.Sự phân bố độ nhạy đã cho ba mặt phẳng song song với những khoảng cách (A) 1r, (B) 3r, (C) 6r. Chiều dài của các véc tơ trong các mặt phẳng A,B,C được tăng lên nhiều lần bởi sự chuẩn hóa hệ số nc.

Hình 14.5 Các dòng đẳng nhạy ( những đường đứt nét) và khối bán nhạy của dụng cụ đo trọng sai phẳng để tính toán cho bán không gian dẫn điện. Lưu lượng các dòng dẫn kích thích được biểu diễn bằng những đường liền mảnh Chúng là những giải pháp không đúng đắn.

A. Trong mặt phẳng xz, dòng độ nhạy 0 bắt đầu tiếp cận dòng nó tạo thành góc 35.27° với trục z.

B. Trong mặt phẳng yz, dòng độ nhạy tiến gần đường tròn đồng tâm với khoảng cách đáng kể đến các đường tròn đồng tâm.

14.3. Sự so sánh giữa EEG và MEG - khối bán nhạy.

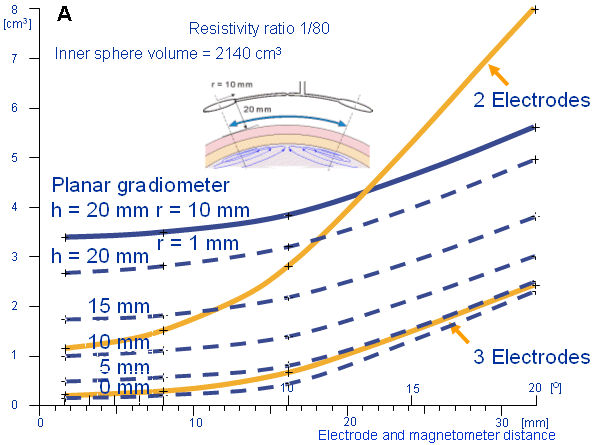
Trong những thảo luận trước đây, sự đánh giá về khối bán nhạy là một hình có ưu điểm mô tả hệ thống dẫn có khả năng làm tăng chất lượng phép đo độ nhạy. Suihko and Malmivuo (1993) so sánh khối bán nhạy (trong vùng não) của hai và ba dây dẫn điện cực và của theo hướng dọc trục và dụng cụ đo trọng sai phẳng dây dẫn từ như một hàm của khoảng cách điện cực/ dây dẫn gốc dụng cụ đo trọng sai. Những dây dẫn điện và từ được mô tả lần lượt ở trong hình 13.4 và trong hình 14.3 và 14.5. Khi bổ sung thêm vào đó ba điện cực dẫn đánh giá ở đây là tất cả các điện cực đều nhau, một bên sẽ liên hệ để xử lý như thiết bị đầu cuối khác. Mô hình đầu là mô hình phồng tròn của Rush and Driscoll (1969). Kết quả được minh họa trong hình 14.6.

Tất cả những dây dẫn này, như một sự kì vọng, khối bán nhạy nhỏ nhất với khoảng cách điện cực nhỏ/ dây dẫn gốc dụng cụ đo trọng sai. Dây dẫn điện có giá trị nhỏ nhất sẽ tốt hơn những dây dẫn từ.Khối bán nhạy với ba điện cực dẫn ở 1° khoảng cách là 0.2 cm³,và với hai điện cực dẫn là 1.2 cm³. Khối bán nhạy với hai điện cực dẫn chỉ đạt 30% của dụng cụ đo trọng sai phẳng (3.4 cm³), trong khi đó của dụng cụ đo trọng sai hướng trục là 21.8 cm³. Dụng cụ đo trọng sai đưa ra kết quả tính toán là 20mm khoảng cách từ ống xoắn đến da đầu.

20mm khoảng cách ống xoắn và 10mm bán kính ống xoắn thực hiện giống như cái mũ bảo vệ đầu khi dung máy dò MEG. Tuy nhiên, các dụng cụ đo MEG dùng để ghi lại một vùng có hạn nơi mà khoảng cách ống xoắn và bán kính ống xoắn dưới 1mm. Bởi vậy minh họa ở hình 14.6 của nó là khối bán nhạy cho dụng cụ đo trọng sai phẳng với 1mm bán kính ống xoắn ở 0- 20mm khoảng cách ghi. Những đường cong thể hiện này, khi khoảng cách ghi khoảng 12mm thì dụng cụ đo trọng sai phẳng giống với khối bán nhạy và như là EEG hai điện cực.

Ở khía cạnh khác, sự so sánh của dây dẫn điện và dây dẫn từ là dạng của sự phân bố độ nhạy. Với khoảng cách điện cực ngắn/ dây dẫn gốc những trường dẫn trong hai điện cực và dụng cụ đo trọng sai phẳng dây dẫn tiếp xúc chính với đầu, như minh họa lần lượt ở hình 13.4 (khoảng cách điện cực ở 20° và 40°) và hình 14.4. Ba điện cực dẫn có nền tảng là sự phân bố độ nhạy hướng tâm ( không minh họa trong sách) và dụng cụ đo trọng sai hướng trục có phân bố độ nhạy như luồng lốc xoáy (tiếp xúc với trục đối xứng của dụng cụ đo trọng sai) thấy ở hình 14.2 và 14.3.

Tóm lại, trong thực tế những điều kiện đo là khác nhau giữa hai điện cực dẫn EEG và dụng cụ đo trọng sai phẳng dây dẫn MEG trong kích cỡ của khối bán nhạy và dạng phân bố độ nhạy rất nhỏ. Đây là những kết quả quan trọng bởi vì nó tổng quát được rằng điện trở suất cao của điện cực dẫn với lực tác động hôp sọ để ghi lại tín hiệu tại những vùng lớn. Tuy nhiên đây không phải là trường hợp quyết định nhưng hai điện cực EEG dụng cụ đo trọng sai phẳng MEG hiệu quả gần như nhau trong những bộ nhạy đồng tâm, trong khi dây dẫn điện ba điện cực có hiệu quả lớn hơn.

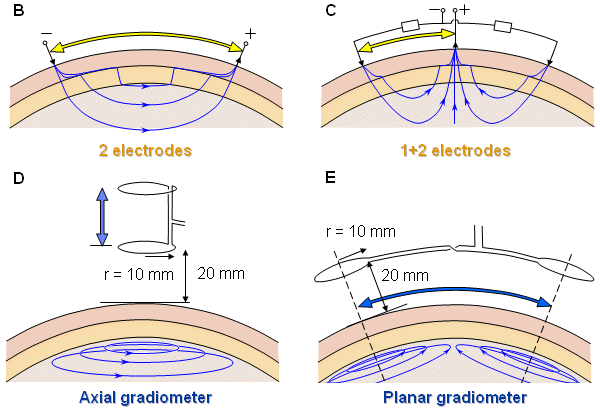
Hình 14.6 (A) Khối bán nhạy với hai và ba điện cực dẫn (những dòng màu vàng), dụng cụ đo trọng sai phẳng có bán kính ống xoắn 10mm (dòng màu xanh lam) và bán kính 1mm (màu xanh lam đứt nét) như một hàm khoảng cách điện cực/ dây dẫn gốc dụng cụ đo trọng sai.

Những vị trí đo thể hiện ở hình (B) cho hai điện cực và (C) cho dây dẫn điện ba điện cực, (D) cho dụng cụ đo trọng sai hướng trục, (E) cho dụng cụ đo trọng sai phẳng. Mô hình đầu là mô hình cầu đồng nhất của Rush and Driscoll. (Suihko and Malmivuo, 1993).

14.4. Tổng kết

Trong chương này, sự phân bố độ nhạy được tính toán cho một hoặc nhiều kênh của máy dò MEG. Phương pháp sử dụng trong chương này là hợp lý của đối xứng trụ dưới các điều kiện. Đây là sự xấp xỉ chính xác khi thực hiện các tại vị trí đo MEG. Có phương pháp khác để tính toán sự phân bố độ nhạy của máy dò MEG đó là đưa ra kết quả chính xác tại những vị trí kém đối xứng; bởi vậy chúng sẽ phức tạp hơn, và đáng tiếc, không có nhiều minh họa về nó (Eaton, 1992; Esselle and Stuchly, 1992).

Nếu hai cuộn kế tiếp được kết nối với nhau hoặc trực tiếp phù hợp với kết luận về những tín hiệu tìm ra để mà dò tìm ống xoắn trong từ trường theo hướng khác nhau, hoặc kết hợp thành những ống xoắn dạng dụng cụ đo trọng sai phẳng. Sự phân bố độ nhạy xây dựng như vậy không còn là vòng tròn (lốc xoáy) nhưng tuyến tính và rất giống với một dây dẫn điện. Độ nhạy cực đại và, bởi thế, chắc hẳn hầu hết vị trí của tín hiệu nguồn được xây dựng là vị trí trực tiếp ngay dưới ống xoắn ( với sự đối xứng).

Đó là sự khác biệt của máy dò đa kênh MEG. Số kênh tăng từ 7 (Knuutila et al., 1987) đến 24 (Kajola et al., 1990) và 32 (Hoenig et al., 1989) đến 124 (Knuutila et al., 1991). Máy dò nhiều cuộn thường đặt ở vị trí trên mặt phẳng cầu đối xứng với đầu. Trên mặt phẳng này những ống xoắn thường được đặt có thề gần giống nhau, mô hình giống hình tổ ong. Trong 124 kênh đã xây dựng vỏ bọc cách nhiệt cho đầu cấu trúc mũ bảo vệ.

Trong từ trường số lượng véc tơ (không giống trường điện thế là số lượng vô hướng) đa số trong máy dò ghi MEG chỉ cấu thành nên từ trường. Lại có, tuy nhiên, một vài chi tiết ở đây là cả ba thành phần của từ trường đều được ghi lại. Khởi đầu, công việc tiên phong của ông, David Cohen minh họa dạng véc tơ của từ trường trong não (Cohen, 1972). Như thí dụ, sự nghiên cứu MEG hiện đại với véc tơ dụng cụ đo dung sai của Yoshinori Uchikawa và các bạn đồng nghiệp của ông cũng đã tiếp tục đề cập đến (Uchikawa et al., 1992; 1993).

Trong MEG điều quan tâm chính của chúng ta là điện hoạt động trên bề mặt của não, vỏ não. Vì vậy phép đo đơn cực là chính xác khi đo MEG. Như sẽ thảo luận ở chương 20, trong MCG của chúng ta nó liên quan đến điện hoạt động trong tổng thể cơ tim. Vì vậy, phép đo lưỡng cực ( đối xứng) có liên quan nhiều đến phép đo MCG.

Tham khảo

• Cohen D (1968): Magnetoencephalography, evidence of magnetic fields produced by alpha-rhythm currents. Science 161: 784-6.
• Cohen D (1972): Magnetoencephalography: Detection of brain's electric activity with a superconducting magnetometer. Science 175:(4022) 664-6.
• Eaton H (1992): Electric field induced in spherical conductor from arbitrary coils: Application to magnetic stimulation and MEG. Med. & Biol. Eng. & Comput. 30:(July) 433-40.
• Hoenig HE, Daalmans G, Folberth W, Reichenberger H, Schneider S, Seifert H (1989): Biomagnetic multichannel system with integrated squids and first order gradiometers operating in a shielded room. Cryogenics 29:(8) 809-13.
• Kajola M, Ahlfors S, Ehnholm GJ, Hällström J, Hämäläinen MS, Ilmoniemi RJ, Kiviranta M, Knuutila J, Lounasmaa OV, Tesche CD, Vilkman V (1990): A 24-channel magnetometer for brain research. In Advances in Biomagnetism, ed. SJ Williamson, L Kaufman, pp. 673-6, Plenum Press, New York.
• Knuutila J, Ahlfors S, Ahonen A, Hällström J, Kajola M, Lounasmaa OV, Tesche C, Vilkman V (1987): A large-area low-noise seven-channel dc-squid magnetometer for brain research. Rev. Sci. Instrum. 58: 2145-56.
• Knuutila J, Ahonen A, Hämäläinen M, Kajola M, Lounasmaa OV, Simola J, Tesche C, Vilkman V (1991): Design of a 122-channel neuromagnetometer covering the whole head. In Abst. 8th Internat. Conf. Biomagnetism, ed. M Hoke, pp. 109-10, Westfälische Wilhelms-Universität, Münster.
• Malmivuo JA (1980): Distribution of MEG detector sensitivity: An application of reciprocity. Med. & Biol. Eng. & Comput. 18:(3) 365-70.
• Malmivuo JA, Puikkonen J (1987): Sensitivity distribution of multichannel MEG detectors. In Abst. 6th Internat. Conf. Biomagnetism, Tokyo, 27-30 August, ed. K Atsumi, M Kotani, S Ueno, T Katila, SJ Williamson, pp. 112-3, Tokyo Denki University Press, Tokyo.
• Malmivuo JA, Puikkonen J (1988): Qualitative properties of the sensitivity distribution of planar gradiometers. Tampere Univ. Techn., Inst. Biomed. Eng., Reports 2:(1) pp. 35.
• Rush S, Driscoll DA (1969): EEG-electrode sensitivity - An application of reciprocity. IEEE Trans. Biomed. Eng. BME-16:(1) 15-22.

Các sách tham khảo:

• Hoke M, Grandori F, Romani G-L (eds.) (1990): Auditory Evoked Magnetic Fields and Electric Potentials, 362 pp. S. Karger, Basel.
• Regan D (1989): Human Brain. Electrophysiology, Evoked Potentials and Evoked Magnetic Fields in Science and Medicine, 672 pp. Elsevier, Amsterdam.
• Suihko V, Malmivuo J (1993): Sensitivity distributions of EEG and MEG measurements. In EEG and MEG Signal Analysis and Interpretation, Proceedings of the Second Ragnar Granit Symposium, ed. J Hyttinen, J Malmivuo, pp. 11-20, Tampere University of Technology, Ragnar Granit Institute, Tampere.
• Swithenby SJ (1987): Biomagnetism and the biomagnetic inverse problem. Phys. Med. Biol. MJ Day (ed.): The Biomagnetic Inverse Problem, 32:(1) 146. (Papers from a conference at the Open University, April 1986).
• Uchikawa Y, Matsumura F, Kobayashi K, Kotani M (1993): Discrimination and identification of multiple sources of the magnetoencephalogram using a three-dimensional second-order gradiometer. J. Jpn. Biomagn. Bioelectromagn. Soc. 6: 12-5.

---

Trang trước

Từ não đồ

Trang tiếp

Liên kết đến đây

• Sách:Điện từ sinh học
• Sách:Điện từ sinh học/Điện não đồ
• Sách:Điện từ sinh học/Đo điện và từ trường của hoạt động điện của tim