Chủ đề nóng: Phương pháp kỷ luật tích cực - Cổ học tinh hoa - Những thói hư tật xấu của người Việt - Công lý: Việc đúng nên làm - Giáo án Điện tử - Sách giáo khoa - Học tiếng Anh - Bài giảng trực tuyến - Món ăn bài thuốc - Chăm sóc bà bầu - Môi trường - Tiết kiệm điện - Nhi khoa - Ung thư - Tác hại của thuốc lá - Các kỹ thuật dạy học tích cực
- Dạy học phát triển năng lực - Chương trình giáo dục phổ thông
Tìm phương trình tiếp tuyến
Từ VLOS
Khác với đường thẳng, hệ số góc (độ dốc) liên tục thay đổi khi di chuyển dọc đường cong. Tích phân đưa ra ý tưởng mỗi điểm trên đồ thị có thể được diễn tả bằng một hệ số góc hay "tốc độ thay đổi liên tục". Đường tiếp tuyến tại một điểm là đường thẳng có cùng hệ số góc và đi qua chính điểm đó. Để tìm phương trình đường tiếp tuyến, bạn cần biết cách lấy đạo hàm phương trình ban đầu.
Mục lục
Các bước[sửa]
Tìm phương trình đường tiếp tuyến[sửa]
-
Vẽ
hàm
và
đường
tiếp
tuyến
(bước
này
không
bắt
buộc
nhưng
nên
thực
hiện).
Biểu
đồ
sẽ
giúp
bạn
dễ
dàng
hơn
trong
việc
hiểu
đề
và
kiểm
tra
liệu
đáp
án
có
hợp
lý
hay
không.
Vẽ
hàm
số
trên
giấy
kẻ
ô,
sử
dụng
máy
tính
khoa
học
có
chức
năng
vẽ
đồ
thị
để
tham
khảo
nếu
cần.
Vẽ
đường
tiếp
tuyến
đi
qua
điểm
cho
trước
(Nhớ
rằng
đường
tiếp
tuyến
đi
qua
điểm
đó
và
có
cùng
hệ
số
góc
với
đồ
thị
tại
đó).
-
Ví
dụ
1:
Vẽ
parabol
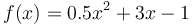 .
Vẽ
đường
tiếp
tuyến
đi
qua
điểm
(-6,
-1).
.
Vẽ
đường
tiếp
tuyến
đi
qua
điểm
(-6,
-1).
Dù chưa biết phương trình tiếp tuyến nhưng bạn vẫn có thể thấy rằng hệ số góc của nó là âm và tung độ gốc bé hơn 0 (nằm xa dưới đỉnh parabol với tung độ bằng -5,5). Nếu đáp án cuối cùng tìm được không phù hợp với những chi tiết này, chắc hẳn có lỗi trong tính toán và bạn cần kiểm tra lại.
-
Ví
dụ
1:
Vẽ
parabol
-
Lấy
đạo
hàm
bậc
nhất
để
tìm
phương
trình
hệ
số
góc
của
đường
tiếp
tuyến.
Với
hàm
số
f(x),
đạo
hàm
bậc
nhất
f'(x)
đại
diện
phương
trình
hệ
số
góc
của
đường
tiếp
tuyến
tại
mọi
điểm
trên
f(x).
Có
rất
nhiều
cách
để
đạo
hàm.
Đây
là
một
ví
dụ
đơn
giản
sử
dụng
quy
tắc
lũy
thừa:[1]
-
Ví
dụ
1
(tt):
Đồ
thị
được
cho
bởi
hàm
số
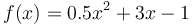 .
.
Nhắc lại quy tắc lũy thừa khi lấy đạo hàm: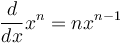 .
.
Đạo hàm bậc nhất của hàm số = f'(x) = (2)(0.5)x + 3 - 0.
f'(x) = x + 3. Thay x bằng bất kỳ giá trị a nào, phương trình sẽ cho ta hệ số góc của đường tiếp tuyến hàm số f(x) tại điểm x = a.
-
Ví
dụ
1
(tt):
Đồ
thị
được
cho
bởi
hàm
số
-
Nhập
giá
trị
x
của
điểm
đang
xét.
Đọc
đề
để
tìm
tọa
độ
của
điểm
cần
tìm
đường
tiếp
tuyến.
Nhập
hoành
độ
của
điểm
này
vào
f’(x).
Kết
quả
thu
được
là
hệ
số
góc
của
đường
tiếp
tuyến
tại
điểm
trên.
-
Ví
dụ
1
(tt):
Điểm
được
đề
cập
trong
đề
là
(-6,
-1).
Dùng
hoành
độ
-6
thế
vào
f’(x):
f'(-6) = -6 + 3 = -3
Hệ số góc của đường tiếp tuyến là -3.
-
Ví
dụ
1
(tt):
Điểm
được
đề
cập
trong
đề
là
(-6,
-1).
Dùng
hoành
độ
-6
thế
vào
f’(x):
-
Viết
phương
trình
đường
tiếp
tuyến
có
dạng
đường
thẳng
khi
biết
hệ
số
góc
và
một
điểm
nằm
trên
nó.
Phương
trình
tuyến
tính
này
được
viết
dưới
dạng
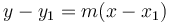 .
Trong
đó,
m
là
hệ
số
góc
và
.
Trong
đó,
m
là
hệ
số
góc
và
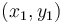 là
một
điểm
trên
đường
tiếp
tuyến.[2]
Bây
giờ,
bạn
đã
có
mọi
thông
tin
cần
thiết
để
viết
phương
trình
đường
tiếp
tuyến
ở
dạng
này.
là
một
điểm
trên
đường
tiếp
tuyến.[2]
Bây
giờ,
bạn
đã
có
mọi
thông
tin
cần
thiết
để
viết
phương
trình
đường
tiếp
tuyến
ở
dạng
này.
-
Ví
dụ
1
(tt):
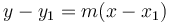
Hệ số góc của đường tiếp tuyến là -3, do đó: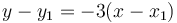
Đường tiếp tuyến đi qua điểm (-6, -1), vì vậy, phương trình cuối cùng là: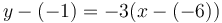
Rút gọn ta được: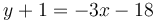
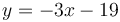
-
Ví
dụ
1
(tt):
-
Xác
nhận
bằng
đồ
thị.
Nếu
có
máy
tính
có
chức
năng
vẽ
đồ
thị,
hãy
vẽ
đồ
thị
hàm
gốc
và
đường
tiếp
tuyến
để
kiểm
tra
liệu
đáp
án
đã
chính
xác
hay
chưa.
Nếu
tính
toán
trên
giấy,
hãy
dùng
đồ
thị
đã
vẽ
trước
đó
để
đảm
bảo
không
có
sai
sót
hiển
nhiên
nào
trong
đáp
án
của
bạn.
- Ví dụ 1 (tt): Hình vẽ ban đầu cho thấy đường tiếp tuyến có hệ số góc âm và tung độ gốc nằm dưới xa so với -5,5. Phương trình tiếp tuyến vừa tìm được là y = -3x -19, nghĩa là -3 là hệ số góc và -19 là tung độ gốc.
-
Thử
giải
quyết
một
bài
toán
khó
hơn.
Chúng
ta
đi
qua
toàn
bộ
các
bước
ở
trên
một
lần
nữa.
Lúc
này,
mục
tiêu
là
tìm
đường
tiếp
tuyến
của
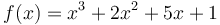 tại
x
=
2:
tại
x
=
2:
-
Tìm
đạo
hàm
bậc
nhất
bằng
quy
tắc
lũy
thừa:
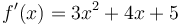 .
Hàm
số
này
sẽ
cho
chúng
ta
hệ
số
góc
của
tiếp
tuyến.
.
Hàm
số
này
sẽ
cho
chúng
ta
hệ
số
góc
của
tiếp
tuyến. -
Với
x
=
2,
tìm
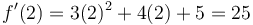 .
Đây
là
hệ
số
góc
tại
x
=
2.
.
Đây
là
hệ
số
góc
tại
x
=
2. -
Lưu
ý
rằng
lần
này,
chúng
ta
không
có
một
điểm
và
chỉ
có
tọa
độ
x.
Để
tìm
tọa
độ
y,
thay
x
=2
vào
hàm
ban
đầu:
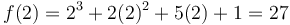 .
Điểm
thu
được
là
(2,27).
.
Điểm
thu
được
là
(2,27). -
Viết
phương
trình
đường
tiếp
tuyến
đi
qua
một
điểm
và
có
hệ
số
góc
xác
định:
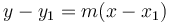
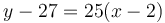
Nếu cần, rút gọn về y = 25x - 23.
-
Tìm
đạo
hàm
bậc
nhất
bằng
quy
tắc
lũy
thừa:
Giải quyết các vấn đề liên quan[sửa]
-
Tìm
điểm
cực
trị
trên
đồ
thị.
Chúng
là
những
điểm
mà
tại
đó,
đồ
thị
tiến
đến
điểm
cực
đại
cục
bộ
(điểm
cao
hơn
những
điểm
lân
cận
ở
cả
hai
bên)
hoặc
điểm
cực
tiểu
cực
bộ
(thấp
hơn
những
điểm
lân
cận
ở
cả
hai
bên).
Đường
tiếp
tuyến
luôn
có
hệ
số
góc
bằng
0
ở
những
điểm
này
(một
đường
thẳng
nằm
ngang).
Tuy
nhiên,
hệ
số
góc
bằng
không
chưa
đủ
để
kết
luận
đó
là
điểm
cực
trị.
Dưới
đây
là
cách
tìm
chúng:[3]
- Lấy đạo hàm bậc nhất của hàm số để có f’(x), phương trình hệ số góc đường tiếp tuyến.
- Giải phương trình f'(x) = 0 để tìm điểm cực trị tiềm năng.
- Lấy đạo hàm bậc hai để có f''(x), phương trình cho chúng ta biết tốc độ thay đổi của hệ số góc đường tiếp tuyến.
- Tại mỗi điểm cực trị tiềm năng, thay hoành độ a vào f''(x). Nếu f''(a) dương, ta có một điểm cực tiểu cục bộ tại a. Nếu f''(a) âm, ta có một điểm cực đại cục bộ. Nếu f''(a) bằng 0, đó không phải cực trị mà là một điểm uốn.
- Nếu đạt cực đại hoặc cực tiểu tại a, tìm f(a) để xác định tung độ.
-
Tìm
phương
trình
đường
pháp
tuyến.
Đường
"pháp
tuyến"
của
một
đường
cong
tại
điểm
xác
định
a
sẽ
đi
qua
điểm
đó
và
vuông
góc
với
đường
tiếp
tuyến.
Để
tìm
phương
trình
đường
pháp
tuyến,
sử
dụng
điều
đã
biết
sau:
(hệ
số
góc
đường
tiếp
tuyến)(hệ
số
góc
đường
pháp
tuyến)
=
-1
khi
chúng
đi
qua
cùng
một
điểm
trên
đồ
thị.[4]
Cụ
thể:
- Tìm f'(x), hệ số góc đường tiếp tuyến.
- Nếu tại điểm đã cho, ta có x = a: tìm f'(a) để xác định hệ số góc tại điểm đó.
-
Tính
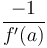 để
tìm
hệ
số
góc
đường
pháp
tuyến.
để
tìm
hệ
số
góc
đường
pháp
tuyến. - Viết phương trình đường pháp tuyến khi biết hệ số góc và một điểm mà nó đi qua.
Lời khuyên[sửa]
- Nếu cần, hãy viết lại phương trình ban đầu dưới dạng chuẩn: f(x) = ... hay y = ...
Nguồn và Trích dẫn[sửa]
- ↑ https://www.mathsisfun.com/calculus/derivatives-rules.html
- ↑ http://gato-docs.its.txstate.edu/jcr:48ee831e-5969-4419-b9f8-820925a1b46a/Finding%20the%20Equation%20of%20a%20Tangent%20Line.pdf
- ↑ http://www.themathpage.com/acalc/max.htm
- ↑ http://revisionmaths.com/advanced-level-maths-revision/pure-maths/calculus/tangents-and-normals


