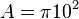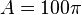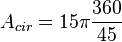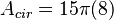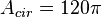Chủ đề nóng: Phương pháp kỷ luật tích cực - Cổ học tinh hoa - Những thói hư tật xấu của người Việt - Công lý: Việc đúng nên làm - Giáo án Điện tử - Sách giáo khoa - Học tiếng Anh - Bài giảng trực tuyến - Món ăn bài thuốc - Chăm sóc bà bầu - Môi trường - Tiết kiệm điện - Nhi khoa - Ung thư - Tác hại của thuốc lá - Các kỹ thuật dạy học tích cực
- Dạy học phát triển năng lực - Chương trình giáo dục phổ thông
Tính diện tích hình tròn
Từ VLOS
Bài
toán
phổ
biến
trong
những
giờ
toán
hình
học
là
yêu
cầu
chúng
ta
tính
diện
tích
của
một
hình
tròn
dựa
trên
thông
tin
đã
biết.
Công
thức
tính
diện
tích
hình
tròn
là:
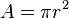 .
Công
thức
này
khá
đơn
giản,
bạn
chỉ
cần
biết
giá
trị
của
bán
kính
là
sẽ
tính
được
diện
tích
hình
tròn.
Tuy
nhiên,
bạn
cũng
cần
phải
luyện
tập
cách
chuyển
đổi
một
số
đơn
vị
dữ
liệu
đã
cho
thành
những
số
hạng
có
thể
áp
dụng
vào
công
thức
này.
.
Công
thức
này
khá
đơn
giản,
bạn
chỉ
cần
biết
giá
trị
của
bán
kính
là
sẽ
tính
được
diện
tích
hình
tròn.
Tuy
nhiên,
bạn
cũng
cần
phải
luyện
tập
cách
chuyển
đổi
một
số
đơn
vị
dữ
liệu
đã
cho
thành
những
số
hạng
có
thể
áp
dụng
vào
công
thức
này.
Mục lục
Các bước[sửa]
Dùng bán kính để tìm diện tích[sửa]
-
Xác
định
bán
kính
của
hình
tròn.
Bán
kính
là
độ
dài
từ
tâm
đến
cạnh
của
hình
tròn.
Dù
bạn
đo
theo
bất
cứ
hướng
nào,
bán
kính
vẫn
là
như
nhau.
Bán
kính
cũng
chính
là
một
nửa
đường
kính
hình
tròn.
Đường
kính
là
đoạn
thẳng
đi
qua
tâm
và
nối
hai
phía
đối
diện
của
hình
tròn
với
nhau.[1]
- Đề bài thường cho sẵn bán kính. Hơi khó để xác định chính xác tâm của hình tròn, trừ khi nó đã được cho sẵn trên hình vẽ đề bài cung cấp.
- Trong ví dụ này, giả sử đề bài cho bạn bán kính hình tròn là 6 cm.
-
Bình
phương
bán
kính.
Công
thức
tính
diện
tích
hình
tròn
là
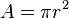 ,
trong
đó
biến
,
trong
đó
biến
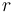 đại
diện
cho
bán
kính.
Biến
này
được
bình
phương
lên.[1]
đại
diện
cho
bán
kính.
Biến
này
được
bình
phương
lên.[1]
- Đừng nhầm lẫn và bình phương toàn bộ biểu thức.
-
Ví
dụ:
một
hình
tròn
có
bán
kính,
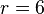 ,
ta
có
,
ta
có
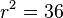 .
.
-
Nhân
với
pi.
Pi
là
một
hằng
số
toán
học
đại
diện
cho
tỉ
lệ
giữa
chu
vi
và
đường
kính
hình
tròn.
Nó
được
ký
hiệu
bằng
chữ
cái
Hy
lạp
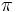 .[2]
Sau
khi
làm
tròn
theo
số
thập
phân,
.[2]
Sau
khi
làm
tròn
theo
số
thập
phân,
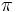 gần
bằng
3,14.
Giá
trị
số
thập
phân
đúng
thật
ra
còn
kéo
dài
vô
tận.
Thông
thường,
để
trình
bày
diện
tích
hình
tròn
một
cách
chính
xác,
chúng
ta
sẽ
viết
đáp
số
theo
ký
hiệu
gần
bằng
3,14.
Giá
trị
số
thập
phân
đúng
thật
ra
còn
kéo
dài
vô
tận.
Thông
thường,
để
trình
bày
diện
tích
hình
tròn
một
cách
chính
xác,
chúng
ta
sẽ
viết
đáp
số
theo
ký
hiệu
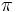 .[1]
.[1]
-
Với
ví
dụ
về
hình
tròn
có
bán
kính
là
6
cm,
diện
tích
sẽ
được
tính
như
sau:
-
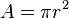
-
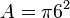
-
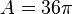 hay
hay
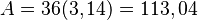
-
-
Với
ví
dụ
về
hình
tròn
có
bán
kính
là
6
cm,
diện
tích
sẽ
được
tính
như
sau:
-
Trình
bày
đáp
án.
Nhớ
rằng
khi
tính
toán
diện
tích,
đơn
vị
phải
luôn
được
trình
bày
kèm
theo
dấu
“bình
phương”
(đọc
là
vuông).
Nếu
bán
kính
được
tính
bằng
xăng-ti-mét,
diện
tích
sẽ
là
xăng-ti-mét
vuông.
Nếu
bán
kính
được
tính
theo
mét,
diện
tích
sẽ
là
mét
vuông.
Bạn
cũng
cần
biết
đề
yêu
cầu
chúng
ta
trình
bày
đáp
số
như
thế
nào:
theo
ký
hiệu
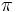 hay
tính
ra
số
thập
phân
làm
tròn?
Nếu
như
không
biết,
hãy
trình
bày
theo
cả
hai
cách.[1]
hay
tính
ra
số
thập
phân
làm
tròn?
Nếu
như
không
biết,
hãy
trình
bày
theo
cả
hai
cách.[1]
-
Đối
với
hình
tròn
có
bán
kính
6
cm,
diện
tích
sẽ
là
36
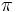 cm2
hay
113,04
cm2.
cm2
hay
113,04
cm2.
-
Đối
với
hình
tròn
có
bán
kính
6
cm,
diện
tích
sẽ
là
36
Tính diện tích theo đường kính[sửa]
-
Đo
hay
viết
lại
đường
kính.
Trong
một
số
bài
toán
hay
tình
huống,
bạn
sẽ
không
biết
được
bán
kính.
Thay
vào
đó,
bạn
sẽ
chỉ
biết
độ
dài
đường
kính
của
hình
tròn.
Nếu
đường
kính
được
vẽ
trong
sơ
đồ
bài
toán,
bạn
có
thể
dùng
thước
để
đo.
Hoặc,
bài
toán
sẽ
cho
sẵn
độ
dài
của
đường
kính.
- Giả sử, bạn có hình tròn với đường kính 20 cm.
-
Chia
đôi
đường
kính.
Nhớ
rằng
đường
kính
dài
gấp
đôi
bán
kính.
Vì
thế,
bất
kể
đề
bài
cho
bạn
giá
trị
đường
kính
là
bao
nhiêu,
chỉ
cần
chia
đôi
nó
ra
bạn
sẽ
có
được
bán
kính.
- Theo ví dụ trên, hình tròn với đường kính 20 cm sẽ có bán kính là 20/2 = 10 cm.
-
Áp
dụng
công
thức
dính
diện
tích
cơ
bản.
Sau
khi
chuyển
đổi
đường
kính
thành
bán
kính,
đây
là
lúc
bạn
sử
dụng
công
thức
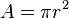 để
tính
diện
tích
hình
tròn.
Gán
giá
trị
của
bán
kính
vào
và
tiến
hành
phép
tính
còn
lại
như
sau:
để
tính
diện
tích
hình
tròn.
Gán
giá
trị
của
bán
kính
vào
và
tiến
hành
phép
tính
còn
lại
như
sau:
-
-
Trình
bày
giá
trị
của
diện
tích.
Xin
nhắc
lại,
đơn
vị
diện
tích
của
hình
tròn
sẽ
đi
cùng
với
dấu
“bình
phương”.
Trong
ví
dụ
này,
đường
kính
được
tính
bằng
cm,
vì
thế,
bán
kính
cũng
được
tính
bằng
cm.
Vậy,
diện
tích
sẽ
được
tính
theo
cm
vuông.
Đáp
số
ở
đây
sẽ
là
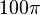 cm2.
cm2.
-
Bạn
cũng
có
thể
cung
cấp
một
số
thập
phân
bằng
cách
thay
3,14
cho
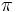 .
Kết
quả
của
biểu
thức
là
(100)(3,14)
=
314
cm2.
.
Kết
quả
của
biểu
thức
là
(100)(3,14)
=
314
cm2.
-
Bạn
cũng
có
thể
cung
cấp
một
số
thập
phân
bằng
cách
thay
3,14
cho
Dùng chu vi để tính diện tích[sửa]
-
Tìm
hiểu
về
công
thức
biến
đổi.
Nếu
biết
chu
vi
đường
tròn,
bạn
có
thể
dùng
công
thức
biến
đổi
để
tìm
diện
tích
hình
tròn
đó.
Công
thức
biến
đổi
này
gán
thẳng
giá
trị
chu
vi
để
tính
diện
tích,
bạn
không
cần
phải
tìm
bán
kính.
Công
thức
mới
là:
-
-
Đo
hoặc
viết
ra
chu
vi.
Trong
một
số
tình
huống
ngoài
thực
tế,
bạn
không
thể
đo
đường
kính
hay
bán
kính
một
cách
chính
xác.
Rất
khó
để
ước
lượng
tâm
của
hình
tròn
nếu
đường
kính
hay
tâm
của
hình
tròn
đó
không
được
định
sẵn.
Đối
với
một
số
vật
thể
có
hình
tròn
–
chẳng
hạn
như
một
chiếc
chảo
nướng
pizza
hay
chảo
rán
–
bạn
có
thể
dùng
thước
dây
để
đo
chu
vi,
chính
xác
hơn
nhiều
so
với
việc
đo
đường
kính.[3]
- Trong ví dụ này, giả sử bạn có hình tròn (hay một vật hình tròn) với chu vi là 42 cm.
-
Sử
dụng
mối
quan
hệ
giữa
chu
vi
và
bán
kính
để
biến
đổi
công
thức.
Chu
vi
của
một
đường
tròn
bằng
pi
nhân
với
đường
kính
hay
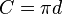 .
Tiếp
theo,
nhớ
lại
rằng
đường
kính
bằng
hai
lần
bán
kính,
hay
.
Tiếp
theo,
nhớ
lại
rằng
đường
kính
bằng
hai
lần
bán
kính,
hay
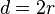 .
Bạn
có
thể
kết
hợp
hai
biểu
thức
này
để
tạo
ra
mối
quan
hệ
sau:
.
Bạn
có
thể
kết
hợp
hai
biểu
thức
này
để
tạo
ra
mối
quan
hệ
sau:
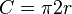 .
Sắp
xếp
lại
biểu
thức
nhằm
cô
lập
biến
r
.
Sắp
xếp
lại
biểu
thức
nhằm
cô
lập
biến
r
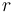 ,
ta
có:[3]
,
ta
có:[3]
-
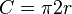
-
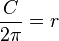 …..
(chia
hai
bên
cho
2
…..
(chia
hai
bên
cho
2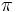 )
)
-
-
Thay
vào
công
thức
tính
diện
tích
hình
tròn.
Tận
dụng
mối
quan
hệ
giữa
chu
vi
và
bán
kính,
bạn
sẽ
tạo
ra
được
bản
sửa
đổi
của
công
thức
tính
diện
tích
hình
tròn.
Thay
biểu
thức
cuối
cùng
vào
công
thức
tính
diện
tích
ban
đầu,
ta
có:[3]
-
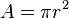 …..(công
thức
tính
diện
tích
ban
đầu)
…..(công
thức
tính
diện
tích
ban
đầu) -
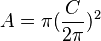 …..
(thay
biểu
thức
của
r
vào)
…..
(thay
biểu
thức
của
r
vào) -
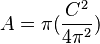 …..(bình
phương
phân
số)
…..(bình
phương
phân
số) -
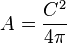 …..(đơn
giản
…..(đơn
giản
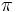 ở
tử
số
và
mẫu
số)
ở
tử
số
và
mẫu
số)
-
-
Áp
dụng
công
thức
biến
đổi
để
tính
diện
tích.
Áp
dụng
công
thức
biến
đổi
được
viết
lại
với
chu
vi
thay
vì
bán
kính
cùng
với
thông
tin
mà
bạn
có
để
tìm
diện
tích
chính
xác.
Gán
giá
trị
của
chu
vi
vào
và
tiến
hành
tính
toán
như
sau:[3]
-
Trong
ví
dụ
này,
bạn
có
chu
vi
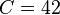 cm.
cm. -
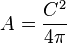
-
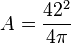 …..(thay
giá
trị
vào)
…..(thay
giá
trị
vào) -
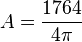 .….(tính
422)
.….(tính
422) -
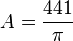 …..(chia
cho
4)
…..(chia
cho
4)
-
Trong
ví
dụ
này,
bạn
có
chu
vi
-
Đưa
ra
đáp
án.
Trừ
khi
chu
vi
mà
bạn
có
là
bội
số
của
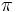 ,
nếu
không
thì
kết
quả
của
bạn
sẽ
là
một
phân
số
với
,
nếu
không
thì
kết
quả
của
bạn
sẽ
là
một
phân
số
với
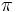 là
mẫu
số.
Đáp
án
này
không
sai.
Bạn
nên
trình
bày
đáp
số
tính
diện
tích
theo
kiểu
này,
hoặc
là
tính
đáp
số
xấp
xỉ
bằng
cách
thay
pi
bằng
3,14.[3]
là
mẫu
số.
Đáp
án
này
không
sai.
Bạn
nên
trình
bày
đáp
số
tính
diện
tích
theo
kiểu
này,
hoặc
là
tính
đáp
số
xấp
xỉ
bằng
cách
thay
pi
bằng
3,14.[3]
-
Trong
ví
dụ
này,
hình
tròn
với
chu
vi
42
cm
sẽ
có
diện
tích
là
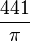 cm2
cm2 -
Nếu
muốn
tính
ra
số
thập
phân,
ta
có
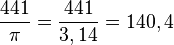 .
Diện
tích
gần
bằng
140
cm2.
.
Diện
tích
gần
bằng
140
cm2.
-
Trong
ví
dụ
này,
hình
tròn
với
chu
vi
42
cm
sẽ
có
diện
tích
là
Tính diện tích bằng hình quạt tròn[sửa]
-
Xác
định
thông
tin
đã
biết
hay
đã
cho.
Một
số
bài
toán
sẽ
cho
bạn
thông
tin
về
hình
quạt
tròn
của
hình
tròn
và
đề
bài
sẽ
yêu
cầu
bạn
tính
diện
tích
toàn
phần
của
hình
tròn
đó.
Đọc
kỹ
đề
bài
một
cách
cẩn
thận
và
tìm
xem
có
thông
tin
nào
tương
tự
như,
“Một
hình
quạt
tròn
của
hình
tròn
O
có
diện
tích
là
15
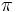 cm2.
Tính
diện
tích
của
hình
tròn
O.”[4]
cm2.
Tính
diện
tích
của
hình
tròn
O.”[4] - Xác định hình quạt tròn đã cho. Hình quạt tròn của hình tròn là một phần chia của hình tròn. Một hình quạt tròn được xác định bằng cách vẽ hai đường bán kính từ tâm đến cạnh của đường tròn. Khoảng trống giữa hai bán kính đó chính là hình quạt tròn.[4]
-
Tính
góc
ở
tâm
của
hình
quạt
tròn.
Dùng
thước
đo
góc
để
đo
góc
giữa
tạo
ra
bởi
hai
bán
kính.
Đặt
cạnh
đáy
của
thước
đo
góc
dọc
theo
một
đường
bán
kính,
trung
tâm
của
thước
trùng
với
tâm
hình
tròn.
Sau
đó
đọc
số
đo
góc
nằm
ở
vị
trí
của
bán
kính
thứ
hai
tạo
thành
hình
quạt
tròn.[4]
- Chắc rằng bạn đo đúng góc nhỏ giữa hai bán kính chứ không phải góc lớn hơn nằm phía ngoài. Thông thường, bài toán mà bạn đang giải sẽ cho bạn số liệu này. Tổng của góc nhỏ và góc lớn sẽ là 360 độ.
- Trong một số bài toán, đề bài sẽ cho bạn số đo góc. Ví dụ: “Góc ở tâm của hình quạt tròn là 45 độ”, nếu không có số liệu, bạn sẽ phải tiến hành đo.
-
Áp
dụng
công
thức
biến
đổi
để
tính
diện
tích.
Khi
bạn
biết
diện
tích
của
hình
quạt
tròn
và
số
đo
góc
ở
tâm
của
nó,
bạn
có
thể
áp
dụng
công
thức
biến
đổi
để
tìm
diện
tích
của
hình
tròn:[4]
-
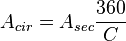
-
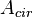 là
diện
tích
toàn
phần
của
hình
tròn
là
diện
tích
toàn
phần
của
hình
tròn -
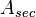 là
diện
tích
của
hình
quạt
tròn
là
diện
tích
của
hình
quạt
tròn -
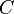 là
số
đo
góc
ở
tâm
là
số
đo
góc
ở
tâm
-
-
-
Nhập
các
giá
trị
mà
bạn
biết
và
tính
diện
tích.
Trong
ví
dụ
này,
bạn
đã
có
góc
ở
tâm
là
45
độ
và
hình
quạt
tròn
có
diện
tích
là
15
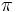 .
Thay
những
số
liệu
này
vào
công
thức
và
tiến
hành
như
sau:[4]
.
Thay
những
số
liệu
này
vào
công
thức
và
tiến
hành
như
sau:[4]
-
-
Đưa
ra
đáp
án.
Trong
ví
dụ
này,
hình
quạt
tròn
bằng
1/8
diện
tích
toàn
phần
của
hình
tròn.
Vậy,
diện
tích
toàn
phần
của
hình
tròn
là
120
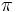 cm2.
Diện
tích
hình
quạt
tròn
ban
đầu
được
cho
theo
cm2.
Diện
tích
hình
quạt
tròn
ban
đầu
được
cho
theo
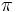 ,
vì
thế,
bạn
nên
trình
bày
diện
tích
của
toàn
bộ
hình
tròn
theo
cách
tương
tự.[4]
,
vì
thế,
bạn
nên
trình
bày
diện
tích
của
toàn
bộ
hình
tròn
theo
cách
tương
tự.[4]
- Nếu bạn muốn trình bày đáp án theo dạng số, thực hiện phép tính 120 x 3,14, kết quả là 376,8 cm2.