Hàm số liên tục (một cách hiểu)
Liên tục có nghĩa là không bị gián đoạn. Định nghĩa một cách trực giác, hàm số liên tục khi và chỉ khi nó có đồ thị được vẽ bằng 1 nét liền mạch.
Không có gì ấn tượng hơn việc so sánh đồ thị của 1 hàm số liên tục với đường nhớt mà con ốc sên bỏ lại khi nó bò trên 1 cái sân láng xi măng. Ai cũng biết ốc sên không biết nhảy, vì thế nó chỉ có thể bò một cách từ từ, liên tục và nhẫn nại. Vệt nhớt mà nó bỏ lại chính vì thế trở nên một nét đậm óng ánh và liền mạch.
Bây giờ nếu cái sân đó bị một cách vạch vôi ngăn làm đôi. Ốc sên muốn bò từ nửa sân bên này sang nửa bên kia, thì chắc chắn nó phải bò qua cái vạch vôi này. Vì thế mà vệt nhớt của nó cắt ngang đường vạch vôi.
Từ sự so sánh ngộ nghĩnh đó, ta có thể liên tưởng đến tính chất kì diệu sau của hàm số:
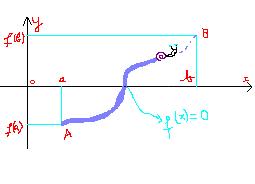
Nếu f(x) liên tục trên đoạn [a,b], f(a) và f(b) trái dấu nhau. Như thế thì phương trình f(x) = 0 sẽ có nghiệm trên đoạn [a,b]”.
Để khảo sát vấn đề này, trước hết, ta hãy xét trường hợp f(a)<0 và f(b)>0 (trường hợp f(a)>0 và f(b)<0 hoàn toàn tương tự).
Bạn hãy tưởng tượng trang vở mà bạn vẽ đồ thị f(x) là 1 cái sân xi măng, trục Ox là cái vạch vôi chia đôi cái sân xi măng này. Ta lấy 2 điểm: A=(a,f(a)) và B=(b,f(b)).
Ban đầu “ốc sên” xuất phát từ điểm A, nó muốn bò đến điểm B, và để lại 1 vệt nhớt trùng với đồ thị của f(x). Điểm A nằm dưới vạch vôi, mà điểm B lại ở phía trên. Chú “ốc sên” muốn đến B thì bắt buộc phải băng qua cái vạch vôi, nghĩa là đồ thị của f(x) phải cắt Ox tại một điểm nào đó nằm giữa a và b. Cái điểm này có hoành độ là nghiệm của f(x) = 0. Suy ra đpcm.