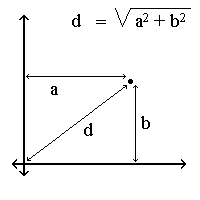Hình học bội phân (Fractals)

Em dang lam mot cai projet ve van de nay nhung qua that vi no qua lon nen em cung khong ro het nhung ung dung cu the! Em moi chi biet mot so ung dung nhu chaos trong he mat troi, problème 3 corps cua Poincaré hay cac ly thuyet cua Laurent Nottale, doc cac tai lieu tren mang thi that su la rat rat nhieu . Vay co bac nao hieu biet sau rong ve linh vuc nay thi xin giang giai cho em voi de mo rong them dau oc.

Em cũng có các vấn đề tương tự như là:

• Các phương trình fractal được tạo ra như thế nào?
• Lam sao để biểu diễn các fractal này bằng ngôn ngữ lập trình?
• Nguyên lý hay nguyên tắc chính cua fractal?

Kính xin các thầy cô giáo sư trong vietsciences vui lòng chỉ điểm

Thành Luân

ĐHSP Hà Nội, Khoa Tin Học

Hình học bội phân (Fractals)

Vào Google, key in : fractal dimension, các bạn có thể vào rất nhiều website nói về hình thể học bội phân, nhưng rất khó hiểu. Đây là vài nơi giải thích về Fractal:

• http://www.gisdevelopment.net/aars/acrs/1997/ts9/ts9005a.shtml
• http://www.vanderbilt.edu/AnS/psychology/cogsci/chaos/workshop/2DS.html
• http://www.people.umass.edu/mray/physics/fractals.html
• http://www.jracademy.com/~jtucek/math/dimen.html

Khó hiểu không phải tại chúng ta kém thông minh hay tại đề tài này quá cao siêu đối với trình độ chúng ta, mà khó hiểu vì Mỹ không biết cách giảng giải kiểu Việt Nam. Sau vài ngày viết bài và thử nghiệm cách giảng giải của Meta tự chế với 1 máy calculator, Meta viết lại Hình thể học bội phân (fractal và mandelbrot) sao cho bất cứ ai cũng hiểu, kể cả người thiếu trình độ. (Xin lỗi, Meta không có ý kiêu ngạo) Xin đọc. Bảo đảm hiểu ngay .

---

Bờ biển Việt Nam dài bao nhiêu? Thiên thượng phù vân như bạch y, phiêu du hốt biến vi thương cẩu. Những đám mây trên trời có hình dạng gì? Lá phổi con người có giống với những cửa sông và một nhánh cải súp lơ? Câu trả lời là Fractals, mà Meta xin phép dịch thoát nghĩa là Hình Học Siêu Kích Thước. Sẽ cắt nghĩa nguyên ủy cụm từ này. Những hình thể siêu kích thước là những hình dạng chẳng nằm trong kích thước nào cả và đóng vai trò phát sinh ra những nguyên lý về sự hỗn loạn (principles of chaos).

Từ thời cổ Hy Lạp, các khoa học gia đã hình dung thế giới trong khuôn khổ các hình thể chuẩn và đơn giản – hình tròn, tam giác, khối lập phương, hình chóp và khối cầu v.v…Theo hình học này, một điểm không có kích thước; một đường thẳng gồm 1 kích thước; một mặt phẳng có 2 kích thước và một thể tích có 3 kích thước. Nhưng làm thế nào một hình tròn hay tam giác có thể miêu tả được dạng thức của băng giá đóng ngoài kính cửa sổ, vết nứt của mặt đường lộ hay cái gập ghềnh của con đường đèo bên sườn núi? Nhà toán học Mandelbrot nhận thấy cần phải phát minh ra một toán học hoàn toàn mới có khả năng mô tả những hình dạng bất quy tắc.

Chiều dài bờ biển Việt Nam chính xác là bao nhiêu? Mandelbrot khám phá ra đáp án rằng nó tùy thuộc vào bạn đo nó như thế nào. Thoạt tiên bạn cần 1 tấm bản đồ và một cuộn dây (cuộn chỉ cũng được), khéo léo uốn sợi dây ấy lần theo bờ biển trên bản đồ, xong xuôi đo sợi chỉ rồi nhân cho tỷ lệ xích (scale).

Nhưng giả sử bạn dùng một bản đồ với tỷ lệ xích lớn. Các chi tiết về cửa sông, doi đất khiến sợi chỉ dùng để đo sẽ dài hơn lần đo ban đầu rất nhiều. Nếu bạn dùng thước vừa đi vừa đo suốt từ ải nam Quan cho chí mũi Cà Mau, đáp số còn dài hơn nữa. Nhưng đó có phải là chiều dài chính xác của bờ biển nước ta hay không? Thưa không. Bởi vì cây thước đo của bạn sẽ bỏ sót những khúc quanh co, uốn éo nhỏ hơn chiều dài cây thước.

Thế thì chiều dài thực sự của bờ biển Việt Nam là bao nhiêu? Mandelbrot giải thích, bờ biển dài vô tận bởi vì cái hình thể phức tạp vô tận của nó. Đấy là chỉ nói về hình dạng, Meta chưa nói đến những … nguyên tử hạt cát viền theo bờ biển. Nếu thế thì chẳng có cách nào biết được bề dài bờ biển nước ta hay sao? Mandelbrot nói: Không hẳn thế. Điều quan trọng không phải là chiều dài mà là hình thể có thể được đo một cách rõ rệt hay không.

Mandelbrot gọi đường nét cực kỳ phức tạp đó là hình thể siêu kích thước (Fractals). Mỗi một đường nét cực phức này có 1 kích thước có thể dung chứa một sự đo đạc chính xác về cái phức tạp nội tại của nó.

Mandelbrot cho biết rằng cái đường viền quanh ngọn núi cũng thế. Cái gập ghềnh khúc khuỷu của nó không ngừng thay đổi khi bạn bước trên núi và tùy thuộc cách bạn đo đạc. Mặt khác, hình thể cực phức của nó nổi bật một cách rõ rệt so với nền trời. Có rất nhiều hình thể phức tạp như thế trong thiên nhiên như mây, các cửa sông, lá phổi, cải súp lơ, biến chuyển thời tiết, vết nứt xi măng, tiếng ồn máy radio (noise), bụi không gian, các luồng gió thốc, nhánh cây đòi hỏi vận dụng Hình Học Siêu Kích Thước để mô tả thay vào dùng những hình tròn, tam giác, hình chóp cổ điển.

Làm thế nào vật thể có được Siêu Kích Thước nằm giữa mặt phẳng và hình khối hay giữa 1 điểm và 1 đường thẳng? Câu trả lời chuẩn xác là toán học nhưng để Meta cắt nghĩa bằng dẫn giải cho dễ hiểu. Bạn có biết một nùi dây cuốn lại thành khối cầu không? Nhìn từ tuốt ngoài xa, nó nhỏ xíu như 1 điểm (1 điểm được hình học cổ điển định nghĩa là không có kích thước). Khi đến gần ta thấy nó là một khối cầu. Rõ ràng hơn, ta thấy nó là một nùi dây cuộn lại thành hình cầu (tức là 3 chiều). Nùi dây ấy nếu gỡ ra thành một đường thẳng thì chỉ có 1 kích thước. Nhìn kỹ hơn ta thấy sợi dây thành một khối hình trụ dài (lại là 3 chiều). Nhìn bằng kính lúp, hình trụ này do những sợi tơ nhỏ bện lại. Vậy cuộn dây này có bao nhiêu kích thước? Cho phép Meta gọi là siêu kích thước nhé bởi chúng ta sắp sửa đi sâu vào toán Fractals, Hình Học Siêu Kích Thước.

Thử hình dung nữa về siêu kích thước. Rải 10000 hạt gạo lên trên một bàn cờ tướng. Đừng để cho gà qué mổ hay bố vợ đổ đi. Chú ý vào 1 đường kẻ trên bàn cờ. Giả thử bạn quởn tới mức đếm những hạt gạo trên đường kẻ đó. Được 200 hạt. Hãy ví dụ thế. Bây giờ lấy bút vẽ 1 đường ngoằn ngoèo sao cho đường vẽ ấy đi qua càng nhiều hạt gạo càng tốt. Đường vẽ càng lúc càng phức tạp, nghĩa là càng quanh co uốn éo. Cuối cùng, đường phức tạp này đi qua tất cả hạt gạo trên bàn cờ. Đường kẻ này có còn là 1 kích thước nữa không? Giả dụ hạt gạo là 1 điểm nhỏ xíu không kích thước, 1 đường ngoằn ngoèo đi qua mọi điểm không kích thước ấy sẽ trở thành diện tích gồm chiều dài và rộng (tức là 2 chiều). Đường vẽ giả định này có thực, ít nhất theo lý thuyết. Nó được gọi là đường cong Peano (Nếu muốn biết về lão Peano thì Meta viết sau. Bây giờ tập trung vào Fractals đã.) Rõ ràng đường cong biến thành mặt phẳng. Lúc này bà vợ ngu tối của bạn phán một câu chí lý:

- Sao anh không lấy cái cọ sơn cái bàn cớ tướng có phải nhanh hơn không?

Phải đấy, dùng cái bút vẽ một đường đi qua mọi điểm khác nào tô mực lên mặt phẳng. Ta không vẽ 1 đường cong ngoằn ngoèo nữa mà là tô mực kín bàn cờ tướng. Đường cong phức tạp ấy biến thành mặt phẳng 2 chiều.

Cũng chẳng lạ lắm đâu. Chúng ta hẳn không lạ gì lão Riemann, nhà toán học người Đức sinh năm 1826 ở Hanover. Hình học cổ điển cho rằng hình chữ nhật giống như tờ giấy phẳng phiu – thơ tình chẳng hạn – ngoan ngoãn ép trong cuốn vở học trò, thơm ngát hương hoa quyện vào mùi mực. Nhưng lão này cho rằng trong thiên nhiên không có loại hình chữ nhật lý tưởng đến thế. Hình chữ nhật phải là 1 tờ giấy vo viên rồi vuốt thẳng. Những nhàu nát trên mặt tờ giấy chính là trọng lực. Giả dụ có 1 con sâu bò trên tờ giấy đó, nó sẽ bị “lôi” hoặc “kéo” vào những chỗ nhàu nát. Ấy là trọng lực. Lão Einstein sau này cũng cho rằng những chỗ trũng trong không gian do thiên thể hằn lên, chính là trọng lực. Kệ 2 lão ấy. Meta chỉ muốn hỏi rằng, tờ giấy nhàu nát ấy có 2 chiều hay mấy chiều? Nếu một hình thể 2 chiều choán chỗ trong không gian 3 chiều thì Meta gọi đó là siêu kích thước. Bằng lòng như vậy, nếu ủng oẳng cãi thì chẳng biết bao giờ mới sang phần lập trình.

Hehehe Meta hay lòng vòng chuyện nọ sọ sang chuyện kia. Lắm lúc đế biết mình nói gì. Như thế những đường cong nằm ở giữa 1 và 2 kích thước có thể vẽ được. Cũng lập luận như thế, cũng có những mặt phẳng (nhưng lồi lõm) nằm ở giữa 2 và 3 kích thước như tờ giấy của lão Riemann. Một tập hợp những hạt bụi không kích thước phức tạp cũng có kích thước giữa zero và 1. Trong mỗi trường hợp, siêu kích thước là cách duy nhất phân loại 1 hình dạng thiên nhiên và để đối chiếu nó với hình dạng khác.

Hình Học Siêu Kích Thước có đặc tính đáng chú ý. Chúng cực kỳ phức tạp, trên ý nghĩa rằng bất kỳ một chi tiết riêng biệt nào cũng có thể phóng đại để tiết lộ thêm những chi tiết nữa và cứ phóng đại như thế, nó phô bày thêm chi tiết như thế cho đến vô tận. Trong nhiều trường hợp chúng thừa hưởng những nét giống nhau, một hình dạng nào đó lập đi lập lại nếu chúng ta càng phóng đại thêm. Mandelbrot gọi 1 Hình Dạng Siêu Kích Thước đặc thù ông khám phá – Bộ Mandelbrot – là hình thể phức tạp nhất trong vũ trụ.

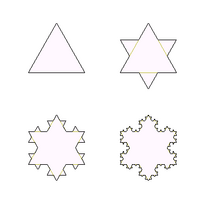
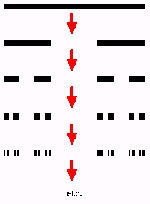
Hình Học Siêu Kích Thước được phát sinh bằng một tiến trình lập đi lập lại và có thể biểu thị trên máy vi tính cá nhân dùng một giải trình (algorithm) đơn giản. Lấy 1 ví dụ. Vẽ 1 tam giác và thay mỗi cạnh của nó với 1 hình tam giác đơn giản.

Kết quả là 1 ngôi sao. Thay mỗi cánh ngôi sao với 1 tam giác nhỏ nữa và cứ làm như thế ta sẽ có cái hình dạng như trên. Cuối cùng nó giống như 1 tinh thể tuyết. Lập lại giải trình (algorithm) đó và tiếp tục vô hạn. Dĩ nhiên trong lãnh vực vẽ vi tính, tiến trình này sẽ tiếp tục cho đến vô tận, nhưng ít nhất bạn có thể phóng đại bất cứ một phần nhỏ của hình thể ấy và phóng đại các chi tiết của nó mãi mãi. Hình dạng cuối cùng của nó có cực điểm chi tiết trong 1 siêu kích thước. Vì cách cấu tạo của nó, nó cũng tự đồng dạng (self-similarity), hình thể của nó lập đi lập lại trên quy mô càng nhỏ đi cho đến vô tận.

Trong sinh học, hãy xem xét vấn đề mang máu châu lưu khắp cơ thể. Máu là nhựa sống các sinh vật nhưng trên quan điểm sinh hóa (metabolism), nó là một thứ hàng hóa hiếm quý chỉ chiếm có 3/100 thể tích thân thể. Làm sao thiên nhiên trù hoạch 1 hệ thống tuần hoàn bảo đảm cho máu đến từng tế bào và cơ quan trong thân thể? Đáp án là sự phân nhánh siêu kích thước, trong đó các huyết quản chính tách ra giữa 8 và 30 lần trước khi đến các phần cá biệt trong cơ thể. Hình dạng cực phức của hệ tuần hoàn gần bằng 3 kích thước.

Phổi là một vấn đề thiết kế khác. Làm thế nào để máu tiếp xúc với không khí bên trong phổi. Trong trường hợp này, sự phân nhánh các ống dẫn khí diễn ra 10 lần và đột ngột đổi kiểu phân nhánh khác. Phổi có 1 cấu trúc phức tạp hơn hệ tuần hoàn. Nó không hẳn tự đồng dạng (self-similarity) vì giải trình (algorithm) phân nhánh thay đổi ở một quy mô nào đó.

Bộ não cũng có cấu trúc với kích thước khoảng 2.79 và 2.73. Ngay cả nhịp tim cũng có dạng cực phức. . Khi cái trật tự cực phức của nó đổi thành nhịp đều đặn, nó báo hiệu một cơn đau tim cận kề. Mặt khác, nếu hình thể siêu kích thước trở nên hỗn loạn, sự ngưng tập máu xảy ra. Ranh giới giữa sự phức tạp lành mạnh và hỗn loạn cũng thấy ở trong hoạt động của não.

Hình Học Siêu Kích Thước cũng được dùng mô tả hệ thống kinh tế và xã hội. Thị trường hối đoái là một hệ thống phi liên tục phức tạp (complicated nonlinear system) của những phản hồi cộng, trừ và tự chỉnh đốn (positive and negative feedbacks and self-corrections). Nó biểu thị mọi đặc điểm của phi liên tục – thời kỳ ổn định, xung động dội ngược (oscillations, chuyển động 1,2,3,4,3,2,1 … khác với chuyển động chu kỳ 1,2,3,4,1,2,3,4…), đột tăng và đột ngột sụp đổ. Một số nhà kinh tế ghi nhận sự trồi sụt thị trường hối đoái mang vẻ tự đồng dạng (self-similarity) của cực phức. Sự trồi sụt trong các khảo sát có vẻ ngẫu nhiên nhưng tiết lộ những khuôn mẫu lập đi lập lại ở khảng cách nhiều năm, nhiều tuần, nhiều ngày và ngay cả vài giờ. Điều có vẻ hỗn loạn vô trật tự trong sự trồi sụt hối đoái có lẽ là chứng cớ của sự hỗn loạn tiền định, trong đó sự trồi sụt chỉ xảy ra trong khoảng xác suất nào đó. Một số chuyên gia hối đoái dùng toán Hình Học Siêu Kích Thước (Fractals) để mua bán trong vòng vài giờ, và cũng để khai thác sự khác biệt tinh tế giữa trồi sụt tiền định và ngẫu nhiên thuần túy. (Nếu yêu cầu, trong tương lai Meta viết về Hỗn Loạn và Tự Chỉnh Đốn (Chaos and Self-Organization). Hình Học Siêu Kích Thước được tạo bởi sự lập đi lập lại hay giải trình (algorithm), nơi đáp số của 1 giai đoạn được dùng để tính đáp số kế tiếp. Sự tính toán liên hoàn này cũng có thể là nguyên nhân của hỗn loạn tiền định. Có lẽ phải có một lúc nào đó chúng ta nói về chuyện này.

Những phép toán cần biết để tính Fractals:

Số ảo

May mắn. Mandelbrot set chỉ cần 2 phép tính đơn giản. Đó là cách nhân số phức và cách tính đường huyền của 1 tam giác vuông góc dùng định lý Pythagore.

Trước tiên muốn biết cách nhân số phức, ta cần biết qua về số ảo cái đã. Trong cõi đời ô trọc này, thỉnh thoảng ta lại gặp căn số của 1 số âm. Đế biết con số ấy từ đâu mà ra. Có lẽ thấy 1 con số âm dễ rút căn quá, ví dụ con số -9, thấy ngon ăn, ta rút căn chơi cho vợ con lé con mắt. Thế nhưng, 1 con số dương hay 1 con số âm khi bình phương luôn cho ra dấu cộng. Nếu bình phương ra dấu cộng thì khi rút căn làm sao kết quả thành dấu âm được?

Toán học tạo ra một con số đặc biệt gọi là “i” mang trị số căn của -1. Do đó i^2 = -1. Để tính căn của 1 số âm ví dụ như -16, ta rút căn trị số tuyệt đối của số đó, trường hợp căn trị số tuyệt đối của -16 = 4 rồi nhân với “i”. Vậy căn -16 = 4i.

Để kiểm lại cho chắc, chúng ta bình phương 4i: 4 * 4 = 16 và i * i = -1, cho ra con số -16. Tóm lại, tất cả căn số của 1 số âm được gọi là số ảo . I viết tắt của chữ imaginary number.

Số phức

Khi 1 số trong dạng a + bi (1 số thực kèm theo 1 số ảo) thì được gọi là số phức. Trở lại vấn đề nêu trong phần số ảo: Trong cõi đời ô trọc này, thỉnh thoảng ta lại gặp căn số của 1 số âm. Đế biết con số ấy từ đâu mà ra? Con số ấy thường xuất hiện dù ta không muốn. Ví dụ trong phương trình bậc hai sau đây :

X2 -6x + 25 = 0ta có 2 căn số là 3 + 4i và 3 -4i. Làm sao biết chắc chúng là căn của đẳng thức? Để kiểm nghiệm lại, ta phục hồi đẳng thức trên bằng cách khai triển : (X - 3 -4i) * (X - 3 + 4i) = X^2 -3x +4Xi -3X +9 -12i -4Xi +12i -(4i)^2

Ta có thể bỏ +4Xi và -4Xi ở dòng trên cho gọn: X2 -3x -3X +9 -(16)*i^2

Vì i^2= -1 nên -(16)*i2 thành -(-16) = 16 và vì thế: X2 -6X +25 =0

Nhân số phức

Cộng và trừ số phức cũng giống như số học cơ bản, mà đề tài Fractal cũng đế cần cộng và trừ nên xin bỏ qua. Chỉ nên ôn lại toán nhân số phức. Nó chỉ hơi rắc rối 1 chút xíu:

(5 + 6i) * (7 + 8i)

Khai triển ra: 35 + 40i + 42i + 48i^2 Ta đã biết, i^2 = -1 cho nên 48i^2 = -48 Đáp số là = -13 + 82i

Dùng số phức để vẽ hình Fractal

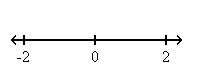
Đây là trục hoành có tâm là zero, có khoảng cách là số thực từ -2 đến 2.

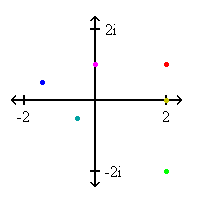
Còn trên đây là trục tung, có khoảng cách là số ảo từ -2i đến 2i. Vì số phức có 2 phần ảo và thực, chúng ta cần kích thước thứ 2 là trục tung để vẽ. Vì đồ thị có 2 kích thước, nó là một mặt phẳng, gọi là mặt số phức. Chúng ta vẽ bất cứ số phức nào trên mặt phẳng này. Những chấm màu tương ứng với số phức màu dưới đây: [2 + 1i], [-1.5 + 0.5i], [2 - 2i], [-0.5 - 0.5i], [0 + 1i], and [2 + 0i]

Cách tính những điểm cực phức

Chuỗi số Mandelbrot là một chuỗi số phức, chúng ta cứ theo đó mà chấm tọa độ trên mặt phẳng phức biểu hiện bằng trục thực ảo ở trên. Chúng ta cần tìm tầm xa (magnitude) để xem mỗi con số ở trong hay ngoài tầm. Chúng ta có công thức : Zn = (Zn-1)^2 + C. C là một hằng số phức, không thay đổi. Chỉ Z thay đổi sau mỗi lần lập lại công thức. Z bắt đầu bằng zero, nhưng thay đổi sau mỗi lần lập lại công thức. Có Z gồm 2 số thực và ảo, ta có thể chấm được 1 phát. Tài heng! Các bạn đế hiểu ngay bây giờ đâu nhưng đừng nóng, chút nữa có ví dụ cụ thể bằng số thì hiểu ngay.

Thực ra chúng ta không quan tâm đến trị số Z khi nó thay đổi mà chỉ nhìn vào cái tầm xa của nó để xác định nó ở trong hay ngoài tầm. Ví dụ, con số -9 là khoảng cách 9 từ zero, vậy tầm xa của nó là 9. Ấy là tầm xa của số thiên nhiên, chỉ để ví dụ thôi. Tầm xa của số phức thì khó tính hơn. Để tính tầm xa của số phức ta cộng bình phương khoảng cách trục tung và bình phương khoảng cách trục hoành và rút căn tổng số của nó. Công thức d=square root(a^2+b^2) luôn mất đi số ảo. Nếu d mang dấu âm thì bỏ dấu vì ta chỉ cần biết trị số tuyệt đối của nó, cách điểm ban đầu bao xa. Xin nhớ kỹ điều này.

Trong hình này, a là khoảng cách trục tung (số ảo) và b là khoảng cách trục hoành (số thực) và d là tầm xa. D chính là con số giúp ta quyết định điểm đó nằm trong hay ngoài hình cực phức.

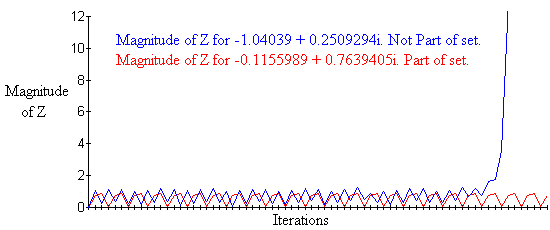
Khi chúng ta lập lại công thức (Zn = Zn-1)^2 + C. Z thay đổi và tầm xa của Z cũng thay đổi. Tầm xa của Z sẽ làm 1 trong 2 việc: Nó bằng hoặc nhỏ hơn 2. Bằng ngược lại nó sẽ vượt qua con số 2. Một khi nó vượt qua con số 2, nó sẽ tăng mãi mãi. Trường hợp nhỏ hơn hoặc bằng 2, Z là 1 phần của hình Mandelbrot. Nếu nó lớn hơn 2, nó nằm ngoài hình Mandelbrot.

Đường biểu diễn màu xanh sau vài chục lần lập đi lập lại công thức, nó tăng tiến đến vô cực. Tới đó, nó không còn thuộc về hình thể cực phức Mandelbrot nữa. Đừng nóng. Chỉ một chút nữa thôi khi sang qua phần ví dụ cụ thể thì các bạn hiểu ngay.

Lập trình mẫu về Mandelbrot set

Đây là lập trình mẫu về hình thể Mandelbrot set viết bằng C, không dùng recursive mà dùng loop. Nếu bạn có C compiler, run thử xem.

#include "stdio.h"
 
#define MaxIters 200
#define SIZE     80
#define BLACK    -1
#define LEFT     -2.0
#define RIGHT    1.0
#define TOP      1.0
#define BOTTOM   -1.0
 
main(int argc, char *argv[])
{
    short   x, y, count;
    long double zr, zi, cr, ci;
    long double rsquared, isquared;
 
    for (y = 0; y < SIZE; y++)
    {
        for (x = 0; x < SIZE; x++)
        {
            zr = 0.0;
            zi = 0.0;
            cr = LEFT + x * (RIGHT - LEFT) / SIZE;
 
            ci = TOP + y * (BOTTOM - TOP) / SIZE;
            rsquared = zr * zr;
            isquared = zi * zi;
 
            for (count = 0; rsquared + isquared <= 4.0
                            && count < MaxIters; count++)
            {
                zi = zr * zi * 2;
                zi += ci;
 
                zr = rsquared - isquared;
                zr += cr;
 
                rsquared = zr * zr;
                isquared = zi * zi;
            }
 
            if (rsquared + isquared <= 4.0)
                printf("*");
            else
                printf(" ");
        }
        printf("\n");
    }
    return 0;
}

Nếu bạn không rành lập trình thì Meta trích đoạn phần làm toán gồm 11 dòng:

for (count = 0; rsquared + isquared <= 4.0
                && count < MaxIters; count++)
{
    zi = zr * zi * 2;
    zi += ci;
 
    zr = rsquared - isquared;
    zr += cr;
 
    rsquared = zr * zr;
    isquared = zi * zi;
}

Thí dụ cụ thể:

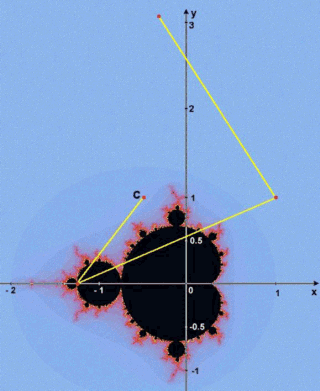
Hãy ôn lại công thức Zn = (Zn-1)^2 + C và tầm xa (Distance from the origin) = square root (a^2 + b^2). Chọn hằng số phức C = -0.5 + i. (Nghĩa là chấm đầu tiên trục hoành = -0.5 và trục tung= 1).

Lập lại công thức Zn = (Zn-1)^2 + C sẽ cho ra những trị số phức sau:

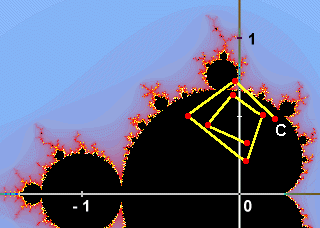
Step # …………	Current_Value …………	Distance from the origin
1 ……………….	-0.5 + i …………………. 	1.12
2 ……………….	-1.25 …………………….	1.25
3 ……………….	1.06 + i …………………. 1.46
4 ……………….	-0.37 + i * 3.1 …………..	3.12
 
Step 1: theo công thức tầm xa (Distance from the origin)= square root(-.5^2 + i^2). Vì i^2= -1, như trên trong đoạn nói về tầm xa, Meta đã nói ta chỉ cần trị số tuyệt đối của trục tung, nên dấu trừ bỏ đi. Ta có tầm xa = square root (.25+1) = 1.12.
Step 2: Để tính Z, ta có công thức : Zn = (Zn-1)^2 + C. Tức là Z step2 = (Z step 1)^2 + i. Z step1 chính là -.5 + i.
Thay số vào ta có : (-.5+i) * (-.5+i) => .25 - .5i - .5i +i^2. Thay i^2 = -1 và thu gọn lại, ta có :
Z step2 = .25 – 1i -1 => - .75-i
Z step2 = - .75 – i + C = - .75 - .5 –i +i
Z step2 = -1.25
Lúc này tầm xa = square root (-1.25)^2  thì vẫn bằng 1.25. Nhắc lại, tầm xa luôn bỏ dấu.
Step3: Cũng lập lại công thức Zn = (Zn-1)^2 + C. Ta có Z step3 = (Z step2)^2 + C.
Thay số:
Z step3 = -1.25^2 + C. C là hằng số phức, bao giờ cũng bằng -.5 + i.
Z step3 =1.56 + -.5 + i => 1.06 + i.
Tầm xa = square root (1.06^2 + i^2). Vì i^2 = -1 nhưng tầm xa bỏ dấu nên:
Tầm xa = square root (1.12 + 1) = 1.46
Step 4: Z step4 = (Z step3)^2 + C => (1.06 +i) * (1.06 +i) + C
Z step4 = 1.06 * 1.06 + 1.06i + 1.06i + i^2 => 1.12 + 2.12i -1 + C
Z step4 = .12 + 2.12i + -0.5 + i
Z step4 = -.37 + 3.1i
Tầm xa = square root (-.37^2 + 3.1i^2)  =>.13 + 9.61 * 1 = 3.12
Tầm xa này vượt ra ngoài hình thể Maldelbrot. Nếu lập lại nữa, sẽ tiến đến vô cực.
 
Bây giờ chúng ta chọn hằng số phức C = 0.2 + i * 0.5 nhé. Trường hợp này khoảng cách từ khởi điểm không bao giờ vượt quá 2. khi chúng ta đạt được tối đa số lần lập lại (ví dụ là 200) chúng ta cho rằng khởi điểm C thuộc về hình thể Mandelbrot và chúng ta tô màu đen.

Step # …………	Current_Value …………	Distance from the origin
1 ……………….	0.2 + i * 0.5 ……………..	0.54
2 ……………….	-0.01 + i * 0.7 …………..	0.7
3 ……………….	-0.29 + i * 0.49 …………	0.57
4 ……………….	0.05 + i * 0.22 …………. 	0.22
5 ……………….	0.15 + i * 0.52 …………. 	0.54
6 ……………….	-0.05 + i * 0.66 …………	0.66
7 ……………….	-0.23 + i * 0.44 …………	0.48
8 ……………….	0.06 + i * 0.3 ……………	0.3
. .	. . . . . . . . . . . . 	. . . .
 
Step 1: theo công thức tầm xa (Distance from the origin)= square root(-.2^2 + 0.5i^2). Vì i^2= -1, như trên trong đoạn nói về tầm xa, Meta đã nói ta chỉ cần trị số tuyệt đối của trục tung, nên dấu trừ bỏ đi. Ta có tầm xa = square root (.04+.25*1)
Tầm xa = 0.54.
Step 2: Để tính Z, ta có công thức : Zn = (Zn-1)^2 + C. Tức là Z step2 = Z step1^2 + i.
Z step1 chính là 0.2 +.5i.
Thay số vào ta có : (.2 +.5i) * (.2 +.5i) +C => .04 + .1i + .1i +.25i^2 +C . Thay i^2 = -1 và thu gọn lại:
Z step2 =  .04 -.25 + .2i +C => - .21 +.2i +C
Z step2 = - .21 +.2i + .2 +.5i
Z step2 = -.01 + .7i
Tầm xa = square root (-.01^2 + .7i^2 ) = (.00+.7)^2
Tầm xa =  .7.
Nhắc lại, tầm xa i^2 luôn luôn bỏ dấu. i^2 = 1 chứ không phải -1.
Step3: Cũng lập lại công thức Zn = (Zn-1)^2 + C. Ta có Z step3 = (Z step2)^2 + C.
Thay số:
Z step3 = (-0.01 + 0.7i)^2 + C. C là hằng số phức, bao giờ cũng bằng 0.2 + 0.5i.
Z step3 =(-0.01 + 0.7i) * (-0.01 + 0.7i ) + C => (.00 +.007i + .007i + .49 * -1) +C
Z step3 = .014i -.49 + C => .014i - .49 + 0.2 + 0.5i
Z step3 = -.29 + .49i
Tầm xa = square root (.29^2 + .49i^2). i^2 = -1 nhưng tầm xa bỏ dấu nên:
Tầm xa = square root (.08 + .24 *1) = 0.57
 
Step4: …………………………………….
Step5: …………………………………….
Và cứ tiếp tục step6, step7, step8 ...

Phép tính tìm kích thước của hình thể phức:

Trong bài Fractals, Meta có nói :” các huyết quản chính tách ra giữa 8 và 30 lần trước khi đến các phần cá biệt trong cơ thể. Hình dạng cực phức của hệ tuần hoàn gần bằng 3 kích thước. Bộ não cũng có cấu trúc với kích thước khoảng 2.79 và 2.73. Chúng ta quá quen thuộc với điểm, đường, mặt phẳng, khối trong hình học cổ điển.” Qua bài Hình Học Siêu Kích Thước, ta đã biết hình thể cực phức tạp luôn trong kích thước lẻ. Kích thước cổ điển gồm:

• Một điểm có zero kích thước.
• Một đường có 1 kích thước, mặt phẳng 2 kích thước gồm dài và rộng
• và cuối cùng là một khối gồm 3 kích thước là dài, rộng và cao.

Kích thước cổ điển thì ta khỏi cần tính, chỉ nhìn là biết. Làm sao tính được kích thước của hình thể phức?

Tính kích thước hình thể cổ điển:

Ta có thể hình dung những kích thước không chẵn như 1.5, 2.79 v.v… sau khi đọc bài Fractals và nhìn những hình ngoằn ngoèo kèm trong bài nhưng chúng ta không biết làm sao tính cho ra con số kích thước lẻ ấy. Ta nhận biết kích thước cổ điển nhờ trực giác nhưng nếu ai thách chúng ta lập công thức thì có khả năng chúng ta bí. Đây là công thức tìm kích thước:

Kích thước = Logn (số bản sao)/ logn (số mỗi cạnh được chia ra)

Một kích thước: Theo hình học cổ điển, đường thẳng có 1 kích thước.

Đây là đường thẳng. Theo công thức trên, ta có 3 bản sao của đường thẳng và vì chỉ có 1 chiều, chiều này được chia làm 3 đoạn. Logn 3/ logn 3 = 1 dimension.

Hai kích thước:

Ta có 9 bản sao và mỗi cạnh được chia làm 3. Dimension = Logn 9 / Logn 3 = 2 dimensions.

Thêm 1 hình vuông nữa cho chắc:

Hình vuông này có 4 bản sao và mỗi cạnh chia làm hai. Dimension = Logn 4 / Logn 2 = 2 dimensions. Như vậy dù ta chia như thế nào, hình vuông cũng chỉ có 2 chiều chẵn chòi.

Thêm 1 hình 2 chiều nữa:

Ta có 64 bản sao (64 hình vuông nhỏ) và mỗi cạnh phân thành 8 đoạn. Dimension = Logn 64 / Logn 8 = 2 dimensions.

Ba kích thước:

Ta có 8 bản sao và mỗi cạnh (dài, rộng, cao)được phân làm 2. Dimension = Logn 8 / Logn 2 = 3 dimensions. Thêm 1 khối nữa cho chắc:

Trong khối này ta có 27 khối nhỏ (tức bản sao) và mỗi cạnh chia làm 3. Dimension = Logn 27 / Logn 3 = 3 dimensions.

Chắc ăn rồi nhé. Như thế liệu công thức trên có áp dụng được để tính kích thước lẻ của Fractals không? Được! Hãy xem dưới đây.

Tính kích thước hình thể phức:

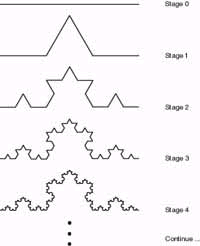
Hình thể von Koch:

Giai đoạn zero, đường thẳng được chia làm 3.

Sang đến giai đoạn 1, nó thành 4 bản sao (4 đoạn nhỏ) và từ đường thẳng ở giai đoạn zero, nó được chia thành 3 phần đều nhau. Theo công thức Kích thước = Logn (số bản sao)/ logn (số mỗi cạnh được chia ra), ta có Dimension = Logn 4 / Logn 3 = 1.2619...

Hình thể Cantor:

Cũng theo công thức trên, giai đoạn thứ nhì, ta có 2 bản sao tuy có 3 phần được chia. Dimension = Logn 2 / Logn 3 = 0.631…

Tam giác Sierpinski:

Một tam giác lớn lấy cái lõi tam giác nhỏ màu trắng còn lại 3 bản sao nhỏ. Mỗi cạnh tam giác lớn được chia làm 2. Dimension = Logn 3 / Logn 2 = 1.585. …

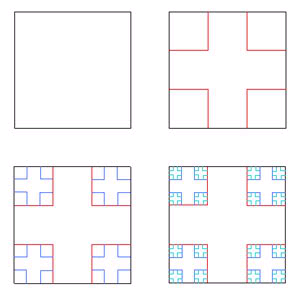
Tấm thảm Sierpinski:

Hình vuông đầu (góc trái phía trên)của tấm thảm này bị khoét 1 lỗ trắng ở giữa. Sau khi chia mỗi cạnh làm 3, nó thành 8 bản sao trong hình vuông đầu. Theo công thức:

Kích thước = Logn (số bản sao)/ logn (số mỗi cạnh được chia ra)

Ta có : Logn 8 / Logn 3 = 1.8927.

Hình thể thập tự vuông:

Khoét cái lõi hình thập tự ở giữa, ta còn lại 4 bản sao hình vuông nhỏ ở 4 góc. Nhìn vào hình vuông nguyên thủy, ta thấy 4 cạnh của nó được chia làm 3 phần đều nhau. Kích thước = Logn bản sao/ Logn sốcạnh bị chia. Ta có: Logn 4 / Logn 3 = 1.2619.

Hình thể khối Meta:

Đây là hình Meta thiết kế, tạm đặt là hình thể Meta:

Có 27 khối nhỏ. Hãy giả dụ khoét đi cái lõi ỡ giữa, vì nó nằm ỡ lõi nên không thấy được nhưng như vậy chỉ còn 26 khối lập phương nhỏ. Mỗi cạnh hình lập phương nguyên thủy được chia làm 3. Ta có:

Logn 26 / Logn 3 = 2.96565. …

Bạn thấy chưa, nó gần đủ 3 chiều, chỉ là 2.96565.

Như thế đã tạm đủ về hình thể cực phức. Nói về Fractals mà không nói đến Chaos and Self-organization, Three-Body Problem, The Edge of Chaos, The Butterfly Effect, Attractors v.v… vẫn là một thiếu sót lớn. Nhưng bài đã dài, xin hẹn gặp lại các bạn trong một dịp khác bàn về đề tài khác, ướt át hơn, thú vị hơn.

Truyện ngắn chẳng hạn.

Metamorph.

Tham khảo

1. http://moscow.cityu.edu.hk/~ma4527/fractal_java/fractal_intro_1.htm
2. http://www.math.utah.edu/~alfeld/math/mandelbrot/mandelbrot.html#algorithm
3. http://www.1728.com/compnum2.htm
4. http://www.ddewey.net/mandelbrot/
5. http://www.math.utah.edu/~alfeld/math/mandelbrot/mandelbrot.html
6. http://nereida.deioc.ull.es/~llCoMP/examples/examples/mandel/mandel_description.html
7. Hyperspace. Book của Michio Kaku
8. Dictionary of Theories. Book của Jennifer Bothamley
9. Who’s afraid of Schrodinger’s cat? Book của Ian Marshall và Danah Zohar, tác giả cuốn The Quantum Self với cộng tác của F. David Peat.

Đọc thêm

• Giới thiệu về hình học Fractal
• Fractal trên Wikipedia tiếng Anh
• Fractal trên Wikipeida tiếng Việt

Bài liên quan

• Tỉ lệ logarit
• Vai trò công cụ của logarit qua một số ứng dụng
• Vài nét sơ lược về lịch sử xuất hiện khái niệm logarit
• Vấn đề dạy học logarit trong chương trình toán phổ thông và những điều cần biết về logarit
• Kẻ thất bại và kẻ siêu thất bại

• « Mới nhất
• ‹ Mới hơn
• Cũ hơn ›

Liên kết đến đây

• Giới thiệu về hình học Fractal