Khảo sát hàm số trong các kì thi tốt nghiệp THPT
Cho
hàm
số
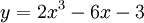
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
2) Viết phương trình tiếp tuyến của đồ thị (C) tại giao điểm của đồ thị (C) với trục tung.
Cho
hàm
số
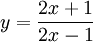
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
2) Xác định tọa độ giao điểm của đồ thị (C) với đường thẳng y = x + 2
Cho
hàm
số
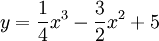
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho
b)
Tìm
các
giá
trị
của
tham
số
m
để
phương
trình
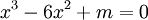 có
3
nghiệm
thực
phân
biệt
có
3
nghiệm
thực
phân
biệt
Cho
hàm
số
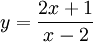
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
2) Viết phương trình tiếp tuyến của đồ thị (C), biết hệ số góc của tiếp tuyến bằng –5.
Cho
hàm
số
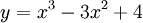 .
.
1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
2. Tìm toạ độ các giao điểm của đồ thị (C) và đường thẳng y = 4.
Cho
hàm
số
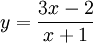 ,
gọi
đồ
thị
của
hàm
số
là
(C).
,
gọi
đồ
thị
của
hàm
số
là
(C).
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho.
2. Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có tung độ bằng -2.
Cho
hàm
số
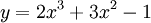 .
.
1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.
2)
Biện
luận
theo
m
số
nghiệm
thực
của
phương
trình
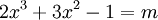 .
.
Cho
hàm
số
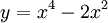 .
.
1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.
2) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = - 2
Cho
hàm
số
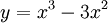 .
.
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho.
2.
Tìm
các
giá
trị
của
tham
số
m
để
phương
trình
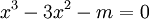 có
ba
nghiệm
phân
biệt.
có
ba
nghiệm
phân
biệt.
Cho
hàm
số
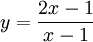 ,
gọi
đồ
thị
của
hàm
số
là
(C).
,
gọi
đồ
thị
của
hàm
số
là
(C).
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho.
2. Viết phương trình tiếp tuyến của đồ thị (C) tại điểm A(2; 3).
Cho
hàm
số
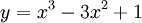 .
.
1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.
2) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = 3.
Cho
hàm
số
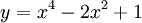 ,
gọi
đồ
thị
của
hàm
số
là
(C).
,
gọi
đồ
thị
của
hàm
số
là
(C).
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số.
2. Viết phương trình tiếp tuyến với đồ thị (C) tại điểm cực đại của (C).
Cho
hàm
số
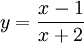 ,
gọi
đồ
thị
của
hàm
số
là
(C).
,
gọi
đồ
thị
của
hàm
số
là
(C).
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số.
2. Viết phương trình tiếp tuyến với đồ thị (C) tại giao điểm của (C) với trục tung.
Cho
hàm
số
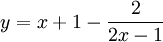 ,
gọi
đồ
thị
của
hàm
số
là
(H).
,
gọi
đồ
thị
của
hàm
số
là
(H).
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số.
2. Viết phương trình tiếp tuyến của đồ thị (H) tại điểm A (0; 3).
Cho
hàm
số
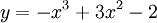 ,
gọi
đồ
thị
của
hàm
số
là
(C).
,
gọi
đồ
thị
của
hàm
số
là
(C).
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số.
2. Viết phương trình tiếp tuyến với đồ thị (C) tại điểm uốn của (C).
Cho
hàm
số
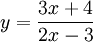 ,
gọi
đồ
thị
của
hàm
số
là
(C).
,
gọi
đồ
thị
của
hàm
số
là
(C).
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số.
2. Viết phương trình tiếp tuyến với đồ thị (C) tại điểm M (1; -7).
Cho
hàm
số
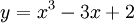 ,
gọi
đồ
thị
của
hàm
số
là
(C).
,
gọi
đồ
thị
của
hàm
số
là
(C).
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số.
2. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm A(2; 4).
1.
Khảo
sát
và
vẽ
đồ
thị
(C)
của
hàm
số
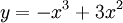 .
.
2.
Dựa
vào
đồ
thị
(C),
biện
luận
theo
m
số
nghiệm
của
phương
trình
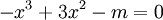 .
.
3. Tính diện tích hình phẳng giới hạn bởi (C) và trục hoành.
1.
Khảo
sát
và
vẽ
đồ
thị
(C)
của
hàm
số
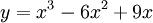 .
.
2. Viết phương trình tiếp tuyến tại điểm uốn của đồ thị (C).
3.
Với
giá
trị
nào
của
tham
số
m,
đường
thẳng
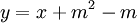 đi
qua
trung
điểm
của
đoạn
thẳng
nối
hai
điểm
cực
đại
và
cực
tiểu
của
đồ
thị
(C).
đi
qua
trung
điểm
của
đoạn
thẳng
nối
hai
điểm
cực
đại
và
cực
tiểu
của
đồ
thị
(C).
1.
Khảo
sát
và
vẽ
đồ
thị
(C)
của
hàm
số
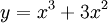 .
.
2. Tính diện tích hình phẳng giới hạn bởi đồ thị (C), trục hoành và các đường thảng x = - 2, x = - 1.
Cho
hàm
số
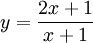 có
đồ
thị
(C)
có
đồ
thị
(C)
1) Khảo sát và vẽ đồ thị hàm số
2) Tính diện tích hình phẳng giới hạn bởi trục tung, trục hoành và đồ thị (C).
3) Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến đó đi qua điểm A(-1;3).
Cho
hàm
số
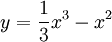 có
đồ
thị
(C).
có
đồ
thị
(C).
1) Khảo sát hàm số
2) Viết phương trình các tiếp tuyến của (C) đi qua điểm A(3; 0).
3) Tính thể tích của vật thể tròn xoay do hình phẳng giới hạn bởi (C) và các đường y = 0, x = 0, x = 3 quay quanh trục Ox.
Cho
hàm
số
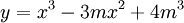 có
đồ
thị
(
có
đồ
thị
(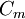 ),
m
là
tham
số
),
m
là
tham
số
1.
Khảo
sát
và
vẽ
đồ
thị
(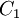 )
của
hàm
số
khi
m
=
1.
)
của
hàm
số
khi
m
=
1.
2.
Viết
phương
trình
tiếp
tuyến
của
đồ
thị
(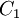 )
tại
điểm
có
hoành
độ
x
=
1.
)
tại
điểm
có
hoành
độ
x
=
1.
3.
Xác
định
m
để
các
điểm
cực
đại
và
cực
tiểu
của
đồ
thị
(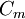 )
đối
xứng
nhau
qua
đường
thẳng
y
=
x.
)
đối
xứng
nhau
qua
đường
thẳng
y
=
x.
Cho
hàm
số
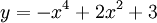 có
đồ
thị
(C).
có
đồ
thị
(C).
1.
Khảo
sát
hàm
số
trên.
2.
Xác
định
m
để
phương
trình
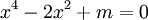 có
4
nghiệm
phân
biệt.
có
4
nghiệm
phân
biệt.
Cho
hàm
số
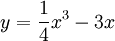 có
đồ
thị
(C).
có
đồ
thị
(C).
1)
Khảo
sát
và
vẽ
đồ
thị
hàm
số.
2)
Cho
điểm
M
thuộc
đồ
thị
(C)
có
hoành
độ
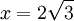 .
Viết
phương
trình
đường
thẳng
d
qua
M
và
là
tiếp
tuyến
của
(C).
.
Viết
phương
trình
đường
thẳng
d
qua
M
và
là
tiếp
tuyến
của
(C).
3) Tính diện tích hình phẳng giới hạn bởi (C) và tiếp tuyến của nó tại điểm M.
Cho
hàm
số
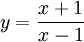 có
đồ
thị
(C).
có
đồ
thị
(C).
1)
Khảo
sát
và
vẽ
đồ
thị
hàm
số.
2) Viết phương trình tiếp tuyến của (C) đi qua A(0; 1). Chứng minh rằng có đúng một tiếp tuyến của (C) qua B(0; -1).
3) Tìm tất cả những điểm có tọa độ nguyên của (C).
Cho
hàm
số
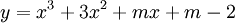 có
đồ
thị
có
đồ
thị
 .
.
1) Khảo sát và vẽ đồ thị (C) của hàm số khi m = 3.
2) Gọi A là giao điểm của (C) và trục tung. Viết phương trình tiếp tuyến của (C) tại A. Tính diện tích hình phẳng giới hạn bởi (C) và tiếp tuyến trên.
3)
Tìm
giá
trị
của
m
để
 cắt
trục
hoành
tại
3
điểm
phân
biệt.
cắt
trục
hoành
tại
3
điểm
phân
biệt.
Cho
hàm
số
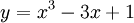 có
đồ
thị
(C).
có
đồ
thị
(C).
1) Khảo sát và vẽ đồ thị (C) của hàm số.
2) Tính diện tích hình phẳng giới hạn bởi đồ thị (C), trục hoành, trục tung và đường thẳng x = -1.
3) Đường thẳng d qua điểm uốn của (C) và có hệ số góc k. Biện luận theo k số giao điểm của (C) và đường thẳng d. Tìm tọa độ giao điểm đó khi k = 1.


