Chủ đề nóng: Phương pháp kỷ luật tích cực - Cổ học tinh hoa - Những thói hư tật xấu của người Việt - Công lý: Việc đúng nên làm - Giáo án Điện tử - Sách giáo khoa - Học tiếng Anh - Bài giảng trực tuyến - Món ăn bài thuốc - Chăm sóc bà bầu - Môi trường - Tiết kiệm điện - Nhi khoa - Ung thư - Tác hại của thuốc lá - Các kỹ thuật dạy học tích cực
- Dạy học phát triển năng lực - Chương trình giáo dục phổ thông
Ôn tập Tốt nghiệp THPT 2009-2010/Khảo sát hàm số và các bài toán liên quan
Từ VLOS
Nội dung khảo sát hàm số và các bài toán liên quan trong cấu trúc đề thi:
Phần chung:
- Khảo sát, vẽ đồ thị của hàm số.
- Các bài toán liên quan đến ứng dụng của đạo hàm và đồ thị của hàm số:
- chiều biến thiên của hàm số;
- cực trị;
- tiếp tuyến;
- tiệm cận (đứng và ngang) của đồ thị hàm số;
- tìm trên đồ thị những điểm có tính chất cho trước;
- tương giao giữa hai đồ thị (một trong hai đồ thị là đường thẳng);...
Phần riêng CTNC:
-
Đồ
thị
hàm
phân
thức
hữu
tỉ
dạng
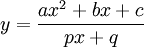 và
một
số
yếu
tố
liên
quan.
và
một
số
yếu
tố
liên
quan.
- Sự tiếp xúc của hai đường cong.
- Xem thêm: Khảo sát hàm số trong các kì thi tốt nghiệp THPT
- Xem thêm: Các bài toán liên quan đến khảo sát trong các kì thi tốt nghiệp THPT
Các bài toán[sửa]
- Chiều biến thiên của hàm số
- Cực trị của hàm số
- Tiếp tuyến của đồ thị hàm số
- Tiệm cận của đồ thị hàm số
- Tương giao giữa hai đồ thị
- Điểm đặc biệt của đồ thị
Sai lầm và cách sửa[sửa]
| Sai | Đúng |
|---|---|
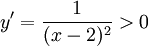
|
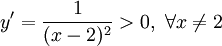
|
|
Hàm
số
nghịch
biến
trên
từng
khoảng:
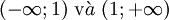
|
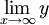 |
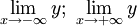 |
| Tìm giới hạn: hàm đa thức, hàm hữu tỉ |
Quy
tắc
tìm
giới
hạn:
|
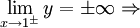 Tiệm
cận
ngang
x
=
1
Tiệm
cận
ngang
x
=
1
|
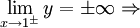 Tiệm
cận
đứng
x
=
1
Tiệm
cận
đứng
x
=
1
|
|
Hàm
số
có
tiệm
cận
ngang
y
=
1
Hàm số có tiệm cận đứng x = 1 |
Đồ
thị
hàm
số
có
tiệm
cận
ngang
y
=
1
Đồ thị hàm số có tiệm cận đứng x = 1 |
Tiếp
tuyến
có
hệ
số
góc
bằng
-5
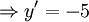
|
Gọi
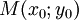 là
tọa
độ
tiếp
điểm
của
(C)
với
tiếp
tuyến
có
hệ
số
góc
là
tọa
độ
tiếp
điểm
của
(C)
với
tiếp
tuyến
có
hệ
số
góc
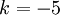 .
.
Thì
|
Hàm
số
đạt
cực
trị
tại
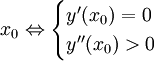
|
Hàm
số
đạt
cực
trị
tại
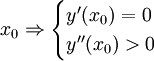
Thử lại ⇒ kết luận |
Hàm
số
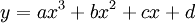 có
cực
trị
có
cực
trị
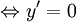 có
2
nghiệm
phân
biệt
có
2
nghiệm
phân
biệt |
Vì
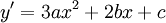 là
tam
thức
bậc
2
nên
hàm
số
là
tam
thức
bậc
2
nên
hàm
số
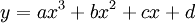 có
cực
trị
có
cực
trị
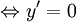 có
2
nghiệm
phân
biệt
có
2
nghiệm
phân
biệt |
Đường
thẳng
(d)
cắt
đồ
thị
(C)
tại
hai
điểm
phân
biệt
 phương
trình
phương
trình
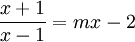 có
hai
nghiệm
phân
biệt
có
hai
nghiệm
phân
biệt
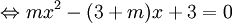 có
hai
nghiệm
phân
biệt
có
hai
nghiệm
phân
biệt
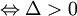
|
Đường
thẳng
(d)
cắt
đồ
thị
(C)
tại
hai
điểm
phân
biệt
 phương
trình
phương
trình
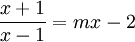 có
hai
nghiệm
phân
biệt
có
hai
nghiệm
phân
biệt
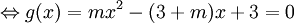 có
hai
nghiệm
phân
biệt
có
hai
nghiệm
phân
biệt
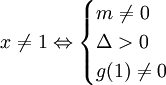
|
Chủ đề khác[sửa]
- Khảo sát hàm số và các bài toán liên quan
- Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
- Hàm số, phương trình, bất phương trình mũ và lôgarit
- Hình học không gian tổng hợp
- Phương pháp tọa độ trong không gian
- Nguyên hàm, tích phân, ứng dụng
- Số phức
<comments
/>
Bài liên quan
Liên kết đến đây
- Ôn tập Tốt nghiệp THPT 2009-2010
- Bản mẫu:Ôn tập Tốt nghiệp THPT 2009-2010
- Ôn tập Tốt nghiệp THPT 2009-2010/Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
- Ôn tập Tốt nghiệp THPT 2009-2010/Hàm số, phương trình, bất phương trình mũ và lôgarit
- Ôn tập Tốt nghiệp THPT 2009-2010/Hình học không gian tổng hợp
- Ôn tập Tốt nghiệp THPT 2009-2010/Phương pháp tọa độ trong không gian
- Ôn tập Tốt nghiệp THPT 2009-2010/Nguyên hàm, tích phân, ứng dụng
- Ôn tập Tốt nghiệp THPT 2009-2010/Số phức
- Ôn tập Tốt nghiệp THPT 2009-2010/Khảo sát hàm số và các bài toán liên quan/1
- Ôn tập Tốt nghiệp THPT 2009-2010/Khảo sát hàm số và các bài toán liên quan/2
- Xem thêm liên kết đến trang này.
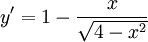
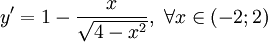
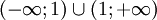
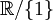
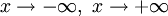
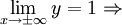 Tiệm
cận
đứng
y
=
1
Tiệm
cận
đứng
y
=
1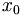 là
nghiệm
của
phương
trình:
là
nghiệm
của
phương
trình: