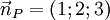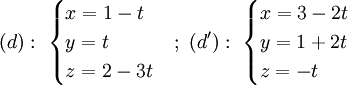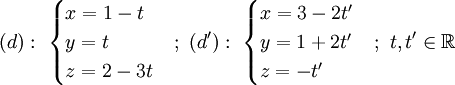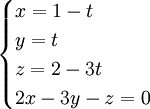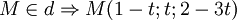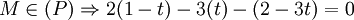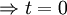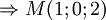Ôn tập Tốt nghiệp THPT 2009-2010/Phương pháp tọa độ trong không gian
Nội dung phương pháp tọa độ trong không gian trong cấu trúc đề thi:
| Chương trình chuẩn | Chương trình nâng cao |
|---|---|
|
- Xác định tọa độ của điểm, vectơ. - Mặt cầu. - Viết phương trình mặt phẳng, đường thẳng. - Tính góc, tính khoảng cách từ điểm đến mặt phẳng. Vị trí tương đối của đường thẳng, mặt phẳng và mặt cầu. |
- Xác định tọa độ của điểm, vectơ. - Mặt cầu. - Viết phương trình mặt phẳng, đường thẳng. - Tính góc; tính khoảng cách từ điểm đến đường thẳng, mặt phẳng; khoảng cách giữa hai đường thẳng; vị trí tương đối của đường thẳng, mặt phẳng và mặt cầu. |
Các dạng toán cần luyện tập
Tính tọa độ của: tổng, hiệu, tích vectơ với một số; Tính được tích vô hướng của hai vectơ; tích có hướng của hai vectơ; Chứng minh bốn điểm không đồng phẳng; Tính thể tích của khối tứ diện;
Tính khoảng cách giữa hai điểm có có tọa độ cho trước; Xác định tọa độ tâm và bán kính mặt cầu có phương trình cho trước; Viết phương trình mặt cầu (biết tâm và đi qua một điểm cho trước, biết đường kính, đi qua một số điểm).
Xác định vectơ pháp tuyến của mặt phẳng. Viết phương trình mặt phẳng. Tính góc. Tính khoảng cách từ một điểm đến một mặt phẳng, tính khoảng cáh giữa hai mặt phẳng song song;
Viết phương trình tham số của đường thẳng (đi qua hai điểm cho trước, đi qua một điểm và song song với một đường thẳng cho trước, đi qua một điểm và vuông góc với một mặt phẳng cho trước). Sử dụng phương trình của hai đường thẳng để xác định vị trí tương đối của hai đường thẳng đó. Tìm hình chiếu vuông góc của một điểm trên một đường thẳng hoặc trên một mặt phẳng.
Toạ độ của điểm, vectơ[sửa]
Lý thuyết[sửa]
Ví dụ[sửa]
Trong không gian với hệ tọa độ Oxyz cho bốn điểm A, B, C, D biết:
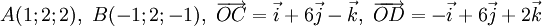
1) Chứng minh rằng: 4 điểm A, B, C, D lập thành một tứ diện có các cặp cạnh đối bằng nhau.
2) Viết phương trình mặt cầu (S) ngoại tiếp hình tứ diện ABCD.
3)* Tính khoảng cách giữa hai đường thẳng AB và CD.
Bài tập tự luyện[sửa]
Phương trình mặt cầu[sửa]
Lý thuyết[sửa]
-
Mặt
cầu
tâm
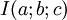 ,
bán
kính
R
có
phương
trình:
,
bán
kính
R
có
phương
trình:
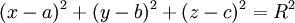
-
Phương
trình
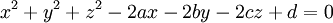 là
phương
trình
mặt
cầu
khi
và
chỉ
khi
là
phương
trình
mặt
cầu
khi
và
chỉ
khi
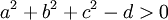
Ví dụ[sửa]
Trong không gian với hệ tọa độ Oxyz, cho hai điểm E(1; -4; 5) và F(3; 2; 7).
1) Viết phương trình mặt cầu có tâm là E và đi qua điểm F.
2) Viết phương trình mặt phẳng trung trực của đoạn thẳng EF.
Trong không gian với hệ tọa độ Oxyz, cho A(2;0;0), B(0;4;0), C(0;0;4).
1) Viết phương trình mặt cầu qua 4 điểm O, A, B, C. Tìm tọa độ tâm I và độ dài bán kính của mặt cầu.
2) Viết phương trình mặt phẳng (ABC). Viết phương trình tham số của đường thẳng qua I và vuông góc với mặt phẳng (ABC).
Trong không gian với hệ tọa độ Oxyz, cho điểm E(1; 2; 3) và mặt phẳng (α) có phương trình x + 2y - 2z + 6 = 0.
1. Viết phương trình mặt cầu (S) có tâm là gốc tọa độ O và tiếp xúc với mặt phẳng (α).
2. Viết phương trình tham số của đường thẳng (Δ) đi qua điểm E và vuông góc với mặt phẳng (α).
Bài tập tự luyện[sửa]
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(2; 0; 0), B(0; 3; 0), C(0; 0; 6).
1) Viết phương trình mặt phẳng đi qua ba điểm A, B, C. Tính diện tích tam giác ABC.
2) Gọi G là trọng tâm tam giác ABC. Viết phương trình mặt cầu đường kính OG.
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(2; 0; 0), B(0; 3; 0), C(0; 0; 6).
1) Viết phương trình mặt phẳng đi qua ba điểm A, B, C. Tính diện tích tam giác ABC.
2) Gọi G là trọng tâm tam giác ABC. Viết phương trình mặt cầu đường kính OG.
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1; -1; 2), B(1; 3; 2), C(4; 3; 2), D(4; -1; 2).
1) Chứng minh rằng A, B, C, D là bốn điểm đồng phẳng.
2) Gọi A' là hình chiếu vuông góc của điểm A trên mặt phẳng Oxy. Hãy viết phương trình mặt cầu (S) đi qua bốn điểm A', B, C, D.
3) Viết phương trình tiếp diện (α) của mặt cầu (S) tại điểm A'.
Trong không gian với hệ tọa độ Oxyz, cho A(3;-2;-2), B(3;2;0), C(0;2;1) và D(-1;1;2).
1) Viết phương trình mặt phẳng qua B, C, D. Suy ra ABCD là tứ diện.
2) Viết phương trình mặt cầu tâm A và tiếp xúc với mặt phẳng (BCD). Tìm tọa độ tiếp điểm.
Phương trình mặt phẳng, đường thẳng[sửa]
Lý thuyết[sửa]
-
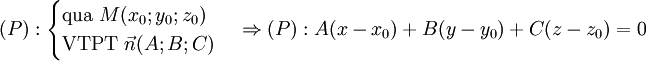
- mp(P) qua A(a; 0; 0), B(0; b; 0), C(0; 0; c), với a.b.c ≠ 0, có phương trình:
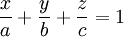
-
mp(Q):
Ax
+
By
+
Cy
+
D
=
0
&
mp(P)
//
mp(Q)
 mp(P):
Ax
+
By
+
Cy
+
E
=
0
với
E
≠
D.
mp(P):
Ax
+
By
+
Cy
+
E
=
0
với
E
≠
D. - Các trường hợp đặc biệt: mp(P) đi qua gốc tọa độ thì phương trình khuyết D. mp(P) // hoặc chứa trục tọa độ nào thì phương trình khuyết ẩn trục đó.
-
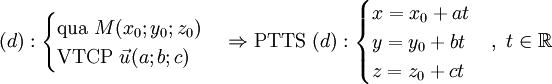
-
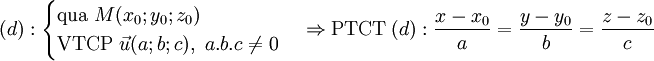
-
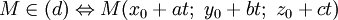
- Hai đường thẳng khác nhau thì hai phương trình tham số phải có tham số khác nhau.
Ví dụ[sửa]
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với A(1; 4; -1), B(2; 4; 3) và C(2; 2; -1).
1) Viết phương trình mặt phẳng đi qua A và vuông góc với đường thẳng BC.
2) Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.
Trong không gian với hệ tọa độ Oxyz, cho ba điểm E(1; 0; 2), M(3; 4; 1) và N(2; 3; 4).
1) Viết phương trình chính tắc của đường thẳng MN.
2) Viết phương trình mặt phẳng đi qua điểm E và vuông góc với đường thẳng MN.
Trong
không
gian
với
hệ
tọa
độ
Oxyz,
cho
hai
điểm
M(1;
0;
2),
N(3;
1;
5)
và
đường
thẳng
(d)
có
phương
trình
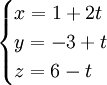
1) Viết phương trình mặt phẳng (P) đi qua điểm M và vuông góc với đường thẳng (d). Tìm tọa độ giao điểm của (P) và (d).
2) Viết phương trình tham số của đường thẳng đi qua hai điểm M và N.
3) Viết phương trình mặt cầu tâm O và tiếp xúc với mp(P).
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(-1; 1; 2), B(0; 1; 1), C(1; 0; 4).
a) Chứng minh tam giác ABC vuông.
b) Viết phương trình tham số của đường thẳng AB.
c)
Gọi
M
là
điểm
sao
cho
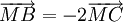 .
Viết
phương
trình
mặt
phẳng
qua
M
và
vuông
góc
với
đường
thẳng
BC.
.
Viết
phương
trình
mặt
phẳng
qua
M
và
vuông
góc
với
đường
thẳng
BC.
Hướng dẫn
a) Nếu dùng định lí Pitago đảo thì phải chứng minh A, B, C không thẳng hàng và bình phương một cạnh bẳng tổng bình phương hai cạnh còn lại.
Bài tập tự luyện[sửa]
Trong không gian Oxyz, cho mặt cầu (S) và mặt phẳng (P) có phương trình:
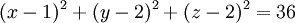 và
(P):
và
(P):
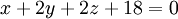 .
.1) Xác định toạ độ tâm T và tính bán kính của mặt cầu (S). Tính khoảng cách từ T đến mặt phẳng (P).
2) Viết phương trình tham số của đường thẳng d đi qua T và vuông góc với (P). Tìm toạ độ giao điểm của d và (P).
Trong không gian với hệ tọa độ Oxyz, cho điểm M(-1; -1; 0) và mặt phẳng (P) có phương trình x + y - 2z - 4 = 0.
1) Viết phương trình mặt phẳng (Q) đi qua điểm M và song song với mặt phẳng (P).
2) Viết phương trình tham số của đường thẳng (d) đi qua điểm M và vuông góc với mặt phẳng (P). Tìm tọa độ giao điểm H của đường thẳng (d) với mặt phẳng (P).
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng (d) và (d') lần lượt có phương trình
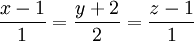 và
(d'):
và
(d'):
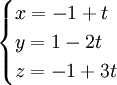
1) Chứng minh rằng hai đường thẳng (d) và (d') vuông góc với nhau.
2) Viết phương trình mặt phẳng đi qua điểm K(1; -2; 1) và vuông góc với đường thẳng (d').
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(-1; 1; 2), B(0; 1; 1), C(1; 0; 4).
1) Chứng minh tam giác ABC vuông. Viết phương trình tham số của đường thẳng AB.
2)
Gọi
M
là
điểm
sao
cho
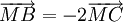 .
Viết
phương
trình
mặt
phẳng
đi
qua
M
và
vuông
góc
với
đường
thẳng
BC.
.
Viết
phương
trình
mặt
phẳng
đi
qua
M
và
vuông
góc
với
đường
thẳng
BC.
Góc, khoảng cách[sửa]
Lý thuyết[sửa]
-
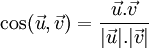
-
Góc
giữa
hai
đường
(d)
và
(d')
lần
lượt
có
hai
vectơ
chỉ
phương
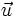 và
và
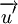 :
:
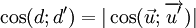
-
Góc
giữa
hai
mặt
phẳng
(P)
và
(Q)
lần
lượt
có
hai
vectơ
pháp
tuyến
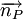 và
và
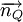 :
:
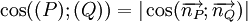
-
Khoảng
cách
từ
điểm
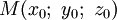 đến
mp(P):
đến
mp(P):
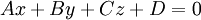 :
:
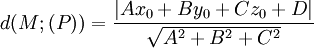
- Khoảng cách giữa đường thẳng (d) tới mặt phẳng (P) song song với nhau ...
- Khoảng cách giữa hai mặt (P) và (Q) song song với nhau ...
- Khoảng cách giữa hai đường thẳng chéo nhau ...
Ví dụ[sửa]
Trong không gian với hệ tọa độ Oxyz, cho các điểm M (1; -2; 0), N (-3; 4; 2) và mặt phẳng (P) có phương trình 2x + 2y + z - 7 = 0.
1. Viết phương trình đường thẳng MN.
2. Tính khoảng cách từ trung điểm của đoạn thẳng MN đến mặt phẳng (P).
Trong không gian với hệ tọa độ Oxyz, cho điểm A (2; - 1; 3) và mặt phẳng (P) có phương trình x - 2y - 2z - 10 = 0.
1. Tính khoảng cách từ điểm A đến mặt phẳng (P).
2. Viết phương trình đường thẳng đi qua điểm A và vuông góc với mặt phẳng (P).
Trong không gian với hệ tọa độ Oxyz, cho điểm A(3; - 2; - 2) và mặt phẳng (P) có phương trình 2x - 2 y + z - 1 = 0.
1) Viết phương trình đường thẳng đi qua điểm A và vuông góc với mặt phẳng (P).
2) Tính khoảng cách từ điểm A đến mặt phẳng (P). Viết phương trình của mặt phẳng (Q) sao cho (Q) song song với (P) và khoảng cách giữa (P) và (Q) bằng khoảng cách từ điểm A đến (P).
Bài tập tự luyện[sửa]
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1; 2; 3) và mặt phẳng (α) có phương trình 2x - 3y + 6z + 35 = 0.
1) Viết phương trình đường thẳng đi qua điểm M và vuông góc với mặt phẳng (α).
2) Tính khoảng cách từ điểm M đến mặt phẳng (α). Tìm tọa độ điểm N thuộc trục Ox sao cho độ dài đoạn thẳng NM bằng khoảng cách từ điểm M đến mặt phẳng (α).
Trong không gian với hệ tọa độ Oxyz, cho điểm M(-1; 2; 3) và mặt phẳng (α) có phương trình x - 2 y + 2z + 5 = 0.
1) Viết phương trình đường thẳng đi qua điểm M và vuông góc với mặt phẳng (α).
2) Viết phương trình mặt phẳng (β) đi qua điểm M và song song với mặt phẳng (α). Tính khoảng cách giữa hai mặt phẳng (α) và (β).
Trong không gian với hệ tọa độ Oxyz, cho hình hộp chữ nhật có các đỉnh A(3;0;0), B(0;4;0), C(0;0;5), O(0;0;0) và đỉnh D là đỉnh đối diện của O.
1) Tìm tọa độ điểm D và viết phương trình mặt phẳng (ABD).
2) Viết phương trình đường thẳng (d) qua C và vuông góc với mặt phẳng (ABD).
3) Tính khoảng cách từ C tới mặt phẳng (ABD).
Tương giao giữa đường thẳng, mặt phẳng, mặt cầu[sửa]
Lý thuyết[sửa]
1)
Cho
hai
đường
thẳng
d
và
d'
lần
lượt
có
vecto
chỉ
phương
 và
và
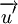
-
d
//
d'

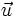 và
và
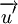 cùng
phương
&
M
∈
d,
M
∉
d'
cùng
phương
&
M
∈
d,
M
∉
d'

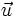 và
và
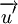 &
Hệ
pt
2
tham
số
vô
nghiệm
&
Hệ
pt
2
tham
số
vô
nghiệm
-
d
≡
d'

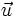 và
và
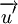 cùng
phương
&
M
∈
d,
M
∈
d'
cùng
phương
&
M
∈
d,
M
∈
d'

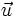 và
và
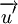 &
Hệ
pt
2
tham
số
vô
số
nghiệm
&
Hệ
pt
2
tham
số
vô
số
nghiệm
-
d
∩
d'
 Hệ
pt
2
tham
số
có
nghiệm
duy
nhất.
Hệ
pt
2
tham
số
có
nghiệm
duy
nhất.
-
d
chéo
d'

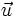 và
và
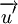 không
cùng
phương
&
Hệ
pt
2
tham
số
vô
nghiệm
không
cùng
phương
&
Hệ
pt
2
tham
số
vô
nghiệm
2)
Cho
đường
thẳng
d
và
mặt
phẳng
(P)
lần
lượt
có
vecto
chỉ
phương
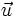 và
vecto
pháp
tuyến
và
vecto
pháp
tuyến
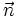
-
d
//
(P)
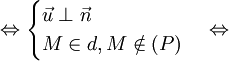 Hệ
Hệ
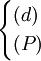 vô
nghiệm.
vô
nghiệm.
-
d
∩
(P)
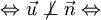 Hệ
Hệ
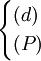 có
nghiệm
duy
nhất.
có
nghiệm
duy
nhất.
-
d
⊂
(P)
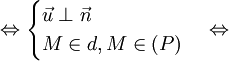 Hệ
Hệ
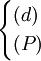 vô
số
nghiệm.
vô
số
nghiệm.
3) Cho mp(P) và mặt cầu (S) có tâm I và bán kính R
-
(P)
cắt
(S)
 d(I;
(P))
<
R
d(I;
(P))
<
R
-
(P)
tiếp
xúc
(S)
 d(I;
(P))
=
R
d(I;
(P))
=
R
-
(P)
và
(S)
không
có
điểm
chung
 d(I;
(P))
>
R
d(I;
(P))
>
R
Ví dụ[sửa]
Trong không gian với hệ tọa độ Oxyz, cho điểm F(1; 2; 3) và mp(α): x + 2y - 2z + 6 = 0.
a) Viết phương trình mặt cầu (S) có tâm là gốc tọa độ và tiếp xúc với mặt phẳng (α).
b) Viết phương trình tham số của đường thẳng Δ đi qua E và vuông góc với (α). Tìm tọa độ giao điểm của Δ với (α).
Trong không gian với hệ tọa độ Oxyz, cho điểm A(2; 0; 0), B(0; 3; 0), C(0; 0; 6).
a) Viết phương trình mặt phẳng đi qua 3 điểm A, B, C.
b) Gọi G là trọng tâm tam giác ABC. Viết phương trình tham số, phương trình chính tắc (nếu có) của đường thẳng OG.
c) Viết phương trình mặt cầu đường kính OG.
Trong không gian với hệ tọa độ Oxyz, cho điểm A(4; 3; 2), B(3; 0; 0), C(0; 3; 0) và D(0; 0; 3).
a) Viết phương trình đường thẳng đi qua A và trọng tâm G của tam giác BCD.
b) Viết phương trình mặt phẳng qua G và vuông góc với AG.
c) Viết phương trình mặt cầu tâm A và tiếp xúc với mặt phẳng đi qua ba điểm B, C, D.
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1; 0; -1), B(1; 2; 1), C(0; 2; 0). Gọi G là trọng tâm tam giác ABC.
1) Viết phương trình đường thẳng OG.
2) Viết phương trình mặt cầu (S) đi qua bốn điểm O, A, B, C.
3) Viết phương trình các mặt phẳng vuông góc với đường thẳng OG và tiếp xúc với mặt cầu (S).
Bài tập tự luyện[sửa]
Trong
không
gian
với
hệ
tọa
độ
Oxyz,
cho
điểm
M
(
-2;
1;
-
2
)
và
đường
thẳng
d
có
phương
trình
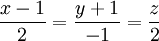
1. Chứng minh rằng đường thẳng OM song song với đường thẳng d.
2. Viết phương trình mặt phẳng đi qua điểm M và vuông góc với đường thẳng d.
Trong
không
gian
với
hệ
tọa
độ
Oxyz,
cho
điểm
M(1;
-2;
0)
và
đường
thẳng
d
có
phương
trình
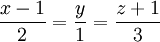 .
.
1) Tìm tọa độ giao điểm của đường thẳng d với mặt phẳng có phương trình 2x - y + z - 7 = 0.
2) Viết phương trình mặt phẳng đi qua điểm M và vuông góc với đường thẳng d.
Trong
không
gian
với
hệ
tọa
độ
Oxyz,
cho
đường
thẳng
(d)
có
phương
trình
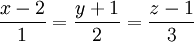 và
mặt
phẳng
(P)
có
phương
trình
x
-
y
+
3z
+
2
=
0.
và
mặt
phẳng
(P)
có
phương
trình
x
-
y
+
3z
+
2
=
0.
1) Tìm tọa độ giao điểm M của đường thẳng (d) với mặt phẳng (P).
2) Viết phương trình mặt phẳng chứa đường thẳng (d) và vuông góc với mặt phẳng (P).
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(0; 2; 1), B(1; -1; 3) và mặt phẳng (P) có phương trình 2x + y + 3z = 0.
1) Viết phương trình tham số của đường thẳng AB.
2) Tìm tọa độ giao điểm M của đường thẳng AB với mặt phẳng (P).
Trong
không
gian
với
hệ
tọa
độ
Oxyz,
cho
mặt
cầu
(S):
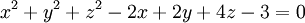 và
hai
đường
thẳng
và
hai
đường
thẳng
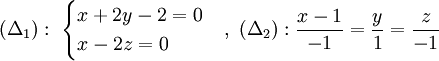
1)
Chứng
minh
(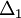 )
và
(
)
và
(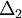 )
chéo
nhau.
)
chéo
nhau.
2)
Viết
phương
trình
tiếp
diện
của
mặt
cầu
(S),
biết
tiếp
diện
đó
song
song
với
hai
đường
thẳng
(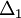 )
và
(
)
và
(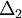 ).
).
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) và đường thẳng d lần lượt có phương trình:
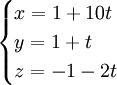 với
với
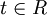
1) Tìm tọa độ giao điểm A của đường thẳng d với mặt phẳng (P).
2)
Cho
đường
thẳng
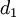 có
phương
trình
có
phương
trình
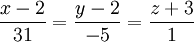 .
Chứng
minh
hai
đường
thẳng
.
Chứng
minh
hai
đường
thẳng
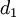 và
d
chéo
nhau.
Viết
phương
trình
mặt
phẳng
(Q)
chứa
đường
thẳng
d
và
song
song
với
đường
thẳng
và
d
chéo
nhau.
Viết
phương
trình
mặt
phẳng
(Q)
chứa
đường
thẳng
d
và
song
song
với
đường
thẳng
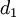 .
.
3) Viết phương trình chính tắc của đường thẳng Δ là giao tuyến của hai mặt phẳng (P) và (Q).
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A, B, C, D có tọa độ xác định bởi các hệ thức:
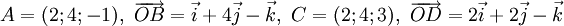
1) Chứng minh rằng AB ⊥ AC, AC ⊥ AD, AD ⊥ AB. Tính thể tích khối tứ diện ABCD.
2) Viết phương trình tham số của đường vuông góc chung Δ của hai đường thẳng AB và CD. Tính góc giữa đường thẳng Δ và mặt phẳng (ABCD).
3) Viết phương trình mặt cầu (S) đi qua bốn điểm A, B, C, D. Viết phương trình tiếp diện (α) của mặt cầu (S) song song với mặt phẳng (ABD).
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x + y + z - 1 = 0. Mặt phẳng (P) cắt các trục tọa độ Ox, Oy, Oz lần lượt tại A, B, C.
1.
Tìm
tọa
độ
A,
B,
C.
Viết
phương
trình
giao
tuyến
của
(P)
với
các
mặt
tọa
độ.
Tìm
tọa
độ
giao
điểm
D
của
đường
thẳng
(d):
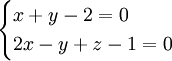 với
mặt
phẳng
Oxy.
Tính
thể
tích
tứ
diện
ABCD.
với
mặt
phẳng
Oxy.
Tính
thể
tích
tứ
diện
ABCD.
2. Viết phương trình mặt cầu (S) ngoại tiếp tứ diện ABCD. Viết phương trình đường tròn ngoại tiếp tam giác ACD. Xác định tâm và bán kính của đường tròn đó.
Trong
không
gian
với
hệ
tọa
độ
Oxyz,
cho
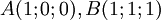 và
và
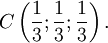
1)
Viết
phương
trình
mặt
phẳng
(P)
vuông
góc
với
OC
tại
C.
Chứng
minh
O,
B,
C
thẳng
hàng.
Xét
vị
trí
tương
đối
của
mặt
cầu
(S)
tâm
B,
bán
kính
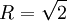 với
mặt
phẳng
(P).
với
mặt
phẳng
(P).
2) Viết phương trình tổng quát của đường thẳng d là hình chiếu vuông góc của đường thẳng AB lên mặt phẳng (P).
Trong
không
gian
với
hệ
tọa
độ
Oxyz,
cho
mặt
phẳng
(P):
2x
-
3y
+
4z
-
5
=
0
và
mặt
cầu
(S):
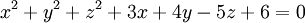
1) Tìm tọa độ tâm I và bán kính của mặt cầu (S).
2) Tính khoảng cách từ I tới mặt phẳng(P), từ đó suy ra rằng (P) cắt mặt cầu theo một đường tròn (C). Hãy tính tọa độ tâm H và bán kính r của (C).
Sai lầm và cách sửa[sửa]
| Sai | Đúng |
|---|---|
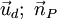 |
Đường
thẳng
d
có
vectơ
chỉ
phương
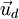
Mặt
phẳng
(P)
có
vectơ
pháp
tuyến
Gọi
Đường
thẳng
cần
tìm
vuông
góc
với
mp(P)
nên
nhận
|
Mặt
phẳng
(P)
có
vectơ
pháp
tuyến
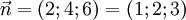
|
Mặt
phẳng
(P)
có
một
vectơ
pháp
tuyến
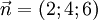
Mặt
phẳng
(P)
có
một
vectơ
pháp
tuyến
|
|
Đường
thẳng
d
và
d'
lần
lượt
có
phương
trình:
|
Đường
thẳng
d
và
d'
lần
lượt
có
phương
trình:
|
|
Tọa
độ
giao
điểm
của
đường
thẳng
d
và
mp(P)
là
nghiệm
của
hệ:
|
Gọi
M
là
giao
điểm
của
d
và
mp(P).
Ta
có:
|
|
Phương
trình
mặt
cầu
(S)
có
dạng:
|
Phương
trình
mặt
cầu
(S)
có
dạng:
|
| d: M --> (P) = | d(M; (P)) = |
Chủ đề khác[sửa]
- Khảo sát hàm số và các bài toán liên quan
- Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
- Hàm số, phương trình, bất phương trình mũ và lôgarit
- Hình học không gian tổng hợp
- Phương pháp tọa độ trong không gian
- Nguyên hàm, tích phân, ứng dụng
- Số phức
<comments
/>
Bài liên quan
Liên kết đến đây
- Ôn tập Tốt nghiệp THPT 2009-2010
- Ôn tập Tốt nghiệp THPT 2009-2010/Khảo sát hàm số và các bài toán liên quan
- Bản mẫu:Ôn tập Tốt nghiệp THPT 2009-2010
- Ôn tập Tốt nghiệp THPT 2009-2010/Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
- Ôn tập Tốt nghiệp THPT 2009-2010/Hàm số, phương trình, bất phương trình mũ và lôgarit
- Ôn tập Tốt nghiệp THPT 2009-2010/Hình học không gian tổng hợp
- Ôn tập Tốt nghiệp THPT 2009-2010/Nguyên hàm, tích phân, ứng dụng
- Ôn tập Tốt nghiệp THPT 2009-2010/Số phức
- Ôn tập Tốt nghiệp THPT 2009-2010/Khảo sát hàm số và các bài toán liên quan/1
- Ôn tập Tốt nghiệp THPT 2009-2010/Khảo sát hàm số và các bài toán liên quan/2
- Xem thêm liên kết đến trang này.
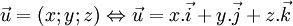
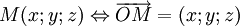
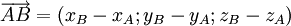
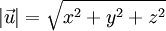
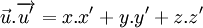
![\left[{\vec u},{\vec v}\right]=\left({\begin{vmatrix}y&z\\y'&z'\end{vmatrix}};{\begin{vmatrix}z&x\\z'&x'\end{vmatrix}};{\begin{vmatrix}x&y\\x'&y'\end{vmatrix}}\right)](https://tusach.thuvienkhoahoc.com/images/math/b/5/8/b58eef15d17dffdd89872a1432ffd49a.png)
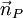
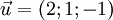
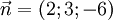 là
một
vectơ
chỉ
phương.
là
một
vectơ
chỉ
phương.