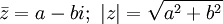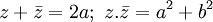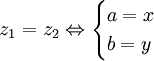Chủ đề nóng: Phương pháp kỷ luật tích cực - Cổ học tinh hoa - Những thói hư tật xấu của người Việt - Công lý: Việc đúng nên làm - Giáo án Điện tử - Sách giáo khoa - Học tiếng Anh - Bài giảng trực tuyến - Món ăn bài thuốc - Chăm sóc bà bầu - Môi trường - Tiết kiệm điện - Nhi khoa - Ung thư - Tác hại của thuốc lá - Các kỹ thuật dạy học tích cực
- Dạy học phát triển năng lực - Chương trình giáo dục phổ thông
Ôn tập Tốt nghiệp THPT 2009-2010/Số phức
Từ VLOS
Nội dung số phức trong cấu trúc đề thi:
| Chương trình chuẩn | Chương trình nâng cao |
|---|---|
| Môđun của số phức, các phép toán trên số phức; căn bậc hai của số thực âm; phương trình bậc hai hệ số thực có biệt thức Δ âm. | Môđun của số phức, các phép toán trên số phức; căn bậc hai của số phức; phương trình bậc hai với hệ số phức; dạng lượng giác của số phức. |
- Xem thêm: Số phức trong các kì thi tốt nghiệp THPT
Lý thuyết[sửa]
+
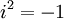
+
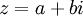 (với
a,
b
∈
R)
(với
a,
b
∈
R)
+ Các phép toán trên số phức: cộng, trừ, nhân, chia
+
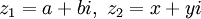
+ Điểm M(x; y) là điểm biểu diễn của số phức z = x + yi
+
Giải
phương
trình
bậc
2
trên
tập
số
phức:
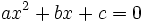 (a,
b,
c
∈
R;
a
≠
0)
(a,
b,
c
∈
R;
a
≠
0)
-
Tính
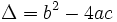
-
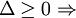 phương
trình
có
hai
nghiệm
thực
phương
trình
có
hai
nghiệm
thực
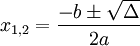
-
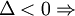 phương
trình
có
hai
nghiệm
phức
phương
trình
có
hai
nghiệm
phức
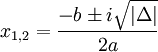
+ Trên tập ℂ, phương trình đa thức bậc n với các hệ số thực luôn có n nghiệm phân biệt.
Ví dụ[sửa]
Tính
giá
trị
biểu
thức
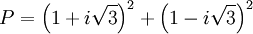
Giải các phương trình sau trên tập số phức:
a)
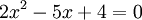
b)
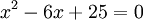
c)
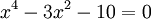
d)
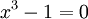
Tìm phần thực, phần ảo của số phức
Tính modun của số phức
Tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ biết
a)
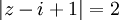 .
.
b)
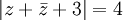
Bài tập tự luyện[sửa]
- Xem thêm: Số phức trong các kì thi tốt nghiệp THPT
Sai lầm và cách sửa[sửa]
| Sai | Đúng |
|---|---|
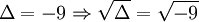 |
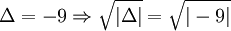 |
Trên
tập
ℂ,
phương
trình
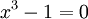 có
một
nghiệm
x
=
1.
có
một
nghiệm
x
=
1. |
Trên
tập
ℂ,
phương
trình
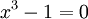 có
3
nghiệm
phân
biệt
có
3
nghiệm
phân
biệt
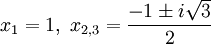
|
Chủ đề khác[sửa]
- Khảo sát hàm số và các bài toán liên quan
- Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
- Hàm số, phương trình, bất phương trình mũ và lôgarit
- Hình học không gian tổng hợp
- Phương pháp tọa độ trong không gian
- Nguyên hàm, tích phân, ứng dụng
- Số phức
<comments
/>
Bài liên quan
Liên kết đến đây
- Ôn tập Tốt nghiệp THPT 2009-2010
- Ôn tập Tốt nghiệp THPT 2009-2010/Khảo sát hàm số và các bài toán liên quan
- Bản mẫu:Ôn tập Tốt nghiệp THPT 2009-2010
- Ôn tập Tốt nghiệp THPT 2009-2010/Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
- Ôn tập Tốt nghiệp THPT 2009-2010/Hàm số, phương trình, bất phương trình mũ và lôgarit
- Ôn tập Tốt nghiệp THPT 2009-2010/Hình học không gian tổng hợp
- Ôn tập Tốt nghiệp THPT 2009-2010/Phương pháp tọa độ trong không gian
- Ôn tập Tốt nghiệp THPT 2009-2010/Nguyên hàm, tích phân, ứng dụng
- Ôn tập Tốt nghiệp THPT 2009-2010/Khảo sát hàm số và các bài toán liên quan/1
- Ôn tập Tốt nghiệp THPT 2009-2010/Khảo sát hàm số và các bài toán liên quan/2
- Xem thêm liên kết đến trang này.