Ôn tập Tốt nghiệp THPT 2009-2010/Hình học không gian tổng hợp
Nội dung hình không gian tổng hợp trong cấu trúc đề thi:
Diện tích xung quanh của hình nón tròn xoay, hình trụ tròn xoay; tính thể tích khối lăng trụ, khối chóp, khối nón tròn xoay, khối trụ tròn xoay; diện tích mặt cầu và thể tích khối cầu.
Hình chóp đều[sửa]
Lý thuyết[sửa]
Định nghĩa 1: Đáy đều & các cạnh bên bằng nhau
Định nghĩa 2: Đáy đều & hình chiếu vuông góc của đỉnh trùng với tâm đáy
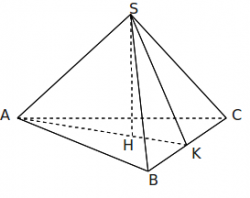
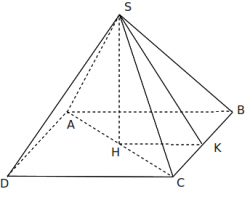
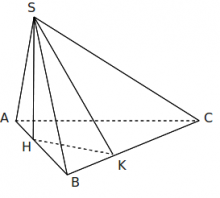
Xét hình chóp tam giác đều S.ABC và hình chóp tứ giác đều S.ABCD.
Hình vẽ minh họa
Cách xác định: đường cao, góc, mặt cầu ngoại tiếp
+ Gọi H là tâm đáy => H là hình chiếu vuông của S trên đáy ==> SH là đường cao của hình chóp
+ ∠(SA;(ABC)) = ∠SAH
+ ∠((SBC);(ABC)) = ?
- Kẻ HK vuông góc với BC tại K. (1)
- Mà SH ⊥ (ABC) => SH ⊥ BC. (2)
- (1)(2) => BC ⊥ mp(SHK) => BC ⊥ SK. (3)
- (1)(3) => ∠((SBC);(ABC)) = ∠SKH
Ví dụ[sửa]
Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên 2a. Gọi I là trung điểm BC.
a) Chứng minh rằng SA ⊥ BC
b)
Tính
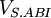 theo
a.
theo
a.
c) Tính tan((SAB),(ABC))?
Bài tập tự luyện[sửa]
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, cạnh bên bằng 2a. Gọi I là trung điểm của cạnh BC.
1) Chứng minh SA vuông góc với BC
2) Tính thể tích của khối chóp S.ABI theo a.
Hình chóp một cạnh bên vuông đáy[sửa]
Lý thuyết[sửa]
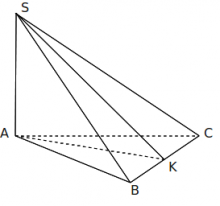
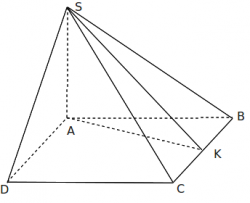
Xét hình chóp S.ABC và S.ABCD có cạnh bên SA vuông góc với mặt phẳng đáy.
Hình vẽ minh họa:
Cách xác định: đường cao, góc, mặt cầu ngoại tiếp
+ SA ⊥ (ABC) => SA là đường cao của hình chóp
+ ∠(SB;(ABC)) = ∠SBA
+ ∠((SBC);(ABC)) = ?
- Kẻ AK ⊥ BC tại K. (1)
- Mà BC ⊥ SA, vì SA ⊥ (ABC). (2)
- (1)(2) => BC ⊥ (SAK) => BC ⊥ SK. (3)
- (1)(3) => ∠((SBC);(ABC)) = ∠SKA
Ví dụ[sửa]
Cho
hình
chóp
S.ABC
có
mặt
bên
SBC
là
tam
giác
đều
cạnh
a,
cạnh
bên
SA
vuông
góc
với
mặt
phẳng
đáy.
Biết
góc
BAC
=
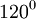 ,
tính
thể
tích
của
khối
chóp
S.ABC
theo
a.
,
tính
thể
tích
của
khối
chóp
S.ABC
theo
a.
Cho
hình
chóp
S.ABCD
có
đáy
ABCD
là
hình
vuông
cạnh
a,
cạnh
bên
SA
vuông
góc
với
đáy,
cạnh
bên
SB
bằng
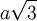 .
.
1) Tính thể tích của khối chóp S.ABCD
2) Chứng minh trung điểm của cạnh SC là tâm mặt cầu ngoại tiếp hình chóp S.ABCD
Hướng dẫn
2) Cách 1: Chứng minh trung điểm của SC cách đều các đỉnh hình chóp. Cách 2: Chứng minh các điểm A, B, D cùng nhìn SC dưới một góc vuông.
Bài tập tự luyện[sửa]
Cho
hình
chóp
S.ABC
có
đáy
là
tam
giác
ABC
vuông
góc
tại
B,
đường
thẳng
SA
vuông
góc
với
mặt
phẳng
(ABC).
Biết
AB
=
a,
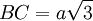 và
SA
=
3a.
và
SA
=
3a.
1) Tính thể tích của khối chóp S.ABC theo a.
2) Gọi I là trung điểm của cạnh SC, tính độ dài đoạn thẳng BI theo a.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông đỉnh B, cạnh bên SA vuông góc với đáy. Biết SA = AB = BC = a. Tính thể tích của khối chóp S.ABC.
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng a, cạnh bên SA vuông góc với đáy và SA = AC. Tính thể tích của khối chóp S.ABCD
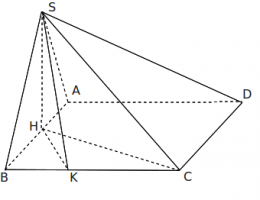
Hình chóp một mặt bên vuông đáy[sửa]
Lý thuyết[sửa]
Định lí: Cho hai mặt phẳng vuông góc, nếu đường thẳng nào nằm trong mặt phẳng này mà vuông vuông góc với giao tuyến thì sẽ vuông góc với mặt phẳng kia.
Xét hai hình chóp S.ABC và S.ABCD có mặt bên (SAB) ⊥ (ABC) = AB. (1)
Hình vẽ minh họa:
Cách xác định: đường cao, góc, mặt cầu ngoại tiếp
+ Đường cao?
- Gọi SH là đường cao của tam giác SAB => SH ⊥ AB. (2)
- (1)(2) => SH ⊥ (ABC) => SH là đường cao của hình chóp
+ ∠(SC;(ABC))= ∠SCH
+ ∠((SBC);(ABC)) = ?
- Kẻ HK ⊥ BC = K (3)
- Mà BC ⊥ SH, vì SH ⊥ (ABC). (4)
- (3)(4) => BC ⊥ (SHK) => BC ⊥ SK (5)
- (3)(5) => ∠((SBC);(ABC)) = ∠SKH
Ví dụ[sửa]
Cho
hình
chóp
S.ABC
có
đáy
ABC
là
tam
giác
vuông
tại
A,
AB
=
a,
AC
=
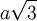 ,
mặt
bên
SBC
là
tam
giác
đều
và
vuông
góc
với
mặt
phẳng
đáy.
,
mặt
bên
SBC
là
tam
giác
đều
và
vuông
góc
với
mặt
phẳng
đáy.
a) Tính thể tích của khối chóp S.ABC.
b) Tính tan((SBC);(ABC))
Bài tập tự luyện[sửa]
Cho
hình
chóp
S.ABC,
mặt
phẳng
(SAB)
vuông
góc
với
đáy,
tam
giác
SAB
cân
S.
Tam
giác
ABC
đều
cạnh
a,
cạnh
SA
tạo
với
đáy
một
góc
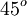 .
Tính
thể
tích
hình
chóp
S.ABC
theo
a.
.
Tính
thể
tích
hình
chóp
S.ABC
theo
a.
Lăng trụ thường gặp[sửa]
Lý thuyết[sửa]
Hình vẽ minh họa:
Cách xác định: chiều cao, góc, mặt cầu ngoại tiếp
Ví dụ[sửa]
Cho hình lăng trụ ABC.A'B'C' có tất cả các cạnh đều bằng a. Tính thể tích của lăng trụ đã cho và diện tích mặt cầu ngoại tiếp hình lăng trụ.
Mặt cầu, mặt nón, mặt trụ[sửa]
Lý thuyết[sửa]
| Khối |
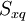 |
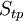 |
V | Hình minh họa |
|---|---|---|---|---|
| Cầu |
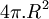 |
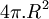 |
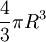 |
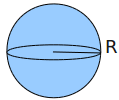 |
| Nón |
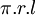 |
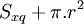 |
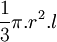 |
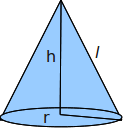 |
| Trụ |
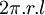 |
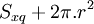 |
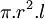 |
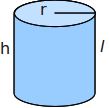 |
Ví dụ[sửa]
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, SA = 2a.
1) Tính diện tích, thể tích của mặt cầu ngoại tiếp hình chóp S.ABCD
2) Kẻ AH vuông góc với SC tại H. Chứng minh rằng: H, A, B, C, D nằm trên một mặt cầu.
Cho
hình
nón
có
bán
kính
đáy
là
R,
góc
tạo
bởi
đường
cao
và
đường
sinh
là
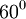 .
.
1) Hãy tính diện tích thiết diện cắt hình nón theo hai đường sinh vuông góc với nhau.
2) Tính diện tích xung quanh của mặt nón và thể tích của khối nón.
Một hình trụ có diện tích xung quanh là S, diện tích đáy bằng diện tích một mặt càu bán kính bằng a.
1) Tính diện tích toàn phần và thể tích của khối trụ.
2) Tính diện tích thiết diện qua trục của hình trụ.
Bài tập tự luyện[sửa]
Sai lầm và cách sửa[sửa]
Chủ đề khác[sửa]
- Khảo sát hàm số và các bài toán liên quan
- Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
- Hàm số, phương trình, bất phương trình mũ và lôgarit
- Hình học không gian tổng hợp
- Phương pháp tọa độ trong không gian
- Nguyên hàm, tích phân, ứng dụng
- Số phức
<comments
/>
Bài liên quan
Liên kết đến đây
- Ôn tập Tốt nghiệp THPT 2009-2010
- Ôn tập Tốt nghiệp THPT 2009-2010/Khảo sát hàm số và các bài toán liên quan
- Bản mẫu:Ôn tập Tốt nghiệp THPT 2009-2010
- Ôn tập Tốt nghiệp THPT 2009-2010/Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
- Ôn tập Tốt nghiệp THPT 2009-2010/Hàm số, phương trình, bất phương trình mũ và lôgarit
- Ôn tập Tốt nghiệp THPT 2009-2010/Phương pháp tọa độ trong không gian
- Ôn tập Tốt nghiệp THPT 2009-2010/Nguyên hàm, tích phân, ứng dụng
- Ôn tập Tốt nghiệp THPT 2009-2010/Số phức
- Ôn tập Tốt nghiệp THPT 2009-2010/Khảo sát hàm số và các bài toán liên quan/1
- Ôn tập Tốt nghiệp THPT 2009-2010/Khảo sát hàm số và các bài toán liên quan/2
- Xem thêm liên kết đến trang này.