Ôn tập Tốt nghiệp THPT 2009-2010/Nguyên hàm, tích phân, ứng dụng
Nội dung nguyên hàm, tích phân, ứng dụng trong cấu trúc đề thi:
Phần chung: Tìm nguyên hàm, tính tích phân
Phần riêng: Ứng dụng của tích phân: tính diện tích hình phẳng, thể tích khối tròn xoay.
Phương pháp tính[sửa]
Lý thuyết[sửa]
+ Áp dụng định nghĩa, tính chất và bảng nguyên hàm.
+ Phương pháp đổi biến số u = u(x)
+ Phương pháp từng phần
Ví dụ[sửa]
Tính các tích phân
Bài tập tự luyện[sửa]
Ứng dụng[sửa]
Lý thuyết[sửa]
+ Tính diện tích
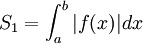
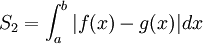
+ Tính thể tích khối tròn xoay
![V=\pi \int _{a}^{b}[f(x)]^{2}dx](https://tusach.thuvienkhoahoc.com/images/math/e/2/1/e21201884291d87797138cd7b4d603bf.png)
Ví dụ[sửa]
Tính diện tích hình phẳng giới hạn bởi
a)
Đồ
thị
hàm
số
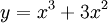 ,
trục
hoành,
x
=
-2
và
x
=
-1.
,
trục
hoành,
x
=
-2
và
x
=
-1.
b)
Đồ
thị
hàm
số
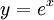 ,
y
=
2
và
x
=
1
,
y
=
2
và
x
=
1
c)
Đồ
thị
hàm
số
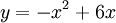 và
trục
hoành
và
trục
hoành
Tính thể tích của khối tròn xoay sinh bởi hình phẳng (H) khi quay quanh trục hoành. Biết (H) giới hạn bởi các đường y = sin x, y = 0, x = 0 và x = π/2.
Bài tập tự luyện[sửa]
Sai lầm và cách sửa[sửa]
| Sai | Đúng |
|---|---|
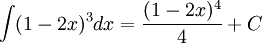 |
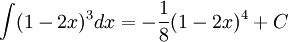 |
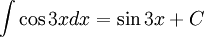
|
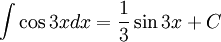
|
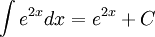 |
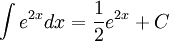 |
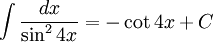 |
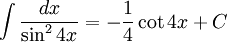 |
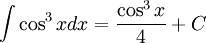 |
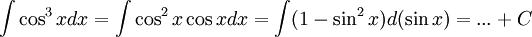 |
Tính
diện
tích
hình
phẳng
giới
hạn
bởi:
đồ
thị
hàm
số
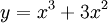 ,
trục
hoành,
x
=
-2
và
x
=
1.
,
trục
hoành,
x
=
-2
và
x
=
1. |
|
|
Lời
giải
|
Lời
giải:
Hoành độ giao điểm của đồ thị và trục hoành là nghiệm của phương trình 
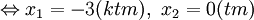
|
Chủ đề khác[sửa]
- Khảo sát hàm số và các bài toán liên quan
- Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
- Hàm số, phương trình, bất phương trình mũ và lôgarit
- Hình học không gian tổng hợp
- Phương pháp tọa độ trong không gian
- Nguyên hàm, tích phân, ứng dụng
- Số phức
<comments
/>
Bài liên quan
Liên kết đến đây
- Ôn tập Tốt nghiệp THPT 2009-2010
- Ôn tập Tốt nghiệp THPT 2009-2010/Khảo sát hàm số và các bài toán liên quan
- Bản mẫu:Ôn tập Tốt nghiệp THPT 2009-2010
- Ôn tập Tốt nghiệp THPT 2009-2010/Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
- Ôn tập Tốt nghiệp THPT 2009-2010/Hàm số, phương trình, bất phương trình mũ và lôgarit
- Ôn tập Tốt nghiệp THPT 2009-2010/Hình học không gian tổng hợp
- Ôn tập Tốt nghiệp THPT 2009-2010/Phương pháp tọa độ trong không gian
- Ôn tập Tốt nghiệp THPT 2009-2010/Số phức
- Ôn tập Tốt nghiệp THPT 2009-2010/Khảo sát hàm số và các bài toán liên quan/1
- Ôn tập Tốt nghiệp THPT 2009-2010/Khảo sát hàm số và các bài toán liên quan/2
- Xem thêm liên kết đến trang này.
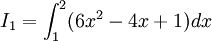
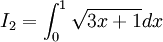
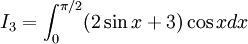
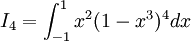
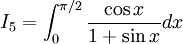
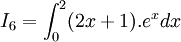
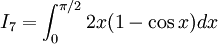
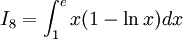
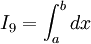
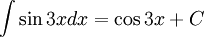
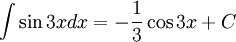
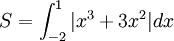
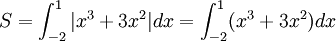 ,
vì
,
vì
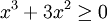 trên
[-2;
1].
trên
[-2;
1].
