Ôn tập Tốt nghiệp THPT 2009-2010/Khảo sát hàm số và các bài toán liên quan/5
Lý thuyết[sửa]
-
Cơ
sở:
Hoành
độ
giao
điểm
nếu
có
của
(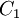 )
và
(
)
và
(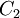 )
là
nghiệm
của
phương
trình
)
là
nghiệm
của
phương
trình
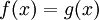
- Các bài toán:
+ Từ đồ thị ⇒ số giao điểm ⇒ số nghiệm
+ Từ số nghiệm của phương trình ⇒ số giao điểm
+ Ứng dụng cực trị ⇒ số nghiệm, số giao điểm với trục hoành.
Ví dụ[sửa]
Cho
hàm
số
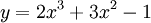 .
.
1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.
2)
Biện
luận
theo
m
số
nghiệm
thực
của
phương
trình
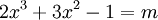 .
.
Tìm
m
để
đồ
thị
hàm
số
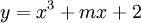 cắt
trục
hoành
tại
một
điểm
duy
nhất.
cắt
trục
hoành
tại
một
điểm
duy
nhất.
Cho
hàm
số
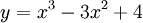 .
.
1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
2. Tìm toạ độ các giao điểm của đồ thị (C) và đường thẳng y = 4.
Cho
hàm
số
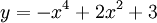 có
đồ
thị
(C).
có
đồ
thị
(C).
1. Khảo sát hàm số trên.
2.
Xác
định
m
để
phương
trình
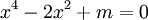 có
4
nghiệm
phân
biệt.
có
4
nghiệm
phân
biệt.
Bài tập tự luyện[sửa]
Cho
hàm
số
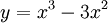
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho.
2.
Tìm
các
giá
trị
của
tham
số
m
để
phương
trình
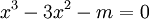 có
ba
nghiệm
phân
biệt.
có
ba
nghiệm
phân
biệt.
1.
Khảo
sát
và
vẽ
đồ
thị
(C)
của
hàm
số
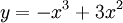 .
.
2.
Dựa
vào
đồ
thị
(C),
biện
luận
theo
m
số
nghiệm
của
phương
trình
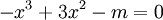 .
.
3. Tính diện tích hình phẳng giới hạn bởi (C) và trục hoành.
1.
Khảo
sát
và
vẽ
đồ
thị
(C)
của
hàm
số
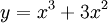 .
.
2. Tính diện tích hình phẳng giới hạn bởi đồ thị (C), trục hoành và các đường thẳng x = - 2, x = - 1.
Cho
hàm
số
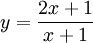 có
đồ
thị
(C)
có
đồ
thị
(C)
1) Khảo sát và vẽ đồ thị hàm số
2) Tính diện tích hình phẳng giới hạn bởi trục tung, trục hoành và đồ thị (C).
3) Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến đó đi qua điểm A(-1;3).
Cho
hàm
số
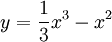 có
đồ
thị
(C).
có
đồ
thị
(C).
1) Khảo sát hàm số
2) Viết phương trình các tiếp tuyến của (C) đi qua điểm A(3; 0).
3) Tính thể tích của vật thể tròn xoay do hình phẳng giới hạn bởi (C) và các đường y = 0, x = 0, x = 3 quay quanh trục Ox.
Cho
hàm
số
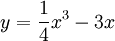 có
đồ
thị
(C).
có
đồ
thị
(C).
1) Khảo sát và vẽ đồ thị hàm số.
2)
Cho
điểm
M
thuộc
đồ
thị
(C)
có
hoành
độ
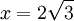 .
Viết
phương
trình
đường
thẳng
d
qua
M
và
là
tiếp
tuyến
của
(C).
.
Viết
phương
trình
đường
thẳng
d
qua
M
và
là
tiếp
tuyến
của
(C).
3) Tính diện tích hình phẳng giới hạn bởi (C) và tiếp tuyến của nó tại điểm M.
Cho
hàm
số
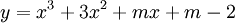 có
đồ
thị
có
đồ
thị
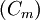 .
.
1) Khảo sát và vẽ đồ thị (C) của hàm số khi m = 3.
2) Gọi A là giao điểm của (C) và trục tung. Viết phương trình tiếp tuyến của (C) tại A. Tính diện tích hình phẳng giới hạn bởi (C) và tiếp tuyến trên.
3)
Tìm
giá
trị
của
m
để
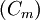 cắt
trục
hoành
tại
3
điểm
phân
biệt.
cắt
trục
hoành
tại
3
điểm
phân
biệt.
Cho
hàm
số
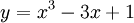 có
đồ
thị
(C).
có
đồ
thị
(C).
1) Khảo sát và vẽ đồ thị (C) của hàm số.
2) Tính diện tích hình phẳng giới hạn bởi đồ thị (C), trục hoành, trục tung và đường thẳng x = -1.
3) Đường thẳng d qua điểm uốn của (C) và có hệ số góc k. Biện luận theo k số giao điểm của (C) và đường thẳng d. Tìm tọa độ giao điểm đó khi k = 1.
Chủ đề khác[sửa]
- Khảo sát hàm số và các bài toán liên quan
- Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
- Hàm số, phương trình, bất phương trình mũ và lôgarit
- Hình học không gian tổng hợp
- Phương pháp tọa độ trong không gian
- Nguyên hàm, tích phân, ứng dụng
- Số phức
<comments
/>

