Phân bậc hoạt động
Trong hoạt động, kết quả rèn luyện được ở một mức nào đó có thể lại là tiền đề để tập luyện và đạt kết quả cao hơn. Điều này lại càng rõ ràng hơn đối với môn toán. Do đó trong hoạt động phải có phân bậc theo những mức độ khác nhau. Mức độ yêu cầu của hoạt động có thể là dài lâu: một mục, một chương, một kì, một năm,... hay cũng có thể là ngắn ngủi... Ở đây ta chỉ xét trong phạm vi ngắn là một tiết dạy.
Mục lục
Thế nào là phân bậc hoạt động[sửa]
Để điều khiển quá trình dạy học đạt kết quả cao ta phải xác định đúng mức độ, yêu cầu (mục tiêu) mà học sinh phải đạt được ở mỗi bước trung gian hay là ở mỗi bước cuối cùng của mỗi hoạt động. Đây chính là sự phân bậc hoạt động.
Mức độ yêu cầu của hoạt động có thể là dài lâu: một mục, một chương, một kì, một năm,... hay cũng có thể là ngắn ngủi... Ở đây ta chỉ xét trong phạm vi ngắn là một tiết dạy.
Trong phạm vi một tiết dạy thì việc xác định mức độ, yêu cầu (phân bậc) càng cụ thể, chi tiết, tránh được sự chung chung, mơ hồ thì chất lượng của hoạt động càng cao.
Những căn cứ để phân bậc hoạt động[sửa]
Sự phức tạp của đối tượng hoạt động[sửa]
Sự phức tạp của đối tượng hoạt động, tức là nội dung kiến cần truyền thụ, được thể hiện ở: số lượng các yếu tố toán học cần truyền thụ như biến số, tham số, điểm, đường thẳng, đoạn thẳng,... Ví dụ như:
Định lí về nhiều đường thẳng đồng quy bị cắt bởi nhiều đường thẳng song song, ta phân bậc theo số tia trong chùm đường thẳng và số đường thẳng song song.
So sánh hai nghiệm của phương trình bậc hai với một hay hai số thực, ta phân bậc theo so sánh với 1 số (3 trường hợp) và 2 số (6 trường hợp).
Mức độ khó, dễ của nội dung[sửa]
Ví dụ: Phương pháp giải các bất phương trình có chứa dấu căn thức có thể chia làm 3 mức độ:
-
Giải
bất
phương
trình:
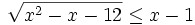
-
Giải
bất
phương
trình:
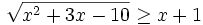
-
Giải
bất
phương
trình:
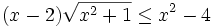
Yêu cầu về phát triển trí tuệ của học sinh[sửa]
- Tăng dần từ mức độ cụ thể đến trừu tượng trong quá trình học sinh nhận thức khái niệm.
- Tăng dần từ mức độ đặc biệt hóa đến khái quát hóa trong quá trình học sinh nhận thức định lí và tính chất.
Ví dụ: Sự nâng cao dần mức độ từ cụ thể đến trừu tượng hóa, khái quát hóa qua việc tính vận tốc tức thời của một chuyển động có thể chia làm 3 bậc:
- Tính V1 của chuyển động S = 200t - 5t2 tại thời điểm t = 3 giây.
- Tính V2 của chuyển động S = 200t - 5t2 tại thời điểm t bất kì.
- Tính V3 của chuyển động S(t) = f(t) tại thời điểm t tùy ý.
Yêu cầu về trình độ lĩnh hội của học sinh[sửa]
Tùy theo mức độ lĩnh hội (tính độc lập, độ thành thạo) của học sinh mà phân bậc hoạt động: tìm hiểu, tái hiện, vận dụng hay sáng tạo.
Ví dụ: Giải phương trình bậc hai có thể chia làm 3 mức độ:
- Giải theo công thức với phương trình có hệ số bằng số.
- Giải và biện luận phương trình có tham số.
- Biến đổi để đưa phương trình ban đầu về dạng bậc hai.
Lưu ý rằng, trong dạy học có thể phân bậc theo từng tiêu chuẩn như trên, nhưng nhiều khi ta phải phối hợp các tiêu chuẩn đó sao cho phù hợp với trình độ của học sinh và yêu cầu của bài dạy.
Ví dụ: Dạy bài "So sánh một số với các nghiệm của tam thức bậc hai"
Yêu cầu phải đạt:
- Học sinh phải tự rút ra được định lí đảo từ bảng tóm tắt về dấu tam thức và chứng minh được.
- Học sinh sơ bộ thấy được ý nghĩa và tác dụng của định lí này và hệ quả của nó: Chứng minh một phương trình bậc hai có nghiệm mà không cần xét biệt thức Δ và cũng không cần tìm ra nghiệm cụ thể, vì nhiều khi việc làm này gặp khó khăn.
- Có kĩ năng sơ bộ về cách tìm hai số α, β để đạt yêu cầu nhanh nhờ vào đặc điểm của phương trình.
Phân bậc hoạt động:
Bậc 1: Ôn tập kiến thức cũ - Tạo động cơ ban đầu - Đặt vấn đề.
Không giải phương trình, hãy chứng tỏ các phương trình sau đây có nghiệm:
- a) 3x2 - 4x - 5 = 0.
-
b)
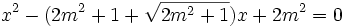 (m
là
tham
số)
(m
là
tham
số)
Bậc 2: Hình thành và chứng minh định lí - Phân tích, nhận xét, so sánh, dự đoán, lập mệnh đề đảo (tư duy thuận nghịch).
Từ bảng xét dấu tam thức bậc hai đã học hãy rút ra mệnh đề đảo và chứng minh, phát biểu định lí đảo.
Bậc 3: Hiểu và vận dụng ở mức độ thấp- Nhận dạng và thể hiện - Bước đầu khái quát hóa để rút kinh nghiệm về việc tìm số α.
- a) Cho biết α = 0, áp dụng định lí để chứng minh phương trình 2x2 - x - 1 = 0 có nghiệm.
- b) Tìm số α, áp dụng định lí, chứng minh các phương trình sau có nghiệm: -3x2 + 2x + 1 = 0 và 2x2 - 11x + 1 = 0.
- c) Vấn đề là tìm được số α thích hợp, tìm như thế nào?
Bậc 4: Vận dụng kinh nghiệm vừa có, áp dụng định lí ở mức độ cao hơn - Rèn luyện kĩ năng.
Vận dụng định lí, chứng minh rằng các phương trình sau đây có nghiệm:
- a) m2x2 - 2(m + 1)x - 4m2 + 4m + 3 = 0.
-
b)
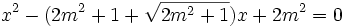 (m
là
tham
số)
(m
là
tham
số) - c) (x - a)(x - b) + (x - b)(x - c) + (x - c)(x - a)= 0 với a < b < c.
Bậc 5: Hiểu sâu định lí - Rèn luyện năng lực sáng tạo.
Nếu ta tìm được số α mà tích a.f(x) > 0 thì có thể kết luận điều gì?
Bậc 6: Hệ quả của định lí - Nhận xét để thấy sự thuận lợi của hai công cụ vừa có - Hệ thống các công cụ để chứng minh một tam thức bậc hai có nghiệm:
- a) Tiếp xúc ban đầu:
- Nếu ta có α sao cho a.f(x) < 0 và β sao cho a.f(x) > 0. Hãy xét dấu của tích a.f(α).a.f(β) và kết luận. Hãy rút gọn tích trên! Nhận xét ưu nhược điểm của định lí và hệ quả khi áp dụng.
- b) Áp dụng: m(x - 3)(x - 5) + x2 - 15 = 0.
- c) Hãy kể ra những công cụ mà ta đã có để chứng minh một tam thức (phương trình) bậc hai có nghiệm, kinh nghiệm khi vận dụng.
Tác dụng của hoạt động hóa trong việc điều khiển quá trình dạy học[sửa]
Nhờ việc tổ chức hoạt động, đặc biệt là phân bậc hoạt động trong dạy học mà giáo viên có thể điều khiển quá trình dạy học trên lớp tốt hơn, thể hiện ở chỗ:
- Xác định mục đích, yêu cầu giờ dạy được cụ thể hóa và sát đúng hơn.
- Xác định phương pháp dạy học thích hợp.
- Trên cơ sở phân bậc mà có thể tuần tự nâng cao yêu cầu hoặc hạ thấp yêu cầu khi cần thiết.
- Xác định được mức độ khi tiến hành dạy học phân hóa nội tại.
Tài liệu tham khảo[sửa]
- Giáo trình PPDH môn Toán, phần đại cương, Trần Khánh Hưng, Nhà xuất bản giáo dục, 1997, trang 65
- Giáo trình PPDH môn Toán, phần đại cương, Nguyễn Bá Kim, Vũ Dương Thụy, Nhà xuất bản giáo dục, 2000, 94. (khai thác chưa hết)


