Hướng đích và gợi động cơ

Dạy học là tác động lên đối tượng học sinh (con người) nên để việc thực hiện các hoạt động có kết quả, họ cần phải hoạt động tích cực, tự giác. Do đó cần chỉ (bằng lời nói, chữ viết,... ) cho hs biết/hiểu mục đích phải đến và tạo cho hs sự say mê, hứng thú, tự thấy mình có nhu cầu phải khám phá và giải quyết một mâu thuẫn nào đó nảy sinh.

Hướng đích[sửa]

Đặt mục đích cuối cùng hay từng bước cho học sinh thấy để chủ động hướng hoạt động của mình vào đó. Muốn vậy người giáo viên cần nắm chắc nội dung, các văn bản hướng dẫn và giải thích chương trình, sách giáo khoa và các tài liệu tham khảo,... để xác định được mục đích cần đạt mà không sa và các chi tiết "kĩ thuật" trong khi chứng minh hay giải bài toán. Từ đó làm cho học sinh ý thức được con đường mình phải đi tới đích, đi theo những bước cụ thể nào, với "công cụ" gì, tránh được việc làm cầu may được chăng hay chớ, mà phải tìm ra con đường đi thích hợp.

Ví dụ 1: Tìm công thức tổng quát để giải phương trình bậc hai:

ax² + bx + c = 0 với a ≠ 0 (lớp 9)

Bước 1:

Hãy giải các phương trình:

x²	= 4	(1)
4x²	= 9	(2)
x² + 3x	= 0	(3)
(x - 3)²	= 1	(4)

Ta đã biết cách giải các phương trình bậc hai với hệ số bằng số. Hãy tìm cách (một công thức tổng quát) để giải phương trình ax² + bx + c = 0 với hệ số bằng chữ?

Bước 2:

Hãy chỉ ra các hệ số a, b, c trong các phương trình 1, 2, 3 và 4 ở trên. Hãy biến đổi phương trình 4 về dạng tổng quát!?

Đó là x² - 6x + 8 = 0 (4'), phương trình 4 ta đã biết giải dễ dàng, nhưng (4') ta chưa có cách giải. Hãy biến đổi để đưa (4') về dạng (4)?

Tương tự, hãy đưa phương trình sau về dạng (4): 3x² + 2x - 5 = 0. Hệ số a = 3, làm thế nào đưa về dạng (4')?

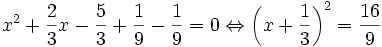x^{2}+{\frac 23}x-{\frac 53}+{\frac 19}-{\frac 19}=0\Leftrightarrow \left(x+{\frac 13}\right)^{2}={\frac {16}9}

(5)

Nhận xét hai vế của (5)?

Đưa dạng tổng quát về dạng (x + A)² = B, trong đó A và B chỉ chứa các hệ số a, b, c!

Ví dụ 2: Chứng minh định lí: "Nếu hai mặt phẳng cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng (nếu có) sẽ vuông góc với mặt phẳng ấy". (Hình học 11)

Bước 1:

Tìm hiểu định lí:

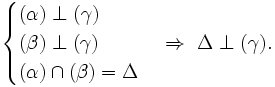
{\begin{cases}(\alpha )\perp (\gamma )\\(\beta )\perp (\gamma )\\(\alpha )\cap (\beta )=\Delta \end{cases}}\Rightarrow \ \Delta \perp (\gamma ).

Nhắc lại mục đích: Chứng minh 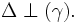$\Delta \perp (\gamma ).$ Để đạt được mục đích này ta đi theo hướng nào?

a) Chứng minh Δ vuông góc với 2 đường thẳng giao nhau nào đó nằm trong mp(γ).

b) Tìm một đường thẳng m nào đó vuông góc với mp(γ) và ta chứng minh Δ // m.

Xác định hướng đi: Căn cứ vào giả thiết ta chọn hướng b.

Bước 2: Phân tích giả thiết, tìm sự liên quan theo hướng b.

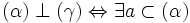(\alpha )\perp (\gamma )\Leftrightarrow \exists a\subset (\alpha )

và

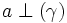
a\perp (\gamma )

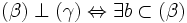(\beta )\perp (\gamma )\Leftrightarrow \exists b\subset (\beta )

và

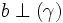
b\perp (\gamma )

Hãy dựa vào các định lí đã học tìm mối liên tương quan giữa ba đường thẳng a, b và Δ.

Gợi động cơ[sửa]

Tạo cho hs một động cơ, một ham muốn tìm ra con đường đi tới đích. Từ đó khêu gợi trí tò mò khoa học, sự hứng thú khám phá cái mới. Đây chính là một biện pháp quan trọng để phát huy tính tự giác, chủ động trong học tập của hs.^[1] Sau đây là một số biện pháp thực hiện:

Giải quyết mâu thuẫn[sửa]

Đáp ứng nhu cầu muốn giải quyết một mâu thuẫn, xóa bỏ một hạn chế nảy sinh từ thực tế hay từ nội bộ toán học.

Ví dụ 1: Mở rộng tập số tự nhiên 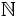${\mathbb {N}}$ thành tập số nguyên 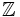${\mathbb {Z}}$ để phép trừ luôn thực hiện được. (từ nội bộ toán học)

Ví dụ 2: Tìm cực trị của một hàm số bằng đạo hàm bậc hai khi vệc xét dấu đạo hàm bậc một gặp khó khăn như hàm số:

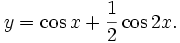
y=\cos x+{\frac 12}\cos 2x.

Xem thêm: Tạo tình huống có vấn đề trong dạy học môn Toán/Bài toán chưa có thuật giải

Hướng tới sự hoàn chỉnh và hệ thống[sửa]

Ví dụ 1: Trong tam giác vuông tại A ta có a² = b² + c², còn khi A ≠ 90° thì a² =?

Ví dụ 2: Ta đã biết cách giải phương trình bậc hai khuyết, còn phương trình bậc hai đầy đủ ax² + bx + c = 0 thì sao?

Xem thêm: Tạo tình huống có vấn đề trong dạy học môn Toán/Từ cũ đến mới

Lật ngược vấn đề[sửa]

Ví dụ 1: Nếu tứ giác ABCD nội tiếp trong một đường tròn thì A + C = B + D = 180°, còn ngược lại?

Ví dụ 2: Định lí đảo dấu tam thức bậc hai

Xem thêm: Tạo tình huống có vấn đề trong dạy học môn Toán/Lật ngược vấn đề

Xét trường hợp tương tự[sửa]

Ví dụ 1: Trong mặt phẳng ta đã xét hai đường thẳng cùng vuông góc với một đường thẳng, trong không gian hãy xét tương tự: hai mặt phẳng cùng vuông góc với một đường thẳng, hai đường thẳng cùng vuông góc với một mặt phẳng, hai mặt phẳng cùng vuông góc với một mặt phẳng, hai, ba đường thẳng cùng vuông góc với một đường thẳng.

Ví dụ 2: Ta đã biết cách tính tổng:

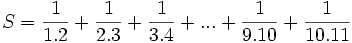
S={\frac {1}{1.2}}+{\frac {1}{2.3}}+{\frac {1}{3.4}}+...+{\frac {1}{9.10}}+{\frac {1}{10.11}}

Hãy tính:

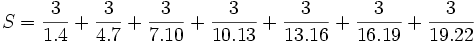
S={\frac {3}{1.4}}+{\frac {3}{4.7}}+{\frac {3}{7.10}}+{\frac {3}{10.13}}+{\frac {3}{13.16}}+{\frac {3}{16.19}}+{\frac {3}{19.22}}

Xem thêm: Tạo tình huống có vấn đề trong dạy học môn Toán/Tương tự hóa

Khái quát hóa[sửa]

Ví dụ 1: Ta đã biết tổng các góc trong của một tam giác là 180° còn tứ giác lồi, đa giác lồi?

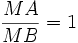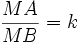Ví dụ 2: Với 2 điểm A, B cho trước ta biết tập hợp các điểm M sao cho MA = MB (hay ${\frac {MA}{MB}}=1$ ) là đường trung trực của đoạn AB. Còn tập hợp các điểm M sao cho ${\frac {MA}{MB}}=k$ (k > 0, k ≠ 1) là gì?

Xem thêm: Tạo tình huống có vấn đề trong dạy học môn Toán/Khái quát hóa

Quy lạ về quen[sửa]

Ví dụ 1: Chứng minh các tính chất của hàm số logarit nhờ hàm số mũ.

Ví dụ 2: Tìm cách giải phương trình asin x + bcos x = c nhờ đưa về phương trình sin x = a, tan x = a,...

Tìm mối liên hệ, phụ thuộc giữa các đại lượng, các yếu tố[sửa]

Ví dụ 1: Vị trí giữa hai đường tròn phụ thuộc vào những yếu tố nào?

Ví dụ 2: Mối liên hệ giữa các hệ số a, b, c với vị trí, dáng điệu của đồ thị hàm số y = ax² + bx + c.

Xem thêm: Tạo tình huống có vấn đề trong dạy học môn Toán/Tư duy hàm

Xem thêm[sửa]

Tài liệu tham khảo[sửa]

Giáo trình PPDH môn Toán, phần đại cương, Trần Khánh Hưng, Nhà xuất bản giáo dục, 1998, trang 58
Giáo trình PPDH môn Toán, phần đại cương, Nguyễn Bá Kim, Vũ Dương Thụy, Nhà xuất bản giáo dục, 2000, 79. (khai thác chưa hết)

↑ Các phương pháp không những làm cho việc dạy học có hiệu quả hơn mà còn hấp dẫn hơn và có thể trở thành một biện pháp để giải quyết vấn đề hấp dẫn trong giáo dục, vấn đề bỏ học,... (Trích Báo cáo tổng kết giai đoạn chuẩn đoán tình hình giáo dục và đào tạo, Hà Nội 2/1992, VIE, 89/002.)

« Mới nhất
‹ Mới hơn
Cũ hơn ›

Liên kết đến đây

[1] Các phương pháp không những làm cho việc dạy học có hiệu quả hơn mà còn hấp dẫn hơn và có thể trở thành một biện pháp để giải quyết vấn đề hấp dẫn trong giáo dục, vấn đề bỏ học,... (Trích Báo cáo tổng kết giai đoạn chuẩn đoán tình hình giáo dục và đào tạo, Hà Nội 2/1992, VIE, 89/002.)

[1]

Hướng đích và gợi động cơ

Mục lục

Hướng đích[sửa]