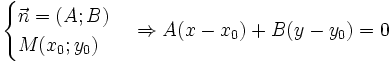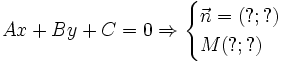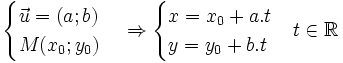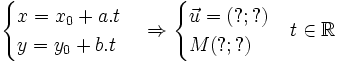Tạo tình huống có vấn đề trong dạy học môn Toán/Lật ngược vấn đề
Đường
tròn
tâm
I(a;
b),
bán
kính
R
có
phương
trình
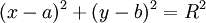 .
Khai
triển
phương
trình
này
ta
được
phương
trình
dạng:
.
Khai
triển
phương
trình
này
ta
được
phương
trình
dạng:
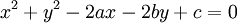 với
với
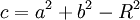 .
Vấn
đề
ngược
lại
là
với
a,
b,
c
tùy
ý
thì
phương
trình
.
Vấn
đề
ngược
lại
là
với
a,
b,
c
tùy
ý
thì
phương
trình
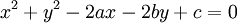 có
là
phương
trình
của
một
đường
tròn
không,
và
nếu
có
thì
đường
tròn
đó
có
tâm
và
bán
kính
như
thế
nào?[1]
có
là
phương
trình
của
một
đường
tròn
không,
và
nếu
có
thì
đường
tròn
đó
có
tâm
và
bán
kính
như
thế
nào?[1]
Nếu một tứ giác nội tiếp trong một đường tròn thì tổng hai góc đối diện luôn bằng 180°, còn ngược lại? Một tứ giác có tổng hai góc đối diện bằng 180° thì tứ giác đó có nội tiếp?
Định lí đảo dấu tam thức bậc hai
Hình thành định lí đảo của định lí Pitago
Đặt vấn đề: “Trong tam giác vuông bình phương cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông”.
Vậy ngược lại “Nếu một tam giác có bình phương một cạnh bằng tổng các bình phương của hai cạnh còn lại thì tam giác đó có là tam giác vuông không?”
Hình thành tỉ lệ thức
Từ
tỉ
lệ
thức
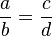 ta
suy
ra
đẳng
thức
a.d
=
b.c.
ta
suy
ra
đẳng
thức
a.d
=
b.c.
Vậy từ đẳng thức a.d = b.c ta có thể suy ra tỉ lệ thức nào?
Hình thành phép trừ
Cho hai số tự nhiên a và b ta có thể tìm được tổng của chúng. Ngược lại, biết một số tự nhiên c, ta có thể tìm được hai số a và b sao cho a + b = c không?
Ví dụ: tìm hai số a và b sao cho a + b = 3.
-
- Trường hợp đặc biệt, c = 0, ta có khái niệm số đối
Cho
hai
vector
 ,
ta
có
vẽ
được
vector
tổng
của
chúng.
Ngược
lại,
cho
trước
một
vector
,
ta
có
vẽ
được
vector
tổng
của
chúng.
Ngược
lại,
cho
trước
một
vector
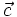 ,
ta
có
thể
vẽ
được
hai
vector
,
ta
có
thể
vẽ
được
hai
vector
 sao
cho
sao
cho
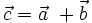 không?
không?
-
Có
hai
khả
năng:
 và
và
 cùng
phương;
cùng
phương;
 và
và
 không
cùng
phương
không
cùng
phương - Giáo viên tổ chức sao cho học sinh gặp cả hai tình huống
- Qua đó, giới thiệu trường hợp hai được gọi là "phân tích một vectơ thành hai vectơ không cùng phương".
-
-
Trường
hợp
đặc
biệt,
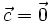 ,
ta
có
khái
niệm
vectơ
đối
,
ta
có
khái
niệm
vectơ
đối
-
Trường
hợp
đặc
biệt,
Ta
đã
biết:
Nếu
có
số
thực
k
để
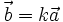 thì
thì
 và
và
 cùng
phương.
Ngược
lại,
nếu
cùng
phương.
Ngược
lại,
nếu
 và
và
 cùng
phương
liệu
có
tồn
tại
một
số
k
để
cùng
phương
liệu
có
tồn
tại
một
số
k
để
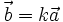 ?
?
Khi
biết
tọa
độ
của
một
vectơ
pháp
tuyến
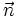 và
tọa
độ
một
điểm
M
của
đường
thẳng
Δ
ta
viết
được
phương
trình
tổng
quát
của
nó.
và
tọa
độ
một
điểm
M
của
đường
thẳng
Δ
ta
viết
được
phương
trình
tổng
quát
của
nó.
Ngược lại, khi biết phương trình tổng quát của một đường thẳng ta có thể tìm được tọa độ của một vectơ pháp tuyến và tọa độ một điểm của nó không?
Khi
biết
tọa
độ
của
một
vectơ
chỉ
phương
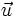 và
tọa
độ
một
điểm
M
của
đường
thẳng
Δ
ta
viết
được
phương
trình
tham
số
của
nó.
và
tọa
độ
một
điểm
M
của
đường
thẳng
Δ
ta
viết
được
phương
trình
tham
số
của
nó.
Ngược lại, khi biết phương trình tham số của một đường thẳng ta có thể tìm được tọa độ của một vectơ chỉ phương và tọa độ một điểm của nó không?
Đồ thị của hàm số bậc nhất y = ax + b (a ≠ 0) là một đường thẳng. Ngược lại, mỗi đường thẳng có là đồ thị của một hàm số bậc nhất nào đó?
Cho
một
bất
phương
trình
bậc
hai,
ta
tìm
được
tập
nghiệm
của
nó.
Bây
giờ
ngược
lại,
cho
tập
hợp
![\left(-\infty ;{\frac 12}\right]\cup [3;+\infty )](https://tusach.thuvienkhoahoc.com/images/math/a/2/a/a2a4c0b7a3f557e70424d85173ec1a63.png) ,
hãy
thành
lập
một
bất
phương
trình
bậc
hai
nhận
tập
hợp
đó
làm
tập
nghiệm.[2]
,
hãy
thành
lập
một
bất
phương
trình
bậc
hai
nhận
tập
hợp
đó
làm
tập
nghiệm.[2]
Chú thích[sửa]
- ↑ Tham khảo: SGK Hình học nâng cao 10, NXB Giáo dục 2006, trang 91
- ↑ Tài liệu Bồi dưỡng thường xuyên giáo viên Trung học phổ thông chu kì III (2004-2007) Toán học, Bùi Văn Nghị - Vương Dương Minh – Nguyễn Anh Tuấn, NXB Đại học Sư phạm, 2005, trang 134