Dạy học phát hiện và giải quyết vấn đề trong môn Toán học
Trước hết, ta hãy so sánh hai cách dạy học thông qua ví dụ sau:
- Định lí về tổng các góc trong của một tứ giác [1]
Cách 1: Giáo viên nêu nhiệm vụ chứng minh định lí: "Tổng các góc trong của một tứ giác bằng 360° hay 4v" [2]. Sau đó giáo viên trình bày chứng minh.
Cách 2: Cách này thể hiện qua đoạn hội thoại dựa vào các câu hỏi sau đây của giáo viên:
- H1: Một tam giác bất kì, tổng các góc trong bằng 2v. Bây giờ cho một tứ giác bất kì, chẳng hạn ABCD, liệu ta có thể nói gì về tổng các góc trong của nó? Liệu tổng các góc trong của nó có phải là một hằng số tương tự như trường hợp tam giác hay không?
- H2: Ta đã biết chứng minh định lí về tổng các góc trong của một tam giác. Liệu có thể đưa được trường hợp tứ giác về trường hợp tam giác hay không? Làm thế nào để xuất hiện những tam giác?[3]
- H3: Bây giờ hãy tính tổng các góc trong của tứ giác ABCD.
- H4: Hãy phát biểu kết quả vừa tìm được.
Trong cách thứ nhất, thầy là chính, trò là thụ động, thầy nói, trò nghe và chỉ làm theo lệnh của thầy.
Trong cách thứ hai, thầy đã tổ chức cho trò học tập trong hoạt động và bằng hoạt động do thầy tạo ra một tình huống hấp dẫn gợi sự tìm hiểu của học sinh, gợi ra vướng mắc mà họ chưa giải đáp ngay được, nhưng có liên hệ với tri thức đã biết, khiến họ thấy có triển vọng tự giải đáp được nếu tích cực suy nghĩ. Đó là cách dạy học phát hiện và giải quyết vấn đề.
1. Những khái niệm cơ bản[sửa]
1.1. Vấn đề[sửa]
- Hệ thống được hiểu là một tập hợp những phần tử cùng với những quan hệ giữa những phần tử của tập hợp đó.
- Một tình huống[4] được hiểu là một hệ thống phức tạp gồm chủ thể và khách thể, trong đó chủ thể có thể là người, còn khách thể lại là một hệ thống nào đó.
- Nếu trong một tình huống, chủ thể còn chưa biết ít nhất một phần tử của khách thể thì tình huống này được gọi là một tình huống bài toán đối với chủ thể
- Trong một tình huống bài toán, nếu được chủ thể đặt ra mục tiêu tìm phần tử chưa biết nào đó dựa vào một số những phần tử cho trước ở trong khách thể thì ta có một bài toán.
- Một bài toán được gọi là vấn đề nếu chủ thể chưa biết một thuật giải nào có thể áp dụng để tìm ra phần tử chưa biết của bài toán.[5]
1.2. Tình huống có vấn đề và tình huống gợi vấn đề[sửa]
Tình huống có vấn đề là tình huống trong đó tồn tại một vấn đề.
Tình huống gợi vấn đề là tình huống thỏa mãn ba điều kiện sau:
a) Tồn tại một vấn đề
b) Gợi nhu cầu nhận thức
Nếu tình huống có vấn đề, nhưng vì một lí do nào đó mà học sinh không có hứng thú tìm hiểu, suy nghĩ để tìm cách giải quyết (chẳng hạn vì họ cảm thấy chẳng có ích gì cho mình, hay vì quá mệt mỏi,...) thì đó cũng không phải là tình huống gợi vấn đề. Điều quan trọng là tình huống phải gợi nhu cầu nhận thức, chẳng hạn làm bộ lộ sự khuyến khuyết về kiến thức và kĩ năng của học sinh để họ thấy cần thiết phải bổ sung, điều chỉnh, hoàn thiện tri thức, kĩ năng bằng cách tham gia giải quyết vấn đề nảy sinh.
c) Gây niềm tin ở khả năng bản thân
Nếu tình huống có vấn đề rất hấp dẫn, lôi cuốn học sinh có nhu cầu giải quyết, nhưng nếu họ cảm thấy vấn đề vượt quá so với khả năng của mình thì họ cũng không còn hứng thú, không sẵn sàng giải quyết vấn đề. Tình huống gợi vấn đề phải bộ lộ mối quan hệ (có thể khá mờ nhạt) giữa vấn đề cần giải quyết và vốn kiến thức sẵn có của chủ thể, và tạo ra ở họ niềm tin rằng nếu tích cực suy nghĩ thì sẽ thấy rõ hơn mối quan hệ này và có nhiều khả năng tìm ra cách giải quyết.
Tóm lại, tình huống gợi vấn đề là tình huống gợi ra cho học sinh những khó khăn về lí luận hay thực tiễn mà họ thấy cần thiết và có khả năng vượt qua, nhưng không phải ngay tức thì nhờ vào một quy tắc có tính thuật toán mà phải trải qua một quá trình tích cực suy nghĩ, hoạt động để đồng hóa nó hay điều chỉnh hệ thống kiến thức sẵn có nhằm thích nghi với điều kiện hành động mới.
Các điều kiện b và c ở trên cho phép phân biệt tình huống gợi vấn đề với tình huống có vấn đề. Một tình huống có vấn đề chỉ cần thỏa mãn điều kiện a.
Việc tạo ra một tình huống gợi vấn đề không phải là dễ dàng. Quả thực, làm thế nào để vấn đề đặt ra đảm bảo đủ hai điều kiện: gợi nhu cầu nhận thức và gây niềm tin ở khả năng? Đó là một câu hỏi lớn rất cần thiết được nghiên cứu trả lời. Chính vì vậy, trong thực tế dạy học ở trường phổ thông, giáo viên thường chỉ mới dừng lại ở mức độ tạo ra được tình huống có vấn đề, chứ chưa phải là tình huống gợi vấn đề. Tuy nhiên, ngay cả khi chỉ tạo được tình huống có vấn đề, thì việc áp dụng đúng như các bước đã nêu của dạy học đặt và giải quyết vấn đề cũng mang lại hiệu quả cao hơn nhiều so với phương pháp dạy học truyền thống.
1.2.1. Ví dụ về tình huống có vấn đề[sửa]
Trong
giờ
học
về
phương
trình
lượng
giác
cơ
bản,
giáo
viên
thực
hiện
pha
hỏi
bài
cũ
bằng
cách
yêu
cầu
học
sinh
giải
bài
toán:
"Cho
x
các
giá
trị
lần
lượt
là
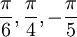 .
Tính
.
Tính
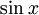 ".
Một
trong
các
mục
đích
chủ
yếu
là
đi
thẳng
tới
khẳng
định
rằng
nếu
cho
trước
một
giá
trị
bất
kì
của
x,
thì
luôn
tìm
được
giá
trị
(có
thể
gần
đúng)
của
".
Một
trong
các
mục
đích
chủ
yếu
là
đi
thẳng
tới
khẳng
định
rằng
nếu
cho
trước
một
giá
trị
bất
kì
của
x,
thì
luôn
tìm
được
giá
trị
(có
thể
gần
đúng)
của
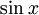 nhờ
vào
bảng
giá
trị
lượng
giác
của
các
góc
đặc
biệt,
máy
tính
bỏ
túi,
hay
đường
tròn
lượng
giác.
nhờ
vào
bảng
giá
trị
lượng
giác
của
các
góc
đặc
biệt,
máy
tính
bỏ
túi,
hay
đường
tròn
lượng
giác.
Từ đó, giáo viên đặt ra vấn đề cần giải quyết:
Ngược
lại,
nếu
cho
trước
một
giá
trị
bất
kì
của
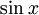 ,
chẳng
hạng
,
chẳng
hạng
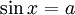 với
a
là
hằng
số,
thì
liệu
có
tồn
tại
hay
không
giá
trị
x
thỏa
mãn
với
a
là
hằng
số,
thì
liệu
có
tồn
tại
hay
không
giá
trị
x
thỏa
mãn
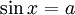 ?
Nếu
có
thì
có
bao
nhiêu
giá
trị
x?
Xác
định
chúng
như
thế
nào?
Nói
cách
khác,
giải
phương
trình
?
Nếu
có
thì
có
bao
nhiêu
giá
trị
x?
Xác
định
chúng
như
thế
nào?
Nói
cách
khác,
giải
phương
trình
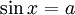 ra
sao?
ra
sao?
Tình
huống
trên
là
một
tình
huống
có
vấn
đề,
vì
tồn
tại
trong
đó
một
vấn
đề
mà
cho
đến
thời
điểm
đó
học
sinh
chưa
có
một
phương
pháp
tổng
quát
nào
để
giải
phương
trình
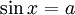 .
Tuy
nhiên,
nó
có
thể
chưa
phải
là
tình
huống
gợi
vấn
đề
vì
tình
huống
đặt
ra
như
vậy
chưa
đảm
bảo
chắc
chắn
tạo
ra
ở
học
sinh
sự
hứng
thú
và
nhu
cầu
muốn
tiến
hành
giải
quyết
vấn
đề.
.
Tuy
nhiên,
nó
có
thể
chưa
phải
là
tình
huống
gợi
vấn
đề
vì
tình
huống
đặt
ra
như
vậy
chưa
đảm
bảo
chắc
chắn
tạo
ra
ở
học
sinh
sự
hứng
thú
và
nhu
cầu
muốn
tiến
hành
giải
quyết
vấn
đề.
1.2.2. Ví dụ về tình huống gợi vấn đề[sửa]
Ví
dụ
1.
Giả
sử
đối
với
học
sinh
lớp
1
chưa
được
học
phép
trừ
nhưng
đã
làm
quen
với
một
số
bài
tập
về
phép
cộng
số
tự
nhiên,
giáo
viên
yêu
cầu
tìm
một
số
thích
hợp
điền
vào
chỗ
dấu ?
sao
cho
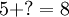 .
.
Ở đây, tồn tại vấn đề vì khi chưa học phép trừ thì học sinh chưa biết thuật giải để trực tiếp giải bài toán đó. Vấn đề này gợi nhu cầu nhận thức và gây được cho học sinh niềm tìn ở khả năng huy động tri thức, kĩ năng của mình, bởi vì dù sao bài tập trên cũng liên quan đến phép cộng là một tri thức mà học sinh đã biết; học sinh nghĩ rằng có thể tích cực suy nghĩ về phép cộng, vận dụng phép cộng thì có triển vọng giải được bài toán này. Như vậy, tình huống trên thỏa mãn các điều kiện của một tình huống gợi vấn đề.
Kinh nghiệm thực tế cho thấy rằng, với những suy nghĩ dựa trên phép cộng, vận dụng phép cộng, nhiều học sinh đã tìm ra lời giải bài tập trên một cách không khó khăn theo cách sau:
- 5 + 1 = 6
- 5 + 2 = 7
- 5 + 3 = 8
Đương nhiên, ở trình độ lớp 1, trong trường hợp này, người ta không yêu cầu lí giải tính duy nhất của đáp số.
Ví dụ 2. Bài toán được đặt ra cho học sinh của một lớp 8, Cộng hòa Pháp trong tình huống có thể mô tả như sau:
Học sinh làm việc theo nhóm. Mỗi nhóm khoảng 4 học sinh.
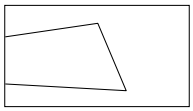
Giáo viên phát cho mỗi nhóm một bản photo hình vẽ trên giấy A4 cảu một tam giác bị cắt đi một mảnh có chứa một đỉnh, mà ta gọi là tam giác cụt (hình dưới đây), một số dụng cụ và vật liệu như: 2 thước đo độ, 2 thước kẻ, 2 eke, 2 compa, 4 bút bi, 1 máy tính chỉ cho phép thực hiện 4 phép toán Cộng, trừ, nhân, chia và nhiều tờ giấy A4 không trong suốt.
Giáo viên thông báo nhiệm vụ:
Bình luận: Tình huống này thỏa mãn ba điều kiện của tình huống gợi vấn đề
- Tồn tại một vấn đề: Quả thực, cho đến thời điểm này học sinh chưa cho một phương pháp có tính thuật toán nào để tính chu vi các tam giác cụt như vậy.
-
Bài
toán
tạo
ra
ở
học
sinh
sự
tò
mò,
hứng
thú
và
nhu
cầu
giải
quyết
vấn
đề
vì
ba
lí
do
chủ
yếu
sau:
- Bài toán khá khác lạ so với những bài toán tính chu vi mà học sinh thường gặp trong lớp. Nó thể hiện một sự độc đáo và thú vị.
- Nó được đặt trong tình huống phải thi đua giữa các nhóm để tạo ra một bản hướng dẫn đại diện cho lớp.
- Bản hướng dẫn sẽ được sử dụng bởi học sinh lớp khác. Điều này ảnh hưởng đến uy tín và danh dự của lớp.
- Dù là khác lạ, nhưng thoạt tiên, học sinh không cảm thấy quá khó phải bó tay, mà họ có thể tính đến nhiều phương án giải quyết khác nhau như: tìm phần bị thiếu bằng cách kéo dài hai cạnh bị cụt lên các tờ giấy khác hay trên mặt bàn, bằng gấp giấy hay bằng cách dùng phép đối xứng trục,... Chỉ đến khi hiểu rõ các rằng buộc của tình huống họ mới có thể nhận ra tính không hiệu quả cảu các cách giải quyết này. Ta nói, tồn tại các chiến lược cơ sở cho phép học sinh đưa ra những giải pháp đáp ban đầu. Việc nhận ra khiếm khuyết của chiến lược cơ sở sẽ buộc học sinh phải điều chỉnh phương thức giải quyết.
Chính sự tồn tại chiến lược cơ sở, cùng với cảm giác quen thuộc về bài toán tính chu vi tam giá là một trong các nhân tố góp phần tạo ra ở học sinh niềm tin vào khả năng giải quyết được vấn đề đặt ra.
2. Dạy học phát hiện và giải quyết vấn đề[sửa]
Một trong những mục đích cốt yếu của hình thức dạy học này là giúp học sinh phát triển các khả năng: khả năng phát hiện và trình bày vấn đề, khả năng tìm kiếm cách giải quyết vấn đề, khả năng tổ chức quá trình giải quyết vấn đề, khả năng kiểm tra đánh giá kết quả và phương pháp tiến hành giải quyết vấn đề, ... Nói cách khác, nó cũng cung cấp cho học sinh những tri thức phương pháp.[6]
2.1. Các bước chủ yếu[sửa]
Bước 1: Tạo tình huống gợi vấn đề [7]
Bước 2: Trình bày vấn đề và đặt mục tiêu giải quyết [8]
Bước 3: Giải quyết vấn đề
a) Tìm giải pháp[9]
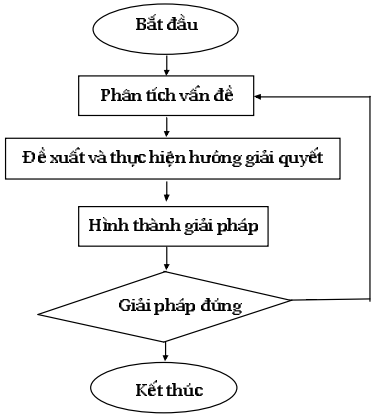
Tìm cách giải quyết vấn đề, thường được thực hiện theo sơ đồ sau:
Giải thích sơ đồ
- Phân tích vấn đề: làm rõ mối liên hệ giữa cái đã biết và cái cần tìm (dựa vào những tri thức đã học, liên tưởng tới kiến thức thích hợp)
- Hướng dẫn HS tìm chiến lược giải quyết vấn đề thông qua đề xuất và thực hiện hướng giải quyết vấn đề. Cần thu thập, tổ chức dữ liệu, huy động tri thức;[10] sử dụng những phương pháp, kĩ thuật nhận thức, tìm đoán suy luận như hướng đích, quy lạ về quen, đặc biệt hóa, chuyển qua những trường hợp suy biến, tương tự hóa, khái quát hóa, xem xét những mối liên hệ phụ thuộc, suy xuôi, suy ngược tiến, suy ngược lùi,... Phương hướng đề xuất có thể được điều chỉnh khi cần thiết. Kết quả của việc đề xuất và thực hiện hướng giải quyết vấn đề là hình thành được một giải pháp.
- Kiểm tra tính đúng đắn của giải pháp: Nếu giải pháp đúng thì kết thúc ngay, nếu không đúng thì lặp lại từ khâu phân tích vấn đề cho đến khi tìm được giải pháp đúng.
- Chọn giải pháp thích hợp: Sau khi đã tìm ra một giải pháp, có thể tiếp tục tìm thêm những giải pháp khác, so sánh chúng với nhau để tìm ra giải pháp hợp lí nhất.[11]
b) Trình bày giải pháp[12]
HS trình bày lại toàn bộ từ việc phát biểu vấn đề tới giải pháp. Nếu vấn đề là một đề bài cho sẵn thì có thể không cần phát biểu lại vấn đề.
Bước 4: Rút ra kết luận[13]
- Thể chế hóa kiến thức cần lĩnh hội[17]
Bước 5: Vận dụng kiến thức mới để giải quyết những nhiệm vụ đặt ra tiếp theo[18]
- Tìm hiểu những khả năng ứng dụng kết quả[19]
- Đề xuất những vấn đề mới có liên quan nhờ xét tương tự, khái quát hóa, lật ngược vấn đề,... và giải quyết nếu có thể.[20]
2.2. Khái niệm thể chế hoá và sự khác biệt giữa kiến thức và tri thức[sửa]
Khi một vấn đề đặt ra đã được giải quyết, có thể có một số kiến thức mới nảy sinh từ kết quả đạt được và rất có lợi để sử dụng về sau. Tuy nhiên, nếu ta chỉ dừng lại ở lời giải đã đạt được, thì những kiến thức bổ ích này cũng chỉ tồn tại dưới dạng kiến thức của cá nhân mỗi học sinh, như là kinh nghiệm của mỗi người rút ra từ hoạt động giải quyết vấn đề đã cho. Do đó, chúng không giống nhau ở mọi học sinh, và có thể việc sử dụng lại sau này là không hợp pháp.
Nhiệm vụ của giáo viên là biến các kiến thức cá nhân đó thành kiến thức chung (hay tri thức) có thể sử dụng về sau và sử dụng được một cách hợp pháp bởi mọi học sinh, bằng cách nêu lên và thông báo kiến thức này một cách tường minh dưới dạng một định lí, một công thức hay một quy tắc, phương pháp, ... Khi đó, ta nói giáo viên đã thực hiện pha thể chế hoá. Nói cách khác, thể chế hoá là hành động biến một kiến thức có tính cá nhân thành một kiến thức có tính xã hội (hay một tri thức)
Ví dụ: Sau khi tổ chức cho học sinh giải quyết xong các bài toán sau đây, mà định hướng khởi đầu là hạ bậc các biểu thức lượng giác bậc cao:
thì một tri thức phương pháp rất có ích có thể được rút ra là: "Khi giải các phương trình lượng giác phức tạp, nếu phương trình chứa các biểu thức lượng giác bậc cao có thể tính đến việc hạ bậc của các biểu thức này".
Tuy nhiên, nếu tri thức này không được nêu lên, không được nhấn mạnh và thông báo công khai[21] bởi GV (nghĩa là không được thể chế hóa), thì nó cũng chỉ có thể tồn tại dưới dạng kiến thức của từng cá nhân học sinh. Nói cách khác, một số học sinh có thể nhận ra được kiến thức đó và biết áp dụng về sau. Nhưng cũng có học sinh không rút ra được lợi ích của định hướng phương pháp này, và vì thế sau này có gặp một phương trình bậc cao tương tự họ cũng lúng túng, không biết giải quyết thế nào.
Ngược lại, nếu nó được thể chế hóa và được nhắc lại trong nhiều cơ hội khác, thì dần dần nó là một kiến thức bền vững ở nhiều học sinh.
3. Các hình thức và cấp độ[sửa]
Tuỳ theo vai trò của giáo viên và học sinh trong các bước của dạy học đặt và giải quyết vấn đề cũng như đặc trưng của tri thức đạt được, mà ta phân biệt ba hình thức dạy học chủ yếu sau đây.
a) Tự nghiên cứu giải quyết vấn đề[sửa]
Đây là cấp độ cao nhất của dạy học đặt và giải quyết vấn đề. Nó được đặc trưng bởi các mặt sau đây :
Giáo viên (hoặc cùng học sinh) tạo ra tình huống gợi vấn đề, trình bày vấn đề. Sau khi vấn đề đã được giải quyết, giáo viên có trách nhiệm thực hiện pha thể chế hoá: đánh giá vai trò và ý nghĩa của kết quả đạt được, chuyển kiến thức có tính chất cá nhân thành thành tri thức chung, nhấn mạnh các tri thức phương pháp có thể rút ra từ quá trình nghiên cứu và giải quyết vấn đề.
Học sinh: độc lập tìm cách giải quyết vấn đề, trình bày lời giải, thực hiện pha kiểm tra và đánh giá. Như vậy họ phải hoạt động một cách tích cực, chủ động, tự giác, độc lập và sáng tạo.
Tuỳ theo tình hình mà công việc của học sinh có thể được tổ chức dưới các hình thức khác nhau như :
- Làm việc cá nhân : mỗi học sinh làm việc một cách độc lập.
- Làm việc hợp tác : học sinh làm việc theo nhóm nhỏ, thảo luận, trao đổi trong tất cả các pha của dạy học đặt và giải quyết vấn đề.
- Đan xen giữa hai hình thức làm việc trên.
Tri thức: Không được cho dưới dạng có sẵn, mà xuất hiện trong quá trình hình thành và giải quyết vấn đề, được khám phá bởi chính học sinh.
Ví dụ:
• Giáo viên tạo tình huống gợi vấn đề:
–
Vẽ
lên
bảng
một
tam
giác
ABC
vuông
tại
A,
các
cạnh
tương
ứng
là
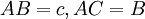 và
và
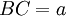 .
.
–
Hỏi:
ta
đã
biết
công
thức
nào
cho
phép
tính
độ
dài
cạnh
BC
theo
hai
cạnh
kia?
Đáp
án
mong
đợi
là
định
lí
Pythagore:
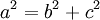
– Tạo tình huống có vấn đề: Như vậy, nếu biết A là góc vuông và độ dài hai cạnh kề nó thì ta có thể tính được độ dài cạnh còn lại. Nếu, bây giờ vẫn cho biết độ lớn góc A và độ dài hai cạnh kề nó, nhưng A là một góc bất kì, liệu có tính được độ dài cạnh thứ ba hay không?
• Giáo viên trình bày vấn đề:
Cho tam giác ABC bất kì. Có thể tìm được hay không công thức tính độ dài cạnh BC nếu biết độ dài hai cạnh còn lại là AC = b, AB = c và độ lớn góc A xen giữa hai cạnh này?
• Học sinh tự giải quyết vấn đề và thực hiện việc đánh giá.
• Giáo viên thực hiện pha thể chế hoá bằng cách trình bày định lí cosin trong tam giác, như là kết quả của việc giải quyết vấn đề trên.
b) Vấn đáp đặt và giải quyết vấn đề[sửa]
Hình thức này có các đặc trưng sau:
Giáo viên xây dựng một hệ thống câu hỏi để gợi ý, dẫn dắt học sinh thực hiện tất cả các pha của dạy học đặt và giải quyết vấn đề, ngoại trừ pha thể chế hoá. Ở mức độ thấp hơn thì chính giáo viên thực hiện việc tạo tình huống có vấn đề và trình bày vấn đề.
Học sinh, nhờ vào hệ thống câu hỏi gợi ý dẫn dắt của giáo viên mà tự giác và tích cực nghiên cứu phát hiện, trình bày và giải quyết vấn đề.
Tri thức không được cho dưới dạng có sẵn và trực tiếp, mà xuất hiện trong quá trình hình thành và giải quyết vấn đề, được khám phá nhờ quá trình tương tác giữa thầy và trò, trong đó trò đóng vai trò chính.
c) Thuyết trình đặt và giải quyết vấn đề[sửa]
Là cấp độ thấp nhất của dạy học đặt và giải quyết vấn đề.
Giáo viên thực hiện tất cả các khâu của hình thức dạy học này: Tạo tình huống gợi vấn đề, trình bày vấn đề, trình bày quá trình suy nghĩ tìm kiếm, dự đoán cách thức giải quyết vấn đề (chứ không đơn thuần trình bày lời giải), … Giáo viên trình bày cả quá trình tìm kiếm của mình, có lúc thành công, có lúc thất bại, có lúc phải điều chỉnh phương hướng nhiều lần mới đi đến kết quả.
Nói cách khác, giáo viên phải đóng vai một học sinh đang tìm cách phát hiện và giải quyết vấn đề : tự đặt ra cho mình các câu hỏi, các nghi vấn, tự mày mò tìm kiếm các phương án giải quyết, rồi tự trả lời, … Điều quan trọng là trong quá trình này, giáo viên cần để lại những “khoảng lặng” để cho học sinh (người học) đủ thời gian cùng tham gia vào quá trình suy nghĩ, tìm kiếm câu trả lời như chính học sinh giả tưởng, chứ không cho câu trả lời ngay sau khi vừa đặt ra một câu hỏi, một nghi vấn nào đó.
Học sinh theo dõi quá trình nghiên cứu đặt và giải quyết vấn đề được trình bày bởi giáo viên. Trong quá trình này, họ cũng trải qua những thời điểm, những cảm xúc và thái độ khác nhau như một học sinh đang thực sự tham gia quá trình nghiên cứu, nhưng không trực tiếp giải quyết vấn đề.
Tri thức, mặc dù không được khám phá bởi chính học sinh, nhưng cũng không được truyền thụ dưới dạng có sẵn và trực tiếp, mà nảy sinh trong quá trình đặt và giải quyết vấn đề của giáo viên.
Chú ý[sửa]
a) Cần phân biệt hình thức vấn đáp đặt và giải quyết vấn đề với phương pháp đàm thoại (hay vấn đáp), hình thức thuyết trình đặt và giải quyết vấn đề với phương pháp thuyết trình. Những điểm khác biệt nhất cần nhấn mạnh là:
– Trong dạy học đặt và giải quyết vấn đề, điều mấu chốt là phải tạo ra các tình huống gợi vấn đề, như V. Okon (bản dịch tiếng việt của Phạm Hoàng Gia, 1976) đã viết:
- “Nét bản chất của dạy học nêu vấn đề không phải là sự đặt ra những câu hỏi mà là tạo ra các tình huống gợi vấn đề” (V. Okon, 1976).
– Kiến thức xuất hiện trong quá trình đặt và nghiên cứu giải quyết vấn đề.
– Học sinh không chỉ lĩnh hội được kiến thức mới như là kết quả của quá trình giải quyết vấn đề, mà còn có thể lĩnh hội được tri thức phương pháp.
– Như vậy, dạy học đặt và giải quyết vấn đề dưới hình thức vấn đáp (hay thuyết trình) cũng là một kiểu dạy học theo phương pháp đàm thoại (hay thuyết trình), nhưng điều ngược lại chưa chắc đúng.
Phát biểu sau đây của I. Ia. Lecne (1981) về hình thức Thuyết trình đặt và giải quyết vấn đề cho phép hiểu rõ hơn sự khác biệt này:
- “Bản chất của hình thức này không những nhằm giới thiệu cho học sinh cách giải quyết đã có đối với các vấn đề nhận thức khoa học hay thực tiễn … mà còn giúp học sinh hiểu logic, những mâu thuẫn và cách giải quyết những mâu thuẫn đó”.
b) Khả năng hoạt động một cách độc lập, tích cực và sáng tạo của học sinh tuỳ thuộc vào hình thức dạy học đặt và giải quyết vấn đề. Chẳng hạn trong hình thức thuyết trình, chính giáo viên thực hiện tất cả các bước của quá trình, học sinh chỉ theo dõi, lắng nghe và lĩnh hội lại tri thức (kể cả tri thức phương pháp) được truyền thụ trực tiếp từ giáo viên. Do vậy, dạy học đặt và giải quyết vấn đề dưới hình thức thuyết trình không thuộc vào nhóm phương pháp dạy học tích cực. Tuy nhiên, nó cũng cho phép phát huy tính tích cực của học sinh, vì trong quá trình đặt và giải quyết vấn đề của giáo viên, học sinh cũng luôn được đặt trong những tình huống khó khăn, nghi vấn, tích cực suy nghĩ, ... Ngoại trừ việc giải quyết các nghi vấn, việc đưa ra phương án giải quyết khó khăn, … là do giáo viên thực hiện.
c) Ta có thể áp dụng dạy học đặt và giải quyết vấn đề không chỉ cho đối tượng học sinh khá giỏi, mà có thể cho cả các đối tượng học sinh khác. Chính với học sinh trung bình hay yếu, việc áp dụng hình thức này một cách thích hợp và hệ thống mới hy vọng giúp họ dần dần thoát khỏi cách học thụ động và lĩnh hội kiến thức một cách tích cực hơn. Hơn nữa, ở cấp độ thấp nhất, với học sinh trung bình hay yếu ta vẫn có thể vận dụng dạy học đặt và giải quyết vấn đề dưới hình thức thuyết trình[22]
d) Trong một giờ lên lớp, nói chung người ta không sử dụng độc nhất một phương pháp dạy học. Do đó, dạy học đặt và giải quyết vấn đề có thể chỉ xuất hiện trong một số công đoạn của giờ lên lớp. Hơn nữa, cũng cần tránh quan điểm cực đoan phải áp dụng hình thức dạy học này cho mọi nội dung cần giảng dạy.
Mặt khác, ngay cả khi áp dụng dạy học đặt và giải quyết vấn đề thì đôi khi ta không thể tuân thủ cứng nhắc một hình thức nào trong ba hình thức trên. Tuỳ diễn tiến của tình huống mà các hình thức này có thể được áp dụng đan xen nhau, hỗ trợ cho nhau.
4. Một số cách tạo ra tình huống có vấn đề[sửa]
Để thực hiện dạy học phát hiện và giải quyết vấn đề cho giờ học hay cho một đơn vị kiến thức nào đó của giờ học, điểm xuất phát là tạo ra tình huống gợi vấn đề, tốt nhất là tình huống gây được cảm xúc và làm cho học sinh ngạc nhiên.
Sau đây là một số cách tạo ra các tình huống "có vấn đề", chứ chưa phải là tình huống "gợi vấn đề". Để chúng trở thành các tình huống "gợi vấn đề" cần phải đảm bảo rằng tình huống gợi ra ở học sinh nhu cầu nhận thức và niềm tin ở khả năng.
- Xem chi tiết: Tạo tình huống có vấn đề trong dạy học môn Toán
5. Dạy học giải quyết vấn đề các loại kiến thức đặc thù[sửa]
Mục này được viết phỏng theo: Dạy học phát hiện và giải quyết vấn đề trong môn Vật lí#2. Dạy học giải quyết vấn đề các loại kiến thức đặc thù. Tại sao lại theo tài liệu này? Vì cách chia các bước thể hiện rõ ràng và hợp lí hơn.
| Các pha/ bước của dạy học phát hiện và giải quyết vấn đề | Khái niệm | Định lí | Tri thức phương pháp có tính thuật toán | Tri thức phương pháp tìm đoán |
|---|---|---|---|---|
| 1. Làm nảy sinh VĐ cần giải quyết từ tình huống (điều kiện) xuất phát: từ kiến thức cũ, kinh nghiệm, TN, bài tập, truyện kể lịch sử… |
Xây dựng biểu tượng về hiện tượng: Thông qua tái hiện kinh nghiệm, thí nghiệm, clips, ảnh… |
Tùy theo hình thành đặc điểm định lượng hay định tính trước mà có cách đặt vấn đề khác nha: Cơ bản đều phải làm bật ra nhu cầu cần xây dựng đại lượng mới để diễn tả tính chất vật lí mà các đại lượng đã có không mô tả được đầy đủ |
Dùng thí nghiệm, kinh nghiệm sơ bộ chỉ ra mối quan hệ giữa các đại lượng. |
Đưa ra một nhu cầu, nhiệm vụ cần thực hiện mà những thiết bị kĩ thuật (TBKT) đã biết chưa thể thực hiện được hoặc thực hiện chưa tốt. |
|
2. Phát biểu VĐ cần giải quyết (câu hỏi cần trả lời) |
Khi nào thì xảy ra hiện tượng này? Khi ... thì xảy ra hiện tượng gì? Tại sao lại xảy ra hiện tượng ...? |
Đặc tính … phụ thuộc vào các đại lượng nào và phụ thuộc như thế nào vào các đại lượng đó? Biểu thức… đặc trưng cho tính chất vật lí nào? |
Mối quan hệ giữa các đại lượng A và B là gì? A và B có mốt quan hệ với nhau như thế nào? A phụ thuộc vào B,C… như thế nào? |
Máy (TBKT) phải có nguyên tắc cấu tạo và hoạt động như thế nào để thực hiện được chức năng ? |
|
3. Giải quyết VĐ - Suy đoán giải pháp GQVĐ: nhờ khảo sát lí thuyết và/hoặc khảo sát thực nghiệm - Thực hiện giải pháp đã suy đoán |
Kiểm tra kết luận: Đưa ra giả thuyết Dùng thí nghiệm kiểm tra (VD: hiện tượng tán sắc, khúc xạ..) Hoặc suy luận lí thuyết để rút ra hệ quả rồi dùng TN kiểm tra (VD: hiện tượng sóng dừng, hiện tượng giao thoa) |
Xây dựng thí nghiệm để trả lời câu hỏi vấn đề |
- Xây dựng giả thuyết và thiết kế phương án thí nghiệm kiểm tra giả thuyết. - Sử dụng các kiến thức lí thuyết đã có để suy luận lô gic rút ra câu trả lời rồi dùng thí nghiệm kiểm nghiệm lại kết quả |
Mở máy ra và xác định các bộ phận chính, các quy luật cơ bản chi phối. Xây dựng mô hình hình vẽ (MHHV) và tiến hành thí nghiệm kiểm tra xem MHHV có thực hiện được đúng các chức năng của TBKT không Thiết kế một TBKT để đáp ứng được yêu cầu đặt ra. Lựa chọn thiết kế tối ưu và xây dựng mô hình vật chất chức năng (VC –CN) theo thiết kế và vận hành thử. |
|
4. Rút ra kết luận (kiến thức mới) |
Định nghĩa khái niệm về đối tượng, về phép toán |
Phát biểu định lí Phát biểu công thức |
Phát biểu định luật và phạm vi áp dụng định luật |
Rút ra nguyên tắc cấu tạo và hoạt động của TBKT |
|
5. Vận dụng kiến thức mới để giải quyết những nhiệm vụ đặt ra tiếp theo |
Nhận biết các biểu hiện của hiện tượng đã học trong tự nhiên. |
Vận dụng đại lượng để mô tả các đặc tính vật lí ở các hiện tượng khác nhau. |
Vận dụng định luật trong các hiện tượng vật lí khác. |
So sánh TBKT đã xây dựng với các TBKT trong đời sống để bổ sung các yếu tố khác. |
6. Ví dụ minh họa[sửa]
Ví dụ 1: Giải bpt dạng A^2.B ≤ 0[sửa]
Khi dạy phần bất phương trình ở lớp 10 có thể cho HS giải bài tập sau:
Khi
giải
bất
phương
trình
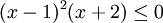 (1),
bạn
Hòa
đã
giải
như
sau:
(1),
bạn
Hòa
đã
giải
như
sau:
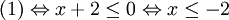 (2)
(2)
Vậy
tập
nghiệm
của
bất
phương
trình
đã
cho
là
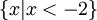
Xét xem lời giải trên đã đúng chưa? Nếu chưa đúng, hãy sửa lại.
Khi giải bài toán này, HS được đặt vào một tình huống gợi vấn đề với nhiệm vụ là phát hiện nguyên nhân và sửa chữa sai lầm. Đó là một tình huống gợi vấn đề vì đối chiếu với ba điểu kiện của tình huống gợi vấn đề, ta thấy:
- HS chưa có sẵn câu trả lời và cũng không biết một thuật giải nào để có câu trả lời
- HS có nhu cầu giải quyết vấn đề, họ không thể chấp nhận để nguyên nhân sai lầm mà không sửa chữa
- Vấn đề này liên quan đến những kiến thức sẵn có của họ, không có gì vượt quá yêu cầu, họ thấy nếu tích cực suy nghĩ vận dụng kiến thức đã học thì có thể tìm ra nguyên nhân sai lầm và sửa chữa sai lầm.
| Bước | Hoạt động |
|---|---|
| 1. Phát hiện hoặc thâm nhập vấn đề |
Sau
khi
ra
đề,
GV
dành
thời
gian
để
HS
suy
nghĩ
xem
xét
lời
giải
đã
đúng
chưa.
Nếu
sai
thì
sai
ở
điểm
nào?
Nếu
HS
chưa
phát
hiện
được
sai
lầm
thì
GV
có
thể
gợi
ý
để
HS
thấy
được
bất
phương
trình
còn
có
nghiệm
khác,
chẳng
hạn
|
| 2. Tìm giải pháp |
Sau
khi
cho
HS
tìm
kiếm,
tạo
điều
kiện
để
HS
chỉ
ra
được
các
sai
lầm
trong
lời
giải:
1)
Sai
lầm
là
do
việc
viết:
Đúng
ra:
(Sai lầm này HS rất khó nhận ra) 2) Sai lầm thứ hai là việc viết tập nghiệm chưa đúng. |
| 3. Trình bày giải pháp |
Từ
việc
chỉ
ra
những
sai
lầm
đó,
HS
có
thể
đưa
ra
được
lời
giải
đúng:
Vậy
bất
phương
trình
đã
cho
có
nghiệm
là
|
| 4. Rút ra kết luận |
Cách
giải
bất
phương
trình
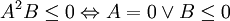
|
| 5. Nghiên cứu sâu giải pháp |
Từ
việc
giải
bất
phương
trình
trên,
có
thể
suy
ra
cách
giải
tương
tự
cho
các
bất
phương
trình
có
dạng
|
Ví dụ 2. Đặt ẩn phụ biện luận phương trình có tham số[sửa]
Khi dạy phần Bất phương trình theo chương trình Đại số 10 nâng cao có thể yêu cầu HS giải bài tập sau:
Tìm
các
giá
trị
của
tham
số
m
để
phương
trình
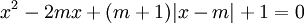 (1)
(1)
a) Có hai nghiệm phân biệt
b) Có bốn nghiệm phân biệt
Đây là bài toán mà thoạt nhìn thì HS không thấy thuộc loại toán cơ bản nào đã xét. Khi giải bài toán này HS cũng được đặt vào một tình huống gợi vấn đề.
| Bước | Hoạt động |
|---|---|
| 1. Phát hiện hoặc thâm nhập vấn đề | Các em đã biết cách tìm điều kiện để một phương trình bậc hai có số nghiệm cho trước: có hai nghiệm, một nghiệm hoặc vô nghiệm. Các em cũng đã biết giải bài toán về số nghiệm của một phương trình trùng phương. Liệu có thể giải bài toán về số nghiệm của phương trình có chứa ẩn trong dấu giá trị tuyệt đối như ở phương trình (1) hay không? |
| 2. Tìm giải pháp |
GV
tạo
điều
kiện
để
HS
nêu
cách
giải
quyết
của
các
em.
Nhiều
HS
thường
nêu
cách
giải:
phá
dấu
giá
trị
tuyệt
đối,
sau
đó
với
mỗi
trường
hợp
nêu
điều
kiện
để
phương
trình
có
hai
nghiệm
phân
biệt,...
Cho HS thảo luận xem liệu những cách HS đưa ra có phù hợp không? Khi giải có khó khăn gì không?
Sau
đó
GV
có
thể
gợi
ý
để
HS
thấy
mối
liên
hệ
giữa
(Có thể liên hệ với phần b Bài 27, trang 85, SGK Đại số 10 nâng cao:
"Bằng
cách
đặt
ẩn
phụ,
giải
phương
trình
Từ đó, HS thấy được phép đặt ẩn phụ là:
Đặt
Mỗi nghiệm dương của phương trình (2) ứng với hai nghiệm của phương trình (1), mỗi nghiệm bằng 0 của phương trình (2) ứng với một nghiệm của phương trình (1). Đến đây, HS thấy được cách giải quyết bài toán này gần giống bài toán về số nghiệm của phương trình trùng phương có ở SGK. |
| 3. Trình bày giải pháp | HS trình bày quá trình giải quyết bài toán: từ việc đặt ẩn phụ, lập luận về mối liên hệ giữa nghiệm của phương trình trung gian và số nghiệm của phương trình ban đầu đến việc giải quyết trọn vẹn bài toán. |
| 4. Nghiên cứu sâu giải pháp |
Sau
khi
đặt
ẩn
phụ
thì
cách
lập
luận
tương
tự
như
cách
biện
luận
số
nghiệm
của
phương
trình
trùng
phương,
do
đó
có
thể
yêu
cầu
HS
giải
những
yêu
cầu
tương
tự:
Tìm
m
để
phương
trình
(1)
có
ba
nghiệm
phân
biệt;
có
đúng
1
nghiệm;
vô
nghiệm.
Từ
bài
toán
trên,
bằng
cách
tương
tự
có
thể
giải
các
bài
toán
về
số
nghiệm
của
phương
trình:
(Với
bài
tập
này
HS
có
thể
đặt
ẩn
phụ
|
Ví dụ 3[sửa]
- Xem chi tiết: Lựa chọn, sử dụng một số phương pháp dạy học toán ở tiểu học#c) Trường hợp 3: Hình thành tri thức mới, có mâu thuẫn
Chú thích[sửa]
- ↑ Học sinh đã học định lí về tổng các góc trong của một tam giác
- ↑ Ở THCS chỉ xét các tứ giác lồi
- ↑ Hướng đích và gợi động cơ#Quy lạ về quen
- ↑ Theo Wiktionary: Tình huống là toàn thể những sự việc xảy ra tại một nơi, trong một thời gian, buộc người ta phải suy nghĩ, hành động, đối phó, chịu đựng...
- ↑ Hiểu như vậy thì vấn đề không đồng nghĩa với bài toán. Vì có những bài toán chỉ yêu cầu học sinh đơn thuần trực tiếp áp dụng một thuật giải, chẳng hạn giải phương trình bậc hai dựa vào công thức đã học, thì những bài toán đó không phải là vấn đề
- ↑ Phúc: Do đó, PPDH này rất phù hợp để dạy các tri thức phương pháp
- ↑ Thường là GV làm nảy sinh VĐ cần giải quyết từ tình huống có vấn đề và HS phát hiện vấn đề
- ↑ Phát biểu VĐ cần giải quyết (câu hỏi cần trả lời)
- ↑ Suy đoán giải pháp GQVĐ
- ↑ Thu thập thông tin có liên quan đến vấn đề/tình huống đặt ra
-
↑
-
Liệt
kê
các
cách
giải
quyết
có
thể
có;
- Phân tích, đánh giá kết quả mỗi cách giải quyết (tích cực, hạn chế, cảm xúc, giá trị) ;
- So sánh kết quả các cách giải quyết;
- Lựa chọn cách giải quyết thích hợp; - ↑ Thực hiện theo giải pháp đã lựa chọn. Trình bày lời giải
- ↑ Kiến thức mới
- ↑ Cách giải hay, cách giải ngắn, cách giải hiệu quả, cách giải tổng quát,...
- ↑ Khái niệm, định lý, công thức
- ↑ Cách tư duy, phân tích, phương pháp, kĩ thuật nhận thức, tìm đoán suy luận
- ↑ Tức là giáo viên truyền thụ tường minh hoặc thông báo tri thức này. Xem thêm: Tri thức và tri thức phương pháp
- ↑ Bước này không nhất thiết phải có và nếu có thì các bài tập ở mức giải quyết vấn đề hoặc gắn với bối cảnh, tình huống thực tiễn. Xem: Định hướng xây dựng câu hỏi, bài tập đánh giá năng lực học sinh
- ↑ Bao gồm cả cách thức tìm kiếm lời giải
- ↑ Rút kinh nghiệm cho việc giải quyết những vấn đề, tình huống khác
- ↑ Trong thực tế dạy học, các giáo viên thường gọi là Chốt
- ↑ Tham khảo thêm Nguyễn Bá Kim (1991).
Tài liệu tham khảo[sửa]
- Phương pháp dạy học môn Toán, Nguyễn Bá Kim, 2011
- Phương pháp dạy học các tình huống điển hình trong môn Toán, Lê Văn Tiến, 2005



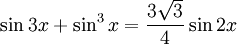
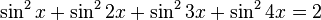
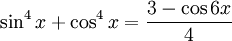
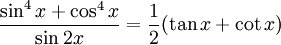
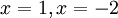 .
.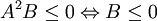
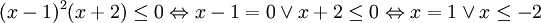
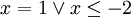
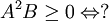
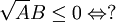
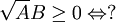
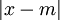 và
và
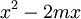 .
.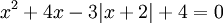 ")
")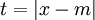 ,
với
,
với
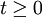 .
Phương
trình
đã
cho
được
chuyển
thành:
.
Phương
trình
đã
cho
được
chuyển
thành:
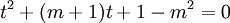 (2)
(2)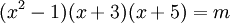
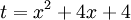 rồi
giải
tương
tự
như
phương
trình
trùng
phương).
rồi
giải
tương
tự
như
phương
trình
trùng
phương).

