Tri thức và tri thức phương pháp

Sau mỗi quá trình học tập, người học không chỉ đơn thuần thu được những tri thức khoa học (khái niệm mới, định lí mới,... ) mà còn phải nắm được những tri thức phương pháp (dự đoán, giải quyết, nghiên cứu...). Đó chính là những tri thức phương pháp vừa là kết quả vừa là phương tiện của hoạt động tạo cho học sinh một tiềm lực quan trọng để hoạt động tiếp theo.

Ảnh minh họa

Các dạng tri thức thường gặp

Các tri thức truyền thụ cho học sinh trong quá trình dạy học thường có các dạng:

1. Tri thức sự vật: Những hiểu biết về hiện thực khách quan mà con người đã tích lũy được. Trong môn toán đó là: khái niệm, định lí, có khi là một yếu tố lịch sử.
2. Tri thức phương pháp: Gồm có hai loại, phương pháp có tính chất thuật toán và phương pháp có tính chất tìm đoán.
3. Tri thức chuẩn: Những kiến thức có liên quan đến chuẩn mực đạo đức (ít gặp ở môn Toán).
4. Tri thức giá trị: Có nội dung là những mệnh đề đánh giá. Ví dụ như: "Khái quát hóa là một thao tác trí tuệ cần thiết cho mọi khoa học" hay "phép tương tự có lẽ là có mặt trong mọi phát minh và trong một số phát minh nó chiếm vai trò quan trọng hơn cả". (Theo G.Polya)

Trong những dạng tri thức kể trên thì tri thức phương pháp đóng một vai trò quan trọng trong việc tổ chức hoạt động vì đó là cơ sở định hướng cho hoạt động.

Những tri thức phương pháp thường gặp trong dạy học toán

Những tri thức phương pháp trong dạy học toán có thể gặp khi tiến hành:

1. Những hoạt động toán học cụ thể như cộng hai phân số không cùng mẫu số, giải phương trình asin² x + bsin x + c = 0...
2. Những hoạt động trí tuệ phổ biến như phân chia các trường hợp, tư duy hàm,...
3. Những hoạt động trí tuệ chung như phân tích, tổng hợp, so sánh, khái quát hóa, tương tự,...
4. Những hoạt động ngôn ngữ logic như lập mệnh đề đảo, liên kết các mệnh đề nhờ các phép nối logic, điều kiện cần và đủ,...

Biện pháp thực hiện

Để tổ chức hoạt động có hiệu quả, người giáo viên cần nắm được tất cả những kiến thức phương pháp thích hợp có thể có chứa đựng trong nội dung bài dạy để chọn lựa cách thức, mức độ truyền thụ phù hợp. Bởi vì, những tri thức quá chung như lược đồ dựng hình 4 bước sẽ ít tác dụng hướng dẫn nhưng nếu quá chi tiết thì khó áp dụng cho các tình huống khác.

Đứng trước một nội dung dạy học, người giáo viên phải:

1. Xác định tập hợp tối thiểu những tri thức phương pháp cần truyền thụ.
2. Xác định yêu cầu về mức độ hoàn chỉnh của những tri thức phương pháp có tính chất tìm đoán. Những tri thức phương pháp quá chung sẽ ít tác dụng chỉ dẫn, điều khiển hoạt động. Mặt khác, những tri thức phương pháp rậm rạp lại có thể làm cho học sinh lâm vào tình trạng rối ren.
3. Xác định yêu cầu về mức độ tường minh của những tri thức phương pháp cần truyền thụ: truyền thụ tường minh hay là thông báo nhân quá trình tiến hành hoạt động, hay chỉ thực hiện ăn khớp với tri thức nào đó, hay là một hình thức trung gian giữa hình thức kể trên.
4. Xác định yêu cầu về mức độ chặt chẽ của quá trình hình thành tri thức phương pháp: dựa vào trực giác hay lập luận logic.

Những vấn đề trên hiện nay còn chưa được nghiên cứu đầy đủ. Tuy nhiên người có trách nhiệm giải quyết trước hết không phải là giáo viên mà là những người làm chương trình, viết sách giáo khoa.

Ví dụ:

TTPP cần truyền thụ	Cách truyền thụ			Hoạt động của GV
	Mức độ tường minh	Mức độ hoàn chỉnh	Mức độ chặt chẽ
1. Tri thức phương pháp có tính thuật toán	Dạy học một cách tường minh	Đầy đủ 3 bước	Lập luận logic
2. Tri thức phương pháp tìm đoán	Thông báo tường minh	Định hướng chung	Trực giác/trực quan	Thông báo trong quá trình dạy học. Thông báo này có thể được lặp lại trong nhiều cơ hội khác nhau, ở những thời điểm khác nhau.
3. Cả hai	Truyền thụ ngầm ẩn	Chiến lược	Lập luận logic	Tổ chức cho HS thực hiện nhiều hoạt động tương thích với một chiến lược, một định hướng giải quyết chung

Các mức độ truyền thụ tri thức phương pháp:

Truyền thụ tường minh những tri thức phương pháp đã quy định trong chương trình

Xem chi tiết: Tri thức phương pháp/Truyền thụ tường minh

Đối với những tri thức phương pháp quy định trong chương trình cần xuất phát từ chương trình và sách giáo khoa để lĩnh hội được mức độ hoàn chỉnh, mức độ tường minh và mức độ chặt chẽ của quá trình hình thành những tri thức phương pháp đó.

Một điều quan trọng trong việc truyền thụ và củng cố những tri thức phương pháp là nên phối hợp nhiều cách thể hiện những phương pháp đó.

Ví dụ: Phương pháp giải phương trình bậc hai tổng quát, các bước tiến hành để xây dựng đạo hàm,...

Thông báo tri thức phương pháp trong quá trình tiến hành hoạt động

Xem chi tiết: Tri thức phương pháp/Thông báo

Đối với những tri thức phương pháp chưa được quy định trong chương trình, ta vẫn có thể suy nghĩ khả năng thông báo chúng trong quá trình học sinh tiến hành hoạt động nếu những tiêu chuẩn sau đây được thỏa mãn:

1. Những tri thức phương pháp này giúp học sinh dễ dàng thực hiện một số hoạt động quan trọng nào đó được quy định trong chương trình.
2. Việc thông báo những tri thức này là dễ hiểu và tốn ít thời gian.

Ví dụ 1: Chứng minh định lí về tổng các góc trong của một tam giác.

Nhân việc kẻ thêm đường phụ trong khi chứng minh định lí này, có thể thông báo cho học sinh những tri thức phương pháp sau đây:

• Để tìm cách chứng minh một định lí, có khi phải vẽ thêm đường phụ.
• Việc vẽ thêm một đường phụ là xuất phát từ việc phân tích kĩ giả thiết và kết luận.

Ví dụ 2: Khi giải và biện luận phương trình 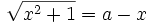${\sqrt {x^{2}+1}}=a-x$ sách giáo khoa dùng phép biến đổi hệ quả để đi đến 2ax = a² - 1 rồi thay vào phương trình đầu để lấy nghiệm nếu có phần phức tạp trong tính toán. Ta có thể hướng dẫn học sinh đặt thêm điều kiện phụ x ≤ a và coi đó là phép biến đổi tương đương rồi xét:

• a = 0 phương trình vô nghiệm.
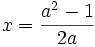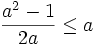• a ≠ 0 thì $x={\frac {a^{2}-1}{2a}}$ với ${\frac {a^{2}-1}{2a}}\leq a$ . Điều này chỉ thỏa mãn với x > 0.

Qua đây, ta cung cấp cho học sinh một phương pháp biến đổi tương đương các phương trình chứa căn thức thường gặp nhưng sách giáo khoa không trình bày.

Chú ý rằng: Có thể những tri thức phương pháp này chưa làm ta thỏa mãn vì chúng cung cấp ít thông tin cho việc giải quyết bài toán. Nhưng vấn đề là ở chỗ: liệu nội dung tương ứng, liệu mục đích dạy học nội dung đó, liệu quỹ thời gian và những yếu tố khác có cho phép ta thông báo những tri thức phương pháp đó chi tiết hơn và có hiệu lực chỉ dẫn hoạt động tốt hơn hay không. Dù sao thì những tri thức phương pháp đó cũng giúp ích ít nhiều cho việc giải quyết bài toán đã đặt ra.

Tập luyện những hoạt động ăn khớp với những tri thức phương pháp

Xem chi tiết: Tri thức phương pháp/Tập luyện

Đối với những tri thức phương pháp không quy định chương trình mà chỉ thỏa mãn tiêu chuẩn thứ nhất chứ không thỏa mãn tiêu chuẩn thứ hai đã nêu ở mục trên thì ta có thể đề cập ở mức độ thấp nhất: Chỉ tập luyện những hoạt động ăn khớp với những tri thức phương pháp đó.

Những tri thức như thế cần được giáo viên vận dụng một cách có ý thức trong việc ra bài tập, trong việc hướng dẫn và bình luận hoạt động của học sinh. Nhờ đó học sinh được làm quen với những phương pháp tương ứng và nhận ra sự cần thiết của những phương pháp này.

Ví dụ 1: Rèn luyện khả năng chứng minh hình học.

Ví dụ này được trình bày dựa theo Walsch, 1975.

Một con đường có hiệu quả để phát triển ở học sinh năng lực chứng minh toán học là tạo điều kiện cho họ tập luyện dần dần những hoạt động ăn khớp với một chiến lược giải toán chứng minh hình học. Chiến lược này kết tinh lại ở học sinh như một bộ phận kinh nghiệm mà họ thu lượm được trong quá trình giải những bài toán này (mưa dầm thấm đất, cát bồi phù sa). Đương nhiên, sự kết tinh này không nên để diễn ra một cách tự phát mà trái lại cần có những biện pháp được thực hiện một cách có mục đích, có ý thức của giáo viên. Giáo viên luôn luôn lặp đi lặp lại một cách có dụng ý những chỉ dẫn hoặc câu hỏi như:

• Hãy vẽ một hình theo những dữ kiện của bài toán. Những khả năng có thể xảy ra?
• Giả thiết nói gì? Giả thiết còn có thể biến đổi như thế nào?
• Từ giả thiết suy ra được điều gì? Những định lí nào có giả thiết giống hoặc gần giống với giả thiết của bài toán?
• Kết luận nói gì? Điều đó còn có thể được phát biểu như thế nào?
• Những định lí nào có kết luận giống hoặc gần giống với kết luận của bài toán?
• Đã biết bài toán nào tương tực hay chưa?
• Cần có kẻ thêm đường phụ hay không?
• ...

Những chỉ dẫn kiểu như các câu hỏi này gắn liền với những bài toán cụ thể nhưng được phát biểu một cách tổng quát để học sinh có thể vận dụng vào những tình huống tương khác nữa. Với thời gian, họ sẽ ý thức được những câu hỏi hoặc chỉ dẫn này được giáo viên sử dụng lặp đi lặp lại nhiều lần, sẽ dần dần lĩnh hội và vận dụng chúng như một chiến lược giải toán chứng minh hình học.

Minh họa: Tổ chức cho học sinh hoạt động để giải bài toán "Cho đường tròn C(O;R) và một điểm M sao cho OM = 3R. Một đường kính AB di động quanh O. Chứng minh rằng đường tròn ngoại tiếp tam giác MAB luôn đi qua một điểm cố định."

Những hoạt đông có thể tổ chức là:

• Hãy vẽ hình và ghi các kí hiệu.
• Những yếu tố nào không đổi, cố định?
• Mối liên hệ giữa các yếu tố này với yêu cầu của đề bài?
• Dự đoán điểm cố định và chứng minh.

Ví dụ 2: Rèn luyện khả năng tìm đoán.

Sau khi học sinh đã học định lí Côsi với hai số và bốn số không âm. Ta có thể tổ chức cho học sinh tìm đoán cách chứng minh bất đẳng thức cho trường hợp ba số không âm như sau:

• Sau khi chứng minh trường hợp 2, 4 số ta có gì trong tay?

${\frac {a_{1}+a_{2}}{2}}\geq {\sqrt {a_{1}.a_{2}}}$

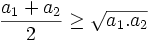(1)

và

${\frac {a_{1}+a_{2}+a_{3}+a_{4}}{4}}\geq {\sqrt[ {4}]{a_{1}.a_{2}.a_{3}.a_{4}}}$

(2)

• Ta phải chứng minh điều gì?

${\frac {a_{1}+a_{2}+a_{3}}{3}}\geq {\sqrt[ {3}]{a_{1}.a_{2}.a_{3}}}$ (3)

• Hãy xét chứng minh bất đẳng thức (2) và xem có thể áp dụng cách ấy để chứng minh (3) không? (Trường hợp này không sử dụng (1) được vì số số hạng bị "lẻ"). Vậy ta chỉ còn cách sử dụng (2). Muốn vậy phải có 4 số không âm mà vế trái của (3) chỉ có 3 số hạng không âm. Nên ta phải thêm vào đó một số hạng thứ tư, gọi là x sao cho x phải không âm và không được làm thay đổi (3)!

• Tìm x?

Ta giải phương trình

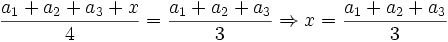${\frac {a_{1}+a_{2}+a_{3}+x}{4}}={\frac {a_{1}+a_{2}+a_{3}}{3}}\Rightarrow x={\frac {a_{1}+a_{2}+a_{3}}{3}}$ và x ≥ 0.

• Hãy áp dụng (2) với 4 số a₁, a₂, a₃, x không âm:

${\frac {a_{1}+a_{2}+a_{3}}{3}}={\frac {a_{1}+a_{2}+a_{3}+x}{4}}\geq {\sqrt[ {4}]{a_{1}.a_{2}.a_{3}.x}}$ (4)

Nếu a₁ = a₂ = a₃ = x bất đẳng thức rõ ràng thỏa mãn.

Chỉ còn xét a₁, a₂, a₃, x > 0.

• Ta gặp một trở ngại nhỏ: ở vế phải của (4) ta cần căn bậc 3 nhưng lại có căn bậc 4! Hãy lưu ý biểu thức của x và tìm cách biến đổi:

(4) $\Leftrightarrow \left({\frac {a_{1}+a_{2}+a_{3}}{3}}\right)^{4}\geq a_{1}.a_{2}.a_{3}.x=a_{1}.a_{2}.a_{3}.{\frac {a_{1}+a_{2}+a_{3}}{3}}$

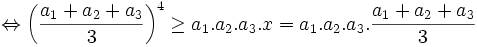
$\Leftrightarrow \left({\frac {a_{1}+a_{2}+a_{3}}{3}}\right)^{3}\geq a_{1}.a_{2}.a_{3}\Leftrightarrow {\frac {a_{1}+a_{2}+a_{3}}{3}}\geq {\sqrt[ {3}]{a_{1}.a_{2}.a_{3}}}$

• Tổng kết lại những kết quả ta đã đạt được và cho biết bằng phương pháp tương tự ta sẽ chứng minh được những trường hợp nào nữa? Dự đoán trường hợp tổng quát với n số không âm?

${\frac {a_{1}+a_{2}+a_{3}+...+a_{n}}{n}}\geq {\sqrt[ {n}]{a_{1}.a_{2}.a_{3}...a_{n}}}$

Tài liệu tham khảo

• Giáo trình PPDH môn Toán, phần đại cương, Nguyễn Bá Kim, Vũ Dương Thụy, Nhà xuất bản giáo dục, 2000, 87. (khai thác chưa hết)
• Giáo trình PPDH môn Toán, phần đại cương, Trần Khánh Hưng, Nhà xuất bản giáo dục, 1998, 61.

Bài liên quan

• Phân bậc hoạt động
• Hướng đích và gợi động cơ
• Phát hiện, chọn lựa các hoạt động tương thích với nội dung
• Những thành tố cơ sở của phương pháp dạy học toán

Liên kết đến đây

• Những thành tố cơ sở của phương pháp dạy học toán
• Thành viên:Nguyenthephuc/Note: Cách giảng dạy để học sinh tự học
• Dạy học phát hiện và giải quyết vấn đề trong môn Toán học
• Bốn đặc trưng cơ bản của phương pháp dạy học tích cực
• Dạy học tri thức phương pháp