Phát hiện, chọn lựa các hoạt động tương thích với nội dung

Mỗi nội dung dạy học đều liên hệ mật thiết với những hoạt động nhất định. Do đó giáo viên phải biết phát hiện những hoạt động thành phần tiềm ẩn trong nội dung, chọn lựa những hoạt động tương thích với nội dung, mục đích dạy học và cho học sinh thực hiện và tập luyện các hoạt động đó.

Hoạt động tương thích là gì?

Hoạt động được gọi là tương thích với nội dung nếu nó được tiến hành trong quá trình hình thành hoặc vận dụng nội dung đó.

Nói cách khác, một hoạt động là tương thích với nội dung nếu việc nắm được nội dung này là điều kiện hay kết quả (đọng lại trong chủ thể) của hoạt động đó.

Các dạng hoạt động sau cần chú ý:

1. Những hoạt động nhận dạng và thể hiện: một khái niệm, một phương pháp, một quy tắc, một định lí
2. Những hoạt động toán học phức hợp: chứng minh, định nghĩa, giải toán dựng hình, giải toán quỹ tích, giải toán bằng cách lập phương trình,...
3. Những hoạt động trí tuệ phổ biến trong môn toán : lật ngược vấn đề, xét tính giải được (có nghiệm, nghiệm duy nhất,...), phân chia trường hợp,...
4. Những hoạt động trí tuệ chung: phân tích, tổng hợp, so sánh, xét tương tự, trừu tượng hóa, khái quát hóa,...
5. Những hoạt động ngôn ngữ: khi yêu cầu học sinh phát biểu, giải thích một định nghĩa, trình bày lời giải một bài toán,...

Chọn lựa các hoạt động tương thích

1) Tập trung vào mục đích/mục tiêu đã đề ra.

Ví dụ: Khi dạy về tìm công thức giải phương trình bậc hai tổng quát ax² + bx + c = 0 ta tập trung vào các hoạt động để đưa phương trình trên về dạng (x + A)² = B (trong đó A và B không chứa x) vì đây là mục đích chính của giờ dạy.

2) Phân tích hoạt động thành những hoạt động thành phần.

Để chọn được các hoạt động tương thích ta phải phân tích hoạt động thành những hoạt động thành phần.

Ví dụ: Khi cho học sinh chứng minh một định lí, giải một bài tập (hoạt động phức hợp) mà gặp khó khăn ta phải tách ra thành những hoạt động nhỏ hơn:

• Từ giả thiết ta có thể suy ra điều gì?
• Muốn có kết luận ta cần có những điều kiện gì?
• Hãy xét một trường hợp đặc biệt, một trường hợp tương tự.

Những hoạt động thành phần này không những giúp học sinh tìm ra đường lối giải được bài toán (hoạt động mang tính chất điều kiện) mà còn hiểu sâu hơn (mang tính chất kết quả).

3) Tập trung vào những hoạt động toán học: nhận dạng và thể hiện, những hoạt động toán học phức hợp, những hoạt động trí tuệ phổ biến trong môn toán.

Trong những hoạt động để đạt được mục đích ta cần phải phân biệt hai chức năng của nó: chức năng phương tiện và chức năng mục đích. Đương nhiên cả hai đều cần thiết và quan trọng, nhưng ta cần chú ý đến chức năng mục đích của giờ dạy toán.

Ví dụ: Để dạy một định lí, giải một bài toán ta xét các trường hợp cụ thể, hình vẽ, mô hình,... rồi quan sát, nhận xét,... (chức năng phương tiện) nhưng ta cần đặc biệt lưu ý đến chức năng toán học như chứng minh, phương pháp giải toán, nhận dạng, thể hiện,...

Ví dụ 1: Để dạy cho học sinh lớp 9 nắm vững nội dung định lí "Tứ giác nội tiếp trong đường tròn" ta cần tổ chức các hoạt động sau:

1) Hoạt động trí tuệ: Bất kì tam giác nào cũng nội tiếp được trong một đường tròn, điều đó còn đúng không nếu đó là tứ giác? Ví dụ hình bình hành, hình chữ nhật? Cho bốn điểm A, B, C, D nằm trên một đường tròn tạo nên một tứ giác lồi. Cho biết góc A = 60°, hãy dùng kiến thức về góc nội tiếp tìm độ lớn của góc C. Từ đó nêu lên một giả thuyết và chứng minh.

2) Hoạt động nhận dạng, thể hiện: Hãy xét các tứ giác hình bình hành, hình chữ nhật, hình vuông, hình thang cân, thang thường, xem hình nào nội tiếp được, không được?

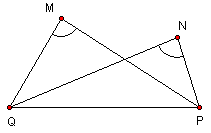
3) Hoạt động phức hợp: Để chứng minh một tứ giác ABCD là nội tiếp được trong một đường tròn có cần phải có điều kiện A + C = 180° và B + D = 180° không? Tại sao? Với các điều kiện trong hình bên, ta có thể kết luận tứ giác MNPQ nội tiếp trong một đường tròn được không? Cho biết ABCD nội tiếp được trong một đường tròn, hãy vẽ đường tròn đó!

4) Hoạt động ngôn ngữ: Hãy phân biệt: Đường tròn (O) ngoại tiếp tứ giác ABCD và tứ giác ABCD nội tiếp đường tròn (O)!

Ví dụ 2: Dạy học khái niệm "Hàm số liên tục tại một điểm".

1) Hoạt động trí tuệ: Cho hàm số y = f(x) = 2x + 3, hãy tính f(1) và 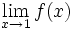$\lim _{{x\rightarrow 1}}f(x)$ . So sánh hai giá trị vừa tìm được. Ta nói hàm số đã cho liên tục tại điểm x = 1. Hãy phát biểu trong trường hợp tổng quát!

2) Hoạt động nhận dạng, thể hiện: Xét xem một hàm số cụ thể:

Ví dụ hàm số:

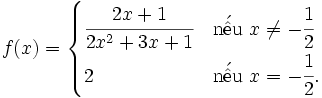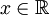$f(x)={\begin{cases}{\cfrac {2x+1}{2x^{2}+3x+1}}&{\mbox{n}}{\acute {{\hat {{\mbox{e}}}}}}{\mbox{u}}\ x\neq -{\cfrac 12}\\2&{\mbox{n}}{\acute {{\hat {{\mbox{e}}}}}}{\mbox{u}}\ x=-{\cfrac 12}.\end{cases}}$ có liên tục với mọi $x\in {\mathbb {R}}$ không, nếu không hãy chỉ ra các điểm gián đoạn.

3) Hoạt động phức hợp:

Cho hàm số $f(x)={\begin{cases}1&{\mbox{n}}{\acute {{\hat {{\mbox{e}}}}}}{\mbox{u}}\ x<0\\x+a&{\mbox{n}}{\acute {{\hat {{\mbox{e}}}}}}{\mbox{u}}\ x\geq 0.\end{cases}}$

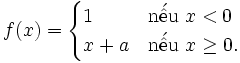
Phải chọn a bằng bao nhiêu để f(x) liên tục tại điểm x = 0?

4) Hoạt động ngôn ngữ: Phân biệt các khái niệm: liên tục, liên tục bên trái, liên tục bên phải, liên tục trên một đoạn, khoảng, gián đoạn.

Tài liệu tham khảo

• Giáo trình PPDH môn Toán, phần đại cương, Trần Khánh Hưng, Nhà xuất bản giáo dục, 1997, trang 55.
• Giáo trình PPDH môn Toán, phần đại cương, Nguyễn Bá Kim, Vũ Dương Thụy, Nhà xuất bản giáo dục, 2000, 76. (khai thác chưa hết)

Bài liên quan

• Phân bậc hoạt động
• Hướng đích và gợi động cơ
• Những thành tố cơ sở của phương pháp dạy học toán
• Tri thức và tri thức phương pháp

Liên kết đến đây

• Những thành tố cơ sở của phương pháp dạy học toán