Rèn luyện cho học sinh kĩ năng học tập môn Toán
Trong tâm lý - giáo dục, người ta thường chia kĩ năng học tập cơ bản thành bốn nhóm: kĩ năng nhận thức, kĩ năng thực hành, kĩ năng tổ chức hoạt động nhận thức và kĩ năng tự kiểm tra, đánh giá.
I. Kĩ năng nhận thức[sửa]
Nhóm kĩ năng nhận thức trong môn Toán bao gồm: kĩ năng nắm vững khái niệm, định lí, quy tắc và dự đoán và suy đoán.
1) Kĩ năng nắm vững khái niệm[sửa]
Rèn luyện cho học sinh hiểu được các dấu hiệu đặc trưng của một khái niệm, từ đó biết nhận dạng một khái niệm, tức là biết phát hiện xem một đối tượng cho trước có thuộc phạm vi khái niệm nào đó không, đồng thời biết thể hiện khái niệm, nghĩa là biết tạo ra một đối tượng thuộc phạm vi một khái niệm cho trước. Trên cơ sở đó, học sinh có thể hiểu được quan hệ giữa các khái niệm, chẳng hạn hiểu được "hình hộp chữ nhật" và "hình lăng trụ đứng có đáy là hình chữ nhật" là như nhau.
- Xem chi tiết: Dạy học khái niệm toán học
2) Kĩ năng nắm vững định lí[sửa]
Nắm vững một định lí là phân biết được phần giả thiết và phần kết luận của định lí đó, có thể nếu cách phát biểu khác của định lí, hiểu được mối liên hệ logic giữa các định lí.
- Xem chi tiết: Dạy học định lí toán học
3) Kĩ năng vận dụng các quy tắc[sửa]
Một khía cạnh khác của kĩ năng nhận thức trong môn toán là kĩ năng áp dụng thành thạo mỗi quy tắc, trong đó yêu cầu vận dụng linh hoạt, tránh máy móc. Chẳng hạn quy tắc hình bình hành để xác định tổng của hai vecto, quy tắc xác định ảnh của một điểm qua phép vị tự,... quy tắc giải và biện luận hệ hai phương trình bậc nhất hai ẩn,...
Giáo
viên
cần
chú
ý
lựa
chọn,
khai
thác
những
ví
dụ,
những
bài
tập
có
cách
giải
quyết
linh
hoạt,
đơn
giản
hơn
là
áp
dụng
quy
tắc
tổng
quát
nhằm
khắc
phục
tính
ý
của
tư
duy
và
rèn
luyện
tính
linh
hoạt
của
trí
tuệ.
Chẳng
hạn,
khi
giải
phương
trình
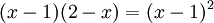 ,
có
học
sinh
khai
triển
phép
tính
ở
cả
hai
vế
nhằm
đưa
về
dạng
phương
trình
bậc
hai
tổng
quát
rồi
áp
dụng
công
thức
nghiệm
mà
không
thấy
đặc
điểm
riêng
của
phương
trình
này
để
có
thể
đưa
ngay
về
phương
trình
tích
(x
-
1)(3
-
2x)
=
0,
từ
đó
suy
ra
được
nghiệm
x
=
1
và
x
=
3/2.
,
có
học
sinh
khai
triển
phép
tính
ở
cả
hai
vế
nhằm
đưa
về
dạng
phương
trình
bậc
hai
tổng
quát
rồi
áp
dụng
công
thức
nghiệm
mà
không
thấy
đặc
điểm
riêng
của
phương
trình
này
để
có
thể
đưa
ngay
về
phương
trình
tích
(x
-
1)(3
-
2x)
=
0,
từ
đó
suy
ra
được
nghiệm
x
=
1
và
x
=
3/2.
Mặt
khác,
cũng
cần
chú
ý
luyện
tập
cho
học
sinh
không
thực
hiện
phép
tương
tự
mà
cách
không
kiểm
tra
khi
chuyển
từ
loại
đối
tượng
này
sang
loại
đối
tượng
khác.
Ví
dụ,
sự
"vận
dụng"
quy
tắc
so
sánh
hai
phân
số
có
cùng
mẫu
số
để
giải
bất
phương
trình
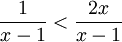 bằng
cách
suy
ra
1
<
2x
là
sai.
bằng
cách
suy
ra
1
<
2x
là
sai.
- Xem chi tiết: Dạy học tri thức phương pháp
4) Kĩ năng dự đoán và suy đoán[sửa]
Để rèn luyện cho học sinh khả năng tìm tòi, dự đoán được những tính chất, những quy luận của hiện thực khách quan, tự mình phát hiện và phát biể vấn đề, cần phải luyện tập cho học sinh kĩ năng dự đoán và suy đoán (thông qua quan sát, so sánh, đặc biệt hóa, khái quát hóa, tương tự,...).
Chẳng
hạn,
xét
bài
toán
"Chứng
minh
rằng
nếu
các
góc
của
tam
giác
ABC
thỏa
mãn
hệ
thức
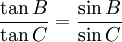 thì
tam
giác
ABC
vuông
hoặc
cân".
Xuất
phát
từ
chỗ
quan
sát
thấy
vai
trò
của
các
góc
B
và
C
bình
đẳng
với
nhau
trong
đẳng
thức
đã
cho,
ta
có
thể
dự
đoán
rằng:
nếu
tam
giác
ABC
là
tam
giác
cân
thì
B
=
C;
còn
nếu
tam
giác
ABC
vuông
thì
phải
vuông
ở
A,
bởi
vì,
nếu
vuông
ở
B
thì
do
vai
trò
của
B
và
C
như
nhau,
cũng
sẽ
vuông
ở
C,
đó
là
điều
vô
lí.
Như
vậy,
ta
đã
định
hướng
mục
tiêu
của
phép
chứng
minh
là
B
=
C
hoặc
A
=
90°.
thì
tam
giác
ABC
vuông
hoặc
cân".
Xuất
phát
từ
chỗ
quan
sát
thấy
vai
trò
của
các
góc
B
và
C
bình
đẳng
với
nhau
trong
đẳng
thức
đã
cho,
ta
có
thể
dự
đoán
rằng:
nếu
tam
giác
ABC
là
tam
giác
cân
thì
B
=
C;
còn
nếu
tam
giác
ABC
vuông
thì
phải
vuông
ở
A,
bởi
vì,
nếu
vuông
ở
B
thì
do
vai
trò
của
B
và
C
như
nhau,
cũng
sẽ
vuông
ở
C,
đó
là
điều
vô
lí.
Như
vậy,
ta
đã
định
hướng
mục
tiêu
của
phép
chứng
minh
là
B
=
C
hoặc
A
=
90°.
Một
ví
dụ
khác,
xét
bài
toán
"Cho
tam
giác
ABC
thỏa
mãn
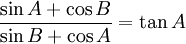 .
Chứng
minh
rằng
tam
giác
ABC
vuông".
Quan
sát
vế
phải
của
đẳng
thức
đã
cho
dự
đoán
rằng
tam
giác
không
thể
vuông
tại
A,
vì
nếu
vuông
ở
A
thì
cos
A
=
0
và
đẳng
thức
đã
cho
vô
nghĩa.
Còn
nếu
vuông
ở
B
thì
cos
B
=
0
và
sin
B
=
1,
khi
đó
đẳng
thức
đã
cho
trở
thành
.
Chứng
minh
rằng
tam
giác
ABC
vuông".
Quan
sát
vế
phải
của
đẳng
thức
đã
cho
dự
đoán
rằng
tam
giác
không
thể
vuông
tại
A,
vì
nếu
vuông
ở
A
thì
cos
A
=
0
và
đẳng
thức
đã
cho
vô
nghĩa.
Còn
nếu
vuông
ở
B
thì
cos
B
=
0
và
sin
B
=
1,
khi
đó
đẳng
thức
đã
cho
trở
thành
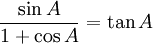 ,
vô
lí.
Như
vậy,
ta
đã
định
hướng
được
mục
tiêu
của
phép
chứng
minh
là
C
=
90°.
,
vô
lí.
Như
vậy,
ta
đã
định
hướng
được
mục
tiêu
của
phép
chứng
minh
là
C
=
90°.
II. Kĩ năng thực hành[sửa]
Kĩ năng thực hành trong môn Toán bao gồm kĩ năng vận dụng tri thức vào hoạt động giải toán, kĩ năng toán học hóa tình huống thực tiễn (trong bài toán hoặc trong đời sống).
1) Hoạt động giải toán[sửa]
Hoạt động giải toán có thể xem là hình thức chủ yếu của hoạt động toán học đối với học sinh. Nó là điều kiện để thực hiện tốt các mục đích của việc dạy học môn toán ở trường phổ thông. Kĩ năng vận dụng tri thức một cách có hiệu quả vào hoạt động giải toán của học sinh được huấn luyện trong quá trình học tìm tòi lời giải của bài toán. Quá trình này thường được tiến hành theo bốn bước: tìm hiểu nội dung bài toán, xây dựng chương trình giải, thực hiện chương trình giải, kiểm tra và nghiên cứu lời giải tìm được. (xem chi tiết)
Trong hoạt động giải toán, cần chú ý rèn luyện cho học sinh kĩ năng chuyển từ tư duy thuận sang tư duy nghịch, đó là điều kiện quan trọng để nắm vững và vận dụng kiến thức, một thành phân của tư duy toán học.
Chẳng
hạn,
học
sinh
thường
hiểu
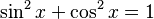 với
mọi
x
và
dễ
dàng
áp
dụng
nó
để
giản
ước
các
biểu
thức
lượng
giác.
Nhưng,
khi
gặp
phương
trình
với
mọi
x
và
dễ
dàng
áp
dụng
nó
để
giản
ước
các
biểu
thức
lượng
giác.
Nhưng,
khi
gặp
phương
trình
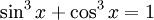 thì
không
mấy
em
nghĩ
được
cách
thay
hằng
số
1
ở
vế
phải
bằng
thì
không
mấy
em
nghĩ
được
cách
thay
hằng
số
1
ở
vế
phải
bằng
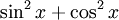 để
sau
đó
nhóm
lại
rồi
biện
luận
và
đi
đến
một
cách
giải.
để
sau
đó
nhóm
lại
rồi
biện
luận
và
đi
đến
một
cách
giải.
Trong dạy học, cần chú ý rèn cho học sinh kĩ năng biến đổi xuôi chiều và ngược chiều song song với nhau, giúp cho việc hình thành các liên tưởng ngược diễn ra đồng thời với việc hình thành liên tưởng thuận.
Chẳng
hạn,
học
sinh
được
học
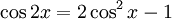 ,
,
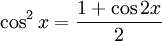 và
áp
dụng
nó
dễ
dàng
để
giải
toán.
Nhưng,
khi
gặp
biểu
thức
có
chứa
và
áp
dụng
nó
dễ
dàng
để
giải
toán.
Nhưng,
khi
gặp
biểu
thức
có
chứa
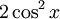 thì
không
mấy
học
sinh
thay
bằng
thì
không
mấy
học
sinh
thay
bằng
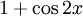 mà
thường
thay
bằng
mà
thường
thay
bằng
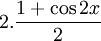 rồi
rút
gọn!
rồi
rút
gọn!
Hay
học
sinh
đều
biết
định
lí
co-si
cho
hai
số
không
âm
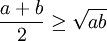 ,
nhưng
khi
gặp
biểu
thức
4ab
thì
ít
học
sinh
nghĩ
đến
việc
áp
dụng
,
nhưng
khi
gặp
biểu
thức
4ab
thì
ít
học
sinh
nghĩ
đến
việc
áp
dụng
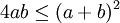
Xét
một
ví
dụ
khác,
học
sinh
được
học
về
đẳng
thức
tam
giác
giữa
các
vecto:
"Với
bất
kì
ba
điểm
A,
B,
C
ta
luôn
có
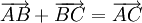 .
Học
sinh
vận
dụng
một
cách
không
khó
khăn
theo
chiều
thuận[1],
chẳng
hạn,
để
tính
tổng
.
Học
sinh
vận
dụng
một
cách
không
khó
khăn
theo
chiều
thuận[1],
chẳng
hạn,
để
tính
tổng
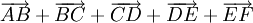 đối
với
đa
giác
ABCDEF.
Nhưng
nếu
giáo
viên
không
chú
ý
rèn
luyện
cho
học
sinh
sử
dụng
đẳng
thức
tam
giác
trên
theo
chiều
ngược[2]
thì
nhiều
học
sinh
sẽ
lúng
túng
khi
giải
bài
toán
"Cho
tứ
giác
ABCD,
chứng
minh
rằng
đối
với
đa
giác
ABCDEF.
Nhưng
nếu
giáo
viên
không
chú
ý
rèn
luyện
cho
học
sinh
sử
dụng
đẳng
thức
tam
giác
trên
theo
chiều
ngược[2]
thì
nhiều
học
sinh
sẽ
lúng
túng
khi
giải
bài
toán
"Cho
tứ
giác
ABCD,
chứng
minh
rằng
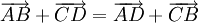 "
bằng
cách
phân
tích
"
bằng
cách
phân
tích
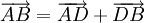 và
và
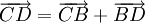 sau
đó
cộng
theo
từng
vế
rồi
giản
ước.
sau
đó
cộng
theo
từng
vế
rồi
giản
ước.
2) Kĩ năng toán học hóa tình huống thực tiễn[sửa]
Kĩ năng toán học hóa các tình huống thực tiễn được cho trong bài toán học nảy sinh từ thực tế đời sống nhằm tạo điều kiện cho học sinh biết vận dụng những kiến thức toán học trong nhà trường vào cuộc sống, góp phần gây hứng thú học tập, giúp học sinh nắm được thực chất nội dung vấn đề và tránh hiểu các sự kiện toán học một cách hình thức.
- Để rèn luyện cho học sinh kĩ năng toán học hóa các tính huống thực tiễn, cần chú ý lựa chọn các bài toán có nội dung thực tế của khoa học, kĩ thuật, của các môn học khác và nhất là thực tế đời sống thường ngày quen thuộc với học sinh.
- Đồng thời nên phát biểu một số bài toán không phải dưới dạng thuần túy toán học mà dưới dạng một vấn đề thực tế phải giải quyết. Ví dụ, bài toán "Cho đường thẳng d và hai điểm A, B cùng nằm trên một mặt phẳng có bờ là d. Hãy tìm trên đường thẳng d một điểm M sao cho tổng khoảng cách MA + MB nhỏ nhất" có thể phát biểu dưới dạng "Hàng ngày bạn An phải đi từ nhà đến bờ sông xách nước để tưới cây cho ruộng rau ở cùng một phía của bờ sông. Hỏi phải chọn vị trí nơi lấy nước tại bờ sông ở chỗ nào để quãng đường đi từ nhà đến ruộng rau là ngắn nhất?"
Để tạo điều kiện vận dụng tri thức vào thực tế, còn phải có những kĩ năng thực hành cần thiết. Đó là các kĩ năng tính toán, vẽ hình, đo đạc.[3]
- Trong hoạt động thực tế ở bất kì lĩnh vực nào cũng đòi hỏi kĩ năng tính toán: tính đúng, tính nhanh, tính hợp lí, cùng với các đức tính cẩn thận, chu đáo, kiên nhẫn. Để rèn luyện cho học sinh các kĩ năng này, cần tránh tình trạng ít ra bài tập đòi hỏi tính toán, cũng như khi dạy giải bài tập chỉ dừng lại ở "phương hướng" mà ngại nỗ lực, làm các phép tính cụ thể để đi đến kết quả cuối cùng.[4] Giáo viên cũng cần thường xuyên khuyến khích học sinh tìm tòi các cách tính toán khác nhau và biết chọn phương án hợp lí nhất, chẳng hạn tăng cường khả năng tính nhẩm[5], rèn luyện kĩ năng tính ước chừng khi học sinh sử dụng máy tính điện tử[6]
- Cần phải luyện tập cho học sinh thói quen vẽ hình cẩn thận, chính xác, theo đúng quy ước và phù hợp với lý thuyết biểu diễn hình học (đặc biệt là vẽ hình trong không gian), chống vẽ ẩu, tùy tiện.
- Khi rèn luyện cho học sinh kĩ năng đo đạc, cần huấn luyện cho học sinh có thói quen ước lượng các độ dài và chiều cao bằng mắt, sử dụng các dụng cụ đo[7]
III. Kĩ năng tổ chức hoạt động nhận thức[sửa]
Việc rèn luyện kĩ năng tổ chức hoạt động nhận thức đòi hỏi học sinh phải có kế hoạch học tập và biết cách học phù hợp với điều kiện và năng lực của bản thân nhằm phấn đều đạt được mục tiêu đặt ra trong từng giai đoạn.
- Mục này còn sơ khai, mời bạn góp một tay.
IV. Kĩ năng tự kiểm tra, đánh giá[sửa]
Hoạt động học của học sinh là quá trình tự vận động để chiếm lĩnh tri thức và người học không chỉ tiếp thu thụ động mà có sự điều chỉnh để đạt kết quả mong muốn. Muốn vậy, học sinh phải có kĩ năng tự kiểm tra, đánh giá để làm căn cứ cho sự "tự điều chỉnh".
Để rèn luyện kĩ năng này, trước hết phải biết xác định rõ mục tiêu học tập của từng giai đoạn[8] hoặc từng phần kiến thức của chương trình[9] đối với bản thân mình.
Với mỗi mục tiêu học tập, căn cứ vào những lần kiểm tra của giáo viên[10] và nhất là căn cứ vào việc tự đánh giá khả năng học tập của bản thân[11] thông qua việc học lý thuyết[12], việc giải từng bài tập.[13] Từ đó thấy được chỗ còn yếu, chỗ thiếu sót của bản thân về những mặt nào đó mà đề ra phương hướng khắc phục[14]
Một khi học sinh đã có kĩ năng tự kiểm tra, đánh giá và biết tự điều chỉnh thì kết quả học tập sẽ được nâng dần lên.
Tài liệu tham khảo[sửa]
- Phương pháp dạy học môn Toán, Nguyễn Bá Kim, Vũ Dương Thụy, NXB Giáo dục, 2000, trang 171
- How to Study Mathematics - (tiếng Anh)
Chú thích[sửa]
- ↑ Chiều thuận: tổng hai của hai vecto nối tiếp
- ↑ Chiều ngược: Phân tích một vecto thành tổng hai vecto nối tiếp
- ↑ Những kĩ năng này không chỉ cần thiết cho việc toán học hóa thực tiễn mà trong chính các hoạt động giải toán cũng rất cần thiết.
- ↑ Tình trạng này có tác hại không nhỏ đối với học sinh trong quá trình học tập hiện tại và trong cuộc sống sau này. Khi giải quyết vấn đề, có đi sâu vào những chi tiết, những tính toán cụ thể mới sáng tỏ nhiều khía cạnh, có khi giúp ta điều chỉnh cả phương hướng ban đầu.
- ↑ Góp phần phát triển óc quan sát, trí nhớ, khả năng chú ý,...
- ↑ Để bước đầu kiểm tra kết quả tính toán sau khi bấm máy,...
- ↑ Các loại thước đo độ dài, eke, thước đo góc,...
- ↑ Từng tháng, từng học kì, từng năm học,...
- ↑ Từng chương, từng chủ đề,...
- ↑ Kiểm tra miệng, kiểm tra viết, kiểm tra vở ghi, vở bài tập,...
- ↑ Có thể nhờ cha mẹ, nhờ bạn bè... kiểm tra giúp
- ↑ Tự đánh giá việc nắm vững khái niệm, định lí
- ↑ Tự đánh giá khả năng vận dụng tri thức vào giải các dạng bài tập: bài tập về tính toán, về chứng minh,... hoặc bài tập cơ bản giáo viên yêu cầu, bài tập làm thêm,...
- ↑ Hỏi lại giáo viên, nhờ bạn bè giảng giải hộ hoặc nhờ người lớn hướng dẫn lại,...


