Dạy học định lí toán học
"Dạy học định lí toán học" là một trong các tình huống điển hình trong dạy học môn Toán. Việc dạy học định lý toán học nhằm cung cấp cho học sinh một hệ thống kiến thức cơ bản của bộ môn, là cơ hội rất thuận lợi để phát triển ở học sinh khả năng suy luận và chứng minh, góp phần phát triển năng lực trí tuệ.
I. Yêu cầu[sửa]
Việc dạy các định lý toán học cần đạt những yêu cầu sau:
- Nắm được nội dung các định lí và những mối liên hệ giữa chúng, từ đó có khả năng vận dụng các định lý vào hoạt động giải toán cũng như vào các ứng dụng khác.
- Làm cho học sinh thấy được sự cần thiết phải chứng minh chặt chẽ, suy luận chính xác[1]
- Phát triển năng lực chứng minh toán học
II. Các con đường dạy học định lí[sửa]
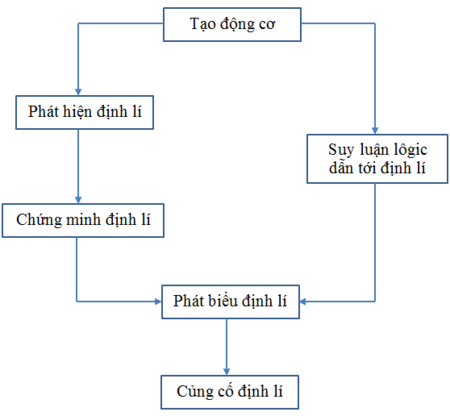
Dạy học định lý toán học có thể thực hiện theo hai con đường: con đường có khâu suy đoán và con đường suy diễn.
- Con đường có khâu suy đoán, bao gồm: tạo động cơ; phát hiện định lí; phát biểu định lý; chứng minh định lý; vận dụng định lý
- Con đường suy diễn, bao gồm: tạo động cơ; suy luận logic dẫn tới định lý; phát biểu định lý; củng cố định lý
Việc dạy học một định lí cụ thể theo con đường nào phụ thuộc vào nội dung định lý và điều kiện cụ thể của học sinh. Ban đầu, ở mức độ thấp[2], dạy học định lý cho học sinh THPT nên theo con đường có khâu suy đoán. Về sau, ở trình độ cao hơn, có thể dạy định lý theo con đường suy diễn.
III. Các hoạt động dạy học định lí[sửa]
1) Chứng minh định lí[sửa]
2) Củng cố định lí[sửa]
Trong quá trình dạy học định lí, giáo viên cần giúp học sinh củng cố kiến thức bằng cách cho họ tập luyện những hoạt động: nhận dạng và thể hiện định lí; hoạt động ngôn ngữ; khái quát hóa, đặc biệt hóa; hệ thống hóa định lí,...
a) Nhận dạng và thể hiện
Nhận dạng một định lí là xem xét một tính huống cho trước có ăn khớp với một định lí nào đó không và thể hiện một định lí là tạo ra một tình huống phù hợp với định lí cho trước.
Ví dụ ...
b) Hoạt động ngôn ngữ
Cần chú trọng phân tích cấu trúc logic cũng như phân tích nội dung định lí, khuyến khích học sinh thay đổi hình thức phát biểu định lí nhằm phát triển năng lực diễn đạt độc lập những ý nghĩ của mình.
Ví dụ, có thể cho học sinh phát biểu định lí "Một đường thẳng a không nằm trên mặt phẳng (P) và song song với một đường thẳng b nằm trong (P) thì đường thẳng a song song với (P)" theo những cách khác nhau:
- Một đường thẳng không nằm trong một mặt phẳng cho trước mà song song với một đường thẳng nằm trong mặt phẳng đã cho thì nó song song với mặt phẳng đó.
- Điều kiện đủ để một đường thẳng song song với một mặt phẳng là nó song song với một đường thẳng nào đó trong mặt phẳng ấy.
- Nếu một mặt phẳng có chứa một đường thẳng song song với một đường thẳng khác không nằm trong nó thì mặt phẳng này song song với đường thẳng ấy
c) Các hoạt động củng cố khác
IV. Trình tự truyền thụ định lí toán học mới[sửa]
Tài liệu tham khảo[sửa]
- Phương pháp dạy học môn Toán, Nguyễn Bá Kim, Vũ Dương Thụy, NXB Giáo dục, 2000, trang 192 - 200
- Tài liệu bồi dưỡng Giáo viên thực hiện chương trình, sách giáo khoa lớp 10 môn Toán, NXB Giáo dục, 2007, trang 101 - 102
- Phương pháp dạy học môn Toán phần hai, Nguyễn Bá Kim, Đinh Nho Chương, Nguyễn Mạnh Cường, Vũ Dương Thụy, Nguyễn Văn Thường, NXB Giáo dục, trang 185 - 191; 312 - 315; 325 - 329
- Tập tin:Phuong-phap-day-hoc-cac-tinh-huong-dien-hinh-trong-mon-Toan-Le-Van-Tien-2005.pdf
Chú thích[sửa]
- ↑ Tất nhiên là ở mức độ phù hợp với trình độ nhận thức của học sinh trung học phổ thông
- ↑ Kiến thức của học sinh còn ít và trình độ nhật thức còn thấp