Sách:Điện từ sinh học/Mô hình nơ ron điện tử
10.1 Giới thiệu chung[sửa]
10.1.1 Mô hình mạch điện tử của các mô có thể kích thích[sửa]
Trong chương 3 và 4, chúng ta đã nói đến các thuộc tính có tính điện của các mô có thể kích thích – dây thần kinh và tế bào cơ. Trong đó, chúng ta đã sử dụng các công thức để mô tả các mạch điện tương đương của màng tế bào cũng như là sử dụng các mạch điện tử thụ động để biểu diễn các thông số của mô. Từ các công thức đó và các mạch điện tử, chúng ta có các công thức sau:
1. Công thức Nernst (Công thức 3.21), công thức này biểu diễn điện áp màng tế bào yêu cầu để làm cân bằng thông lượng ion truyền qua màng tế bào với các tỉ lệ nồng độ tồn tại thực của các loại ion khác nhau. Bởi vì công thức Nernst đánh giá được lực chuyển dời ion do gradient nồng độ coi như là hiệu điện thế [V], nên nó có thể được biểu diễn trong mạch điện tương đương như là một pin.
2. Mô hình cáp của sợi trục thần kinh, bao gồm các điện trở bên ngoài và bên trong cũng như các thông số điện của màng tế bào. Mạch tương đương có thể sử dụng để tính toán cho các công thức cáp tổng quát của sợi dây thần kinh, mô tả các đáp ứng điện áp truyền màng tế bào với các kích thích dòng điện cố định. (Công thức 3.45). Các công thức biến đổi theo thời gian mô tả phản ứng của điện áp màng tế bào do các kích thích xung rời rạc cũng là một phần đáng quan tâm. Điều này được mô tả trong hình 3.11. Mạch điện tương đương đối với công thức dẫn suất của công thức cường độ - thời gian, công thức 3.58 được biểu thị trên hình 3.12.
3. Các mạch điện tương đương mô tả các phản ứng của sợi thần kinh, dưới các điều kiện truyền xung thần kinh hay dưới các điều kiện kẹp điện áp hoặc kẹp không gian, được thể hiện trên hình 4.1, 4.2, và 4.3; tương ứng với các công thức 4.1, 4.2, và 4.3.
4. Mạch điện tử cho các mô hình dẫn song song của màng tế bào, bao gồm các đường dẫn cho Na, K và các ion Cl được mô tả trên hình 4.10, và được thể hiện trong công thức 4.10. Công thức này gồm các thành phần điện thụ động: điện dung màng tế bào, điện thế Nernst đối với Na, K, và Cl cũng như là độ dẫn dò. Xa hơn, mạch điện gồm các phần tử tích cực, độ dẫn Na, K, khi đó được mô tả bởi công thức Hodgkin-Huxley (công thức 4.12-4.24).
Do đó, những hiểu biết của chúng ta về phản ứng điện của các mô có thể kích thích được và các phương pháp mô tả gắn chặt với các khái niệm về mạch điện tử và tới các công thức biểu diễn các phản ứng của chúng. Từ các điểm chuẩn này, người ta có thể tiến hành các phương pháp nhận biết các mạch điện tử tương đương về mặt vật lý cho các mô có khả năng kích thích. Việc nhận biết bản chất vật lý của các mạch điện tử tương đương của các mô có khả năng kích thích có hai mục đích:
1. Nó cho chúng ta cơ hội để xác minh lại các mô hình mà chúng ta đã xây dựng có phản ứng thực sự giống với mô có khả năng kích thích không, cái mà chúng ta quan tâm và đó chính là các mô hình chính xác. Nếu trong trường hợp phản úng của mô hình không chính xác thì chúng ta có thể điều chỉnh lại các thông số để cải thiện và nâng cấp các hiểu biết chính xác mà chúng ta có được về các mô có khả năng kích thích. Việc phân tích các phản ứng của mô có khả năng kích thích là một mục đích tổng quát nhất của các công việc liên quan tới việc xây dựng mô hình.
2. Tại đây cũng tồn tại khả năng xây dựng hoặc tổng hợp các mạch điện tử mà các phản ứng của nó tương tự như mô thần kinh và nó cũng thực hiện xử lý thông tin tương tự như quá trình xử lý thông tin thực tế đang diễn ra. Trong hầu hết các dạng mô hình tiên tiến thì nó được gọi là quá trình tính toán nơron.
Ở mục 7.3 chúng ta đã đề cập đến khái niệm mô hình một cách tổng quát. Các mô hình khác nhau đã được đưa ra ở Miller (1992). Trong chương này, chúng ta đặc biệt nhắc đến mô hình noron điện tử, triển khai các ví dụ của mô hình để chỉ ra các thuộc tính điện của noron tế bào thần kinh. Các mô hình nơron điện tử dễ hiểu hơn đã được xây dựng từ các thành phần điện tử riêng rẽ có lẽ được tìm ra tại Malmivuo (1973) và Reiss (1964).
Chúng ta chú ý rằng sự minh họa của các mạch điện tử cùng với các bộ tính toán số là một cách khác để nghiên cứu các phản ứng của các mô hình điện tử. Mặc dù trong thực tế thì mô hình nơron thần kinh là một vấn đề rất quan trọng bởi vì nó là cầu nối để xây dựng các mạch điện tử và nó cũng lại là các thành phần của máy tính nơron.
10.1.2 Các máy tính nơron[sửa]
Ứng dụng quan trọng nhất của mô hình nơron điện tử là máy tính nơron. Mặc dù chủ đề này không nằm trong phạm vi của cuốn sách này và các lý thuyết về mạng nơron và máy tính nơron, chúng ta chỉ mô tả một cách tóm tắt và đưa ra một số tham khảo cho chủ đề này mà thôi. Ở Hecht-Nielsen (1988), người ta đã giới thiệu ngắn gọn và súc tích về nó.
Trong các máy tính noron thế hệ đầu tiên thì chúng được gọi là bộ não điện tử. Tại thời điểm đó, khoa học công nghệ phát triển một cách mạnh mẽ đã làm cho các bộ não điện tử này càng ngày càng tiến bộ rất nhanh và đi kèm với nó là một hệ thống lý thuyết có liên quan chính là trí tuệ nhân tạo. Bằng cách sử dụng lý thuyết nghiên cứu về trí tuệ nhân tạo, người ta đã tạo ra các hệ thống chuyên nhiệm rất hữu ích, các chương trình tính toán và hiện nay trên thế giới chì còn vài hạn chế là tốc độ xử lý và các hệ thống nhận biết đánh giá các thông số thông minh mà thôi. Người ta đã đưa ra các tiêu chí về trí tuệ nhân tạo để nhận biết nó rõ hơn từ cách đây 30 năm.
Nếu chúng ta xây dựng được một bộ não điện tử thì nó phải có khả năng học hỏi giống như bộ não sinh học và bắt chước tự nhiên. Các não thật, mặc dù ở mức thô sơ nhưng cũng có cấu trúc rất phức tạp. Não người có khoảng 10^11 nơron, mỗi noron có khả năng lưu trữ hơn 1 bit dữ liệu.
Máy tính ngày càng có bộ nhớ lớn, thoải mái hơn. Trong khi, thời gian thực hiện chương trình máy tính cỡ nano giây thì động vật có vú xử lý thông tin cỡ mili giây. Tuy nhiên tốc độ này thua xa hệ thần kinh người với cấu trúc song song lớn, ở đó, từng nơron xử lý thông tin và có số lượng rất lớn kết nối tới nơron khác. Ngày nay, người ta đang tạo ra những máy tính đa xử lý, nhưng để cho chúng hoạt động hiệu quả như mong đợi, chúng ta cần hàng nghìn vi xử lý hoạt động, đây vẫn là thách thức lớn đối với khoa học máy tính.
10.2 Phân loại các mô hình nơron[sửa]
Nói chung, các mô hình nơron có thể được chia ra thành các loại, tuỳ theo các tiêu chuẩn đánh giá và phân loại cụ thể. Trong phần sau đây, chúng ta sẽ chủ yếu dựa trên 4 tiêu chí phân loại như sau (Malmivuo, 1973):
1. Cấu trúc mô hình có thể biểu diễn thông qua:
a. Các công thức toán học (công thức Hodgkin-Huxley, Mục 4.4)
b. Các cấu trúc mô phỏng theo các định luật về vật lý (mô hình Eccles, mục 3.5.4, hình. 3.2)
c. Các cấu trúc khác về mặt vật lý nhưng lại tương tự các hiện tượng tự nhiên , minh họa các chức năng tự nhiên của nó (mô hình nơron điện tử)
2.
Các
mô
hình
có
thể
mô
tả
một
hiện
tượng
khác
với
các
mảng
khái
niệm:
Cấu trúc (thông thường được mô tả bằng các mô hình cơ khí)
a. Hàm chức năng (thường được mô tả bằng các mô hình máy tính, toán học và mạch điện tử)
b. Sự tiến triển
c. Vị trí trong hệ thống phân cấp
3.
Phân
chia
theo
mức
độ
hiện
tượng
vật
lý:
- Mức độ trong noron
(a)Màng tế bào ở trạng thái nghỉ
(b) Cấu trúc tạo nên xung thần kinh
(c) Quá trình truyền xung thần kinh trong sợi thần kinh
- Các chức năng đáp ứng và kích thích của các nơron đơn lẻ
(a)
Các
chức
năng
đáp
ứng
và
kích
thích
của
các
nơron
đơn
lẻ
(b) Quá trình truyền của kỳ tiếp hợp
(c) Tương tác giữa các nơron và các nhóm nơron, các mạng nơron
(d). Mức độ tâm sinh lý
4.
Phân
chi
theo
các
thông
số
mô
hình.
Các
biến
bao
gồm
trong
các
hệ
thống
khác
nhau
có
các
hằng
số
thời
gian
khác
nhau.
Dựa
trên
cơ
sở
các
phân
chia
này
chúng
ta
thu
được:
a. Các thông số nghỉ
b. Các thông số kích thích
c. Các thông số khôi phục
d. Các thông số điều chỉnh
Phần này sẽ quan tâm đến các ví dụ về mô hình nơron điện tử mà nó mô tả quá trình tạo ra của các xung hoạt động, các nơron được coi là các đơn vị độc lập và quá trình truyền xung thần kinh trong sợi thần kinh.
10.3 Các mô hình mô tả hàm biểu diễn của màng tế bào[sửa]
Hầu hết các mô hình miêu tả cấu trúc kích thích của màng tế bào là các mô hình nhận biết điện tử của màng tế bào theo lý thuyết Hodgkin – Huxley (Hodgkin and Huxley, 1952). Trong phần sau, chúng ta sẽ có hai mô hình được quan tâm.
10.3.1 Mô hình màng tế bào của Lewis[sửa]
Edwin R. Lewis đã đưa ra một vài mô hình điện tử mà chúng chủ yếu dựa theo các công thức của Hodgkin – Huxley. Các độ dẫn Na, K, các liên kết kỳ tiếp hợp và các chức năng khác của mô hình được xây dựng với các transitors rời rạc và cách linh kiện kết hợp khác. Tất cả mạch điện trên đều là các mạch mắc song song giữa các nút đặc trưng cho các phần bên trong và bên ngoài màng tế bào.
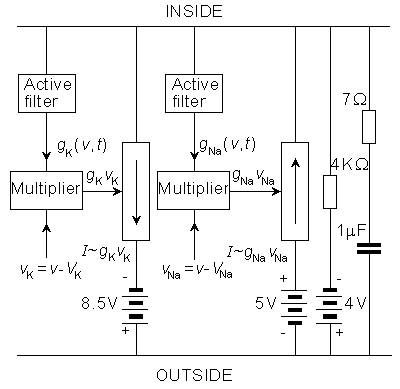
Chúng ta sẽ xem xét mô hình mà Lewis đưa ra năm 1964. Lewis đã chỉ ra độ dẫn Na và K sử dụng phần cứng điện tử với bộ lọc tích cực, được thể hiện trên sơ đồ khối hình 10.1. Do đầu ra của mô hình là điện áp truyền màng tế bào Vm nên dòng điện của các ion K có thể tính được bằng cách nhân điện áp tương ứng Gk với (Vm - VK). Hình 10.1 là một mô hình tương đương vật lý chính xác của công thức Hodgkin – Huxley và đáp ứng đầu ra của điện áp Vm của đầu ra tương ứng mà nó mô tả các công thức Hodgkin – Huxley.
Mạch điện tử trong mạng noron thần kinh Lewis (Lewis neuromime) cung cấp để chèn (và thay đổi) không chỉ với các hằng số GK max, GNa max, VK, VNa, VCl, là những hằng số tạo nên công thức Hodgkin-Huxley, mà còn có τh, τm, τn, cho phép điều chỉnh công thức Hodgkin-Huxley. Mục đích nghiên cứu của Lewis là mô phỏng đặc tính mạng nơron thần kinh, bao gồm các noron ghép, mà mỗi noron được mô phỏng bởi một neuromime, sẽ được đưa ra ở phần sau trong chương này.
Để nhận biết được về mặt điện tử thì các điện áp màng tế bào được nhân với 100 để cung cấp cho mạch điện tử. Trong các giá trị định lượng khác thì các giá trị ban đầu của màng tế bào sinh học được sử dụng. Tiếp theo sau đó thì các thành phần của mô hình sẽ được phân tích riêng rẽ
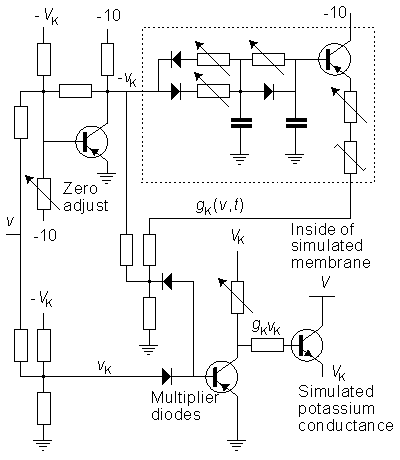
Độ dẫn điện của K
Mạch điện mô phỏng độ dẫn của các ion K+ được chỉ ra trên hình 10.2. Hàm dẫn điện GK(Vm,t) được tạo ra từ điện áp màng tế bào mô phỏng thông qua các bộ lọc tích cực phi tuyến theo như mô hình Hodgin-Huxley. Tại đây có 3 biến trở trong bộ lọc cung cấp quá trình điều khiển trong suốt thời gian trễ, thời gian tăng và thời gian giảm. Các giá trị độ dẫn của K được điều chỉnh cùng với các thiết bị đo điện thế mà nó là bộ điều chỉnh biên độ của bộ nhân. Mạch nhân tạo ra hàm GK(Vm,t)•vK, với vK là giá trị chênh lệch điện thế kênh K (VK) và (Vm) là điện thế nghỉ màng tế bào. Bộ nhân này dựa trên hàm số bình phương của hai diot.
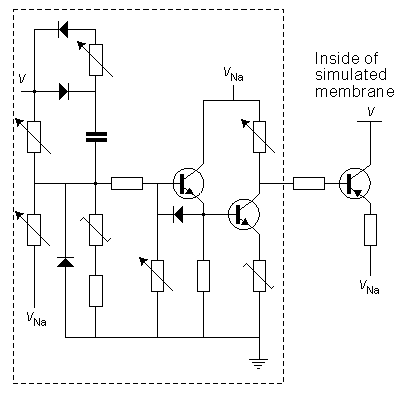
Độ dẫn điện của Na
Trong mạch điện mô phỏng độ dẫn Na, Lewis đã bỏ qua bộ nhân trên cơ sở điện áp cân bằng của các ion Na+ là khoảng 120mV so với điện áp nghỉ. Do chúng ta quan tâm tới sự thay đổi nhỏ của điện áp màng tế bào nên sự thay đổi nồng độ ion Na+ có thể coi là bằng hằng số như được chỉ ra trên hình 10.3. Hằng số thời gian của quá trình khử hoạt tính được định nghĩa theo các biến trở (varistor). Quá trình khử hoạt tính giảm một cách đều đều với quá trình khử cực, giảm xấp xỉ như trong mô hình Hodgkin-Huxley.
Xung hoạt động được kích thích
Thông qua việc kết nối với các thành phần của mô hình màng tế bào như trong hình 10.4 và thông qua quá trình kích thích một mô hình tuơng tự như sợi dây thần kinh thực sự thì mô hình tạo ra một xung hoạt động màng tế bào. Xung hoạt động được mô phỏng này được thực hiện giống xung hoạt động thực rất chính xác. Hình 10.5A miêu tả xung kích hoạt đơn được tạo ra bởi mô hình màng tế bào Lewis và hình 10.5B chỉ ra chuỗi các xung hoạt động.
10.3.2 Mô hình màng tế bào của Roy[sửa]
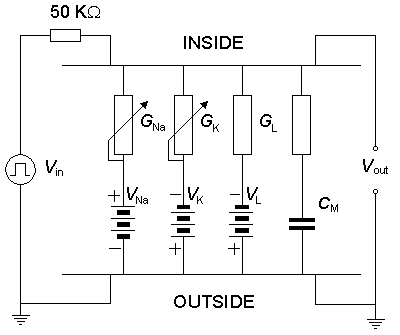
Guy Roy đã công bố mô hình màng tế bào điện tử của mình vào năm 1972 (Roy, 1972) và đặt cho nó cái tên là "Neurofet." Mô hình của ông, tương tự như của Lewis là đều dựa trên mô hình Hodgkin-Huxley. Roy sử dụng các transistor trường FET để mô phỏng các độ dẫn Na và K. Các transistor trường FET được biết đến như là các bộ dẫn có thể điều chỉnh được. Do đó các mạch nhân của Lewis có thể được kết hợp với các phần tử FET đơn lẻ (xem hình 10.6).
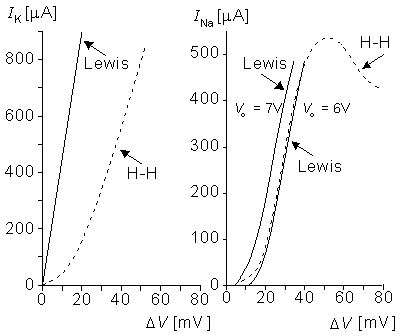
Trong mô hình của Roy thì độ dẫn được điều khiển bởi các mạch bao gồm các mạch khuyếch đại, các tụ điện và các điện trở. Mạch này được thiết kế để tạo ra độ dẫn tác động tương đương như mô hình Hodgkin-Huxley. Mục đích chính của Roy là nhằm đạt được một mô hình đơn giản hơn để mô phỏng một cách chính xác mô hình Hodgkin-Huxley. Tuy thế, nhưng các kết quả đo được từ mô hình của chúng, như được chỉ ra trên hình 10.7 và 10.8, cũng khá gần với các kết quả thu đuợc của Hodgkin-Huxley.
Hình 10.7 mô tả các giá trị trạng thái ổn định đối với các độ dẫn Na và K như một hàm số của điện áp cung cấp. Chú ý rằng đối với độ d K thì giá trị được chỉ ra ở trạng thái ổn định. Đối với Na thì các gía trị mô tả chính là bằng ; đó là giá trị mà độ dẫn Na có thể thu nhân được như h duy trì tại mức độ nghỉ của nó (h0). (Giá trị độ dẫn điện của Na và K của Hodgkin và Huxley từ tương ứng bảng 1 và 2, 1952).
Mô hình màng tế bào đầy đủ thu được thông qua việc kết nối các độ dẫn Na và K nối tiếp với nguồn điện tương ứng và điện dung của màng tế bào mô phỏng với giá trị tụ điện bằng 4.7 nF và mộ độ dẫn dòng rò với điện trở có giá trị bằng 200 Ωk . Kết quả của trình mô phỏng xung hoạt động được miêu tả trên hình 10.8
10.4 Các mô hình mô tả tế bào là một đơn vị độc lập[sửa]
10.4.1 Mô hình nơron của Lewis[sửa]
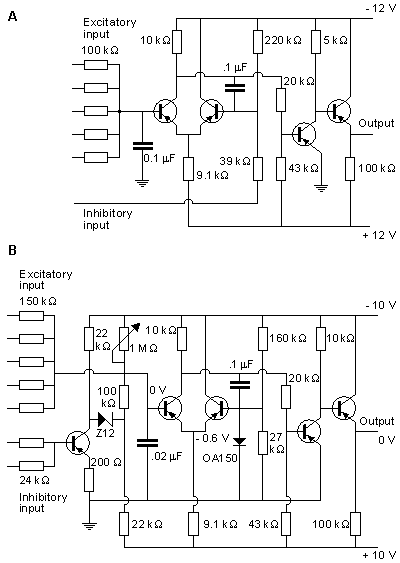
Trong chương này, mô hình nơron được Lewis miêu tả vào năm 1968 (Lewis, 1968) sẽ được trình bày một cách ngắn gọn. Mô hình Lewis dựa trên mô hình màng tế bào của Hodgkin-Huxley và các lý thuyết của Eccles (Eccles, 1964) về quá trình truyền đạt tại kỳ tiếp hợp. Mô hình mạch điện được mô tả trên hình 10.9
Mô hình nơron được chia thành hai phần: Phần ký tiếp hợp và phần tạo xung hoạt động. Cả hai phần này đều bao gồm các mạch điện song song được liên kết với các nút đặc trưng cho các vị trí của tế bào bên trong và tế bào bên ngoài của màng tế bào.
Phần đặc trưng cho khơp nối tại kỳ tiếp hợp được chia thành hai phần. Một trong số chúng đặc trưng cho tiếp nối hạn chế kích thích và tiếp nối kích thích khác. Việc cảm nhận của phần này tạo ra tại tiếp nối kỳ tiếp hợp kích thích bị làm giảm bởi điện áp được chỉ ra tại các tiếp nối hạn chế kích thích. Phần tạo ra xung hoạt động là dựa trên mô hình Hodgkin-Huxley. Như được mô tả trước đây, nó bao gồm các mạch thông thường mô phỏng độ dẫn của Na và K, độ dẫn dòng rò và điện dung màng tế bào. Mạch điện cũng bao gồm bộ khuếch đại cho tín hiệu đầu ra.
Mô hình nơron có mối quan hệ rất phức tạp là nhằm để sử dụng trong nghiên cứu mạng nơron. Tuy nhiên, nó thực tế là một phiên bản đã được đơn giản hoá của Lewis bằng một mạng gồm 46 điện trở cùng loại. Mục đích của việc làm đơn giản hoá mô hình Lewis là nhằm mô phỏng dạng xung kích hoạt mà không mang đến một độ chính xác cao nhất mà chỉ đi cùng với một độ chính xác nhất định của một mô hình đơn giản mà thôi. Hình 10.10, 10.11 và 10.12 chỉ ra các đáp ứng của mô hình được so sánh với các giá trị mô phỏng dựa vào trực tiếp mô hình Hodgkin-Huxley.
Từ hình 10.10, chúng ta thấy rằng khi dòng kích thích bắt đầu được kích hoạt thì dòng chuyển dời của các ion Na+ được xác định bởi Lewis tăng lên tới giá trị đỉnh hầu như ngay lập tức, trong khi dòng ion Na+ của sợi dây thần kinh sinh học Hodgkin-Huxley tăng chậm hơn nhiều. Chu kỳ phân rã của dòng điện này xuất hiện tại một tốc độ gần như thế trong cả hai trường hợp. Đáp ứng của dòng ion K+ rất giống nhau trong cả hai mô hình và màng tế bào sinh học mà nó được mô phỏng bởi Hodgkin-Huxley.
Hình 10.11A và 10.11B so sánh các dòng ion Na+ và K+ của mô hình Lewis với mô hình của Hodgkin-Huxley. Hình 10.12 mô tả xung kích hoạt được tạo ra bởi mô hình Lewis. Biên độ đỉnh của dòng Na+ mô phỏng là bằng 10mA. Biên độ này xấp xỉ 450 µA/cm2 trong màng tế bào và nó bằng một nửa gía trị tính được trong mô hình Hodgkin-Huxley. Dòng chuyển dời của các ion K+ cực đại trong mạch là 3mA tương ứng với 135 µA/cm2 trong màng tế bào. Tác giả đã đưa ra mà không điều chỉnh về điện thế nghỉ của màng hoặc trục thời gian.
10.4.2 Mô hình nơron của Harmon[sửa]
Quá trình thực hiện mạch điện tử của mô hình Hodgkin-Huxley là rất chính xác trong việc mô phỏng hàm số của một nơron đơn lẻ. Tuy nhiên, khi một ai đó thực hiện việc mô phỏng hàm số mạng nơron thì chúng trở nên vô cùng phức tạp. Rất nhiều nhà khoa học cảm thấy rằng khi mô phỏng một mạng nơron lớn thì cấu trúc bên trong của các phần tử của nó có thể là không quá quan trọng. Nó có thể được thoả mãn một cách đơn giản để đảm bảo rằng các phần tự tạo ra một xung hoạt động tương ứng với các kích thích trong một phần tương tự đối với một nơron thực tế. Dựa trên nguyên tắc này, Leon D. Harmon cấu tạo nên mô hình nơron có một mạch rất đơn giản. Với mô hình này, ông đã thực hiện các thí nghiệm trong đó ông mô phỏng rất nhiều các hàm về thông số của các nơron (Harmon, 1961).
Mạch của mô hình Harnon được chỉ ra trong hình 10.13. Hình 10.13A và 10.13B chỉ ra các phiên bản sơ bộ và đầy đủ của mạch điện tương ứng. Mô hình được cấu tạo với 5 đầu vào kích thích có thể điều chỉnh được. Các mô hình này bao gồm các mạch điốt đặc trưng cho các hàm kỳ tiếp hợp khác nhau. Tín hiệu được đưa tới đầu vào kích thích làm thay đổi giá trị điện áp trên tụ điện mà sau khi đạt tới 1,5V nó cho phép một bộ tạo xung ổn định đơn tạo được thông qua hai transistor T1và T2 nhằm tạo ra xung động. Xung này được khuếch đại bơỉ transistor T3 và T4. Đầu ra của một mô hình nơron có thể điều chỉnh các đầu vào của khoảng 100 mô hình nơron lân cận. Mô hình cơ bản cũng bao gồm đầu vào hạn chế kích thích. Một xung được đưa vào tại đầu vào có ảnh hướng tới quá trình giảm của bộ cảm nhận đầu vào kích thích.
Không cần có mạch ngoài, Harmon đã nghiên cứu thành công 7 thông số của mô hình nơron. Nó được miêu tả trong hình 10.14 và được mô tả ngắn gọn ở dưới đây
Đường cong quan hệ cường độ và thời gian
Mô hình Harmon chỉ ra đường cong quan hệ giữa cường độ - thời gian tương tự như biểu hiện thực của nơron. Trục thời gian là gần đúng nhưng do các thông số điện của các phần mạch nên trục điện áp cao hơn rất nhiều. Ngưỡng điện áp trong mô hình Harmon là khoảng Vth = 1.5 V, như được mô tả trong hình 10.14A.
Quá trình tích luỹ
Do mô hình không có các mạch bên trong được tạo ra sự tích luỹ một cách cụ thể, nên hiện tượng này là mô tả tổng quát bởi đường cong quan hệ cường độ - thời gian mà nó làm sáng tỏ đường cong kích thích – tích luỹ. Xung hoạt động chỉ được tạo ra khi các kích thích đã kết thúc đủ lâu để tạo ra một xung hoạt động.
Biến đổi theo thời gian
Mô hình mô tả các ngưỡng kích thích trong trường hợp các xung kích thích liên tục nhau khi xung đầu tiên rời khỏi trạng thái quá kích thích thì tới xung thứ hai. Hình 10.14B chỉ ra biên độ yêu cầu của hai xung có độ rộng 0,8 ms như là một hàm số theo thời gian của chúng, và một xung khác chỉ ra ngưỡng làm nhỏ với khoảng các xung giảm dần, do đó, chúng ta sẽ có tổng thời gian. Trong tất cả các trường hợp thì biên độ xung giảm từ giá trị yêu cầu đối với các xung hoạt động từ các xung đơn.
Giai đoạn trơ ì (khôi phục kích thích)
Quá trình khôi phục kích thích thông thường của mô hình sau khi xung kích hoạt được chỉ ra trên hình 10.14C. Đường cong này tương tự với đường cong đối với các nơron sinh học. Mô hình nơron khôi phục hoàn toàn trong khoảng thời gian là 1ms – đó chính là thời gian xung xuất hiện tại đầu ra. Chu kỳ khôi phục tương đối bắt đầu sau khi thời gian bắt đầu (t=0) và sau một khoảng thời gian cố định khoảng 1,7ms. Đường cong A nhận được khi các kích thích được cung cấp một tín hiệu tại đầu vào. Đường cong B đặc trưng cho trường hợp khi các kích thích được cung cấp ngay lập tức tới 3 đầu vào (xem hình 10.13).
Xung đầu ra, xung hoạt động
Xung đầu ra tuân theo định luật tất cả hoặc là không và biên độ của nó khá ổn định. Tuy nhiên, độ rộng của nó là một vài mức độ hàm số của tần số xung. Sự phụ thuộc này được đưa ra trong hình 10.14D.
Độ trễ
Trong trường hợp này, độ trễ được coi là khoảng thời gian giữa thời điểm hoạt động của các xung kích thích và xung đầu ra. Nó không có nghĩa là trễ thông thường như chúng ta thường biết đến. Trong mô hình này, trễ làm một hàm số của sự tích hợp tại đầu vào cũng như là điều kiện khôi phục. Đường cong A trong hình 10.14E đặc trưng cho độ trễ khi các kích thích được cung cấp tới một đầu vào và đường cong B là khi các kích thích được cung cấp tới tất cả 5 đầu vào kích thích.
Kích thích lặp
Kích thích được coi là quá trình tạo ra các xung đầu ra với điện áp hằng số tại đầu vào và tần số. Hình 10.14F, đường cong A, chỉ ra tần số của xung đầu ra khi điện áp đầu vào được kết nối với 3 đầu vào và đường cong B là điện áp đầu vào được kết nối với 1 đầu vào. Tần số đầu ra chỉ cho phép đầu vào đối với các đầu vào điện áp cao. Khi đầu vào giảm, xung sẽ biến mất và tần số đầu ra sẽ giảm tương ứng với đầu vào.
Bằng cách mắc với các tụ điện giữa cổng vào và cổng ra của mô hình nơron thì người ta có thể thực hiện các hàm phúc tạp hơn nhiều. Harmon đã thực hiện các thí nghiệm cùng với việc kết hợp rất nhiều mô hình khác nhau. Hơn thế nữa, ông đã nghiên cứu quá trình truyền của xung kích hoạt bằng các mô hình nối tiếp với nhau. Các mô hình nơron này có thể được cung cấp để mô phỏng các mạng nơron khá phức tạp và thậm chí là mô hình tạo dạng sóng của não.
(A) Đường cong quan hệ cường độ và thời gian;
(B) Biến đổi theo thời gian của kích thích;
(C) Khôi phục kích thích;
(D) Độ rộng của xung đầu ra như là một vài mức hàm số của tần số xung;
(E) Trễ giữa bắt đầu của xung kích thích và bắt đầu của xung hoạt động
như là hàm của tần số kích
(F) Thuộc tính của mô hình trong kích thích lặp. Tần sô đầu vào là 700 p/s.
10.5 Các mô hình mô tả quá trình truyền xung kích hoạt[sửa]
Việc sử dụng sự lặp đi lặp lại của phần màng tế bào mô hình nơron của ông thì Lewis đã mô phỏng quá trình truyền xung kích hoạt trong một sơị dây thần kinh chuẩn và thu được các kết quả khá thú vị. Cấu trúc mô hình, được mô tả trên hình 10.15 có thể được coi là bao gồm một mạng của các thành phần màng tế bào cũng như là chuỗi điện trở trục đặc trưng cho các điện trở tế bào bên trong. Tổng của 6 phần tử được mô tả trên hình. Mô hình là một quá trình thực hiện điện tử của mô hình bộ dẫn dây lõi tuyến tính cùng với các màng tế bào hoạt động.
Hình 10.16A và 10.16B mô tả một mô phỏng của quá trình truyền xung hoạt động trong mô hình bao gồm một chuỗi các đơn vị sợi thần kinh nối tiếp như được mô tả trên hình 10.15. Đường cong A đặc trưng cho trường hợp một chuỗi 6 đơn vị nối tiếp còn đường B là một chuỗi tròn gồm 10 đơn vị. Sau đó các tín hiệu sẽ được ghi lại sau từng giây một. Mô hình 6 đơn vị đặc trưng cho phần của xung sợi thần kinh ống 4cm dài và có bán kính bằng 1mm. Hình 10.16A chỉ ra thời gian dẫn của xung kích hoạt từ 3 đơn vị tới 6 đơn vị là 1,4ms. Do mô hình 6 đơn vị đầy đủ tạo nên 5 lần tăng lên của khoảng cách nên tốc độ dẫn của mô hình là khoảng 17m/s. Nó có thể so sánh với tốc độ dẫn thực sự đo được trong sợi thần kinh ống là từ 14-23m/s.
10.6 Thực hiện mạch tích hợp[sửa]
Sự phát triển của kỹ thuật mạch tích hợp đã tạo ra những mô hình nơron điện tử rất lớn (Mahowadd et al., 1992). Điều này làm cho các mô hình nơron điện tử hoặc mạch giống nơron có thể sử dụng như là các phần tử xử lý trong máy tính điện tử, cái mà được gọi là máy tính nơron. Trong phần dưới đây, chúng ta sẽ đưa ra hai ví dụ về vấn đề này.
Stefan Prange (1988, 1990) đã phát triển mô hình nơron điện tử với kỹ thuật mạch tích hợp. Mạch đó bao gồm 1 nơron với 8 synapses. Kích thước của mạch tích hợp là 4.5x5mm2. Chứa khoảng 200NPN và 100PNP transistor, và khoảng 200 trong số đó được sử dụng. Mạch được chế tạo với một lớp kim loại có bề rộng là 12 µm. Bởi mô hình được thực hiện với kỹ thuật mạch tích hợp, nên nó dễ dàng tạo ra số lượng lớn, rất cần để mô phỏng mạng tế bào thần kinh. Những thí nghiệm này, tuy nhiên nó chưa tạo ra được mô hình đó.
Trong năm 1991, Misha Mahowald và Rodney Douglas đã đưa ra mô hình nơron điện tử thực hiện mạch tích hợp (Mahowald và Douglas, 1991). Nó đã được thực hiện với mạch tranzito bán dẫn oxit kim loại bù (CMOS) dùng kỹ thuật tích hợp cỡ lớn (VLSI). Mô hình của họ mô phỏng rất chính xác đỉnh nhọn của noron Neocortical. Năng lượng tiêu tán của mạch là 60 µW và nó chiếm ít hơn 0.1 mm2. Các tác giả ước lượng rằng có khoảng 100-200 nơrons có thể được tạo ra trên một bàn ren 1cm x 1cm.
Tham khảo[sửa]
Eccles JC (1964): The Physiology of Synapses, 316 pp. Springer-Verlag, Berlin.
Harmon LD (1961): Studies with artificial neurons, I: Properties and functions of an artificial neuron. Kybernetik Heft 3(Dez.): 89-101.
Hecht-Nielsen R (1988): Neurocomputing: Picking the human brain. IEEE Spectrum 25:(3(March)) 36-41.
Hodgkin AL, Huxley AF (1952): A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. (Lond.) 117: 500-44.
Lewis ER (1964): An electronic model of the neuron based on the dynamics of potassium and sodium ion fluxes. In Neural Theory and Modelling. Proceedings of the 1962 Ojai Symposium, ed. RF Reiss, HJ Hamilton, LD Harmon, G Hoyle, D Kennedy, O Schmitt, CAG Wiersma, p. 427, Stanford University Press, Stanford.
Lewis ER (1968): Using electronic circuits to model simple neuroelectric interactions. Proc. IEEE 56:(6) 931-49. (Special issue on studies of neural elements and systems).
Mahowald MA, Douglas RJ (1991): A silicon neuron. Nature 354:(December) 515-8.
Mahowald MA, Douglas RJ, LeMoncheck JE, Mead CA (1992): An introduction to silicon neural analogs. Semin. Neurosci. 4: 83-92.
Malmivuo JA (1973): Bioelectric Function of a Neuron and Its Description With Electronic Models, 195 pp. Helsinki Univ. Techn., Dept. El. Eng. (In Finnish)
Prange S (1988): Aufbau eines Neuronenmodells mit hilfe einer analogen, kundenspezifischen Schaltung. Institute of Microelectronics, Techn. Univ. Berlin, Berlin, pp. 87. (Diploma thesis)
Prange S (1990): Emulation of biology-oriented neural networks. In Proc. Int. Conf. On Parallel Processing in Neural Systems and Computers (ICNC), ed. M Eckmiller, Düsseldorf.
Roy G (1972): A simple electronic analog of the squid axon membrane: The neurofet. IEEE Trans. Biomed. Eng. BME-19:(1) 60-3.
Tonk DW, Hopfield JJ (1987): Collective computation in neuronlike circuits. Sci. Am. 257:(6) 62-70.
Sách tham khảo
Aleksander I (ed.) (1989): Neural Computing Architectures, The Design of Brain-Like Machines, 401 pp. The MIT Press, Cambridge, Mass. Andersson JA, Rosenfeld E (eds.) (1988): Neurocomputing: Foundations of Research, 729 pp. MIT Press, Cambridge, Mass.
Grossberg S (ed.) (1988): Neural Networks and Natural Intelligence, 637 pp. MIT Press, Cambridge, Mass.
Hecht-Nielsen R (1990): Neurocomputing, 432 pp. Addison-Wesley Publishing, Reading, Mass.
MacGregor RJ (1987): Neural and Brain Modelling, 643 pp. Academic Press, San Diego.
MacGregor RJ, Lewis ER (1977): Neural Modelling: Electric Signal Processing in the Nervous System, 414 pp. Plenum Press, New York.
Miller KD (1992): The Use of Models in the Neurosciences. Semin. Neurosci. 4:(1) 92. (Special issue).
Reiss RF, Hamilton HJ, Harmon LD, Hoyle G, Kennedy D, Schmitt O, Wiersma CAG (eds.) (1964): Neural Theory and Modelling. Proceedings of the 1962 Ojai Symposium, 427 pp. Stanford University Press, Stanford.
Sejnowski T (ed.) (1989): Neural Computation, MIT Press, Cambridge, Mass.
| trang trước | Mô hình nơ ron điện tử | Trang tiếp |