Sách:Điện từ sinh học/Mô hình nguồn trường

Chương 8: Các mô hình nguồn trường

Giới thiệu

Trong chương này, chúng ta sẽ phát triển các hình thức biểu diễn của các nguồn điện trong cơ sở điện sinh học. Các nguồn này được phát sinh bởi các dòng điện xuyên qua màng tế bào của các tế bào kích thích, các tế bào này có thể là các tế bào thần kinh hay các tế bào cơ. Chúng ta xét các mô dễ bị kích thích bằng những mô hình rất đơn giản - chủ yếu là các sợi trục hình trụ đơn. Nhưng những kết quả hữu ích thu được trong các chương tiếp theo khi xét toàn bộ các cơ quan, mà chúng có thể được xem như là tập hợp của rất nhiều các phần tử ở trên. Chúng ta coi các nguồn điện sinh học được mô tả như một phân bố bề mặt hay khối của 2 loại thành phần nguồn, đó là đơn cực và lưỡng cực. Vì nền tảng quan trọng của nguốn đơn cực và lưỡng cực, trước tiên chúng ta bắt đầu với sự mô tả của các trường được hình thành bởi mỗi thành phần nguồn trên.

Các mô hình nguồn

Đơn cực

Điều kiện đầu:

Nguồn: Đơn cực trong vùng cố định

Bộ dẫn: Vô hạn, thuần nhất

Cấu hình nguồn đơn giản nhấtlà nguồn điểm hay đơn cực. Nếu chúng ta coi một nguồn dòng điểm của đại lượng I_o nằm trong một môi trường dẫn điện đồng chất vô hạn và có độ dẫn σ, thì khi đó các dòng chảy phải đồng đều và hướng tỏa ra. Do đó, đối với một mặt cầu đồng tâm có bán kính bất kì r, mật độ dòng J ngang qua bề mặt này phải đồng đều và sẽ bằng I_o chia đều trên diện tích bề mặt. Đó là:

(8.1)

Bởi vì dòng luôn cùng phương với bán kính nên mật độ dòng được biểu diễn dưới dạng vector là:

(8.2)

Trong đó là vector đơn vị theo hướng bán kính r, có gốc tại nguồn điểm.

Liên quan đến trường dòng điện được xác định bằng công thức 8.2 là một trường điện thế vô hướng Φ. Bởi vì các dòng điện hướng tâm tại mọi vị trí nên tại mỗi vị trí không có sự biến thiên của điện thế dọc theo phương nằm ngang, như vậy điện thế tại những điểm cùng cách điểm nguồn một bán kính r là bằng nhau. Những mặt đẳng thế là các mặt cầu đồng tâm xung quanh nguồn điểm, điện thế giảm dần theo sự tăng lên của giá trị r. Sự biến thiên của điện thế vô hướng tạo ra điện trường :

(8.3)

Theo định luật Ohm,ta có:

(8.4)

Áp dụng công thức 8.3 và 8.4 vào công thức 8.2 ta được:

(8.5)

Để thỏa mãn công thức 8.5, chỉ có thành phần theo phương của r của có thể đáp ứng. Ta có:

(8.6)

Lấy tích phân theo r ta được:

(8.7)

Theo công thức trên ta thấy, Φ là hằng số trên bề mặt khi mà r không đổi. Giá trị điện thế tỉ lệ nghịch với bán kính (với gốc tại nguồn đơn cực) và khi r tiến tới ∞ thì điện thế bằng 0.

Không phải luôn luôn thuận tiện nếu đặt gốc tọa độ tại nguồn điểm (ví dụ như xét nhiều nguồn). Trong trường hợp này, việc cần làm là phân biệt sự kết hợp của các nguồn điểm, chúng ta làm điều này bằng cách sử dụng các điểm trường. Khi đó trong công thức 8.7, r được cho bởi:

(8.8)

Trong đó mỗi nguồn đơn cực được đinh vị tại (x,y,z) trong khi điểm trường tại (x’,y’,z’).

Trường được mô tả bởi công thức 8.7 cho một điểm nguồn dòng là đồng nhất với trường tĩnh điện của một điện tích, thay thế I_o bởi Q_o (đại lượng điện tích), σ thay thế bởi ε (hằng số điện môi) và thay thế bởi . Kết quả này không có gì đáng ngạc nhiên bởi vì nếu những sự chuyển đổi trên được thực hiện thì những công thức áp dụng cho dòng điện chuyển đổi ăn khớp với những công thức trong tĩnh điện. Những giải thích cho các vấn đề trong tĩnh điện có thể được chuyển đổi để giải thích cho các vấn đề tương đương cho dòng điện.

Những điều đã nêu ở trên là một ví dụ của tính đối ngẫu. Nó có thể là một công cụ hữu hiệu khi đã có một tài liệu tổng quát tồn tại. Đôi khi nó có thể có những hạn chế. Ví dụ, một chất có độ dẫn suất bằng 0 nhưng hằng số điện môi có thể không bao giờ nhỏ hơn hằng số điện môi của chân không. Ngoài ra, một hệ có thể thể có một điện tích điểm, còn có hệ thậm chí không có một nguồn điểm vật lý.

Người đọc có thể ngạc nhiên vì sao lại có một sự quan tâm đối với một điểm nguồn dòng khi mà nó không có ý nghĩa thực tế. Một lý do đó là trong một khu vực có giới hạn, các trường có thể hoạt động như khi chúng bắt nguồn từ một nguồn (nguồn này được gọi là nguồn tương đương, tức là không có thật). Thứ hai, một hệ thực tế có 2 điểm nguồn của 2 cực đối nhau, trong trường hợp này, trường được quan tâm có thể được tìm thấy bằng cách xếp chồng các điểm nguồn trường. Trường hợp này sẽ được xem xét trong phần sau.

Lưỡng cực

Điều kiện đầu:

Nguồn: Lưỡng cực trong miền cố định

Bộ dẫn: Vô hạn, đồng chất

Trong điện sinh học có thể không bao giờ tồn tại nguồn dòng đơn cực vì sự bảo toàn điện tích. Nhưng việc kết hợp nguồn đơn cực âm và dương là có thể thực hiện được nếu như tổng của chúng có giá trị bằng 0. Cách kết hợp đơn giản nhất và phản ánh bản chất của điện sinh học, đó là nguồn lưỡng cực. Nguồn lưỡng cực gồm 2 đơn cực trái dấu nhưng bằng nhau về trị số I_o được tách biệt bới một khoảng cách rất nhỏ d. Thật ra, định nghĩa chặt chẽ đòi hỏi d→0,I_o→0 và p=I_od là hữu hạn.Đại lượng p là moment lưỡng cực hay đại lượng lưỡng cực.Lưỡng cực là một vector có hướng từ nguồn điểm âm đến nguồn điểm dương. Thật ra, nếu là chuyển vị từ điểm nguồn âm sang điểm nguồn dương và là một vector đơn vị theo phương đó, ta có:

(8.9)

trong đó = vector lưỡng cực.

Một lưỡng cực có hướng bất kì được minh họa trong hình 8.1, ở đó điểm gốc hệ trục tọa độ được đặt tại đơn cực âm. Nếu đơn cực dương cũng ở điểm gốc thì trường sẽ bằng 0. Bởi vậy, trường xuất hiện từ sự chuyển dời của đơn cực dương từ điểm gốc tới vị trí thực của nó (như trong hình 8.1), đó là trường lưỡng cực. Nhưng điều này có thể được tìm ra bằng cách kiểm tra biểu thức điện thế của đơn cực dương và đánh giá sự thay đổi điện thế gây ra bởi sự dịch chuyển đơn cực từ điểm gốc tới vị trí lưỡng cực của nó. Và điều này có thể được tính xấp xỉ bằng cách lấy đạo hàm bậc nhất của trường điện thế đơn cực theo hệ tọa độ nguồn được xem xét tại điểm gốc (như trong khai triển chuỗi Taylor). Cụ thể, để tìm được trường lưỡng cực, lấy tích phân của Φ (như cho bởi công thức 8.7) theo hướng ( tích phân có hướng) và sau đó nhân với độ lớn của d. Như vậy thể hiện trường lưỡng cực Φ_d và căn cứ vào công thức 8.7,ta có:

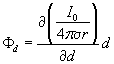(8.10)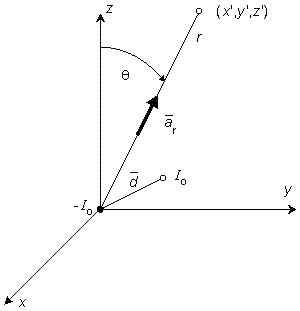

Hình 8.1. Lưỡng cực của –I_o tại gốc và nguồn I_o tại vector bán kính , trong đó d→0. Ngoài ra còn minh họa một điểm trường tại vector bán kính và góc lệch θ.

Đạo hàm có hướng trong công thức 8.10 bằng với thành phần của gradient theo phương :

(8.11)

Và cuối cùng, từ I_od=p, ta có:

(8.12)

Độ chính xác của công thức 8.10 được nâng cao khi d→0, và thực tế, p thường được xác định trong giới hạn là d→0, I→∞, và p=I_od. Do đó, công thức 8.12 là một biểu thức chặt chẽ cho một lưỡng cực được xác định bằng toán học.

Nếu các trục tọa độ được định hướng sao cho lưỡng cực hướng dọc theo trục z và lưỡng cực được đặt tại gốc, sau đó mang phép toán gradient trong công thức 8.12 ra ngoài:

(8.13)

Trong đó là hướng từ điểm nguồn tới điểm trường, chúng ta thu được trường cho 1 lưỡng cực:

(8.14)

và:

(8.15)

Trong công thức 8.15, góc lệch θ là góc lệch có định hướng. Các phương trình sau có thể được xác thực bằng cách chú ý rằng phép toán gradient (trong công thức 8.13) thực hiên trên hệ tọa độ nguồn trong công thức 8.8.

Một sự so sánh của trường lưỡng cực với trường đơn cực, bằng sự đối chiếu công thức 8.15 với công thức 8.7, thấy rằng trường lưỡng cực thay đổi theo (1/r²) trong khi trường đơn cực biến đổi theo (1/r). Ngoài ra, các mặt đẳng thế của trường lưỡng cực không phải là những mặt cầu đồng tâm, đúng hơn là nó phức tạp hơn bới có nhân tử cosθ. Điện thế lưỡng cực tối đa cho một giá trị của r nằm trên trục có cực (trục z).

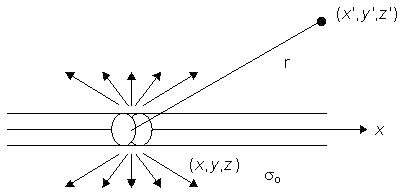
Mô hình sợi đơn độc lập: Nguồn dòng màng (Transmembrane Current Source)

Điều kiện đầu:

Nguồn: Sợi hoạt động có chiều dài hữu hạn hoặc vô hạn với tiết diện tròn.

Bộ dẫn: Vô hạn, đồng nhất.

Hình 8.2 minh họa một sợi dây hoạt động dài, mảnh nằm trong môi trường dẫn điện đồng chất với độ dẫn σ_o và kích thước không giới hạn. Nếu chúng ta giả sử có một xung thần kinh lan truyền, thì những dòng điện hoạt động được kết hợp với một phân bố dòng màng i_m(x). Do sợi rất mỏng và có trục đối xứng, chúng ta có thể mô tả dòng màng như một hàm của biến x. Như vậy nguồn mô tả là nguồn một chiều. Đơn vị của i_m(x) là dòng cho mỗi đơn vị chiều dài. Một phần nhỏ của dòng i_m(x)dx có thể được xem như một nguồn dòng điểm (nguồn đơn cực) trong môi trường ngoại bào. Vì vậy, từ công thức 8.7, ta có:

(8.16)

Trong đó r được cho bởi công thức 8.8, Φ_o là trường điện thế và σ_o là độ dẫn phía bên ngoài sợi (độ dẫn ngoại bào). Lấy tích phân toàn bộ sợi dây (theo x) cho ta trường tổng như sau:

(8.17)

Ở đây nguồn được giả sử nằm trên trục của sợi, tại tọa độ (x,0,0) và điểm trường có tọa độ (x’,y’,z’).

Chúng ta có thể sử dụng công thức suy ra trong chương 3, phần 3.4.2 cho sợi trong hình 8.2. Chúng ta có thể coi gần đúng rằng điện trở của môi trường giữa các điểm r_o≈0 và tương tự như vậy điện thế trong môi trường giữa các điểm Φ_o≈0. Sử dụng những sự xấp xỉ trên, công thức 3.42 và chú ý rằng Φ_i-Φ_o≈Vm, ta được:

(8.18) Hình 8.2. Một sợi mảnh dài được đặt vào môi trường dẫn điện đồng chất có độ dẫn σ_o và kích thước không giới hạn. Mật độ dòng màng được biểu diễn bằng i_m(x) sao cho i_m(x) được coi như một điểm nguồn trong môi trường ngoại bào.

Công thức 8.17 có thể được viết như sau:

(8.19)

Trong công thức 8.19, r được cho bởi:

(8.20)

Sử dụng biểu thức điện trở của hình trụ với ri=1/(πa²σ_i) căn cứ trên một độ dẫn σ_i bên trong tế bào, chuyển đổi công thức 8.19 thành:

(8.21)

Trong đó a = bán kính sợi.

Người đọc sẽ chú ý rằng ban đầu Φ_o được đưa về 0 và bây giờ lại tìm thấy một kết quả cho Φ_o, và tất nhiên, nó khác 0. Sự giải thích của nghịch lý này là do Φ_o được bỏ qua khi dẫn dắt công thức 8.18 trong sự so sánh với Φ_i. Do nhỏ hơn khoảng 100 lần nên Φ_o có thể được bỏ qua. Người đọc quan tâm có thể theo dõi vấn đề này bằng cách thay thế giá trị Φ_o tìm được trong công thức 8.21 vào trong dạng đầy đủ của công thức 8.18, đó là:

(8.18b)

Và sau đó tính toán lại Φ_o. Việc làm này sẽ cho ra một Φ_o chính xác hơn. Thực tế, phương pháp này có thể được lặp đi lặp lại đến khi đạt được kết quả mong muốn. Một phương pháp của Henriquez và Plonsey (1988) có thể tìm kết quả rất nhanh, chứng minh được rằng phép tính gần đúng (cho bởi công thức 8.21) là hoàn toàn thỏa đáng.

Công thức 8.21 có thể được kết hợp bởi nhiều phần. Ở vị trí giới hạn của không gian hoạt động, các điều kiện nghỉ tồn tại, =0 và các lớp kết hợp được nhặt ra ngoài. Vì vậy:

(8.22)

Hoặc:

(8.23)

Ở đây là vector đơn vị trong trục x.

Vì hai công thức 8.23 và 8.21 có cùng dạng toán học nên chúng nhất thiết phải đánh giá giống nhau về trường Φ_o. Trong công thức 8.21 thể hiện nguồn là mật độ dòng nằm trên trục, trong khi đó trong công thức 8.23 thể hiện nguồn là một lưỡng cực cũng nằm dọc trục. Tất nhiên, đó là 2 nguồn tương đương. Nguồn nào được thích sử dụng hơn phụ thuộc vào dạng của V_m(x), điều này sẽ được nói rõ hơn trong các phần sau.

Nhận xét về nguồn dòng màng

Công thức 8.17 mô tả một trường trong khối ngoại bào hình thành từ các thành phần dòng màng. Nó giới hạn cho sự đánh giá về điện thế bên ngoài tế bào và không phù hợp cho sự mô tả các trường bên trong nội bào.

Có 2 phép tính gần đúng làm cơ sở cho công thức 8.17 và cần phải nhớ. Đầu tiên, mỗi thành phần dòng được xem gần đúng như một nguồn điểm, nhưng dòng thực tế xuất hiện từ bề mặt màng không chỉ là một điểm (xem hình 8.2), và một bộ phận trục có thể được coi như một “nguồn vòng”. Đối với các sợi mảnh thì sự đơn giản hóa này có thể chấp nhận được. Thứ hai, biểu thức trường trong công thức 8.17 là chính xác cho một trường trong một không gian vô hạn, trong khi trên thực tế không gian lại bị giới hạn bởi chính sợi đó. Phép tính gần đúng này là hoàn toàn thỏa đáng. Tuy nhiên, môi trường ngoại bào tự bản thân nó giới hạn, vì vậy có lẽ không thể bỏ qua sợi dây và vấn đề giá trị giới hạn thực tế phải được giải quyết (Rosenfalck,1969).

Không gian ngoại bào vô hạn là quan trọng để đảm bảo không chỉ sử dụng trường nguồn điểm “không gian tự do” trong công thức 8.7 nhưng ngoài ra biểu thức dòng dẫn trong công thức 8.18 là cơ sở cho việc giả thiết rằng r0≈0 và Φ_i-Φ_o≈Vm. Đối với sợi dây đơn bán kính nhỏ, công thức 8.21 và 8.23 được đưa ra để hoàn chỉnh hơn (Trayanova,Henriquez và Plonsey,1990).

Mật độ nguồn khối tương đương

Điều kiện đầu:

Nguồn: Sợi hoạt động hữu hạn hoặc vô hạn với tiết diện tròn

Bộ dẫn: vô hạn, thuần nhất

Mật độ nguồn đơn cực tương đương

Sự giải thích vật lý cho công thức 8.21 có thể được đưa ra dựa trên sự mô tả trường của một nguồn đơn cực cho bởi công thức 8.7. Chúng ta chú ý rằng thể hiện như một nguồn dòng điểm.

Do vậy, là giá trị của dòng trên mỗi đơn vị chiều dài. Nói chung, đây là một hàm của x, sự biến thiên theo x tạo nên một sự mô tả của mật độ nguồn. Vì vậy, nguồn được tạo thành như nằm trên trục, nó có thể giải thích như một mật độ nguồn dải (line source density). Đây là một khái niệm định lượng cho các điểm nguồn của trường dẫn khối (xuất phát từ điện thế hoạt động mô tả bằng V_m(x)).

Có thể tập hợp các số hạng trong công thức 8.21 như sau:

(8.24)

Và bây giờ là giá trị của một mật độ nguồn khối (mật độ nguồn dòng) bởi vì πa2dx là một phần tử khối. Thực tế, sự giải thích của công thức 8.24 là nguồn được điền đầy vào khối bên trong sợi dây, ở đó mỗi phần tử nguồn là một vành tròn (disk) của khối: πa2dx. Mật độ nguồn là đồng nhất qua bất kì tiết diện ngang nào của vành tròn (disk). Tất nhiên, nguồn như trên là không có thật. Các nguồn này được xác định như là các nguồn tương đương. Tức là, chúng tương đương với các nguồn thực, việc tính toán cho các nguồn thực trong môi trường bên ngoài (sợi) từ những nguồn tương đương là chính xác. Để tính toán cho các nguồn thực trong môi trường bên trong (sợi) (hoặc một số các nguồn tương đương khác), chúng ta sẽ đi đến các phần tiếp theo của chương này.

Mật độ nguồn lưỡng cực tương đương

So sánh công thức 8.23 với công thức 8.12 phát hiện ra nguồn tương đương (của nguồn được mô tả bằng công thức 8.23) như một dải mật độ nguồn lưỡng cực. Sự kết hợp này được nêu bật bằng cách viết lại công thức 8.23 như sau:

(8.25)

Bây giờ có thể định nghĩa một phần tử lưỡng cực bằng . Lưỡng cực được định hướng theo chiều (+) trục x và mật độ dải lưỡng cực là .

Tùy theo lựa chọn, nguồn lưỡng cực có thể được kết hợp như , như một mật độ khối lưỡng cực (volume dipole density), nó điền đầy không gian bên trong sợi, được định hướng theo trục x và đồng nhất trên mọi tiết diện ngang. Do đó, một phần tử lưỡng cực cũng có thể được xem như một vành tròn (disk) của khối (πa2dx) với dạng vector là .

Nguồn tương đương tổng hợp: Mô hình ba cực (Tripole model)

Bây giờ xét điện thế hoạt động V_m(x) (điện thế màng trong khi hoạt động), lấy đạo hàm bậc 2 với x. Như ta đã biết, mật độ nguồn khối tương đương tỉ lệ với , được minh họa trong hình 8.3. Chú ý rằng các nguồn dương nằm trong khoảng x1<x<x2 và x3<x<x4 trong đó >0 , trong khi đó các nguồn âm nằm trong khoảng x2<x<x3, trong đó <0. Tổng các nguồn dương bằng tổng các nguồn âm. Trường bên ngoài tế bào được phát sinh bởi nguồn này, được quan sát theo 3 pha (2 miền của 1 phân cực được tách biệt bởi 1 miền của phân cực còn lại).

Khi khoảng cách tới điểm trường lớn hơn so với khoảng cách hướng trục của mỗi vùng nguồn âm hoặc dương, khi đó mỗi nguồn kể trên có thể được coi như một nguồn đơn cực tại trọng tâm (“center of gravity”) của sự phân bố nguồn tương ứng. Điều này được minh họa trong hình 8.3. Mô hình tổng hợp được mở rộng như một mô hình nguồn 3 cực (bao gồm 3 đơn cực). Bằng trực giác, chúng ta hi vọng điều đó hợp lý, khoảng cách từ mỗi phân bố nguồn tới điểm trường r_i thỏa mãn:

(8.26)

Ở đây r₁, r₂,r₃ giống như x₁, x₂, x₃ được minh họa trong hình 8.3. Dựa trên công thức 8.24, chúng ta có thể biểu diễn trường 3 cực như sau:

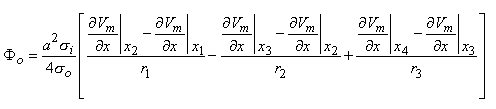(8.27)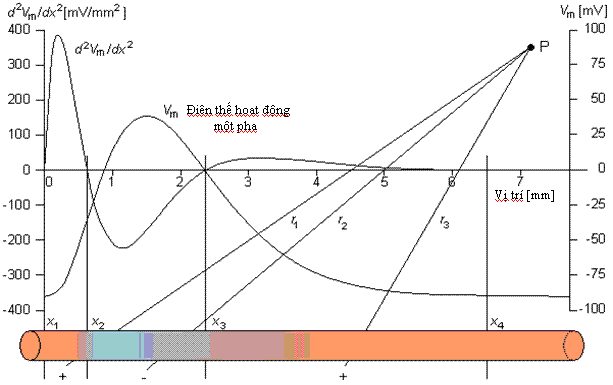

Hình 8.3. Điện thế hoạt động 1 pha V_m(x) và đạo hàm bậc 2 của nó . Như đã nói ở trên, mật độ nguồn khối tỉ lệ với . Vì vậy, các nguồn dương nằm trong khoảng x₁<x<x₂ và x₃<x<x₄ trong khi các nguồn âm nằm trong khoảng x₂<x<x₃. Các nguồn bên trong sợi được minh học ở phía dưới.Khi khoảng cách của mỗi phân bố nguồn nhỏ hơn so với khoảng cách tới trường, mỗi sự phân bố có thể được kết hợp thành nguồn tổng hợp. r₁,r₂, r₃ là các khoảng cách từ mỗi nguồn tổng đến điểm trường P.

Cơ sở toán học cho nguồn lớp kép (bó sợi đồng chất)

Điều kiện đầu :

Nguồn: Bó sợi hoạt động chiều dài hữu hạn hoặc vô hạn với tiết diện tròn

Bộ dẫn: Vô hạn, thuần nhất

Biểu thức cho mật độ khối nguồn lưỡng cực trong phần 8.3.2 được cho bởi nhưng điều này được suy ra cho một sợi độc lập. Đối với bó sợi, có thể được đưa ra là (Plonsey và barr, 1987), trong đó C là một hệ số phụ thuộc vào độ dẫn bên trong và bên ngoài tế bào và hình dáng của bó sợi. Giá trị của nó bình thường vào khoảng 0.4.

Hình 8.4 minh họa sự lan truyền của giai đoạn tăng lên của một điện thế hoạt động dọc một bó sợi đồng chất. Trong hình này, vùng bờ giới hạn đầu tiên và tiếp theo của vùng hoạt động (nơi mà ≠0) được giả sử là phẳng. Tất cả các sợi dây trong bó được giả sử là song song và mang những điện thế hoạt động như nhau. Vì vậy, mỗi sợi dây sẽ bao gồm một mật độ nguồn tương đương như nhau. Điều này được xem như một mật độ nguồn lưỡng cực và vì vậy tỉ lệ với - . Chú ý rằng trong vùng đã kể trên, hàm - là một pha, và vì vậy các nguồn lưỡng cực được định hướng hết theo một hướng như nhau.

Khi khoảng cách của quá trình tăng lên của điện thế hoạt động x₂-x₁ trong hình 8.4) nhỏ so với khoảng cách tới điểm trường P, khi đó sự phân bố lưỡng cực theo trục trong một tiết diện ngang có thể được thay thế bởi một lưỡng cực tổng. Trong trường hợp này, nguồn phát sinh trong bó sợi như một khối toàn bộ có thể được xem xấp xỉ như một bản lưỡng cực, hay lớp kép (double layer). Đối với cơ tim, bởi vì các tế bào liên kết chặt chẽ, bó sợi trong hình 8.4 là một phép tính xấp xỉ tốt cho việc thể hiện sự lan truyền sóng trong tất cả các vùng cơ tim không phụ thuộc sự định hướng các sợi.

Các phép đo trên động vật thí nghiệm cho phép xác định một cách liên tục theo thời gian và theo bề mặt tạo ra sự tăng lên xa nhất của sự lan truyền. Theo những điều đã nêu trên, những “bề mặt đẳng thời” (isochronal surfaces) có thể cũng được nhìn thấy, tại mỗi thời điểm, như vị trí của nguồn lớp kép. Do bề dày của giai đoạn tăng lên của sự lan truyền xung hoạt động tim chỉ khoảng 0.5 mm, điều kiện để mà nó là nhỏ so với khoảng cách tới điểm trường gần như luôn luôn được thỏa mãn khi phép đo điện tim được thực hiện trên bề mặt cơ thể. Mô hình nguồn lớp kép được nghiên cứu rất nhiều để làm cơ sở cho phép đo điện tim.

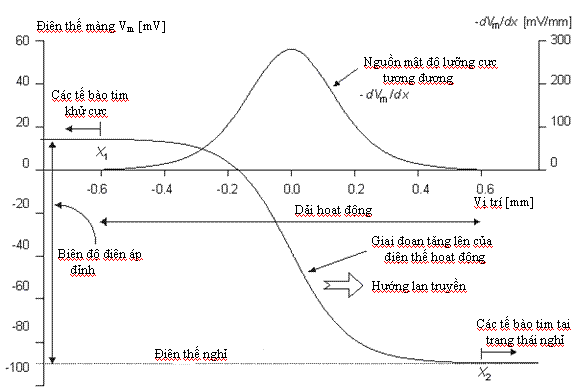
Hình 8.4. Giai đoạn tăng lên của sự lan truyền lý tưởng điện thế hoạt động qua màng đối với một tế bào cơ tim được kí hiệu V_m. Sóng được lan truyền theo hướng từ trái qua phải. Nguồn mật độ lưỡng cực tương đương tỉ lệ với - , như được minh họa. Một sự biểu diễn vật lý của sự phân bố lưỡng cực cũng được nhìn chỉ rõ. Các lưỡng cực nằm trong khoảng x₁<x<x₂.

Công thức hoàn chỉnh

Trường của một tế bào đơn có hình dạng bất kì

Điều kiện đầu:

Nguồn: Tế bào đơn có hình dạng bất kì

Bộ dẫn: vô hạn, thuần nhất

Mối quan hệ nguồn - trường đối với một sợi độc lập được mô tả bằng công thức 8.17, là công thức xác định mật độ nguồn như một dòng xuyên màng. Nó hướng ra ngoài để khi đạt được biểu thức này, nguồn được tính xấp xỉ như một điểm (đúng hơn là một vòng), và do đó ảnh hưởng của chính sợi dây trong phạm vi độ dẫn khối được bỏ qua. Đối với sợi độc lập, ở đó kích thước của xung thần kinh là lớn hơn so với bán kính của sợi, nó có thể được chỉ ra để phương trình dòng - nguồn của công thức 8.17 thỏa mãn (Trayanova,Henrique và Plonsey, 1989).

Khi các điều kiện này chưa được thỏa mãn, nó được mô tả để có một biểu thức nguồn chặt chẽ. Có thể chỉ ra được rằng đối với một tế bào hoạt động hình dạng bất kì với bề mặt S, trường phát sinh từ một điểm P, bên ngoài hay bên trong tế bào, đó là:

(8.28)

Trong đó : Ф_p=trường tại điểm P

Ф_i=điện thế ngay bên trong màng

Ф_o=điện thế ngay bên ngoài màng

σ_i=độ dẫn bên trong màng

σ_i=độ dẫn bên ngoài tế bào

σ_p=độ dẫn tại điểm trường

Nguồn được định nghĩa bởi công thức 8.28 là một lớp kép nằm trên bề mặt tế bào, cường độ của nó là và hướng của nó dọc theo bề mặt bên ngoài (Plonsey,1974). Điểm trường P trong công thức 8.28 có thể áp dụng cho môi trường bên trong và bên ngoài tế bào.

Trường của một sợi trụ độc lập

Điều kiện đầu:

Nguồn: Sợi trụ độc lập

Bộ dẫn: Vô hạn, thuần nhất

Nếu áp dụng công thức 8.28 cho một sợi trụ độc lập thì giả thiết Ф_o≈0 (khi đó Ф_i- Ф_o≈Vm), cho ra:

(8.29)

Trong đó phép lấy tích phân tiến hành trên tiết diện ngang có diện tích A. Nếu điểm trường nằm tại khoảng cách xa so với bán kính thì công thức 8.29 được rút gọn thành công thức 8.21 và công thức 8.17, vì vậy công việc sẽ dễ dàng hơn khi các phép tính xấp xỉ này được thỏa mãn.

Cơ sở toán học cho mật độ nguồn khối vĩ mô (mật độ nguồn dòng) và mật độ dòng tác động

Điều kiện đầu:

Nguồn: Lớp của các phần tử nguồn lưỡng cực

Bộ dẫn: Vô hạn, thuần nhất

Trong phần này chúng ta thảo luận vê cơ sở toán học của các định nghĩa của mật độ nguồn khối (mật độ nguồn dòng), I_F và mật độ dòng tác động, .

Vì là một hệ quả của quá trình kích thích trong mô tim, tim thể hiện như một nguồn của các dòng và sinh ra các điện thế trong độ dẫn khối xung quanh. Các nguồn này bao gồm các lớp của các phần tử nguồn lưỡng cực, nằm trong các bề mặt hoạt động đẳng thời, như đã trình bày ở trước. Sự mô tả này chỉ là một phép xấp xỉ, vì nó dựa trên giả thiết rằng mô tim là đồng nhất và đẳng hướng.

Theo nguyên lý, công thức 8.28 có thể được áp dụng cho mỗi tế bào trong tim. Vì một tế bào tim là rất nhỏ so với kích thước có thể quan sát được, vector bán kính trong công thức 8.28 có thể được giả sử là hằng số trong phép tính tích phân trên mỗi tế bào. Vì vậy mỗi tế bào có thể có thể được xem như một nguồn lưỡng cực tổng hợp đơn, hay đơn giản là tổng vector của nó là các phần tử bề mặt lớp kép. Đó là lưỡng cực cho tế bào thứ j, được cho bởi:

(8.30)

Vì tim có khoảng 5.10¹⁰ tế bào, có lẽ 5% trong số đó được kích thích tại mọi thời điểm trong suốt quá trình khử cực nên độ số lượng của các phần tử nguồn lưỡng cực là rất lớn. Dưới các điều kiện này có thể định nghĩa một hàm mật độ moment khối lưỡng cực (tức là, một lưỡng cực cho một đơn vị khối) bằng cách lấy trung bình các phần tử lưỡng cực trong mỗi khối nhỏ. Đó là:

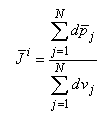(8.31)

trong đó mẫu số là tổng khối đang sử dụng bằng một nhóm N tế bào, và dS_j là bề mặt của mỗi phần tử khối dv_j. N đủ nhỏ để có thể đạt được một “độ phân giải”(resolution) tốt, nhưng đủ lớn để hàm liên tục từ điểm tới điểm. Công thức 8.31 đôi khi được mô tả như trung bình các “hạt thô” (coarse-grained average), vì chúng ta không để cho khối mà ta lấy trị trung bình trên đó tiến tới 0. Các sự xem xét tương tự được áp dụng, ví dụ, trong tĩnh điện, trong đó mật độ điện tích được xem xét một cách thông thường để là một hàm trơn.

Hàm nguồn là một hàm mật độ lưỡng cực (khối). Vì vậy, trường nó sinh ra có thể được tìm thấy bằng phương pháp chồng chất, ở đây dv là một lưỡng cực đơn được áp dụng trong công thức 8.12. Do đó, trường tổng từ tất cả các thành phần trên là:

(8.32)

Nếu áp dụng phép đồng nhất vector cho công thức 8.32 thì có:

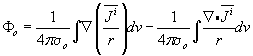(8.33)

Định luật Gauss có thể được áp dụng cho vế phải của công thức 8.33, và từ =0 tại S (tất cả các phần tử nguồn nằm bên trong tim, ko có phần tử nào nằm trên bề mặt của phép lấy tích phân), ta được:

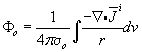
Đối chiếu với công thức 8.7 cho ta:

(8.35)

là một mật độ nguồn khối (nguồn dòng).

Như đã trình bày trong phần 7.2.2, có thể giải thích như một mật độ dòng tác động. Mật độ dòng này được tồn tại bằng cách sử dụng năng lượng hóa học (tức là sự di chuyển của các ion là nhờ có bậc thang nồng độ). Đó là nguyên nhân chính cho sự hình thành của một điện trường. Ngược lại, chúng ta chú ý rằng mật độ dòng, = σ , đã được mô tả bằng định luật Ohm trong Công thức 8.4, đã bị suy giảm. Các dòng tác động không phải được tạo ra bởi điện trường , bởi vậy nó được tạo ra bởi một nguồn năng lượng không có bản chất điện.

Tổng kết về các mô hình nguồn trường

---

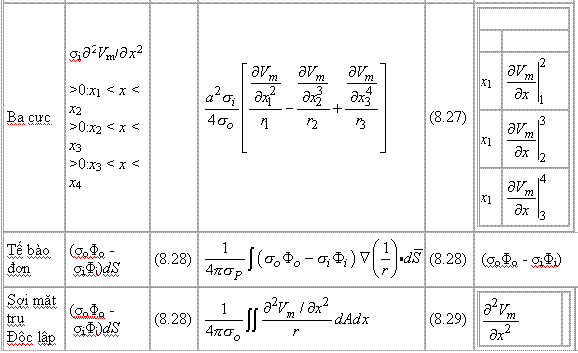
trang trước

Mô hình nguồn trường

Trang tiếp

Liên kết đến đây

• Sách:Điện từ sinh học
• Sách:Điện từ sinh học/Mô hình lưỡng miền của các bộ dẫn khối đa tế bào
• Sách:Điện từ sinh học/Nguồn khối và bộ dẫn khối