Sách:Điện từ sinh học/Nguồn khối và bộ dẫn khối

Khái niệm về nguồn khối và bộ dẫn khối

Lĩnh vực khoa học có liên quan nhiều nhất tới điện sinh lí học ( electrophysiology ) và điện từ sinh học ( bioelectromagnetism ) chính là kĩ thuật điện. Tuy nhiên, sinh viên ngành điện sẽ nhanh chóng nhận ra những điểm khác biệt chính giữa các lĩnh vực này. Rất nhiều kĩ thuật của ngành điện liên quan tới các nguồn pin, điện trở, tụ điện và cuộn cảm. Mỗi thứ trong số các thành phần này được coi là rời rạc. Các mạch điện và các mạng điện đã được nghiên cứu sâu hơn để làm sáng tỏ các tính chất về cấu trúc của chúng.

Trong điện sinh lí học và điện từ sinh học thì không có thành phần điện cảm, trong khi các điện trở, tụ điện, nguồn pin lại không phải rời rạc và được phân bố theo quy luật. Đó là môi trường dẫn được mở rộng 1 cách liên tục. Nó là mảng các không gian 3 chiều và được coi là 1 bộ dẫn khối .

Nguồn điện sinh học và điện trường của nó

Xác định điều kiện đầu

Các phần mà chúng ta sẽ thảo luận ở dưới đây chỉ chính xác khi được đặt dưới một tập điều kiện - đó là, nó chỉ đúng đối với các dạng nguồn điện nằm dưới dạng các bộ dẫn khối. Vì vậy, một vài giả thiết giới hạn hay các điều kiện đầu được đưa ra trước tiên.

Chúng ta cần chú ý rằng: khi các điều kiện đầu chặt chẽ hơn các điều kiện thực tế thì các nghiên cứu sẽ càng có hiệu quả hơn. Chẳng hạn như: nếu các điều kiện đầu chỉ ra rằng các nghiên cứu chỉ chính xác với một bộ dẫn khối thuần nhất vô hạn thì nó sẽ không đúng với một bộ dẫn khối không thuần nhất hữu hạn. Mặt khác, nếu các điều kiện đầu chỉ ra rằng: các nghiên cứu là đúng với một bộ dẫn khối không thuần nhất hữu hạn thì nó cũng đúng với một bộ dẫn khối thuần nhất vô hạn vì cái sau chỉ là trường hợp đặc biệt của cái trước.

Chúng ta nên chú ý rằng: tất cả các bộ dẫn khối được giả thiết là tuyến tính ( linear ). Nếu bộ dẫn khối được coi như đồng nhất, nó cũng được giả định là đẳng hướng. Những dạng nguồn và bộ dẫn khác nhau sẽ được mô tả ở phần sau của chương này.

Nguồn khối trong bộ dẫn khối thuần nhất

Điều kiện đầu:

Nguồn: nguồn khối

Bộ dẫn: vô hạn, thuần nhất

Chúng ta hãy cùng đưa ra khái niệm về mật độ dòng tác động 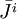${\bar {J^{{i}}}}$ (x,y,z,t). Đây là dòng không bảo toàn mà nó tăng lên từ hoạt động điện sinh học của tế bào thần kinh và tế bào cơ, do sự chuyển đổi năng lượng từ dạng hóa năng sang điện năng. Các thành phần riêng rẽ của các nguồn điện sinh học này được coi như các lưỡng cực dòng điện ( electric current dipoles ). Do đó, mật độ dòng điện tác động bằng mật độ momen lưỡng cực khối của nguồn. Chú ý rằng 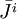${\bar {J^{{i}}}}$ bằng không tại những vùng nằm bên ngoài tế bào hoạt động (active cell ).

Nếu bộ dẫn khối là vô hạn, thuần nhất và có độ dẫn là σ thì các nguồn chính 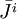${\bar {J^{{i}}}}$ tạo nên một điện trường E và một dòng điện dẫn có giá trị bằng σE. Kết quả là: mật độ dòng điện tổng được xác định bởi:

(7.1)

Giá trị σE thường được coi là giá trị dòng điện quay về ( return current ). Dòng này cần để tránh sự tích lũy điện tích do nguồn dòng tạo nên.

Bởi vì điện trường E là ghép tĩnh điện ( quasistatic ) ( xem phần 7.2.4) nên nó có thể được biểu diễn tại mỗi khoảng thời gian như là sự biến thiên của điện thế vô hướng Ф và công thức 7.1 có thể viết lại như sau:

(7.2)

Vì điện dung của mô là không đáng kể ( các điều kiện ghép tĩnh điện ) nên các điện tích nạp sẽ tự phân bố lại trong 1 khoảng thời gian ngắn để tương thích với bất kể sự thay đổi nào từ nguồn. Do sự khác nhau của giá trị J tính toán theo tốc độ thay đổi mật độ điện tích với thời gian và mật độ điện tích nạp phải bằng không nên các giá trị chênh lệch của J phải bằng không. Do đó, công thức 7.1 trở thành công thức Poisson:

(7.3)

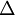
Công thức 7.3 là công thức vi phân từng phần biểu diễn theo Ф , trong đó 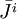$\Delta$ ${\bar {J^{{i}}}}$ là hàm nguồn ( source function hay forcing function )

Tính công thức 7.3 theo hàm vô hướng với một vùng đồng nhất và vô hạn, ta có:

(7.4)

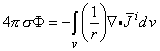
Trong đó :

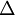
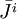$\Delta$ ${\bar {J^{{i}}}}$ dv trong công thức 7.4 được coi là nguồn điểm trong đó nó thiết lập nên 1 trường , biến đổi theo 1/r

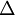
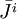$\Delta$ ${\bar {J^{{i}}}}$ được định nghĩa như mật độ nguồn dòng ( IF )

Do chúng ta tìm kiếm các giải pháp cho các điểm trường bên ngoài vùng xác định của nguồn khối nên công thức 7.4 có thể viết lại:

(7.5)

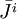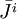Công thức trên biểu diễn sự phân bố của điện thế Ф theo nguồn điện sinh học ${\bar {J^{{i}}}}$ trong một bộ dẫn khối thuần nhất và vô hạn có độ dẫn σ. Ở đây, ${\bar {J^{{i}}}}$ dv được coi là thành phần lưỡng cực.

Nguồn khối trong bộ dẫn khối không thuần nhất

Điều kiện đầu:

Nguồn: nguồn khối

Bộ dẫn: không thuần nhất

Trong phần 7.2.2, chúng ta đã giả thiết rằng môi trường là đồng nhất. Giả thuyết như vậy cho phép ta sử dụng các công thức đơn giản, chỉ đúng với các môi trường đồng nhất và thuần nhất ( uniform homogeneous media ). Tuy nhiên, các môi trường thực tế nhìn chung là không thuần nhất. Trong phần này, chúng ta sẽ xem xét tính không thuần nhất bằng cách xấp xỉ bộ dẫn khối bởi các vùng mà mỗi vùng được coi như là thuần nhất, thuần trở và đẳng hướng trong đó mật độ dòng điện 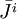${\bar {J^{{i}}}}$ quan hệ tuyến tính với điện trường E.

Một bộ dẫn khối không thuần nhất có thể được chia thành một số lượng hữu hạn các vùng thuần nhất với đường bao quanh là S_j. Trên các đường bao này, cả điện thế Ф và thành phần thông thường của mật độ dòng cần phải liên tục:

(7.6) (7.7)

Trong đó, thành phần có 1 dấu phẩy và 2 dấu phẩy trên đầu biểu thị cho các cạnh đối diện nhau của đường bao và n_j có hướng từ vùng 1 phẩy ( vùng đại diện bởi thành phần có 1 dấu phẩy trên đầu ) tới vùng 2 phẩy ( vùng đại diện bởi thành phần có 2 dấu phẩy trên đầu )

Nếu dv là 1 thành phần khối, ψ và Ф là 2 hàm số vô hướng (về mặt toán học, chúng được coi là hoạt động trong vùng thuần nhất ), ta có thể áp dụng quy luật Green:

(7.8)

Nếu chúng ta chọn ψ = 1/r với r là khoảng cách từ 1 điểm thuộc trường tới thành phần phần của khối hay của vùng tổ hợp và Ф là điện thế thì khi thay công thức 7.3 , 7.6 , 7.7 vào 7.8 , ta được kết quả:

(7.9)

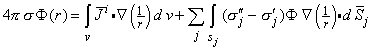
Đây là công thức tính điện thế tại 1 điểm bất kì trong bộ dẫn khối không thuần nhất chứa đựng các nguồn khối trong đó.

Thành phần đầu tiên bên vế phải của công thức 7.9 liên quan tới Jⁱ tương ứng với thành phần xuất hiện trong công thức 7.5 và do đó, biểu thị sự phân bố của nguồn khối. Tác động của tính không thuần nhất được phản ánh thông qua biểu thức tích phân thứ 2 , trong đó 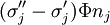$(\sigma ''_{{j}}-\sigma '_{{j}})\Phi n_{{j}}$ là một nguồn bậc 2 tương đương ( equivalent double layer source )

Chúng ta có thể viết lại công thức 7.9 như sau :

(7.10)

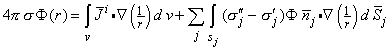
Mục đích của việc đo các tín hiệu điện sinh học là đo nguồn của chúng. Do đó, các hệ thống đo phục vụ cho điều trị bệnh nên thiết kế để sự phân bố của thành phần thứ 2 trong biểu thức 7.9 là nhỏ nhất có thể .

Điều kiện ghép tĩnh điện ( quasistatic condition )

Trong việc mô tả các nguồn khối được cấu thành bên trong cơ thể người, thành phần điện dung của trở kháng mô là không đáng kể trong dải tần của các tín hiệu điện sinh học bên trong cơ thể (theo kết quả nghiên cứu của Schwan và Kay (1957)). Các dòng điện dẫn khối (volume conductor currents) chủ yếu là dòng dẫn (conduction current) và chỉ phụ thuộc vào điện trở của mô. Những tác động của việc truyền sóng điện từ cũng có thể được bỏ qua (Geselowitz, 1963).

Điều kiện này chỉ ra rằng: các điện áp và dòng điện sinh học biến thiên theo thời gian trên cơ thể người có thể được nghiên cứu trong giới hạn ghép tĩnh điện thông thường ( conventional quasistatic limit ). Đó là: tất cả dòng điện và trường hoạt động ở bất kì thời điểm nào như thể chúng không thay đổi. Sự mô tả về các trường được tạo nên từ các nguồn dòng (current source) được dựa trên những hiểu biết về các môt trường có trở kháng và có thể bỏ qua sự biến thiên thời gian.

Khái niệm về mô hình hóa

Mục đích của mô hình hóa

Một phương pháp nghiên cứu chức năng của các cơ quan sống trên cơ thể là xây dựng các mô hình mô phỏng hoạt động của các cơ quan một cách chính xác đến mức có thể. Mô hình này có thể coi như tượng trưng cho các giả thuyết ứng với các quan sát vật lý. Thông thường thì các điểm trong giả thuyết thường làm phức tạp hóa mối tương tác giữa các biến mà mối quan hệ phụ thuộc lẫn nhau của chúng rất khó xác định bằng thực nghiệm. Hoạt động của các mô hình nên được điều khiển bởi các định luật cơ bản trong khoa học (ví dụ như định luật Ôm, định luật Kirchhop, các định luật nhiệt động học …).

Mục đích của mô hình là nhằm rút ra các kết luận và biểu hiện sống động các giả thuyết được đưa ra. Có thể thực hiện các thí nghiệm với mô hình trong khi không thể làm điều này với các cơ thể sống. Các mô hình đưa ra các thông tin đầu ra dựa trên các thông số cấu trúc và các đầu vào khác nhau. Chúng ta có thể hiểu rõ hơn các hiện tượng thực tế thông qua việc so sánh kết quả trên mô hình với kết quả thực tế. Bản thân mô hình cũng có thể được cải tiến theo cách này. Một giả thuyết không thể được chấp nhận trước khi nó được phân tích đầy đủ và chứng minh một cách chi tiết.

Một mô hình cần phải được xem xét đánh giá. Ví dụ, người ta khẳng định rằng các mô hình không thể biểu diễn hết được tất cả các hiện tượng sinh học. Tuy nhiên, chúng ta cũng nên lưu ý rằng tất cả các khái niệm của chúng ta đều dựa trên các mô hình.

Các mô hình cơ bản về nguồn khối

Bây giờ, chúng ta hãy cùng xem xét một số mô hình nguồn khối cơ bản và các hệ số không xác định hay các biến độc lập tương ứng của chúng.

Lưỡng cực

Mô hình lưỡng cực là dựa trên một lưỡng cực đơn với vị trí cố định, hướng và biên độ biến đổi. Mô hình này có 3 loại biến độc lập là biên độ của 3 thành phần của nó theo hệ trục Đề các là x, y, z.

Lưỡng cực chuyển động

Mô hình lưỡng cực chuyển động là một lưỡng cực đơn có biên độ và hướng thay đổi giống như lưỡng cực cố định nhưng có vị trí thay đổi. Do đó, nó có tới 6 biến độc lập.

Đa lưỡng cực

Mô hình đa lưỡng cực gồm một vài lưỡng cực, mỗi lưỡng cực biểu diễn một vùng giải phẫu của tim. Các lưỡng cực này cố định về phân bố vị trí và có biên độ thay đổi, hướng thay đổi. Nếu hướng của đa lưỡng cực cũng cố định thì mỗi lưỡng cực chỉ có duy nhất một biến độc lập, đó là biên độ. Khi đó, số biến độc lập sẽ bằng với số lưỡng cực.

Đa cực

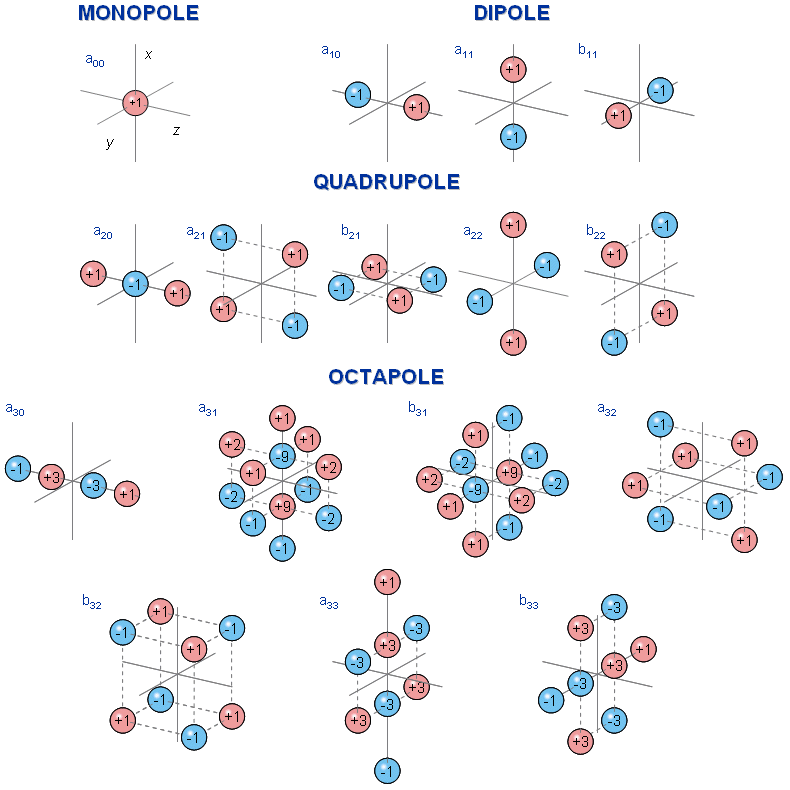
Lưỡng cực được tạo nên từ 2 cực đơn bằng nhau nhưng ngược dấu, được đặt cạnh nhau. Một mạng 4 cực được tạo nên từ 2 lưỡng cực bằng nhau nhưng ngược dấu, đặt cạnh nhau. Chúng ta có thể tạo được nguồn với số cực nhiều hơn bằng cách tiếp tục thực hiện như trên. Mỗi nguồn như vậy được coi là 1 đa cực. Điểm quan trọng về các đa cực là chúng có thể chỉ ra được các cấu hình của nguồn được đưa ra và nó có thể được biểu diễn bằng một tổng vô hạn các đa cực tăng theo bậc mũ. Kích thước của mỗi đa cực thành phần phụ thuộc vào phân bố nguồn đặc biệt. Mỗi thành phần của đa cực lại lần lượt được xác định bởi một số các hệ số. Ví dụ, ta thấy lưỡng cực được mô tả bởi 3 hệ số. Mạng 4 cực có 5 hệ số và cứ thế tiếp tục ... Đa cực có thể được minh họa theo nhiều cách khác nhau. Một trong số đó là đa cực điều hòa cầu ( spherical harmonic multipole ). Đa cực này được biểu diễn trong hình 7.1.

Tổng kết các mô hình nguồn và các biến độc lập được đưa ra trong bảng 7.1. Cấu trúc của các mô hình được biểu diễn trong hình 7.2.

Bảng 7.1. Các mô hình nguồn khác nhau và số lượng biến độc lập

Mô hình	Số biến độc lập
Lưỡng cực	3
Lưỡng cực chuyển động	6
Đa lưỡng cực	n,(3n)*
Đa cực
Lưỡng cực	3
Mạng Bốn cực	5
Mạng 8 cực	7

n đối với các lưỡng cực có hướng cố định

3n đối với các lưỡng cực có hướng thay đổi

Hình 7.1 . Mô tả các thành phần đa cực điều hòa cầu

Hình 7.2.Các mô hình sử dụng để biểu diễn nguồn khối 1)Lưỡng cực

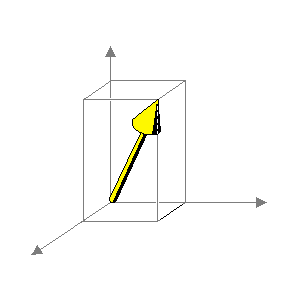
Phân bố cố định

Hướng tự do

Biên độ tự do

3 biến

2)Lưỡng cực chuyển động

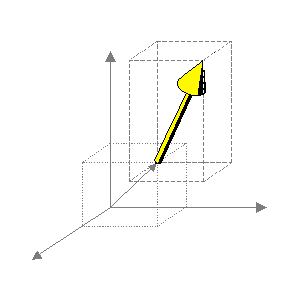
Phân bố tự do

Hướng tự do

Biên độ tự do

3 + 3 = 6 biến

3) Đa lưỡng cực

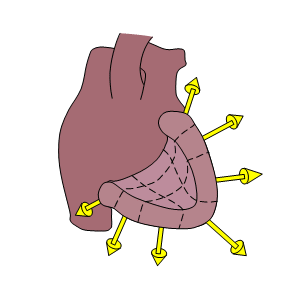
Số lưỡng cực = N

Phân bố cố định

Hướng tự do

Biên độ tự do

3N biến

Nếu hướng cố định: N thay đổi

4) Đa cực

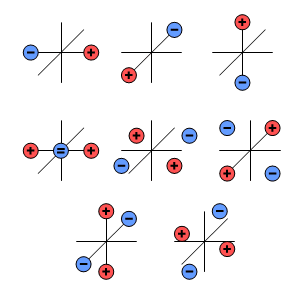
Mở rộng đa cực bậc cao

Số biến

lưỡng cực  : 3

mạng 4 cực  : 5

mạng 8 cực  : 7

Các mô hình cơ bản của bộ dẫn khối

Bộ dẫn khối có thể được mô hình hóa theo một trong số các cách sau đây và chúng ta phân chia chúng theo mức độ phức tạp khó dần.

Vô hạn, thuần nhất

Mô hình thuần nhất của bộ dẫn khối cùng với một sự mở rộng vô hạn thường ít quan trọng. Nó hoàn toàn bỏ qua các ảnh hưởng của đường bao bộ dẫn khối và tính không thuần nhất bên trong.

Hữu hạn, thuần nhất

Dạng hình cầu: dạng đơn giản nhất của các mô hình thuần nhất hữu hạn là mô hình dạng cầu (với nguồn là trung tâm của nó). Nó chỉ ra rằng: đối với nguồn lưỡng cực thì trường tại bề mặt có dạng giống với trường hợp bộ dẫn khối vô hạn thuần nhất tại cùng một bán kính ngoại trừ có biên độ của nó là lớn gấp 3 lần mà thôi. Do đó, có thể coi nó là một trường hợp không quan trọng.

Dạng thực tế, thuần nhất: bộ dẫn khối thuần nhất có giới hạn hoặc hữu hạn cùng với hình dạng thực tế có xem xét đến ảnh hưởng của đường bao ngoài bộ dẫn nhưng nó lại bỏ qua tính không thuần nhất ở bên trong.

Hữu hạn, không thuần nhất

Mô hình hữu hạn không thuần nhất đưa ra các kích thước hữu hạn của bộ dẫn và một hoặc nhiều hơn các tính chất không thuần nhất bên trong.

Phần thân người - Mô cơ tim - Lượng máu trong tim có độ dẫn cao - Mô phổi có độ dẫn thấp - Lớp cơ bề mặt - Các xương không dẫn điện như xương sống và xương ức - Các bộ phận khác như các mao mạch lớn,gan...

Đầu : Đối với đầu, các vùng dẫn đặc trưng được coi như 1 bộ dẫn khối là: - Não - Tuỷ sống thuộc não - Sọ - Các cơ - Da đầu không tính tóc

Các mô hình bộ dẫn khối được tổng kết trong bảng 7.2. Trở kháng của các mô khác nhau được chỉ ra trong bảng 7.3.

Các mô hình nguồn	Các tính chất
Vô hạn thuần nhất	Không quan trọng Không tính đến các tính chất điện của bộ dẫn khối hay các vùng biên của nó với không khí
Hữu hạn thuần nhất a.Dạng hình cầu b.Dạng thực tế	Không quan trọng nếu nguồn là 1 lưỡng cực Có tính đến cả hình dạng của đường bao ngoài phần ngực nhưng không quan tâm tới tính không thuần nhất bên trong
Hữu hạn không thuần nhất	Tính tới cả hình dạng bên ngoài của phần ngực và tính không thuần nhất bên trong

Bảng 7.2. Các mô hình bộ dẫn khác nhau và các tính chất của nó

Cơ thể người được coi như 1 bộ dẫn khối

Trở kháng mô ( Tissue Resistivities )

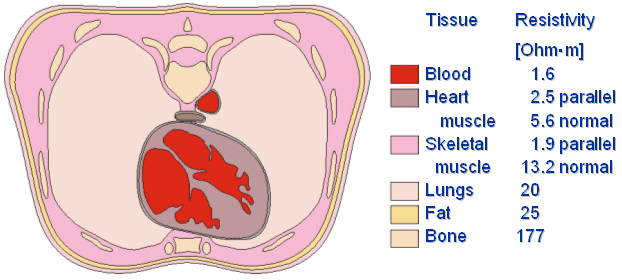
Cơ thể người có thể xem như một bộ dẫn khối tuyến tính, thuần nhất và có trở kháng. Đa số các mô là đẳng hướng. Tuy nhiên, cơ rõ ràng là không đẳng hướng và các mô não (brain tissue) cũng không đẳng hướng. Hình 7.3 mô tả lát cắt của vùng ngực và bảng 7.3 tổng kết lại trở kháng mô của một số cơ quan trên cơ thể người. Bảng liệt kê đầy đủ hơn về trở kháng mô được đưa ra trong Geddes và Baker (1967), Barber và Brown (1984), Stuchly và Stuchly (1984).

Mô	ρ[Ωm]	Ghi chú	Tham khảo
Não	2,2 6,8 5,8	Vật liệu xám Vật liệu trắng Trung bình	Rush and Driscoll, 1969 Barber and Brown, 1984 " " "
Chất dịch tủy của não	0,7		Barber và Brown, 1984
Máu	1,6	Hct = 45	Geddes và Sadler, 1973
Thể plasma	0,7		Barber và Brown, 1984
Cơ tim	2,5 5,6	Theo chiều dọc Theo chiều ngang	Rush, Abildskov, và McFee, 1963
Cơ xương	1,9 13,2	Theo chiều dọc Theo chiều ngang	Epstein vàFoster, 1982
Gan	7		Rush, Abildskov,và McFee, 1963
Phổi	11,2 21,7		Schwan vàKay, 1956 Rush, Abildskov, và McFee, 1963
Mỡ	25		Geddes và Baker, 1967
Xương	177 15 158 215	Theo chiều dọc Theo chiều ngang Theo phương bán kính (tại 100kHz)	Rush và Driscoll, 1969 Saha và Williams, 1992

Bảng 7.3. Giá trị trở kháng của các mô khác nhau

Hình 7.3. Lát cắt của ngực. Giá trị trở kháng được đưa ra cho 6 loại mô khác nhau

Trở kháng của máu rõ ràng phụ thuộc vào tỉ lệ thể tích huyết cầu (hematocrit) (phần trăm thể tích của tế bào máu trong toàn bộ máu) (Geddes và Sadler, 1973). Đây là sự phụ thuộc theo hàm mũ và nó được biểu diễn dưới công thức 7.11:

ρ = 0,537 e^0,025Hct (7.11)

Hugo Fricke đã nghiên cứu lí thuyết về độ dẫn điện của thể vẩn trong các khối hình cầu (Fricke, 1924). Khi áp dụng phương pháp này để đo độ dẫn của máu, chúng ta đạt được một đẳng thức gọi là công thức Maxwell-Fricke:

(7.12)

Trong đó ρ = trở kháng của máu [Ωm] Hct = tỉ lệ thể tích huyết cầu (hematocrit) [%]

Cả hai đẳng thức trên đều đưa ra giá trị chính xác. Hệ số tương quan giứa công thức 7.11 và phép đo thực nghiệm là 0,989. Vì đường cong vẽ trên biểu đồ ứng với các giá trị trở kháng đo được là không tuyến tính nên công thức 7.12 đưa ra các giá trị tốt hơn với hct rất thấp hoặc rất cao. Trở kháng của máu cũng phụ thuộc vào sự di chuyển của máu (Liebman, Pearl, và Bagnol, 1962; Tanaka et al., 1970). Ảnh hưởng này thường xuyên bị bỏ qua trên thực tế. 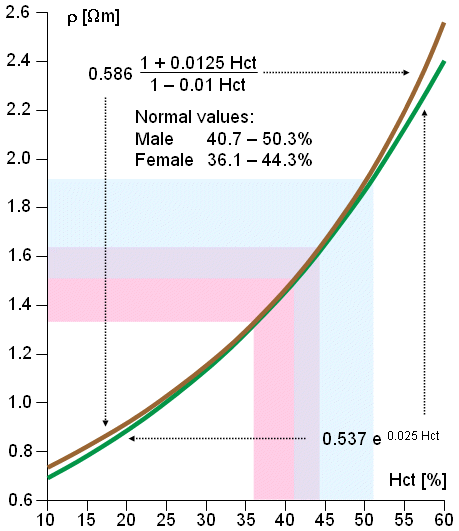Công thức 7.11 và 7.12 được biểu diễn trong hình 7.14.

Hình 7.4. Trở kháng của máu là một hàm của Hct. Công thức 7.11 và 7.12 được thể hiện dưới dạng biểu đồ

Mô hình hóa đầu ( Modeling the head )

Não được cấu tạo từ các mô thần kinh dễ bị kích thích. Về mặt điện học, sự hoạt động của nó có thể biểu diễn bằng điện não đồ (EEG). Mô não không chỉ là sự phân bố của các nguồn điện mà còn là một phần của bộ dẫn khối (bộ dẫn khối này bao gồm cả sọ và da đầu)

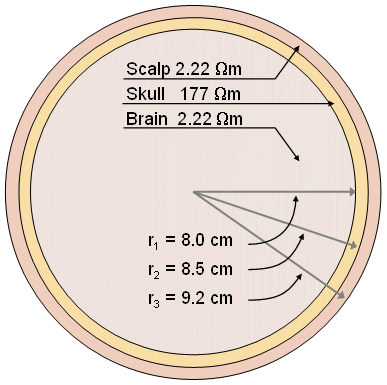
Xét về các mô hình bộ dẫn khối, đầu được xem như một chuỗi các vùng cầu đồng tâm như minh họa trong hình 7.5 (Rush và Driscoll, 1969). Trong mô hình này, bán kính bên trong và bên ngoài hộp sọ được chọn là 8 và 8,5 cm trong khi bán kính của đầu là 9,2 cm. Đối với não và da đầu, trở kháng được chọn là 2,22 Ωm trong khi trở kháng của sọ được gán giá trị là 80 × 2,22 Ωm = 177 Ωm. Do tính đối xứng và tính đơn giản, mô hình này dễ dàng được xây dựng giống như một mô hình bình điện phân hay mô hình máy tính và toán học. Chúng ta cũng có thể dễ dàng tính toán với các khối hình cầu. Dù mô hình đơn giản này không đề cập tới tính không đẳng hướng và không thuần nhất của mô não và xương vỏ não, nó cũng đưa ra kết quả phù hợp với các giá trị đo được.

Hình 7.5 . Mô hình đầu với các khối cầu đồng tâm. Mô hình này bao gồm vùng não, da đầu và sọ. Mỗi thành phần có thể được coi là thuần nhất.

Mô hình hóa ngực

Ứng dụng trong lĩnh vực điện sinh lí học được quan tâm nhiều nhất là điện tâm đồ. Nguồn điện được đặt hoàn toàn ở trong tim, trong khi bộ dẫn khối được cấu tạo từ tim và các cơ quan ở phần ngực. Rush, Abildskov và McFee (1963) đã giới thiệu 2 mô hình đơn giản về ngực. Trong cả 2 mô hình này, đường bao ngoài có hình dạng của phần ngực. Trong một mô hình đơn giản hơn, trở kháng của ngực được chọn là 10 Ωm. Trở kháng của máu trong tim được gán là 1 Ωm. Trong một mô hình chính xác hơn, trở kháng của phổi được chọn là 20 Ωm. Cùng với đó, các cơ tim và cơ liên sườn được mô hình hóa với trở kháng là 4 Ωm, máu trong tim được gán trở kháng là 1,6 Ωm, như mô tả trong hình 7.6. Vì trở kháng mô đo được trên thực nghiệm có một khoảng biến thiên đáng kể nên sẽ có một dải các giá trị được chọn để sử dụng trong các mô hình về ngực.

Trong mô hình điện não đồ bậc nhất, toàn bộ tim được coi như đồng nhất và có dạng cầu. Trong mô hình bậc 2, buồng tâm thất trái có thể được mô hình hóa bởi 1 hình cầu bán kính 5,6 cm và do đó, có thể tích là 736 cm³ và giả thuyết nó chứa đầy máu.

Trong những năm trở lại đây, một vài mô hình đã được phát triển, dựa trên cả 2 mô hình trên cũng như độ dẫn của tim, máu trong các khoang của tim, màng ngoài tim, phổi, các cơ bề mặt, mỡ, hình dạng bên ngoài của cơ thể. Một mô hình vật lý không thuần nhất và không đẳng hướng về phần thân người đã được xây dựng và mô tả bởi Rush (1971). Mô hình này cũng được Hyttinen sử dụng làm nền tảng cho mô hình máy tính.

Hình 7.6. Mô hình đơn giản về ngực của Rush (1971)

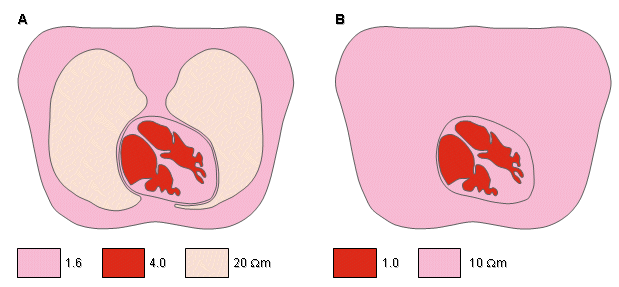
A. Các vùng tim, phổi và máu được phân biệt rõ ràng B. Vùng phổi được đồng nhất với tim và cơ bề mặt

Các bài toán thuận và ngược

Bài toán thuận

Bài toán mà trong đó nguồn và môi trường dẫn là đã biết trước nhưng trường chưa biết và cần phải xác định, được gọi là bài toán thuận. Bài toán thuận chỉ có 1 cách giải duy nhất. Người ta luôn có thể tính được trường với một độ chính xác nhất định nếu biết nguồn và bộ dẫn khối. Tuy nhiên, bài toán này khônng xảy ra trong các tình huống điều trị bệnh vì trong trường hợp này, trường có thể đo được ở bề mặt cơ thể.

Bài toán ngược

Bài toán trong đó trường và bộ dẫn điện đã biết trước nhưng nguồn lại không được biết thì được gọi là bài toán ngược (xem hình 7.7). Trong các ứng dụng y tế đối với các hiện tượng điện sinh học thì bài toán ngược có tầm quan trọng nhất định trong khám và điều trị bệnh. Ví như, trong chẩn đoán bệnh hàng ngày thì các bác sĩ chuyên khoa tim và các bác sĩ chuyên khoa thần kinh luôn phải tìm cách xác định nguồn gốc của các tín hiệu từ sinh học hoặc các tín hiệu điện sinh học đo được. Các bệnh lý tác động tới nguồn tạo nên nền tảng cho các nghiên cứu chẩn đoán của họ - đó là những trạng thái chẩn đoán của các bộ phận tương ứng. Tính khả thi cho việc tìm lời giải của bài toán ngược ra sao ? Điều này sẽ được đề cập ở phần tiếp theo.

Hình 7.7. Bài toán thuận và ngược

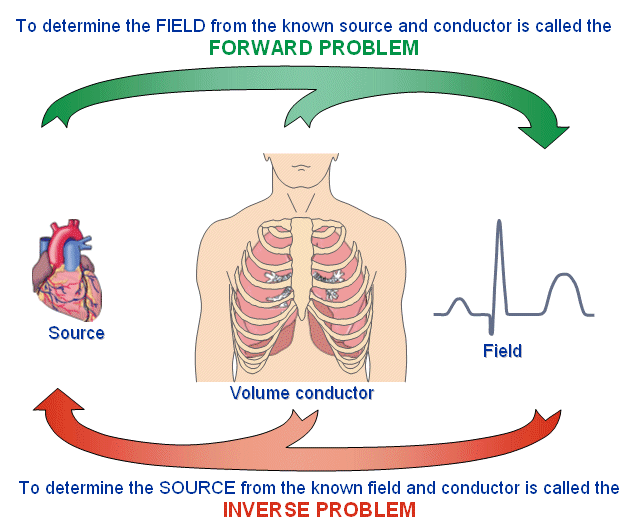
Khả năng giải quyết bài toán ngược

Chúng ta cùng xem xét khả năng giải bài toán ngược thông qua một ví dụ đơn giản về nguồn và bộ dẫn (hình 7.8). Trong mô hình này, nguồn được đặc trưng bởi một pin đơn và bộ dẫn là một mạng gồm 2 điện trở. Có 3 trường hợp trong đó nguồn điện áp được đặt tại các vị trí khác nhau trong mạng và có các giá trị khác nhau. Chú ý rằng: mặc dù biên độ của điện áp nguồn pin trong mỗi trường hợp là khác nhau, điện áp ra trong 3 trường hợp vẫn giống nhau, đều bằng 2 V.

Chúng ta có thể kiểm tra từng mạng bằng định lí Thevenin. Định lí chỉ ra rằng: luôn luôn có thể thay thế một tập hợp các nguồn điện áp và một mạch liên hợp bằng một nguồn tương đương đơn và trở kháng nối tiếp. Với định lí này, chúng ta có thể tính toán một mạng tương đương Thevenin cho 3 mạng ở trên. Trong mọi trường hợp, mạng tương đương được tính ra là giống nhau, sức điện động 2 V nối tiếp với trở kháng 4Ω. Điều này chứng tỏ rằng, dựa trên các phép đo ở bên ngoài, chúng ta chỉ có thể tính ra duy nhất một mạng Thevenin. Chúng ta đã chỉ ra rằng: mạng này tương ứng với cả 3 mạng có thực nhưng khác nhau. Ví dụ trên chỉ ra tính thiếu nhất quán trong việc tìm lời giải cho bài toán ngược.

Khả năng giải quyết bài toán ngược đã được bàn luận thông qua việc sử dụng một mạch điện đơn giản. Người đầu tiên phát biểu rằng: bài toán ngược không thể có một lời giải nhất quán là Hermann von Helmholtz (1853).

Hình 7.8 . Biểu hiện của sự thiếu nhất quán trong việc tìm lời giải của bài toán ngược

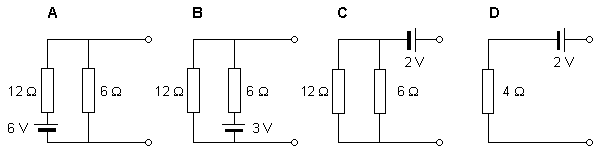
Các phương pháp khả thi đối với lời giải của bài toán ngược

Hoạt động điện tim (Cardiac electric activity) có thể đo được trên bề mặt vùng ngực và được gọi là điện tim đồ. Tương tự như vậy, điện cơ đồ, điện não đồ,... là các tín hiệu của các cơ, tế bào thần kinh và các bộ phân khác được đo trên bề mặt cơ thể người. Câu hỏi đặt ra với các bác sĩ là phải xác định nguồn gốc điện của các tín hiệu đo được và sau đó, quan sát xem các nguồn này là bình thường hay bất bình thường.

Xác định nguồn là lời giải của bài toán ngược. Như đã nhắc đến ở trên, không có lời giải duy nhất cho bài toán ngược. Vậy chúng ta có thể thắc mắc các bác sĩ chẩn đoán bệnh bằng cách nào. Mặc dù ở phần trước, ta đã nhắc đến tính thiếu nhất quán trong việc tìm lời giải bài toán ngược, tuy nhiên, vẫn có vài phương pháp để vượt qua vấn đề khó khăn này. Bốn phương pháp chủ yếu sẽ được đề cập ở dưới đây:

1. Phương pháp kinh nghiệm dựa trên sự thừa nhận một số mẫu tín hiệu chuẩn đã biết trước để kết hợp với các cấu trúc nguồn đã biết.

2. Tuân thủ các nghiêm luật của sinh lí học dựa trên các thông tin hữu ích về giải phẫu và sinh lí học của các mô hoạt động (active tissue). Phương pháp này phải tuân theo các giới hạn nghiêm ngặt về số lượng các giải pháp hữu hiệu.

3. Kiểm tra mẫu trường dẫn (the lead-field pattern) dựa vào độ nhạy của các đầu đo (lead) và do đó cấu trúc nguồn xác định theo tính thống kê có thể dự đoán được.

4. Mô hình hóa các nguồn và bộ dẫn khối bằng các mô hình được đơn giản hóa. Nguồn này được đặc trưng bởi các biến độc lập.

Chúng ta sẽ đề cập chi tiết hơn về các phương pháp này ở dưới đây:

Phương pháp kinh nghiệm

Phương pháp này dựa trên kinh nghiệm của các bác sĩ để nhận dạng một số mẫu tín hiệu đặc trưng liên quan tới một số triệu chứng rối loạn đã biết. Điều này có nghĩa là phép chẩn đoán dựa trên sự so sánh các mẫu tín hiệu thu được với một danh sách các mẫu liên quan tới những triệu chứng rối loạn bệnh lí. Nếu tín hiệu được nhận dạng thì phép chẩn đoán có thể được tiến hành. Quá trình này cũng chính thức sử dụng một biểu đồ chẩn đoán (diagnostic tree). Quá trình chẩn đoán được thực hiện một cách có trình tự thông qua một số bước, xuất phát từ cơ sở dữ liệu đã được thu thập. Do đó, chúng ta có thể xây dựng chương trình trên máy tính để tự động hóa quá trình chẩn đoán.

Tuân thủ các nghiêm luật của sinh lí học

Như đã đề cập đến ở trên, không có lời giải duy nhất cho bài toán ngược. Điều đó có nghĩa là một cấu trúc nguồn sẽ tạo ra nhiều trường tương ứng khi thực hiện các phép đo. Tuy nhiên, trong số nhiều lời giải, có thể chọn ra một lời giải đáp ứng đủ các tiêu chuẩn về mặt sinh lí học. Chúng ta nói rằng: quy trình này đòi hỏi phải tuân thủ các nghiêm luật của sinh lí học.

Phương pháp lí thuyết trường dẫn

Có thể xác định phân bố độ nhạy (sensitivity distribution) của các đầu đo (lead) . Chúng ta có thể xác định hoạt động của nguồn dựa trên những thông tin này. Đối với tất cả các đầu dò và các nguồn phân bố một cách thuần nhất, nguồn của tín hiệu dò được sẽ được xác định ở vùng mà độ nhạy của đầu dò là cao nhất. Nếu hệ thống đầu dò được thiết kế để dò các nguồn tương đương như lưỡng cực, mạng 4 cực , ... thì tín hiệu dò được sẽ đặc trưng cho các nguồn tương ứng với nó. Các nguồn này là mô hình được đơn giản hóa so với nguồn trên thực tế. Trong khi các mô hình được đơn giản hóa không nhất thiết phải là nguồn thì nó lại đăc trưng cho các cấu trúc chính của nguồn.

Mô hình nguồn được đơn giản hóa

Bài toán ngược có thể được giải quyết bằng việc mô hình hóa nguồn của tín hiệu điện sinh học hay từ sinh học và bộ dẫn khối theo các cách sau đây:

1. Một mô hình được xây dựng cho nguồn tín hiệu. Mô hình có một số giới hạn các biến độc lập nhưng vẫn phù hợp với tính giải phẫu và sinh lí của sự phân bố nguồn trên thực tế.

2. Một mô hình được xây dựng cho bộ dẫn khối. Độ chính xác của mô hình bộ dẫn phải bằng hoặc tốt hơn mô hình nguồn.

3. Các phép đo độc lập được thực hiện trong khi mô hình có nhiều biến độc lập. Bây giờ, chúng ta có những đẳng thức chưa biết và cần tính toán các biến của mô hình.

Trong phương pháp mô hình hóa,ta phải chú ý tới việc xem xét thực nghiệm. Đầu tiên, ta phải giảm độ nhạy đối với nhiễu, số phép đo độc lập tiến hành trên bề mặt cơ thể thường xuyên phải lớn hơn số biến trong mô hình nguồn. Các đẳng thức được giải dựa trên phép xấp xỉ bình phương tối thiểu (least squares approximation). Thứ hai, độ nhạy đối với nhiễu sẽ tăng khi ta tăng số biến độc lập. Chẳng hạn như, ta có thể thu được nhiều thông tin hơn khi sử dụng nhiều hơn các đa lưỡng cực nhưng kết quả có thể trở nên vô nghĩa khi ta tăng số lượng lên quá nhiều.

Tổng kết

Ở phần 7.5, chúng ta đã đề cập tới các vấn đề được quan tâm trong điện tim, điện não,... và lời giải cho bài toán ngược. Lời giải này liên quan tới việc xác định cấu trúc nguồn tương ứng với việc tạo ra tín hiệu điện đo được. Những kiến thức này giúp ta dễ dàng thực hiện các phép chẩn đoán.

Như đã chỉ ra ở phần trước, bài toán ngược không có lời giải duy nhất. Tuy nhiên, có thể dùng nhiều phương pháp xấp xỉ khác nhau để giải quyết bài toán. Dù việc tổng quát hóa vấn đề đến nay vẫn chưa thể thực hiện được nhưng đề tài này hiện đang được nghiên cứu khá nhiều.

Tài liệu tham khảo

Barber DC, Brown BH (1984): Applied potential tomography. J. Phys. E.: Sci. Instrum. 17: 723-33.

Epstein BR, Foster KR (1983): Anisotropy as a dielectric property of skeletal muscle. Med. & Biol. Eng. & Comput. 21:(1) 51-5.

Fricke H (1924): A mathematical treatment of the electric conductivity and capacity of disperse systems. Physiol. Rev. 4: 575-87. (Series 2).

Geddes LA, Baker LE (1967): The specific resistance of biological material - A compendium of data for the biomedical engineering and physiologist. Med. Biol. Eng. 5: 271-93.

Geddes LA, Sadler C (1973): The specific resistance of blood at body temperature. Med. Biol. Eng. 11:(5) 336-9.

Geselowitz DB (1963): The concept of an equivalent cardiac generator. Biomed. Sci. Instrum. 1: 325-30.

Geselowitz DB (1967): On bioelectric potentials in an inhomogeneous volume conductor. Biophys. J. 7:(1) 1-11.

Helmholtz HLF (1853): Ueber einige Gesetze der Vertheilung elektrischer Ströme in körperlichen Leitern mit Anwendung auf die thierisch-elektrischen Versuche. Ann. Physik und Chemie 89: 211-33, 354-77.

Horácek BM (1974): Numerical model of an inhomogeneous human torso. In Advances in Cardiology, Vol. 10, ed. S Rush, E Lepeshkin, pp. 51-7, S. Karger, Basel.

Hyttinen JA, Eskola HJ, Sievänen H, Malmivuo JA (1988): Atlas of the sensitivity distribution of the common ECG-lead systems. Tampere Univ. Techn., Inst. Biomed. Eng., Reports 2:(2) 25+67.

Liebman FM, Pearl J, Bagnol S (1962): The electrical conductance properties of blood in motion. Phys. Med. Biol. 7: 177-94.

Macfarlane PW, Lawrie TDV (1974): An Introduction to Automated Electrocardiogram Interpretation, 115 pp. Butterworths, London.

Malmivuo JA (1976): On the detection of the magnetic heart vector - An application of the reciprocity theorem. Helsinki Univ. Tech., Acta Polytechn. Scand., El. Eng. Series. Vol. 39., pp. 112. (Dr. tech. thesis)

McFee R, Baule GM (1972): Research in electrocardiography and magnetocardiography. Proc. IEEE 60:(3) 290-321.

Pilkington TC, Plonsey R (1982): Engineering Contributions to Biophysical Electrocardiography, 248 pp. IEEE Press, John Wiley, New York.

Plonsey R (1969): Bioelectric Phenomena, 380 pp. McGraw-Hill, New York.

Plonsey R, Heppner DB (1967): Considerations of quasistationarity in electrophysiological systems. Bull. Math. Biophys. 29:(4) 657-64.

Rudy Y, Plonsey R (1979): The eccentric spheres model as the basis of a study of the role of geometry and inhomogeneities in electrocardiography. IEEE Trans. Biomed. Eng. BME-26:(7) 392-9.

Rush S (1971): An inhomogeneous anisotropic model of the human torso for electrocardiographic studies. Med. Biol. Eng. 9:(5) 201-11.

Rush S, Abildskov JA, McFee R (1963): Resistivity of body tissues at low frequencies. Circulation 22:(1) 40-50.

Rush S, Driscoll DA (1969): EEG-electrode sensitivity - An application of reciprocity. IEEE Trans. Biomed. Eng. BME-16:(1) 15-22.

Saha S, Williams PA (1992): Electric and dielectric properties of wet human cortical bone as a function of frequency. IEEE Trans. Biomed. Eng. 39:(12) 1298-304.

Schwan HP, Kay CF (1956): Specific resistance of body tissues. Circ. Res. 4:(6) 664-70.

Schwan HP, Kay CF (1957): Capacitive properties of body tissues. Circ. Res. 5:(4) 439-43.

Smyth WR (1968): Static and Dynamic Electricity, 3rd ed., 623 pp. McGraw-Hill, New York.

Stratton JA (1941): Electromagnetic Theory, McGraw-Hill, New York.

Stuchly MA, Stuchly SS (1984): Electrical properties of biological substance. In Biological Effects and Medical Applications of Electromagnetic Fields, ed. OP Gandhi, Academic Press, New York.

Tanaka K, Kanai H, Nakayama K, Ono N (1970): The impedance of blood: The effects of red cell orientation and its application. Jpn. J. Med. Eng. 8: 436-43.

Wikswo JP, Swinney KR (1984): Comparison of scalar multipole expansions. J. Appl. Phys. 56:(11) 3039-49.

---

trang trước

Nguồn khối và bộ dẫn khối

Trang tiếp

Liên kết đến đây

• Sách:Điện từ sinh học
• Sách:Điện từ sinh học/Mô hình nguồn trường
• Sách:Điện từ sinh học/Các nguồn và bộ dẫn điện sinh học và mô hình của chúng