Chủ đề nóng: Phương pháp kỷ luật tích cực - Cổ học tinh hoa - Những thói hư tật xấu của người Việt - Công lý: Việc đúng nên làm - Giáo án Điện tử - Sách giáo khoa - Học tiếng Anh - Bài giảng trực tuyến - Món ăn bài thuốc - Chăm sóc bà bầu - Môi trường - Tiết kiệm điện - Nhi khoa - Ung thư - Tác hại của thuốc lá - Các kỹ thuật dạy học tích cực
- Dạy học phát triển năng lực - Chương trình giáo dục phổ thông
Tính lãi tiết kiệm ngân hàng
Từ VLOS
Đôi khi, để tính lãi thu được từ tài khoản tiết kiệm, ta chỉ việc lấy lãi suất nhân với số tiền gốc. Tuy nhiên, trong hầu hết trường hợp, nó lại không dễ dàng như vậy. Chẳng hạn như, nhiều tài khoản tiết kiệm được niêm yết với lãi suất kỳ hạn một năm nhưng lại được gộp lãi hàng tháng. Mỗi tháng, một phần lãi sẽ được tính và cộng dồn vào tiền gốc, ảnh hưởng đến lãi của những tháng sau. Việc tăng dần và liên tục cộng thêm vào tiền gốc được gọi là ghép lãi và cách dễ nhất để tính số tiền thu được trong tương lai là dùng công thức lãi kép. Hãy đọc tiếp để hiểu thêm về ưu và nhược điểm của cách tính lãi này.
Mục lục
Các bước[sửa]
Tính lãi kép[sửa]
-
Nhận
biết
công
thức
tính
tác
động
của
lãi
kép.
Đó
là:
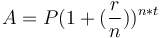 .
.
- (P) là số tiền gốc, (r) là lãi suất kỳ hạn một năm và (n) là số lần lãi được cộng gộp trong năm. (A) là số dư tài khoản tính toán dưới tác động của lãi kép.
- (t) là thời gian lãi được tích lũy. Con số này nên phù hợp với lãi suất sử dụng (chẳng hạn như nếu lãi suất được tính theo năm thì (t) nên là số hay phần của năm). Nếu nhỏ hơn một năm, hãy lấy tổng số tháng chia cho 12 hoặc tổng số ngày chia cho 365.
-
Xác
định
biến
sử
dụng
trong
công
thức.
Xem
lại
điều
khoản
tài
khoản
tiết
kiệm
cá
nhân
hoặc
liên
hệ
với
đại
diện
ngân
hàng
để
nhập
giá
trị
vào
phương
trình.
- Vốn gốc (P) là khoản tiền gửi ban đầu hoặc số tiền hiện có được dùng để tính lãi.
- Lãi suất (r) nên được để dưới dạng thập phân. 3% nên được điền vào công thức dưới dạng 0,03. Để có con số này, bạn chỉ việc chia 3 cho 100.
- Giá trị (n) là số lần lãi được tính và gộp vào tiền gốc (ghép lãi) trong một năm. Phổ biến nhất là ghép lãi theo tháng (n=12), quý (n=4) và năm (n=1). Tuy nhiên, vẫn có thể tồn tại một số lựa chọn khác, tùy vào điều khoản cụ thể trong tài khoản tiết kiệm của bạn.[1]
-
Thay
giá
trị
vào
công
thức.
Một
khi
đã
xác
định
được
giá
trị
từng
biến
số,
hãy
điền
vào
công
thức
lãi
kép
để
tìm
lãi
thu
được
qua
khung
thời
gian
cụ
thể.
Ví
dụ,
với
P=
20.000.000
đồng,
r=0,05
(5%),
n=4
(gộp
lãi
theo
quý)
và
t=1
năm,
ta
có
phương
trình
sau:
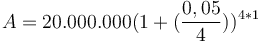 đồng.
đồng.
- Lãi gộp theo ngày cũng được tính theo cách tương tự, chỉ khác ở chỗ trong trường hợp này, biến (n) là 365 thay vì 4 như ở trên.[2]
-
Tiến
hành
tính
toán.
Giờ
đây,
khi
giá
trị
đã
được
thế
vào,
hãy
cùng
giải
phương
trình.
Bắt
đầu
bằng
cách
rút
gọn
những
phần
đơn
giản
trước.
Nó
bao
gồm
chia
lãi
suất
năm
cho
số
kỳ
để
có
được
lãi
theo
kỳ
(trong
trường
hợp
này,
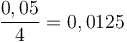 )
và
tìm
)
và
tìm
 ,
ở
đây
đơn
giản
là:
,
ở
đây
đơn
giản
là:
 .
Từ
đó,
ta
thu
được
phương
trình:
.
Từ
đó,
ta
thu
được
phương
trình:
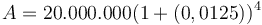 đồng.
đồng.
-
Phương
trình
này
có
thể
được
rút
gọn
thêm
bằng
cách
thực
hiện
phép
tính
có
trong
dấu
ngoặc:
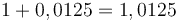 .
Giờ,
ta
được:
.
Giờ,
ta
được:
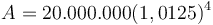 đồng.
đồng.
-
Phương
trình
này
có
thể
được
rút
gọn
thêm
bằng
cách
thực
hiện
phép
tính
có
trong
dấu
ngoặc:
-
Giải
phương
trình.
Tiếp
đến,
tính
lũy
thừa
bằng
cách
lấy
kết
quả
thu
được
ở
bước
cuối
lũy
thừa
cho
bốn
(nghĩa
là
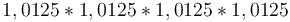 ).
Ta
được
).
Ta
được
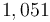 .
Phương
trình
chỉ
còn
đơn
giản
là:
.
Phương
trình
chỉ
còn
đơn
giản
là:
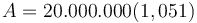 đồng.
Nhân
hai
số
này
với
nhau
để
có:
đồng.
Nhân
hai
số
này
với
nhau
để
có:
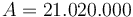 đồng.
Đây
là
giá
trị
tài
khoản
tiết
kiệm
của
bạn
sau
một
năm
với
lãi
suất
5%
(gộp
lãi
hàng
quý).
đồng.
Đây
là
giá
trị
tài
khoản
tiết
kiệm
của
bạn
sau
một
năm
với
lãi
suất
5%
(gộp
lãi
hàng
quý).
-
Lưu
ý
rằng
con
số
này
cao
hơn
đôi
chút
so
với
kết
quả
mà
có
thể
bạn
sẽ
kỳ
vọng
nhận
được
khi
lãi
suất
theo
năm
được
niêm
yết
-
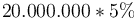 đồng.
Nó
cho
thấy
sự
quan
trọng
trong
việc
hiểu
cách
thức
và
thời
điểm
lãi
được
cộng
gộp!
đồng.
Nó
cho
thấy
sự
quan
trọng
trong
việc
hiểu
cách
thức
và
thời
điểm
lãi
được
cộng
gộp! -
Lãi
thu
được
là
chênh
lệch
giữa
A
và
B.
Vậy
tổng
lãi
thu
được
là
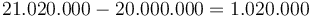 đồng.
đồng.
-
Lưu
ý
rằng
con
số
này
cao
hơn
đôi
chút
so
với
kết
quả
mà
có
thể
bạn
sẽ
kỳ
vọng
nhận
được
khi
lãi
suất
theo
năm
được
niêm
yết
-
Tính lãi với góp vốn thường xuyên[sửa]
-
Đầu
tiên,
hãy
sử
dụng
công
thức
tiết
kiệm
tích
lũy.
Bạn
cũng
có
thể
tính
lãi
suất
thu
được
trên
tài
khoản
góp
vốn
hàng
tháng.
Nó
hữu
dụng
nếu
lượng
tiền
mà
bạn
tiết
kiệm
được
ổn
định
và
được
chuyển
vào
tài
khoản
tiết
kiệm
mỗi
tháng.
Phương
trình
đầy
đủ
là:
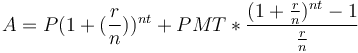 [3]
[3]
- Một phương pháp đơn giản khác là tách biệt phần lãi kép của vốn gốc với phần lãi thu được từ vốn góp (hay khoản thanh toán/PMT). Để bắt đầu, hãy tính lãi vốn gốc bằng công thức tiết kiệm tích lũy.
- Có thể thấy, với công thức này, bạn có thể tính lãi thu được trên tài khoản tiết kiệm được gửi thêm hàng tháng và lãi ghép theo ngày, tháng hoặc quý.[3]
- Dùng thành phần thứ hai trong công thức để tính lãi của vốn góp. (PMT) đại diện cho lượng vốn góp hàng tháng.
-
Xác
định
biến
số.
Kiểm
tra
thỏa
thuận
đầu
tư
hay
tiết
kiệm
của
bạn
để
tìm
những
biến
sau:
vốn
gốc
"P",
lãi
suất
năm
"r"
và
số
kỳ
trong
năm
"n".
Nếu
không
có
sẵn,
hãy
liên
hệ
ngân
hàng
của
bạn.
Biến
"t"
đại
diện
cho
số
năm
hay
phần
của
năm
được
dùng
để
tính
lãi
và
"PMT"
là
giá
trị
góp
vốn/thanh
toán
mỗi
tháng.
"A"
là
tổng
giá
trị
tài
khoản
thu
được
với
thời
gian
và
vốn
góp
cho
trước.
- Vốn gốc "P" cũng có thể đại diện cho giá trị tài khoản tại thời điểm được chọn bắt đầu tính lãi.
- Lãi suất "r" cho biết lãi được trả cho tài khoản mỗi năm. Nó nên được thể hiện ở dạng thập phân trong công thức. Nghĩa là, lãi suất 3% nên được biểu diễn dưới dạng 0,03. Để có số thập phân này, bạn chỉ việc lấy lãi suất ở dạng phần trăm chia cho 100.
- "n" chỉ đơn giản là số lần ghép lãi trong một năm. Đó sẽ là 365 nếu ghép theo ngày, 12 nếu theo tháng và 4 trong trường hợp theo quý.
- Tương tự, "t" đại diện cho số năm được dùng để tính lãi. Đó có thể là số năm hoặc phần của năm nếu thời gian tính lãi ít hơn một năm (ví dụ 0,0833 (1/12) cho thời gian 1 tháng).[1]
-
Thay
giá
trị
vào
công
thức.
Với
P=20.000.000
đồng,
r=0,05
(5%),
n=12
(ghép
lãi
theo
tháng),
t=3
năm
và
PMT=2.000.000
đồng,
ta
thu
được:
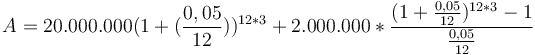 đồng.
đồng. -
Rút
gọn
phương
trình.
Bắt
đầu
với
việc
rút
gọn
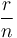 ,
có
thể
là
bằng
cách
lấy
lãi
suất
0,05
chia
cho
12.
Ta
được:
,
có
thể
là
bằng
cách
lấy
lãi
suất
0,05
chia
cho
12.
Ta
được:
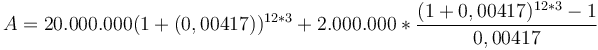 .
Bạn
cũng
có
thể
rút
gọn
bằng
cách
cộng
thêm
một
vào
lãi
suất
nằm
trong
dấu
ngoặc.
Phương
trình
thu
được
sẽ
là:
.
Bạn
cũng
có
thể
rút
gọn
bằng
cách
cộng
thêm
một
vào
lãi
suất
nằm
trong
dấu
ngoặc.
Phương
trình
thu
được
sẽ
là:
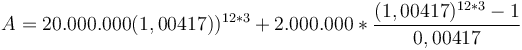 đồng
đồng -
Tính
lũy
thừa.
Đầu
tiên,
tìm
số
mũ:
 .
Ta
được
.
Ta
được
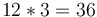 .
Tiếp
đến,
lũy
thừa
để
rút
gọn
phương
trình
thành
.
Tiếp
đến,
lũy
thừa
để
rút
gọn
phương
trình
thành
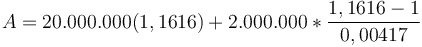 đồng.
Rút
gọn
bằng
cách
trừ
bớt
cho
1,
ta
được
đồng.
Rút
gọn
bằng
cách
trừ
bớt
cho
1,
ta
được
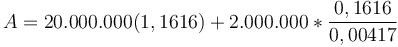 đồng.
đồng. -
Tiến
hành
thực
hiện
những
phép
tính
cuối
cùng.
Nhân
cụm
đầu
của
phương
trình,
ta
thu
được
32.320.000
đồng.
Tính
cụm
còn
lại
bằng
cách
chia
mẫu
số
cho
tử
số:
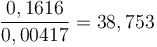 .
Tiếp
đến,
nhân
kết
quả
thu
được
cho
giá
trị
vốn
góp
(trong
trường
hợp
này
là
2.000.000
đồng).
Phương
trình
thu
được
là:
.
Tiếp
đến,
nhân
kết
quả
thu
được
cho
giá
trị
vốn
góp
(trong
trường
hợp
này
là
2.000.000
đồng).
Phương
trình
thu
được
là:
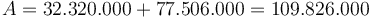 đồng.
Giá
trị
tài
khoản
tiết
kiệm
với
những
điều
khoản
này
sẽ
là
đồng.
Giá
trị
tài
khoản
tiết
kiệm
với
những
điều
khoản
này
sẽ
là
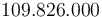 đồng.
đồng. -
Tính
tổng
lãi
thu
được.
Trong
phương
trình
này,
lãi
thu
được
là
hiệu
giữa
tổng
tài
khoản
(A)
với
tổng
của
vốn
gốc
(P)
và
tích
giữa
số
lần
góp
vốn
và
giá
trị
góp
vốn
(PMT*n*t).
Trong
ví
dụ
trên,
lãi
suất
thu
được
chính
bằng
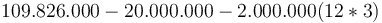 hay
hay
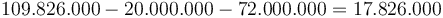 đồng.[3]
đồng.[3]
Dùng bảng tính để tính lãi ghép[sửa]
- Mở một bảng tính mới. Excel hoặc những chương trình bảng tính tương tự (chẳng hạn như Google Sheets) giúp bạn tiết kiệm thời gian tính toán và thậm chí có cung cấp những lối tắt dưới dạng hàm tài chính đã được thiết kế sẵn nhằm hỗ trợ tính lãi ghép.
- Đặt tên biến. Khi dùng bảng tính, sắp xếp mọi thứ ngay ngắn và rõ ràng hết mức có thể sẽ luôn hữu ích. Hãy bắt đầu đặt tên cho cột những ô chứa thông tin quan trọng được dùng trong tính toán của bạn (ví dụ: lãi suất, vốn gốc, thời gian, n, vốn góp).
- Cho biến vào bảng tính. Bây giờ, hãy điền dữ liệu của tài khoản vào cột tiếp theo. Nhờ đó, bảng tính không chỉ dễ nhìn và diễn dịch về sau mà còn cho phép thay đổi một hay nhiều biến để có thể nghiên cứu nhiều phương án tiết kiệm khác nhau.
-
Lập
phương
trình.
Bước
tiếp
theo
là
gõ
vào
phiên
bản
công
thức
lãi
tích
lũy
của
chính
bạn
(
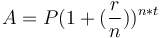 )
hoặc
phiên
bản
phức
tạp
hơn,
có
tính
đến
góp
vốn
hàng
tháng
(
)
hoặc
phiên
bản
phức
tạp
hơn,
có
tính
đến
góp
vốn
hàng
tháng
(
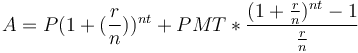 ).
Dùng
bất
kỳ
ô
trắng
nào,
bắt
đầu
với
"="
và
sử
dụng
ký
hiệu
toán
học
thông
thường
(kể
cả
dấu
ngoặc
nếu
cần)
để
đánh
phương
trình
thích
hợp.
Thay
vì
nhập
biến
như
(P)
và
(n),
hãy
đánh
tên
ô
lưu
trữ
dữ
liệu
tương
ứng
hoặc
đơn
giản
là
nhấp
chuột
vào
những
ô
đó
khi
soạn
phương
trình.
).
Dùng
bất
kỳ
ô
trắng
nào,
bắt
đầu
với
"="
và
sử
dụng
ký
hiệu
toán
học
thông
thường
(kể
cả
dấu
ngoặc
nếu
cần)
để
đánh
phương
trình
thích
hợp.
Thay
vì
nhập
biến
như
(P)
và
(n),
hãy
đánh
tên
ô
lưu
trữ
dữ
liệu
tương
ứng
hoặc
đơn
giản
là
nhấp
chuột
vào
những
ô
đó
khi
soạn
phương
trình. -
Dùng
hàm
tài
chính.
Excel
cũng
cung
cấp
những
hàm
tài
chính
có
thể
hỗ
trợ
việc
tính
toán
của
bạn.
Đặc
biệt,
"giá
trị
tương
lai"
(future
value
-
FV)
có
thể
được
dùng
bởi
nó
tính
giá
trị
của
một
tài
khoản
tại
một
thời
điểm
nào
đó
trong
tương
lai
với
những
biến
giống
như
những
biến
mà
bạn
đang
làm
quen.
Để
sử
dụng
hàm
này,
hãy
đi
đến
bất
kỳ
ô
trắng
nào
và
gõ
"=FV(".
Excel
sẽ
có
cửa
sổ
hướng
dẫn
ngay
khi
bạn
mở
ngoặc
công
thức
hàm
đầu
tiên
nhằm
hỗ
trợ
việc
nhập
đúng
tham
số.
[4]
-
Thay
vì
cộng
dồn
lãi
thu
được,
hàm
giá
trị
tương
lai
được
thiết
kế
nhằm
tính
số
tiền
phải
trả
để
cân
bằng
tài
khoản
hiện
có
khi
tài
khoản
này
liên
tục
tích
lãi.
Do
đó,
hàm
sẽ
tự
động
đưa
ra
kết
quả
âm.
Để
giải
quyết
vấn
đề
này,
hãy
gõ
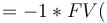
-
Những
tham
số
dữ
liệu
tương
tự,
tách
biệt
bằng
dấu
phẩy,
được
dùng
trong
hàm
FV
nhưng
chúng
không
thật
sự
đồng
nhất
với
những
tham
số
mà
ta
đã
dùng
ở
trên.
Ví
dụ,
"lãi
suất"
ở
đây
là
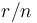 (lãi
suất
năm
chia
cho
"n").
Nó
sẽ
được
tính
tự
động
trong
phần
dấu
ngoặc
của
hàm
FV.
(lãi
suất
năm
chia
cho
"n").
Nó
sẽ
được
tính
tự
động
trong
phần
dấu
ngoặc
của
hàm
FV. -
Tham
số
"nper"
ở
đây
là
biến
 -
tổng
số
kỳ
lãi
được
cộng
gộp
và
tổng
số
lần
góp
vốn.
Hay
nói
cách
khác,
nếu
PMT
khác
không,
hàm
FV
sẽ
mặc
định
rằng
bạn
góp
lượng
vốn
PMT
qua
mỗi
và
mọi
kỳ
được
xác
định
bởi
"nper".
-
tổng
số
kỳ
lãi
được
cộng
gộp
và
tổng
số
lần
góp
vốn.
Hay
nói
cách
khác,
nếu
PMT
khác
không,
hàm
FV
sẽ
mặc
định
rằng
bạn
góp
lượng
vốn
PMT
qua
mỗi
và
mọi
kỳ
được
xác
định
bởi
"nper". - Lưu ý rằng phương trình này phổ biến nhất cho (những tính toán như) tính lịch trả nợ vay thế chấp qua thời gian với thanh toán định kỳ. Ví dụ, nếu dự định trả góp hàng tháng trong vòng 5 năm, "nper" sẽ là 60 (5 năm * 12 tháng).
- PMT là lượng góp vốn định kỳ trong suốt toàn bộ thời gian (một phần vốn góp trên "n").
- "[pv]" (hay Giá trị Hiện tại) là tài khoản vốn gốc - số dư ban đầu tài khoản của bạn.
- Biến cuối cùng, "[type]" (loại), có thể được để trống trong công thức tính toán này (khi đó, hàm tự đưa nó về 0).
-
Hàm
FV
cho
phép
bạn
thực
hiện
những
tính
toán
đơn
giản
bên
trong
dấu
ngoặc
của
công
thức
hàm,
chẳng
hạn
như
một
hàm
FV
hoàn
chỉnh
có
thể
sẽ
có
dạng
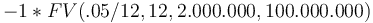 .
Nó
cho
thấy
mức
lãi
năm
5%
được
ghép
hàng
tháng
trong
kỳ
hạn
12
tháng
và
trong
thời
gian
đó,
bạn
góp
vốn
2.000.000
đồng/tháng.
Đồng
thời,
số
dư
ban
đầu
(vốn
gốc)
của
bạn
là
100.000.000
đồng.
Kết
quả
thu
được
cho
biết
tài
khoản
có
sau
1
năm
của
bạn
là
bao
nhiêu
(129.674.000
đồng).
.
Nó
cho
thấy
mức
lãi
năm
5%
được
ghép
hàng
tháng
trong
kỳ
hạn
12
tháng
và
trong
thời
gian
đó,
bạn
góp
vốn
2.000.000
đồng/tháng.
Đồng
thời,
số
dư
ban
đầu
(vốn
gốc)
của
bạn
là
100.000.000
đồng.
Kết
quả
thu
được
cho
biết
tài
khoản
có
sau
1
năm
của
bạn
là
bao
nhiêu
(129.674.000
đồng).
-
Thay
vì
cộng
dồn
lãi
thu
được,
hàm
giá
trị
tương
lai
được
thiết
kế
nhằm
tính
số
tiền
phải
trả
để
cân
bằng
tài
khoản
hiện
có
khi
tài
khoản
này
liên
tục
tích
lãi.
Do
đó,
hàm
sẽ
tự
động
đưa
ra
kết
quả
âm.
Để
giải
quyết
vấn
đề
này,
hãy
gõ
Lời khuyên[sửa]
- Bên cạnh đó, tính lãi ghép có thể sẽ phức tạp hơn với góp vốn không cố định. Lúc này, bạn cần tính lãi từng lần góp vốn/thanh toán một cách riêng lẻ (với cùng công thức được giới thiệu ở trên) và tốt nhất là nên sử dụng bảng tính để đơn giản hóa việc tính toán.
- Bạn cũng có thể sử dụng công cụ tính lãi công bố hàng năm trực tuyến để xác định lãi thu được từ tài khoản tiết kiệm. Hãy tìm kiếm trên mạng cụm từ "công cụ tính lãi công bố hàng năm" để có được vô số trang cung cấp dịch vụ miễn phí này.
Nguồn và Trích dẫn[sửa]
- ↑ 1,0 1,1 https://qrc.depaul.edu/StudyGuide2009/Notes/Savings%20Accounts/Compound%20Interest.htm
- ↑ http://www.mymoneyblog.com/interest_compou.html
- ↑ 3,0 3,1 3,2 http://www.thecalculatorsite.com/articles/finance/compound-interest-formula.php
- ↑ https://support.office.com/en-us/article/FV-function-2eef9f44-a084-4c61-bdd8-4fe4bb1b71b3






