Thảo luận:Đại số 10/Chương II/§1. Hàm số
Mục lục
Mục tiêu[sửa]
Xem chi tiết tại: Đại số 10/Chuẩn kiến thức và kĩ năng#1. Đại cương về hàm số
Nắm vững các khái niệm hàm số, tập xác định, đồ thị và các khái niệm đồng biến, nghịch biến, hàm số chẵn, hàm số lẻ, đồng thời biết cách tìm tập xác định và cách lập bảng biến thiên một hàm số đơn giản.
Nội dung[sửa]
Ôn tập về hàm số[sửa]
Khái niệm hàm số[sửa]
Xem thêm tại: Đại số 10/Chuẩn kiến thức và kĩ năng#Cách trình bày
Ở lớp 7 và lớp 9 học sinh đã biết về hàm số như một khái niệm Toán học mô tả sự phụ thuộc lẫn nhau giữa hai đại lượng biến thiên.
SGK Đại số 10 nhắc lại định nghĩa hàm số ở lớp 9 và đưa thêm khái niệm tập xác định D, là tập mà trên đó đại lượng x nhận giá trị.
Như vậy, khái niệm hàm số được nhắc lại và chính xác hóa từ định nghĩa đã học ở lớp 7 và 9.
Giáo viên nên thay đổi và cập nhật các ví dụ hàm số theo tình hình kinh tế và xã hội của đất nước (dựa theo ví dụ đã nêu trong SGK).
Hoạt động 1, nhằm khuyến khích học tự tìm các ví dụ về hàm số để các em thấy ý nghĩa thực tiễn của khái niệm này (nên yêu cầu các em chuẩn bị trước ở nhà).
Cách cho hàm số[sửa]
Một hàm số có thể được cho bằng bảng, biểu đồ hoặc bằng công thức. Chú ý rằng trong các SGK Toán thường chỉ xét các hàm số được cho bởi công thức, tuy nhiên trong thực tế lại thường gặp các hàm số cho bởi bảng hoặc biểu đồ.
Với cách cho hàm số bằng bảng và biểu đồ, SGK cố gắng đưa ra những ví dụ thực tế về hàm số và qua các ví dụ này củng cố khái niệm tập xác định của hàm số, khái niệm giá trị của hàm số.
Học sinh đã biết nhiều hàm số được cho bởi công thức trong SGK Toán Trung học cơ sở. Điểm mới cần nhấn mạnh ở đây là quy ước về tập xác định của hàm số được cho bởi công thức. Sau quy ước này là những bài tập tìm tập xác định của một hàm số.
Hoạt động 6, nhằm làm cho học sinh làm quen với các hàm số được cho bởi nhiều biểu thức.
-
-
-
CHÚ
Ý
- Trong công thức y = f(x), thì f(x) được gọi là biểu thức của hàm số. Khi viết y = 2x - 1 thì ta hiểu biểu thức f(x) = 2x - 1.
-
Do
đó,
hai
cách
viết
sau
là
như
nhau:
- y = 2x - 1
- f(x) = 2x -1
-
CHÚ
Ý
-
Đồ thị của hàm số[sửa]
Học sinh đã biết khái niệm đồ thị của hàm số từ lớp 7, do đó ở đây chỉ nhắc lại định nghĩa và nêu lại hai dạng dồ thị của hàm số y = ax và y = ax2 đã biết ở lớp 9.
Hoạt động 7, để học sinh tập "đọc" đồ thị (đọc xuôi, đọc ngược), nghĩa là dựa vào đồ thị để tìm f(x) theo các giá trị của x và ngược lại tìm x theo f(x).
Chẳng hạn, để tìm f(-2), từ điểm -2 trên trục hoành ta kẻ một đường song song với trục Oy cắt đồ thị tại điểm M. Từ điểm M kẻ đường song song với trục Ox, cắt trục tung tại điểm -1. Ta được f(-2) = -1.
Sự biến thiên của hàm số[sửa]
Khái niệm đồng biến, nghịch biến cũng đã được trình bày trong SGK Toán 9.
Phần mới ở đây là đưa ra bảng biến thiên để tổng kết kết quả xét chiều biến thiên của một hàm số.
Đồng biến, nghịch biến[sửa]
Khái niệm đồng biến, nghịch biến được đưa ra bắt đầu từ nhận xét trực giác về đồ thị của hàm số y = x2 trong các khoảng và . Định nghĩa của khái niệm này có hai cách diễn đạt:
-
Cách
thứ
nhất:
"
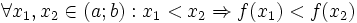 (hoặc
(hoặc
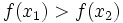 )".
)".
-
Cách
thứ
hai:
"
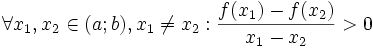 (hoặc
(hoặc
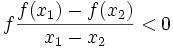 )".
)".
Cách thứ nhất trực quan dễ hiểu, cách thứ hai rất thuận tiện trong thực hành. Tuy nhiên, đối với chương trình GDTHPT môn Toán lớp 10, ta chỉ nêu cách diễn đạt thứ nhất.
Bảng biến thiên[sửa]
Khi lập bảng biến thiên của một hàm số, cần xét xem giá trị của hàm số tại lân cận của các đầu mút của khoảng biến thiên.
- Chẳng hạn, hàm số y = x2 xác định trên khoảng (-∞;+∞), khi x dần tới -∞ hoặc +∞ thì y đều dần tới +∞.
Khái niệm dần tới -∞, +∞, được giới thiệu dưới dạng một chú ý cuối mục 1 (vì học sinh chưa biết khái niệm giới hạn).
Tính chẵn, lẻ của hàm số[sửa]
Khái niệm hàm số chẵn, hàm số lẻ cũng được đưa ra từ nhận xét trực giác về đồ thị của hàm số và hàm số y = x. Trong định nghĩa về tính chẵn lẻ của hàm số cần chú ý yêu cầu tập xác định D của hàm số phải có tính chất:
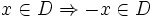 tui
gọi
nó
là
tính
chất
đối
xứng
của
tập
xác
định
tui
gọi
nó
là
tính
chất
đối
xứng
của
tập
xác
địnhTrong hoạt động 8 ta có kết quả như sau:
a)
Tập
xác
định
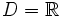 thỏa
mãn
yêu
cầu
thỏa
mãn
yêu
cầu
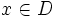 thì
thì
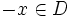 và
và
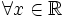 ,
y
=
f(x)
=
3x2
-
2
=
3(-x)2
-
2
=
f(x).
Vậy
hàm
số
y
=
3x2
-
2
là
hàm
số
chẵn.
,
y
=
f(x)
=
3x2
-
2
=
3(-x)2
-
2
=
f(x).
Vậy
hàm
số
y
=
3x2
-
2
là
hàm
số
chẵn.
b)
Tập
xác
định
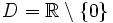 thỏa
mãn
yêu
cầu
thỏa
mãn
yêu
cầu
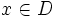 thì
thì
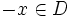 và
và
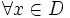 ,
,
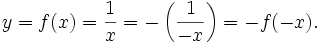 Vậy
hàm
số
Vậy
hàm
số
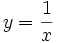 là
hàm
số
lẻ.
là
hàm
số
lẻ.
c)
Tập
xác
định
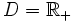 (trong
đó
(trong
đó
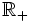 là
tập
hợp
các
số
thực
dương
và
số
0)
không
thỏa
mãn
yêu
cầu
là
tập
hợp
các
số
thực
dương
và
số
0)
không
thỏa
mãn
yêu
cầu
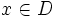 thì
thì
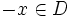 .
Do
đó
hàm
số
không
là
hàm
số
chẵn,
cũng
không
là
hàm
số
lẻ.
.
Do
đó
hàm
số
không
là
hàm
số
chẵn,
cũng
không
là
hàm
số
lẻ.


