Phạm Thạch Thảo
Chủ đề nóng: Giáo án Điện tử • Sách giáo khoa • Học tiếng Anh • Bài giảng trực tuyến • Công lý: Việc đúng nên làm • Món ăn bài thuốc • Chăm sóc bà bầu • Môi trường • Tiết kiệm điện
Đại số 9/Chương II/§1. Nhắc lại và bổ sung các khái niệm về hàm số
Bài từ Tủ sách Khoa học VLOS
Mục lục |
Lí thuyết
Khái niệm hàm số
Các mục 1, 2, 4, 5: xem Đại số 7/Chương II/§5. Hàm số#Khái niệm hàm số
3. Khi hàm số cho bởi công thức y = f(x), ta hiểu rằng biến số x chỉ lấy những giá trị mà tại đó f(x) xác định.
- Chẳng hạn, ở các ví dụ trên, giá trị của các biểu thức 2x, 2x + 3 luôn luôn xác định với mọi giá trị của x nên trong các hàm số y = 2x và y = 2x + 3, biến số x có thể lấy những giá trị tùy ý.
- Còn trong hàm số
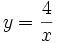, biến số x chỉ lấy những giá trị khác 0, vì giá trị của biểu thức 
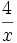không xác định khi x = 0.
- Còn trong hàm số
Đồ thị của hàm số
Hàm số đồng biến, nghịch biến
Một cách tổng quát
Cho hàm số y = f(x) xác định với mọi giá trị của x thuộc R.
a) Nếu giá trị của biến x tăng lên mà giá trị tương ứng f(x) cũng tăng lên thì hàm số y = f(x) được gọi là hàm số đồng biến trên R (gọi tắt là hàm số đồng biến). b) Nếu giá trị của biến x tăng lên mà giá trị tương ứng f(x) lại giảm xuống thì hàm số y = f(x) được gọi là hàm số nghịch biến trên R (gọi tắt là hàm số nghịch biến). Nói cách khác, với mọi x1, x2 bất kì thuộc R. Nếu x1 < x2 mà f(x1) < f(x2) thì hàm số y = f(x) đồng biến trên R. Nếu x1 < x2 mà f(x1) > f(x2) thì hàm số y = f(x) nghịch biến trên R. | |
BÀI TẬP
Tài liệu tham khảo
- Toán 9, Tập 1, NXB Giáo dục, 2006, trang 42.
Xem thêm
