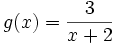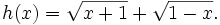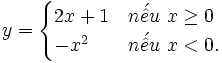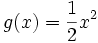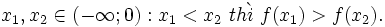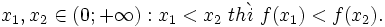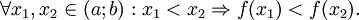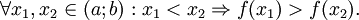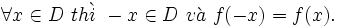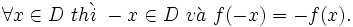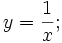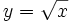Đại số 10/Chương II/§1. Hàm số
Lí thuyết[sửa]
Ôn tập về hàm số[sửa]
Hàm số. Tập xác định của hàm số[sửa]
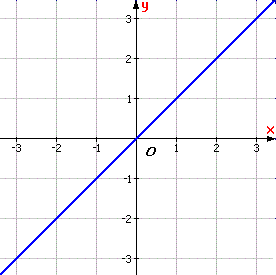
Giả sử có hai đại lượng biến thiên x và y, trong đó x nhận giá trị thuộc tập số D.
|
Nếu
với
mỗi
giá
trị
của
x
thuộc
D
có
một
và
chỉ
một
giá
trị
tương
ứng
của
y
thuộc
tập
số
thực
R
thì
ta
có
một
hàm
số.
Ta gọi x là biến số và y là hàm số của x. Tập hợp D được gọi là tập xác định của hàm số. |
|
Xét
bảng
sau:
| Năm | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2004 |
|---|---|---|---|---|---|---|---|---|---|
|
TNBQĐN (tính theo USD) |
200 | 282 | 295 | 311 | 339 | 363 | 375 | 394 | 564 |
| VÍ DỤ 1 |
Bảng
trên
đây
trích
từ
trang
Web
của
Hiệp
hội
liên
doanh
Việt
Nam
-
Thái
Lan
ngày
26
-
10
-
2005
về
thu
nhập
bình
quân
đầu
người
(TNBQĐN)
của
nước
ta
từ
năm
1995
đến
năm
2004.
Bảng này thể hiện sự phụ thuộc giữa thu nhập bình quân đầu người (kí hiệu là y) và thời gian x (tính bằng năm).
Với
mỗi
giá
trị
Vậy ta có một hàm số. Tập hợp D là tập xác định của hàm số này. Các giá trị y = 200, 282, 295,... được gọi là các giá trị của hàm số tương ứng, tại x = 1995, 1996, 1997,... |
| Hoạt động 1 |
Hãy
nêu
một
ví
dụ
thực
tế
về
hàm
số.
|
Cách cho hàm số[sửa]
Một hàm số có thể được cho bằng các cách sau:
Bằng bảng[sửa]
Hàm số trong ví dụ 1 trên, là hàm số được cho bằng bảng.
| Hoạt động 2 |
Hãy
chỉ
ra
các
giá
trị
của
hàm
số
trên
tại
x
=
2001,
2004,
1999.
|
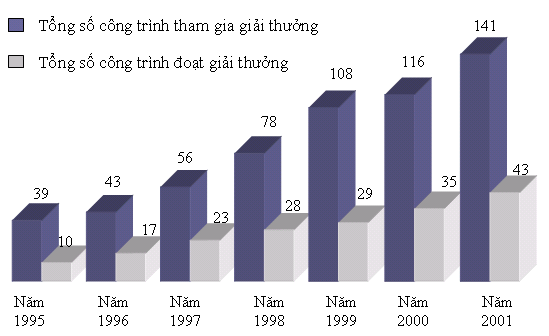
Bằng biểu đồ[sửa]
| VÍ DỤ 2 |
Biểu
đồ
dưới
(h13)
(trích
từ
báo
Khoa
học
và
Đời
sống
số
47
ngày
8
-
11
-
2002)
mô
tả
số
công
trình
khoa
học
kĩ
thuật
đăng
kí
dự
giải
thưởng
sáng
tạo
Khoa
học
Công
nghệ
Việt
Nam
và
số
công
trình
đoạt
giải
hàng
năng
từ
1995
đến
2001.
Biểu đồ này xác định hai hàm số trên cùng tập xác định
|
| Hoạt động 3 |
Hãy
chỉ
ra
các
giá
trị
của
mỗi
hàm
số
trên
tại
các
giá
trị
 .
. |
Bằng công thức[sửa]
| Hoạt động 4 |
Hãy
kể
các
hàm
số
đã
học
ở
Trung
học
cơ
sở.
|
Các
hàm
số
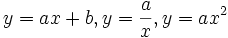 là
những
hàm
số
được
cho
bởi
công
thức.
là
những
hàm
số
được
cho
bởi
công
thức.
Khi cho hàm số bằng công thức mà không chỉ rõ tập xác định của nó thì ta quy ước như sau:
|
Tập
xác
định
của
hàm
số
y
=
f(x)
là
tập
hợp
tất
cả
các
số
thực
x
sao
cho
biểu
thức
f(x)
có
nghĩa.
|
|
| VÍ DỤ 3 |
Tìm
tập
xác
định
của
hàm
số
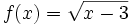 .
. |
| Lời giải |
Biểu
thức
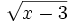 có
nghĩa
khi
x
-
3
≥
0,
tức
là
khi
x
≥
3.
Vậy
tập
xác
định
của
hàm
số
đã
cho
là
D
=
[3;+∞).
có
nghĩa
khi
x
-
3
≥
0,
tức
là
khi
x
≥
3.
Vậy
tập
xác
định
của
hàm
số
đã
cho
là
D
=
[3;+∞). |
| Hoạt động 5 |
Tìm
tập
xác
định
của
các
hàm
số
sau:
a)
b)
|
-
-
- CHÚ Ý
- Một hàm số có thể được xác định bởi hai, ba,... công thức. Chẳng hạn, cho hàm số:
-
-
-
- nghĩa là với x ≥ 0 hàm số được xác định bởi biểu thức f(x) = 2x + 1, với x < 0 hàm số được xác định bởi biểu thức g(x) = -x2.
-
| Hoạt động 6 |
Tính
giá
trị
của
hàm
số
ở
chú
ý
trên
tại
x
=
-2
và
x
=
5.
|
Đồ thị của hàm số[sửa]
|
Đồ
thị
của
hàm
số
y
=
f(x)
xác
định
trên
tập
D
là
tập
hợp
tất
cả
các
điểm
M(x;f(x))
trên
mặt
phẳng
tọa
độ
với
mọi
x
thuộc
D.
|
|
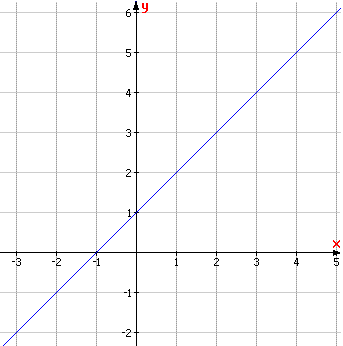
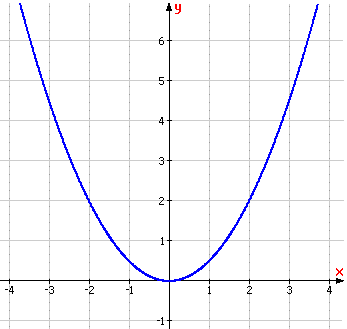
| VÍ DỤ 4 |
Trong
Sách
giáo
khoa
Toán
9,
ta
đã
biết
đồ
thị
của
hàm
số
bậc
nhất
y
=
ax
+
b
(a
≠
0)
là
một
đường
thẳng,
đồ
thị
của
hàm
số
bậc
hai
y
=
ax2
là
một
đường
parabol.
|
|
||||
| Hình 14 |
| Hoạt động 7 |
Dựa
vào
đồ
thị
của
hai
hàm
số
đã
cho
trong
hình
14
a) Tính f(-2), f(-1), f(0), f(2), g(-1), g(-2), g(0). b) Tìm x, sao cho f(x) = 2. c) Tìm x, sao cho g(x) = 2. |
Ta
thường
gặp
trường
hợp
đồ
thị
của
hàm
số
y
=
f(x)
là
một
đường
(đường
thẳng,
đường
cong,...).
Khi
đó,
ta
nói
y
=
f(x)
là
phương
trình
của
đường
đó.
Chẳng
hạn:
-
- y = ax + b là phương trình của một đường thẳng.
- y = ax2 (a ≠ 0) là phương trình của một đường parabol.
Sự biến thiên của hàm số[sửa]
Ôn tập[sửa]
|
|
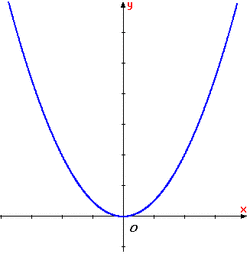
Xét
đồ
thị
hàm
số
y
=
f(x)
=
x2
(h.15a).
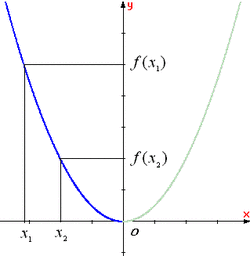
- Ta thấy trên khoảng (-∞;0) đồ thị "đi xuống" từ trái sang phải (h.15b) và với
Như vậy, khi giá trị của biến số tăng thì giá trị của hàm số giảm.
Ta nói, hàm số y = x2 nghịch biến trên khoảng (-∞;0).
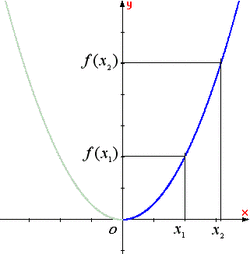
- Trên khoảng (0;+∞) đồ thị "đi lên" từ trái sang phải (h.15c) và với
Như vậy, khi giá trị của biến số tăng thì giá trị của hàm số cũng tăng.
Ta nói, hàm số y = x2 đồng biến trên khoảng (0;+∞).
Tổng
quát
|
Hàm
số
y
=
f(x)
gọi
là
đồng
biến
(tăng)
trên
khoảng
(a;b)
nếu
Hàm số y = f(x) gọi là nghịch biến (giảm) trên khoảng (a;b) nếu |
|
Bảng biến thiên[sửa]
Xét chiều biến thiên của một hàm số là tìm các khoảng đồng biến và nghịch biến của nó. Kết quả xét chiều biến thiên được tổng kết trong một bảng gọi là bảng biến thiên.
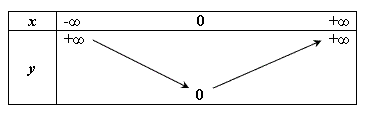
| VÍ DỤ 5 |
Hàm
số
y
=
x2
có
bảng
biến
thiên
như
sau:
Tại x = 0 thì y = 0.
|
Tính chẵn lẻ của hàm số[sửa]
Hàm số chẵn, hàm số lẻ[sửa]
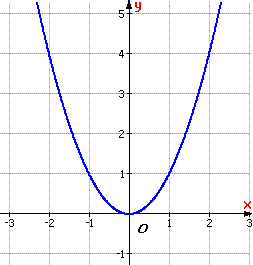
Xét đồ thị của hai hàm số y = f(x) = x2 và y = g(x) = x (h.16).
| Hình 16 | |
Đường parabol y = x2 có trục đối xứng là Oy. Tại hai giá trị đối nhau của biến số x, hàm số nhận cùng một giá trị.
-
-
- f(-1) = f(1) = 1, f(-2) = f(2) = 4,...
-
Đường thẳng y = x có tâm đối xứng là gốc tọa độ O. Tại hai giá trị đối nhau của biến số x, hàm số nhận hai giá trị đối nhau.
-
-
- g(-1) = -g(1), g(-2) = -g(2),...
-
Hàm số y = x2 là một ví dụ về hàm số chẵn.
Hàm số y = x là một ví dụ về hàm số lẻ.
Tổng
quát
|
Hàm
số
y
=
f(x)
với
tập
xác
định
D
gọi
là
hàm
số
chẵn
nếu
Hàm số y = f(x) với tập xác định D gọi là hàm số lẻ nếu |
|
| Hoạt động 8 |
Xét
tính
chẵn
lẻ
của
các
hàm
số
a) y = 3x2 - 2;
b)
c)
|
-
-
- CHÚ Ý
- Một hàm số không nhất thiết phải là hàm số chẵn hoặc hàm số lẻ. Chẳng hạn, hàm số y = 2x + 1 không là hàm số chẵn, cũng không là hàm số lẻ vì giá trị của nó tại x = 1 và x = -1 tương ứng là 3 và -1. Hai giá trị này không bằng nhau và cũng không đối nhau.
-
Đồ thị của hàm số chẵn, hàm số lẻ[sửa]
Nhận xét về đồ thị của hàm số y = x2 và y = x trong mục 1 cũng đúng cho trường hợp tổng quát. Ta có kết luận sau:
|
Đồ
thị
của
hàm
số
chẵn
nhận
trục
tung
làm
trục
đối
xứng.
Đồ thị của hàm số lẻ nhận gốc tọa độ làm tâm đối xứng. |
|
BÀI TẬP[sửa]
| 1. Tìm tập xác định của các hàm số | ||
a)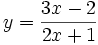 |
b)
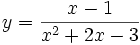
|
c)
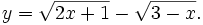
|
2. Cho hàm số
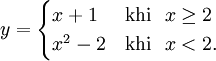
Tính giá trị của hàm số đó tại x = 3; x = -1; x = 2.
3.
Cho
hàm
số
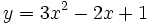 .
Các
điểm
sau
có
thuộc
đồ
thị
của
hàm
số
đó
không?
.
Các
điểm
sau
có
thuộc
đồ
thị
của
hàm
số
đó
không? |
||
| a) M(-1;6) | b) N(1;1) | c) P(0;1). |
| 4. Xét tính chẵn lẻ của các hàm số | |||
a)
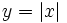
|
b)
y
=
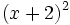
|
c)
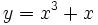
|
d)
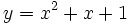
|
Tài liệu tham khảo[sửa]
- Sách in
- Đại số 10, NXB Giáo dục, 2006, Trang 32.



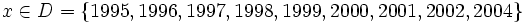 có
một
giá
trị
duy
nhất
y.
có
một
giá
trị
duy
nhất
y.