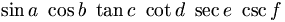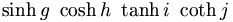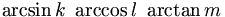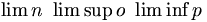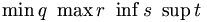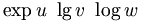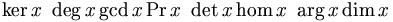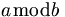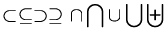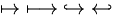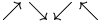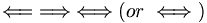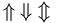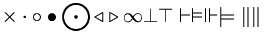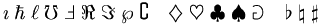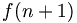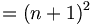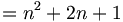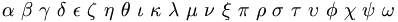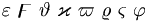Trợ giúp:Toán học
Trang này tập trung vào hướng dẫn cách viết công thức toán học phức tạp bằng mã TeX. Nếu bạn chỉ viết những công thức đơn giản, bạn có thể chỉ cần dùng mã HTML và các ký tự đặc biệt.
Mục lục
Tổng quan[sửa]
Khi bạn viết công thức toán học bằng mã TeX, bạn viết nó giữa 2 mã: <math> và </math>. Khi ấn Xem thử trước hoặc Lưu thông tin phần mềm sẽ cố hiểu công thức bạn viết; và nếu nó không sai cú pháp, phần mềm sẽ chuyển tải ra dạng hình ảnh PNG hoặc dạng mã HTML cho trình duyệt mạng đọc trong trường hợp công thức đơn giản.
Dấu
cách
và
dấu
xuống
dòng
bị
bỏ
qua.
Các
biến
số
được
tự
động
viết
nghiêng,
nhưng
chữ
số
thì
không.
Nếu
không
muốn
viết
nghiêng,
dùng
\mbox.
Ví
dụ:
<math>\mbox{abc}</math>
sẽ
cho
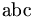 .
.
Hàm, biểu tượng, ký tự đặc biệt[sửa]
| Ý nghĩa | Mã | Thể hiện |
|---|---|---|
| Dấu thanh | \acute{a} \grave{a} \hat{a} \tilde{a} \breve{a} \check{a} \bar{a} \ddot{a} \dot{a} |
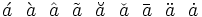 |
| Hàm (cách viết đúng) |
\sin
x
+
\ln
y
+\operatorname{sgn}
z
\sin
a
\
\cos
b
\
\tan
c
\
\cot
d
\
\sec
e
\
\csc
f |
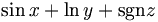
|
| Hàm (cách viết sai) | sin x + ln y + sgn z |
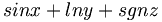 |
| Mođun |
s_k
\equiv
0
\pmod{m} a \bmod b |
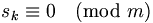
|
| Vi phân | \nabla \; \partial x \; dx \; \dot x \; \ddot y |
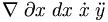 |
| Tập hợp |
\forall
\;
\exists
\;
\empty
\;
\emptyset
\;
\varnothing
\in
\ni
\not\in
\notin \subset \subseteq \supset \supseteq \cap \bigcap \cup \bigcup \biguplus |
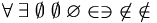
|
| \sqsubset \sqsubseteq \sqsupset \sqsupseteq \sqcap \sqcup \bigsqcup |
 |
|
| Lôgíc | p \land \wedge \; \bigwedge \; \bar{q} \to p\ lor \vee \; \bigvee \; \lnot \; \neg q \; \setminus \; \smallsetminus |
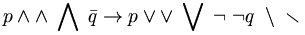 |
| Căn | \sqrt{2}\approx 1.4 |
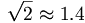 |
| \sqrt[n]{x} |
![{\sqrt[ {n}]{x}}](https://tusach.thuvienkhoahoc.com/images/math/5/e/4/5e4352778f3b156f05ef056f9793ec36.png) |
|
| Tương quan | \sim \; \approx \; \simeq \; \cong \; \le \; < \; \ge \; > \; \equiv \; \not\equiv \; \ne \; \propto \; \pm \; \mp |
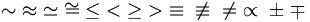 |
| Hình học | \Diamond \; \Box \; \triangle \; \angle \; \perp \; \mid \; \nmid \; \| \; 45^\circ |
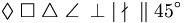 |
| Mũi tên |
\leftarrow
\;
\gets
\;
\rightarrow
\;
\to
\;
\leftrightarrow
\longleftarrow
\;
\longrightarrow |
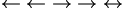
|
| \rightharpoonup \; \rightharpoondown \; \leftharpoonup \; \leftharpoondown \; \upharpoonleft \; \upharpoonright \; \downharpoonleft \; \downharpoonright |
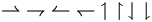 |
|
|
\Leftarrow
\;
\Rightarrow
\;
\Leftrightarrow
\Longleftarrow
\;
\Longrightarrow
\;
\Longleftrightarrow
(or
\iff) |

|
|
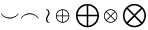
| Đặc biệt |
\eth
\;
\S
\;
\P
\;
\%
\;
\dagger
\;
\ddagger
\;
\star
\;
*
\;
\ldots
\smile
\frown
\wr
\oplus
\bigoplus
\otimes
\bigotimes |
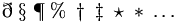
|
| Viết thường bằng \mathcal | \mathcal {45abcdenpqstuvwx} |
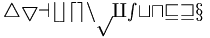 |
| Phủ định bằng \not | \not\vdots \, \not\subset \, \not\| \, \not\Rightarrow \, \not= \, \not\perp \, \not\exists \, \not < |
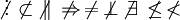 |
Số mũ, chỉ số dưới, tích phân[sửa]
| Ý nghĩa | Mã | Thể hiện | |
|---|---|---|---|
| HTML | PNG | ||
| Số mũ | a^2 |
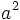 |
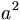 |
| Chỉ số dưới | a_2 |
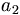 |
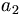 |
| Nhóm | a^{2+2} |
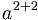 |
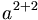 |
| a_{i,j} |
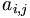 |
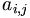 |
|
| Kết hợp hai kiểu | x_2^3 |
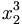 |
|
| Viết mũ và chỉ số đằng trước | {}_1^2\!X_3^4 |
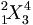 |
|
| Vi phân (cách viết đúng) | x', y'' |
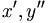 |
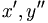 |
| Vi phân (cách viết HTML sai) | x^\prime, y^{\prime\prime} |
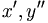 |
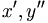 |
| Vi phân (cách viết PNG sai) | x\prime, y\prime\prime |
 |
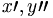 |
| Chấm vi phân | \dot{x}, \ddot{x} |
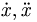 |
|
| Gạch dưới, gạch trên, véctơ | \hat a \ \bar b \ \vec c \ \overrightarrow{a b} \ \overleftarrow{c d} \ \widehat{d e f} \ \overline{g h i} \ \underline{j k l} |
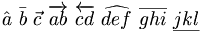 |
|
| Ngoặc ôm trên | \begin{matrix} 5050 \\ \overbrace{ 1+2+\cdots+100 } \end{matrix} |
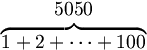 |
|
| Ngoặc ôm dưới | \begin{matrix} \underbrace{ a+b+\cdots+z } \\ 26 \end{matrix} |
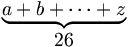 |
|
| Tổng | \sum_{k=1}^N k^2 |
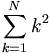 |
|
| Tích | \prod_{i=1}^N x_i |
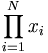 |
|
| Đồng tích | \coprod_{i=1}^N x_i |
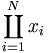 |
|
| Giới hạn | \lim_{n \to \infty}x_n |
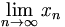 |
|
| Tích phân | \int_{-N}^{N} e^x\, dx |
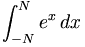 |
|
| Tích phân kép | \iint_{D}^{W} \, dx\,dy |
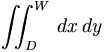 |
|
| Tích phân ba lớp | \iiint_{E}^{V} \, dx\,dy\,dz |
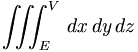 |
|
| Tích phân 4 lớp | \iiiint_{F}^{U} \, dx\,dy\,dz\,dt |
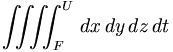 |
|
| Tích phân đường | \oint_{C} x^3\, dx + 4y^2\, dy |
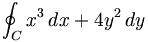 |
|
| Giao | \bigcap_1^{n} p |
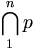 |
|
| Hợp | \bigcup_1^{k} p |
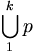 |
|
Phân số, ma trận, nhiều dòng[sửa]
| Ý nghĩa | Mã | Thể hiện | ||||
|---|---|---|---|---|---|---|
| Phân số | \frac{2}{4} or {2 \over 4} |
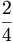 |
||||
| Liên phân số |
x
=
a_0
+
\cfrac{1}{2
+
\cfrac{1}{3
+
\cfrac{1}{5}}} (nhiều tầng, không đổi kích thước) |
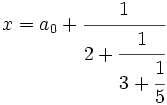 |
||||
| Hệ số nhị thức | {n \choose k} |
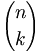 |
||||
| Phân số nhỏ | \begin{matrix} \frac{2}{4} \end{matrix} |
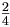 |
||||
| Ma trận | \begin{matrix} x & y \\ z & v \end{matrix} |
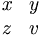 |
||||
| \begin{vmatrix} x & y \\ z & v \end{vmatrix} |
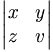 |
|||||
| \begin{Vmatrix} x & y \\ z & v \end{Vmatrix} |
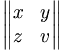 |
|||||
|
\begin{bmatrix}
0
&
\cdots
&
0
\\
\vdots
&
\ddots & \vdots \\ 0 & \cdots & 0\end{bmatrix} |
 |
|||||
| \begin{Bmatrix} x & y \\ z & v \end{Bmatrix} |
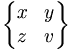 |
|||||
| \begin{pmatrix} x & y \\ z & v \end{pmatrix} |
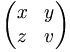 |
|||||
| Chia trường hợp | f(n) = \begin{cases} n/2, & \mbox{khi }n < 0 \\ 3n+1, & \mbox{khi }n > 0 \end{cases} |
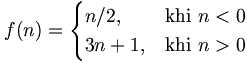 |
||||
| Phương trình nhiều dòng |
\begin{matrix}f(n+1)
&
=
&
(n+1)^2
\\
\
&
= & n^2 + 2n + 1 \end{matrix} |
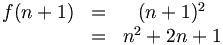 |
||||
| Phương trình nhiều dòng (dùng bảng) |
{|
|-
|<math>f(n+1)</math>
|<math>=(n+1)^2</math>
|-
|
|<math>=n^2 + 2n + 1</math>
|} |
|
Ký tự[sửa]
| Ý nghĩa | Mã | Thể hiện | |
|---|---|---|---|
| chữ Hy Lạp |
\Alpha\
\Beta\
\Gamma\
\Delta\
\Epsilon\
\Zeta\
\Eta\
\Theta\
\Iota\
\Kappa\
\Lambda\
\Mu\
\Nu\
\Xi\
\Pi\
\Rho\
\Sigma\
\Tau\
\Upsilon\
\Phi\
\Chi\
\Psi\
\Omega
\alpha\
\beta\
\gamma\
\delta\
\epsilon\
\zeta\
\eta\
\theta\
\iota\
\kappa\
\lambda\
\mu\
\nu\
\xi\
\pi\
\rho\
\sigma\
\tau\
\upsilon\
\phi\
\chi\
\psi\
\omega |
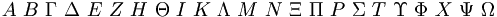
|
|
| Viết đậm kép | \mathbb{N}\ \mathbb{Z}\ \mathbb{Q}\ \mathbb{R}\ \mathbb{C} |
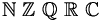 |
|
| Viết đậm véctơ | \mathbf{x}\cdot\mathbf{y} = 0 |
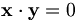 |
|
| Viết đậm chữ Hy Lạp | \boldsymbol{\alpha} + \boldsymbol{\beta} + \boldsymbol{\gamma} |
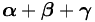 |
|
| Nghiêng | \mathit{ABCDE abcde 1234} |
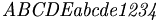 |
|
| Kiểu La Mã | \mathrm{ABCDE abcde 1234} |
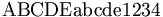 |
|
| Kiểu Fraktur | \mathfrak{ABCDE abcde 1234} |
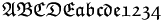 |
|
| Viết văn hoa | \mathcal{ABCDE abcde 1234} |
 |
|
| Chữ Do thái | \aleph \beth \gimel \daleth |
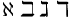 |
|
| Không bị nghiêng | \mbox{abc} |
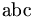 |
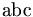 |
| Trộn kiểu nghiêng (không hay) | \mbox{if} n \mbox{is even} |
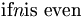 |
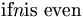 |
| Trộn kiểu nghiêng (tốt) | \mbox{if }n\mbox{ is even} |
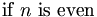 |
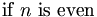 |
Ngoặc lớn, ngoặc vuông, trị[sửa]
| Ý nghĩa | Mã | Thể hiện |
|---|---|---|
| Không đẹp | ( \frac{1}{2} ) |
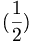 |
| Đẹp | \left ( \frac{1}{2} \right ) |
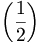 |
Có
thể
dùng
\left
và
\right
cho
từng
ngoặc
riêng
rẽ:
| Ý nghĩa | Mã | Thể hiện | |
|---|---|---|---|
| Ngoặc | \left ( \frac{a}{b} \right ) |
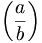 |
|
| Ngoặc vuông | \left [ \frac{a}{b} \right ] \quad \left \lbrack \frac{a}{b} \right \rbrack |
![\left[{\frac {a}{b}}\right]\quad \left\lbrack {\frac {a}{b}}\right\rbrack](https://tusach.thuvienkhoahoc.com/images/math/7/c/b/7cb5a74153ec87cdda6b92669ba685e1.png) |
|
| Ngoặc móc | \left \{ \frac{a}{b} \right \} \quad \left \lbrace \frac{a}{b} \right \rbrace |
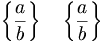 |
|
| Ngoặc nhọn | \left \langle \frac{a}{b} \right \rangle |
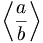 |
|
| Trị và Trị kép | \frac{a}{b} \right \vert \left \Vert \frac{c}{d} \right \| |
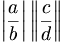 |
|
| Hàm trị nguyên | \left \lfloor \frac{a}{b} \right \rfloor \left \lceil \frac{c}{d} \right \rceil |
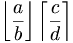 |
|
| Ngoặc chéo | \left / \frac{a}{b} \right \backslash |
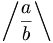 |
|
| Mũi tên lên xuống | \left \uparrow \frac{a}{b} \right \downarrow \quad \left \Uparrow \frac{a}{b} \right \Downarrow \quad \left \updownarrow \frac{a}{b} \right \Updownarrow |
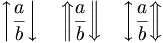 |
|
| Trộn lẫn (đủ bộ hai bên) | \left [ 0,1 \right )<br/>\left \langle \psi \right | |
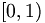 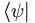
|
|
| Dùng \left. và \right. khi không muốn có ngoặc | \left . \frac{A}{B} \right \} \to X |
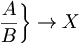 |
|
| Kích thước | \big( \Big( \bigg( \Bigg( ... \Bigg] \bigg] \Big] \big] |
![{\big (}{\Big (}{\bigg (}{\Bigg (}...{\Bigg ]}{\bigg ]}{\Big ]}{\big ]}](https://tusach.thuvienkhoahoc.com/images/math/0/a/2/0a2c41697f07213ddaa59a92738e8bd6.png) |
|
| \big\{ \Big\{ \bigg\{ \Bigg\{ ... \Bigg\rangle \bigg\rangle \Big\rangle \big\rangle |
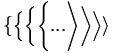 |
||
| \Big\| \bigg\| \Bigg\| ... \Bigg| \bigg| \Big| \big| |
 |
||
| \big\lfloor \Big\lfloor \bigg\lfloor \Bigg\lfloor ... \Bigg\rceil \bigg\rceil \Big\rceil \big\rceil |
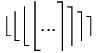 |
||
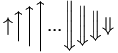
| \big\uparrow \Big\uparrow \bigg\uparrow \Bigg\uparrow ... \Bigg\Downarrow \bigg\Downarrow \Big\Downarrow \big\Downarrow |
 |
||
Dấu cách[sửa]
| Ý nghĩa | Mã | Thể hiện |
|---|---|---|
| Cách kép | a \qquad b |
 |
| Cách đơn | a \quad b |
 |
| Cách ký tự | a\ b |
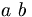 |
| Cách ký tự, không chuyển sang PNG | a \mbox{ } b |
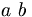 |
| Cách dài | a\;b |
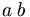 |
| Cách vừa | a\>b | [không hỗ trợ] |
| Cách ngắn | a\,b |
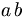 |
| Không cách | ab |
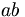 |
| Cách âm | a\!b |
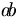 |
Gióng hàng với chữ[sửa]
Nói
chung
công
thức
như
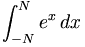 nằm
giữa
dòng
chữ
sẽ
được
thể
hiện
tương
đối
tốt,
nhờ
cài
đặt
mặc
định
của
phần
mềm.
nằm
giữa
dòng
chữ
sẽ
được
thể
hiện
tương
đối
tốt,
nhờ
cài
đặt
mặc
định
của
phần
mềm.
Nếu
muốn
chỉnh
lại,
dùng
<font
style="vertical-align:-100%;"><math>...</math></font>
và
thay
đổi
giá
trị
của
biến
vertical-align
cho
đến
khi
vừa
ý;
tuy
nhiên,
kết
quả
thể
hiện
có
thể
thay
đổi
tùy
trình
duyệt
mạng.
Bắt thể hiện bằng hình PNG[sửa]
Để
bắt
phần
mềm
thể
hiện
công
thức
bằng
hình
PNG,
thay
vì
HTML
cho
trường
hợp
đơn
giản,
thêm
\,
vào
cuối
công
thức
hoặc
\,\!
vào
bất
cứ
chỗ
nào
của
công
thức.
Ví
dụ:
| Mã | Thể hiện |
|---|---|
| a^{c+2} |
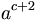 |
| a^{c+2} \, |
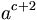 |
| a^{\,\!c+2} |
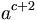 |
| a^{b^{c+2}} |
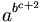 (Sai
nếu
lựa
chọn
cá
nhân
"Viết
công
thức
toán
học
bằng
HTML
nếu
có
thể"!)
(Sai
nếu
lựa
chọn
cá
nhân
"Viết
công
thức
toán
học
bằng
HTML
nếu
có
thể"!) |
| a^{b^{c+2}} \, |
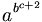 (Sai
nếu
lựa
chọn
cá
nhân
"Viết
công
thức
toán
học
bằng
HTML
nếu
có
thể"!)
(Sai
nếu
lựa
chọn
cá
nhân
"Viết
công
thức
toán
học
bằng
HTML
nếu
có
thể"!) |
| a^{b^{c+2}}\approx 5 |
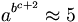 (không
cần
"\,\!")
(không
cần
"\,\!") |
| a^{b^{\,\!c+2}} |
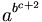 |
| \int_{-N}^{N} e^x\, dx |
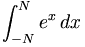 |
| \int_{-N}^{N} e^x\, dx \, |
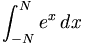 |
| \int_{-N}^{N} e^x\, dx \,\! |
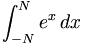 |
Có thể thêm chú thích để người khác đừng thay đổi:
- <!-- Đoạn \,\! để tạo hình PNG cho công thức, thay vì HTML. Xin đừng xóa nó.-->
Ví dụ[sửa]
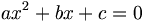
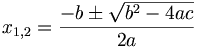
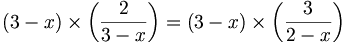
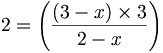
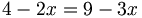
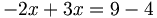
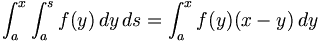
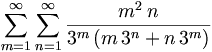
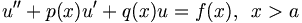
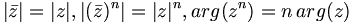
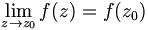
![\phi _{n}(\kappa )={\frac {1}{4\pi ^{2}\kappa ^{2}}}\int _{0}^{\infty }{\frac {\sin(\kappa R)}{\kappa R}}{\frac {\partial }{\partial R}}\left[R^{2}{\frac {\partial D_{n}(R)}{\partial R}}\right]\,dR\,](https://tusach.thuvienkhoahoc.com/images/math/a/f/a/afa9993f0c461142dd2c9593d418c829.png)
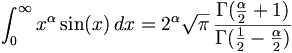
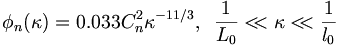
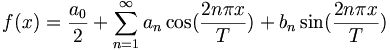
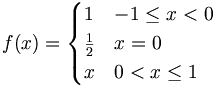
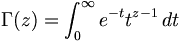
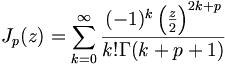
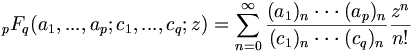
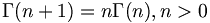
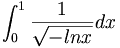
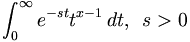
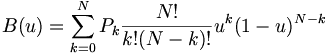
![u(x,y)={\frac {1}{{\sqrt {2\pi }}}}\int _{0}^{\infty }f(\xi )\left[g(|x+\xi |,y)+g(|x-\xi |,y)\right]\,d\xi \,](https://tusach.thuvienkhoahoc.com/images/math/d/4/4/d44dc4d14473bffd971b327bd3bb408c.png)
Trình soạn thảo công thức toán[sửa]
-
Trên
thanh
công
cụ
soạn
thảo,
click
vào
biểu
tượng
 .
. - Lựa chọn các kí tự thích hợp để soạn thảo công thức.