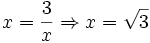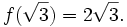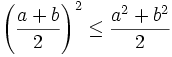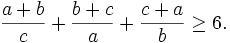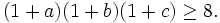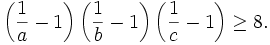Đại số 10/Chương IV/§1. Bất đẳng thức
Mục lục
Lí thuyết[sửa]
Ôn tập bất đẳng thức[sửa]
Bất đẳng thức là gì?[sửa]
| Hoạt động 1 |
Trong
các
mệnh
đề
sau,
mệnh
đề
nào
đúng?
a)
3,25
<
4
b)
|
| Hoạt động 2 |
Chọn
dấu
thích
hợp
(<,
=,
>)
để
khi
điền
vào
ô
vuông
ta
được
một
mệnh
đề
đúng.
a)
|
|
Các
mệnh
đề
dạng
"a
<
b",
"a
>
b",
"a
≤
b"
và
"a
≥
b"
được
gọi
là
bất
đẳng
thức.
Trong
đó
các
kí
hiệu
a
và
b
có
thể
là
các
biểu
thức
của
các
biến.
|
|
Các
bất
đẳng
thức
dạng:
"a
<
b"
và
"a
>
b"
được
gọi
là
các
bất
đẳng
thức
nghiêm
ngặt,
còn
các
bất
đẳng
thức
dạng:
"a
≤
b"
và
"a
≥
b"
được
gọi
là
bất
đẳng
thức
không
nghiêm
ngặt.
Một bất đẳng thức có thể đúng, có thể sai. Việc chứng minh một bất đẳng thức nào đó là đúng với các giá trị của các biến thuộc một tập hợp cho trước được gọi là bài toán chứng minh bất đẳng thức.
Bất đẳng thức hệ quả và bất đẳng thức tương đương[sửa]
Ta nói: bất đẳng thức a < c là hệ quả của bất đẳng thức a < b và b < c. Vì:
- Nếu a < b và b < c thì a < c (tính chất bắc cầu).
Ta nói: bất đẳng thức a + c < b + c là hệ quả của bất đẳng thức a < b với c tùy ý. Vì:
- Nếu a < b thì a + c < b + c với c tùy ý (tính chất cộng của hai vế bất đẳng thức với một số).
Tổng
quát,
ta
có
định
nghĩa
|
Nếu
mệnh
đề
"a
<
b
 c
<
d"
đúng
thì
ta
nói
bất
đẳng
thức
c
<
d
là
bất
đẳng
thức
hệ
quả
của
bất
đẳng
thức
a
<
b.
c
<
d"
đúng
thì
ta
nói
bất
đẳng
thức
c
<
d
là
bất
đẳng
thức
hệ
quả
của
bất
đẳng
thức
a
<
b.
 c
<
d.
c
<
d. |
|
| Hoạt động 3 |
Chứng
minh
rằng:
a
<
b
 a
-
b
<
0(*).
a
-
b
<
0(*). |
Từ đó suy ra, để chứng minh bất đẳng thức a < b ta chỉ cần chứng minh hiệu a - b < 0.
| VÍ DỤ 1 |
Chứng
minh
rằng:
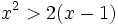 với
mọi
x.
với
mọi
x. |
| Lời giải |
Xét
dấu
của
hiệu
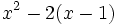 .
Ta
có:
.
Ta
có:
Vậy,
|
Một
cách
khác,
khi
so
sánh
hai
số,
hai
biểu
thức
hoặc
chứng
minh
một
bất
đẳng
thức,
ta
có
thể
sử
dụng
các
tính
chất
sau
của
các
bất
đẳng
thức
nghiêm
ngặt.
Các
tính
chất
này
cũng
đúng
cho
các
bất
đẳng
thức
không
nghiêm
ngặt.
Tính chất của bất đẳng thức[sửa]
Để thuận tiện, ta quy ước cách gọi:
- Hai bất đẳng thức dạng a > b và c > d được gọi là cùng chiều (với nhau).
- Hai bất đẳng thức dạng a > b và c < d được gọi là ngược chiều (với nhau).
| TT | Tính chất | Điều kiện | Phát biểu |
|---|---|---|---|
| 1. |
a
<
b
 a
+
c
<
b
+
c
a
+
c
<
b
+
c |
với c tùy ý | Cộng hai vế của bất đẳng với một số ta được một bất đẳng thức cùng chiều và tương đương với bất đẳng thức đã cho. |
| 2. |
a
<
b
 ac
<
bc
ac
<
bc |
với c > 0 | Nhân hai vế của bất đẳng với một số dương ta được một bất đẳng thức cùng chiều và tương đương với bất đẳng thức đã cho. |
| 3. |
a
<
b
 ac
>
bc
ac
>
bc |
với c < 0 | Nhân hai vế của bất đẳng với một số âm ta được một bất đẳng thức ngược chiều và tương đương với bất đẳng thức đã cho. |
| 4. |
a
<
b
và
c
<
d
 a
+
c
<
b
+
d
a
+
c
<
b
+
d |
Cộng hai bất đẳng thức cùng chiều ta được một bất đẳng thức cùng chiều. | |
| 5. |
a
<
b
và
c
<
d
 a.c
<
b.d
a.c
<
b.d |
với a > 0, c > 0 | Nhân hai bất đẳng thức cùng chiều có tất cả các vế đều dương, ta được một bất đẳng thức cùng chiều. |
| 6. |
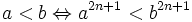 |
với n nguyên dương | Nâng hai vế của bất đẳng thức lên một lũy thừa lẻ, nguyên dương ta được một bất đẳng thức cùng chiều và tương đương với bất đẳng thức đã cho. |
| 7. |
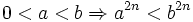 |
với n nguyên dương | Nâng hai vế của bất đẳng thức lên một lũy thừa chẵn, nguyên dương ta được một bất đẳng thức cùng chiều. |
| 8. |
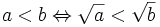 |
với a > 0 | Lấy căn bậc hai hai vế của một bất đẳng thức ta được một bất đẳng thức cùng chiều và tương đương với bất đẳng thức đã cho. |
| 9. |
![a<b\Leftrightarrow {\sqrt[ {3}]{a}}<{\sqrt[ {3}]{b}}](https://tusach.thuvienkhoahoc.com/images/math/5/3/d/53d2da3d1d118ffa114ffa8a34012c5e.png) |
Lấy căn bậc ba hai vế của một bất đẳng thức ta được một bất đẳng thức cùng chiều và tương đương với bất đẳng thức đã cho. |
| VÍ DỤ 2 |
Không
dùng
bảng
số
hoặc
máy
tính,
hãy
so
sánh
hai
số
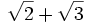 và
3.
và
3. |
| Lời giải |
Cách
1:
Giả
sử
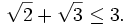 Do
hai
vế
của
bất
đẳng
thức
đều
dương
nên
bình
phương
hai
vế
ta
được:
Do
hai
vế
của
bất
đẳng
thức
đều
dương
nên
bình
phương
hai
vế
ta
được:
Vậy
Dễ
thấy
|
Bất đẳng thức chứa dấu giá trị tuyệt đối[sửa]
| Hoạt động 4 |
Nhắc
lại
định
nghĩa
giá
trị
tuyệt
đối
và
tính
giá
trị
tuyệt
đối
của
các
số
sau:
a)
0
b)
1,25
c)
|
Từ
định
nghĩa
giá
trị
tuyệt
đối,
ta
suy
ra
các
tính
chất
sau:
|
| VÍ DỤ 3 |
Cho
![x\in [-2;0].](https://tusach.thuvienkhoahoc.com/images/math/e/1/8/e18d0eea6da9fdcf44433118fb335306.png) Chứng
minh
rằng
Chứng
minh
rằng
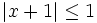 .
. |
| Lời giải |
Ta
có:
|
| VÍ DỤ 4 |
Tìm
tập
xác
định
của
hàm
số
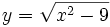 .
. |
| Lời giải |
Hàm
số
xác
định
khi
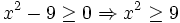 (tính
chất
(*))
(tính
chất
(*))
Vậy
|
Bất đẳng thức giữa trung bình cộng và trung bình nhân[sửa]
Bất đẳng thức giữa trung bình cộng và trung bình nhân hay còn được gọi là bất đẳng thức Cô-si (Cauchy).
Bất đẳng thức Cô-si[sửa]
- Định lí
|
Trung
bình
nhân
của
hai
số
không
âm
nhỏ
hơn
hoặc
bằng
trung
bình
cộng
của
chúng.
Trung
bình
nhân
của
hai
số
không
âm
bằng
trung
bình
cộng
của
chúng
khi
và
chỉ
khi
hai
số
đó
bằng
nhau.
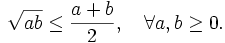 (1)
(1)
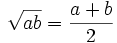 xảy
ra
khi
và
chỉ
khi
a
=
b.
xảy
ra
khi
và
chỉ
khi
a
=
b. |
|
CHỨNG
MINH
Xét
dấu
của
hiệu:
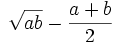 .
Ta
có:
.
Ta
có:
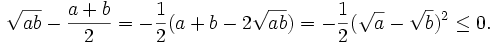
Vậy
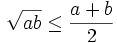 .
.
Đẳng
thức
xảy
ra
khi
và
chỉ
khi
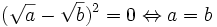 .
.
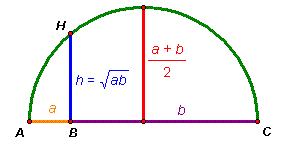
CHÚ Ý: Có thể chứng minh bất đẳng thức Cô-si bằng hình học như sau:
Xét nửa đường tròn đường kính AC = a + b. Các đoạn thẳng AB, BC, BH có độ dài lần lượt là a, b, h (hình vẽ).
Khi
đó,
ta
có
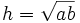 và
rõ
ràng
h
=
BH
không
thể
vượt
quá
bán
kính
của
nửa
đường
tròn,
tức
là:
và
rõ
ràng
h
=
BH
không
thể
vượt
quá
bán
kính
của
nửa
đường
tròn,
tức
là:
Đẳng thức chỉ có thể xảy ra khi B là tâm của đường tròn, tức là khi a = b.
| VÍ DỤ 5 |
Cho
a
>
0,
b
>
0.
Chứng
minh
rằng:
|
| Lời giải |
a)
Vì
a
>
0,
b
>
0
nên
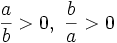 .
Áp
dụng
bất
đẳng
thức
Cô-si
cho
hai
số
.
Áp
dụng
bất
đẳng
thức
Cô-si
cho
hai
số
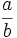 và
và
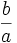 ,
ta
có:
,
ta
có:
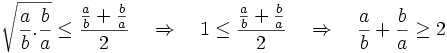 (đpcm)
(đpcm)
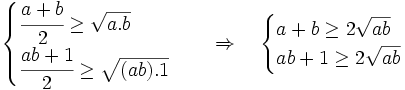
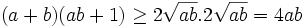 (đpcm)
(đpcm)
|
Từ
bất
đẳng
thức
Cô-si
ta
suy
ra
ba
hệ
quả
sau:
Các hệ quả[sửa]
Hệ quả 1[sửa]
Tổng
của
một
số
dương
với
nghịch
đảo
của
nó
luôn
lớn
hơn
hoặc
bằng
2.
Tức
là:
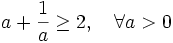 . . |
Hệ quả 2[sửa]
| Nếu x, y cùng dương và có tổng không đổi thì tích xy lớn nhất khi và chỉ khi x = y. |
CHỨNG
MINH
Đặt S = x + y và áp dụng bất đẳng thức Cô-si cho hai số x và y ta có:
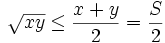 ,
do
đó
,
do
đó
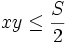 .
.
Đẳng
thức
xảy
ra
khi
và
chỉ
khi
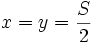 .
.
Ý
NGHĨA
HÌNH
HỌC
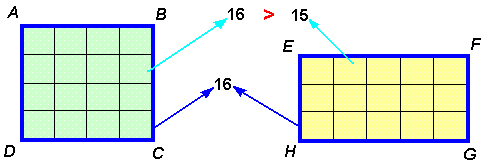
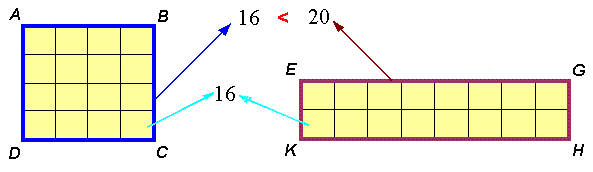
- Trong tất cả các hình chữ nhật có cùng chu vi, hình vuông có diện tích lớn nhất (hình 26).
Hệ quả 3[sửa]
| Nếu x, y cùng dương và có tích không đổi thì tổng x + y nhỏ nhất khi và chỉ khi x = y. |
CHỨNG
MINH
Cách chứng minh tương tự như cách chứng minh hệ quả 2 ở trên.
Ý
NGHĨA
HÌNH
HỌC
- Trong tất cả các hình chữ nhật có cùng diện tích, hình vuông có chu vi nhỏ nhất (hình 27).
| VÍ DỤ 6 |
Tìm
giá
trị
nhỏ
nhất
của
hàm
số
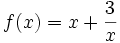 với
x
>
0.
với
x
>
0. |
| Lời giải |
Cách
1:
Do
x
>
0
nên
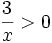 .
Áp
dụng
bất
đẳng
thức
Cô-si
cho
hai
số
x
và
.
Áp
dụng
bất
đẳng
thức
Cô-si
cho
hai
số
x
và
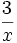 .
Ta
có:
.
Ta
có:
Vậy
giá
trị
nhỏ
nhất
của
hàm
số
tổng
Vậy
hàm
số
trên
đạt
giá
trị
nhỏ
nhất
bằng:
|
BÀI TẬP[sửa]
1. Không dùng bảng hoặc máy tính hãy so sánh các số sau:
-
-
-
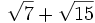 và
và
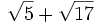
-
-
2.
Bằng
cách
xét
hiệu
hoặc
biến
đổi
tương
đương,
hãy
chứng
minh
các
bất
đẳng
thức
sau:
a) Với a, b bất kì, chứng minh rằng:
b)
Với
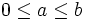 ,
chứng
minh
rằng:
,
chứng
minh
rằng:
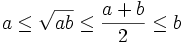
c)
Cho
a,
b,
c
là
độ
dài
ba
cạnh
của
một
tam
giác.
Chứng
minh
rằng:
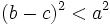
d)
Chứng
minh
rằng:
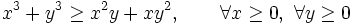
3.
Áp
dụng
các
tính
chất
của
bất
đẳng
thức
có
chứa
giá
trị
tuyệt
đối.
Hãy:
a)
Chứng
minh
rằng:
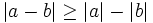
b)
Chứng
minh
rằng:
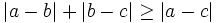
c)
Tìm
tập
xác
định
của
hàm
số:
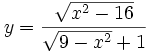
4.
Áp
dụng
bất
đẳng
thức
Cô-si.
a) Cho ba số a, b, c dương. Chứng minh rằng:
b) Cho ba số dương a, b và c thỏa mãn abc = 1. Chứng minh rằng:
c)
Cho
ba
số
dương
a,
b
và
c
thỏa
mãn
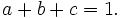 Chứng
minh
rằng:
Chứng
minh
rằng:
d)
Để
chứng
minh
bất
đẳng
thức:
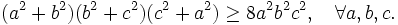
Một học sinh đã giải như sau:
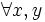 ta
có:
ta
có:
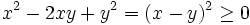
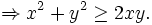 Do
đó:
Do
đó:
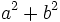 |
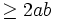 |
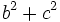 |
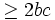 |
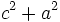 |
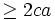 |
| ______________________________________________________ | |
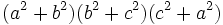 |
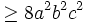 (đpcm)
(đpcm) |
Sai
lầm
ở
đâu?
Hãy
giải
lại
cho
đúng!
5.
Tìm
giá
trị
lớn
nhất,
giá
trị
nhỏ
nhất
của
các
hàm
số:
a)
Tìm
giá
trị
lớn
nhất
của
hàm
số
sau:
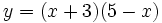 với
với
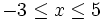 .
.
b) Tìm giá trị nhỏ nhất của các hàm số sau:
-
-
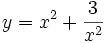 với
x
≠
0.
với
x
≠
0.
-
-
-
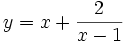 với
x
>
1.
với
x
>
1.
-
Xem thêm[sửa]
- Đại số 8/Chương IV/§1. Liên hệ giữa thứ tự và phép cộng
- Đại số 8/Chương IV/§2. Liên hệ giữa thứ tự và phép nhân
Liên kết ngoài[sửa]
- Bất đẳng thức trên Wikipedia:



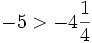 c)
c)
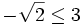
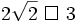 b)
b)
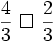 c)
c)
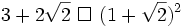 d)
d)
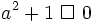 với
a
là
một
số
đã
cho.
với
a
là
một
số
đã
cho.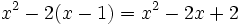
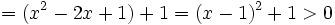 (dễ
thấy)
(dễ
thấy)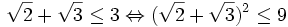 (tính
chất
7)
(tính
chất
7)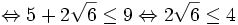 (tính
chất
1)
(tính
chất
1)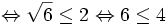 vô
lí.
(tính
chất:
2
và
7)
vô
lí.
(tính
chất:
2
và
7)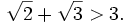
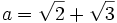 và
b
=
3.
Ta
có:
và
b
=
3.
Ta
có: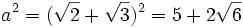
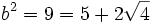
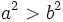 ,
nên
theo
tính
chất
8
ta
có:
a
>
b.
,
nên
theo
tính
chất
8
ta
có:
a
>
b.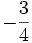 d)
d)
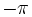
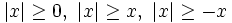
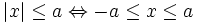 với
a
>
0
(Bất
đẳng
thức
kép)
với
a
>
0
(Bất
đẳng
thức
kép)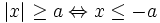 hoặc
hoặc
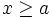 với
a
>
0
(Bất
đẳng
thức
kép)
với
a
>
0
(Bất
đẳng
thức
kép)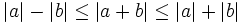 (Bất
đẳng
thức
kép,
Bất
đẳng
thức
tam
giác)
(Bất
đẳng
thức
kép,
Bất
đẳng
thức
tam
giác)![x\in [-2;0]\Rightarrow -2\leq x\leq 0](https://tusach.thuvienkhoahoc.com/images/math/d/0/a/d0a40bfe276fae6410517746ce6cbdfd.png)
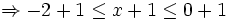
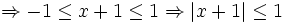 (đpcm).
(tính
chất
2)
(đpcm).
(tính
chất
2)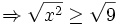 (tính
chất
8)
(tính
chất
8)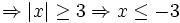 hoặc
hoặc
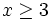 .
(tính
chất
3)
.
(tính
chất
3)![D=(-\infty ;-3]\cup [3;+\infty )](https://tusach.thuvienkhoahoc.com/images/math/6/9/0/6909a6aa563126f8d8ce0ec89be655f8.png)
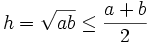

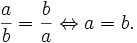
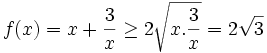 và
và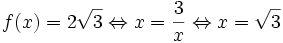 .
.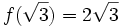 .
.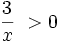 và
tích
của
chúng:
và
tích
của
chúng:
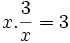 -không
đổi.
Nên
theo
hệ
quả
3,
ta
có:
-không
đổi.
Nên
theo
hệ
quả
3,
ta
có: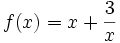 nhỏ
nhất
khi
và
chỉ
khi
nhỏ
nhất
khi
và
chỉ
khi