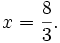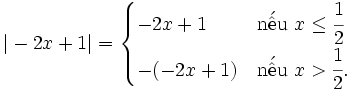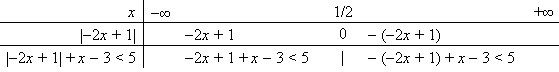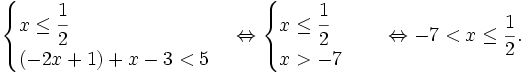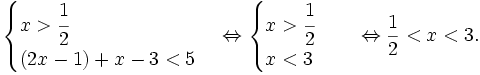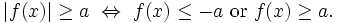Đại số 10/Chương IV/§3. Dấu của nhị thức bậc nhất
Lí thuyết[sửa]
Nhị thức bậc nhất và dấu của nó[sửa]
Nhiều bài toán dẫn đến việc xét xem một biểu thức f(x) đã cho nhận giá trị âm (hoặc dương) với những giá trị nào của x. Ta gọi việc làm đó là xét dấu của biểu thức f(x). Dưới đây, ta sẽ tìm hiểu về nhị thức bậc nhất và dấu của nó.
Nhị thức bậc nhất[sửa]
|
Nhị
thức
bậc
nhất
đối
với
x
là
biểu
thức
dạng
ax
+
b,
trong
đó
a
và
b
là
hai
số
cho
trước,
với
a
≠
0
và
a
được
gọi
là
hệ
số
của
x
hay
hệ
số
của
nhị
thức.
|
|
Ta
đã
biết,
phương
trình
ax
+
b
=
0
(a
≠
0)
có
một
nghiệm
duy
nhất
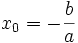 .
Nghiệm
đó
cũng
được
gọi
là
nghiệm
của
nhị
thức
bậc
nhất
f(x)
=
ax
+
b.
Nó
có
vai
trò
rất
quan
trọng
trong
việc
xét
dấu
của
nhị
thức
bậc
nhất
f(x).
.
Nghiệm
đó
cũng
được
gọi
là
nghiệm
của
nhị
thức
bậc
nhất
f(x)
=
ax
+
b.
Nó
có
vai
trò
rất
quan
trọng
trong
việc
xét
dấu
của
nhị
thức
bậc
nhất
f(x).
| Hoạt động 1 |
Cho
bất
phương
trình:
-2x
+
3
>
0.
a) Giải bất phương trình và biểu diễn trên trục số tập nghiệm của nó. b) Từ đó hãy điền các cụm từ "cùng dấu" hoặc "trái dấu" vào các chỗ trống:
c) Việc điền vào chỗ trống trong câu b) sẽ thay đổi như thế nào nếu f(x) = 2x - 3? |
Từ
kết
quả
của
câu
b)
và
c)
ta
có
định
lí
sau
đây.
Dấu của nhị thức bậc nhất[sửa]
ĐỊNH LÍ
|
Nhị
thức
bậc
nhất
f(x)
=
ax
+
b
cùng
dấu
với
hệ
số
a
khi
x
lớn
hơn
nghiệm
và
trái
dấu
với
hệ
số
a
khi
x
nhỏ
hơn
nghiệm
của
nó.
|
|
CHỨNG
MINH
Đặt
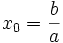 ,
ta
viết
nhị
thức
bậc
nhất
f(x)
=
ax
+
b
như
sau:
,
ta
viết
nhị
thức
bậc
nhất
f(x)
=
ax
+
b
như
sau:
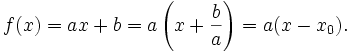
Khi
x
>
x0
thì
x
-
x0
>
0
nên
dấu
của
a(x
-
x0)
trùng
với
dấu
của
a.
Khi x < x0 thì x - x0 > 0 nên dấu của a(x - x0) trái với dấu của a.
Kết
quả
của
định
lí
trên
được
tóm
tắt
trong
bảng
sau:
Ta gọi bảng này là bảng xét dấu nhị thức f(x) = ax + b.
| VÍ DỤ 1 |
Xét
dấu
nhị
thức:
a) f(x) = 2x - 3; b) f(x) = 2 - 3x. |
| Lời giải | |
| Hoạt động 2 |
Xét
dấu
các
nhị
thức
f(x)
=
3x
+
2;
g(x)
=
-2x
+
5.
|
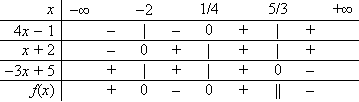
Xét dấu tích, thương các nhị thức bậc nhất[sửa]
- Giả sử f(x) là một tích của những nhị thức bậc nhất. Áp dụng định lí về dấu của nhị thức bậc nhất có thể xét dấu từng nhân tử. Từ đó lập bảng xét dấu chung cho tất cả các nhị thức bậc nhất có mặt trong f(x) ta suy ra được dấu của f(x). Trường hợp f(x) là một thương của những nhị thức bậc nhất cũng được xét tương tự.
| VÍ DỤ 2 |
Xét
dấu
biểu
thức:
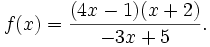
|
| Lời giải | |
| Hoạt động 3 |
Xét
dấu
biểu
thức
f(x)
=
(2x
-
1).(-x
+
3).
|
Áp dụng[sửa]
Giải bất phương trình f(x) > 0 thực chất là xét xem biểu thức f(x) nhận giá trị dương với những giá trị nào của x (do đó cũng biết f(x) nhận giá trị âm với những giá trị nào của x), làm như vậy ta nói đã xét dấu biểu thức f(x).
Giải bất phương trình tích, bất phương trình chứa ẩn ở mẫu thức[sửa]
| VÍ DỤ 3 |
Giải
bất
phương
trình:
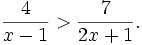 |
| Lời giải |
Vì
không
biết
dấu
của
các
biểu
thức
x
-
1
và
2x
+
1,
nên
ta
không
được
phép
nhân
cả
hai
vế
của
bất
phương
trình
với
biểu
thức
(x
-
1).(2x
+
1)
để
khử
mẫu
số.
Ta cần tiến hành như sau: chuyển vế phải sang vế trái, bất phương trình đã cho tương đương với:
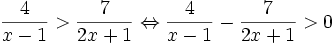
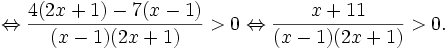 (*)
(*)
Từ bảng xét dấu trên ta suy ra tập nghiệm của bất phương trình (*) là: 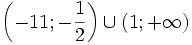 |
| Hoạt động 4 |
Giải
bất
phương
trình
x3
-
4x
<
0.
|
Giải phương trình/bất phương trình chứa ẩn trong dấu giá trị tuyệt đối[sửa]
Ta
đã
biết,
hai
phương
pháp
để
khử
dấu
giá
trị
tuyệt
đối
cho
các
phương
trình
dạng
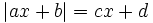 và
và
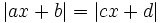 .
Ngoài
ra,
để
giải
các
phương
trình
(bất
phương
trình)
chứa
ẩn
trong
dấu
giá
trị
tuyệt
đối,
ta
có
thể
khử
dấu
giá
trị
tuyệt
đối
bằng
cách
xét
dấu
nhị
thức
ax
+
b.
Cụ
thể
là,
chia
tập
xác
định
của
phương
trình
(bất
phương
trình)
thành
nhiều
khoảng
(nửa
khoảng,
đoạn)
khác
nhau,
trên
các
khoảng
(nửa
khoảng,
đoạn)
đó
ta
giải
các
phương
trình
không
chứa
giá
trị
tuyệt
đối.
.
Ngoài
ra,
để
giải
các
phương
trình
(bất
phương
trình)
chứa
ẩn
trong
dấu
giá
trị
tuyệt
đối,
ta
có
thể
khử
dấu
giá
trị
tuyệt
đối
bằng
cách
xét
dấu
nhị
thức
ax
+
b.
Cụ
thể
là,
chia
tập
xác
định
của
phương
trình
(bất
phương
trình)
thành
nhiều
khoảng
(nửa
khoảng,
đoạn)
khác
nhau,
trên
các
khoảng
(nửa
khoảng,
đoạn)
đó
ta
giải
các
phương
trình
không
chứa
giá
trị
tuyệt
đối.
| VÍ DỤ 4 |
Giải
phương
trình:
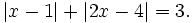 (1) (1) |
| Lời giải |
Theo
định
nghĩa
giá
trị
tuyệt
đối
ta
có:
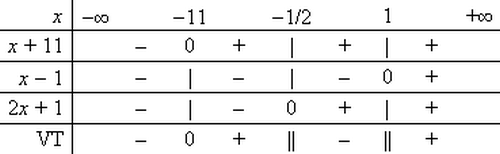
Lập
bảng
khử
dấu
giá
trị
tuyệt
đối
chung
cho:
Trên
khoảng
(-∞;
1),
ta
có:
(1)
Trên
nửa
khoảng
[1;2),
ta
có:
(1)
Trên
nửa
khoảng
[2;
+∞),
ta
có:
(1)
Vậy
phương
trình
(1)
có
hai
nghiệm
là:
|
CHÚ Ý: Khi giải phương trình chứa ẩn trong dấu giá trị tuyệt đối bằng phương pháp lập bảng như trên, ta cần lưu ý rằng: Tập nghiệm của phương trình ban đầu là hợp của các tập nghiệm trên từng khoảng. Đây cũng là điều cần chú ý khi giải một bất phương trình chứa ẩn trong dấu giá trị tuyệt đối.
| VÍ DỤ 5 |
Giải
bất
phương
trình
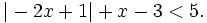
|
| Lời giải |
Theo
định
nghĩa
giá
trị
tuyệt
đối
ta
có:
Từ đó ta có bảng khử dấu giá trị tuyệt đối sau: Giải các hệ bất phương trình: Nghiệm của bất phương trình đã cho là hợp của hai khoảng: ![\left(-7;{\frac 12}\right]\cup \left({\frac 12};3\right)=(-7;3)](https://tusach.thuvienkhoahoc.com/images/math/7/5/6/75636048c6e2268929e11d1ffcf0b219.png) |
CHÚ
Ý:
- Bằng cách áp dụng tính chất của giá trị tuyệt đối ta có thể dễ dàng giải các bất phương trình dạng |f(x)| ≤ a và |f(x)| ≥ a với a > 0 đã cho.
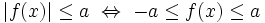
|
BÀI TẬP[sửa]
1. Xét dấu các biểu thức:
| a) f(x) = (2x - 1)(x + 3); | b) f(x) = (-3x - 3)(x + 2)(x + 3); |
c)
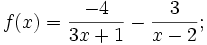
|
d) f(x) = 4x2 - 1. |
- Hướng dẫn Bài 1d): Phân tích đa thức thành nhân tử bậc nhất rồi xét dấu.
2.
Giải
các
bất
phương
trình
a)
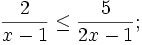
|
b)
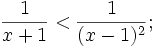
|
c)
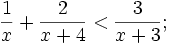
|
d)
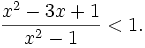
|
3.
Giải
các
bất
phương
trình
a)
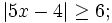
|
b)
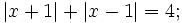
|
c)
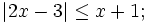
|
d)
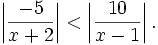
|
-
Hướng
dẫn
Bài
3d):
Với
x
≠
-2
và
x
≠
1
thì
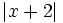 và
và
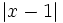 đều
dương,
nên
nhân
cả
hai
vế
của
bất
phương
trình
với
tích:
đều
dương,
nên
nhân
cả
hai
vế
của
bất
phương
trình
với
tích:
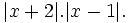
____________________________
Làm thêm
4.
Giải
và
biện
luận
các
bất
phương
trình
sau:
| a) m(x - m) ≤ x - 1; | b) (m + 1)x + m < 3x + 4; |
c)
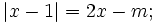
|
d)
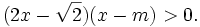
|
5.
Xét
dấu
các
biểu
thức
sau:
| a) -x2 + x + 6 |
b)
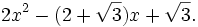
|
6.
Giải
các
bất
phương
trình:
a)
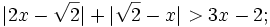
|
b)
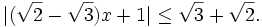
|
7.
Giải
các
hệ
bất
phương
trình:
a)
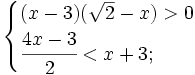
|
b)
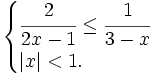
|
Tài liệu tham khảo[sửa]
-
Sách
in:
- Đại số 10, Nhà xuất bản Giáo dục, 2006, trang 87.
- Đại số 10 Nâng cao, Nhà xuất bản Giáo dục, 2006, trang 122.
- Đại số 10, Nhà xuất bản Giáo dục, 2001, trang 81.
- Tài liệu giáo khoa thí điểm, Đại số 10, Ban khoa học tự nhiên, Nhà xuất bản Giáo dục, 2006, trang 130.



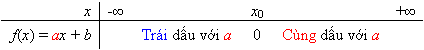
 .
Do
đó,
dấu
của
nó
được
cho
trong
bảng
sau:
.
Do
đó,
dấu
của
nó
được
cho
trong
bảng
sau:
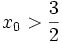 và
âm
khi
và
âm
khi
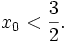
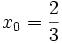 .
Suy
ra
bảng
dấu:
.
Suy
ra
bảng
dấu: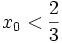 và
âm
khi
và
âm
khi
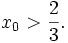
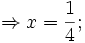 x
+
2
=
0
x
+
2
=
0
 x
=
-2;
-3x
+
5
=
0
x
=
-2;
-3x
+
5
=
0
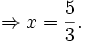
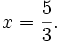
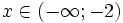 hoặc
hoặc
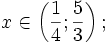
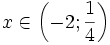 hoặc
hoặc
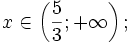
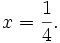
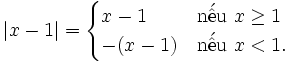

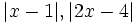 và
phương
trình
(1):
và
phương
trình
(1):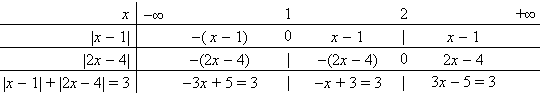
 -3x
+
5
=
3
-3x
+
5
=
3
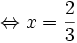 (tmđk:
x
<
1).
(tmđk:
x
<
1).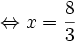 (tmđk:
x
≥
2).
(tmđk:
x
≥
2). và
và