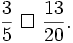Đại số 8/Chương IV/§1. Liên hệ giữa thứ tự và phép cộng
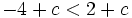 với
mọi
số
c?
với
mọi
số
c? |
Mục lục
Lí thuyết[sửa]
Nhắc lại về thứ tự trên tập hợp số[sửa]
Trên tập hợp số thực, khi so sánh hai số a và b, xảy ra một trong ba trường hợp sau:
- Số a bằng số b, kí hiệu a = b.
- Số a nhỏ hơn b, kí hiệu a < b.
- Số a lớn hơn b, kí hiệu a > b.
Khi biểu diễn số thực trên trục số (vẽ theo phương nằm ngang), điểm biểu diễn số nhỏ hơn ở bên trái điểm biểu diễn số lớn hơn. Chính điều đó cho ta hình dung về thứ tự trên tập số thực.
| Hoạt động 1 |
Điền
dấu
thích
hợp
(=,
<,
>)
vào
ô
vuông:
a)
1,53
c)
|
Nếu
số
a
không
nhỏ
hơn
số
b,
thì
phải
có
hoặc
a
>
b,
hoặc
a
=
b.
Khi
đó,
ta
nói
gọn
là
a
lớn
hơn
hoặc
bằng
b,
kí
hiệu
là
a
≥
b.
- Ví dụ: x2 ≥ 0 với mọi x.
Nếu c là số không âm thì ta viết c ≥ 0.
Nếu
số
a
không
lớn
hơn
số
b,
thì
phải
có
hoặc
a
<
b,
hoặc
a
=
b.
Khi
đó,
ta
nói
gọn
là
a
nhỏ
hơn
hoặc
bằng
b,
kí
hiệu
là
a
≤
b.
- Ví dụ: -x2 ≤ 0 với mọi x.
Nếu d là số không lớn hơn 3 thì ta viết d ≤ 3.
Bất đẳng thức[sửa]
Ta gọi hệ thức dạng a < b (hay a > b, a ≤ b, a ≥ b) là bất đẳng thức và gọi a là vế trái, b là vế phải của bất đẳng thức.
Liên hệ giữa thứ tự và phép cộng[sửa]
Tính chất: Với ba số a, b và c, ta có:
- Nếu a < b thì a + c < b + c; Nếu a ≤ b thì a + c ≤ b + c;
- Nếu a > b thì a + c > b + c; Nếu a ≥ b thì a + c ≥ b + c;
Hai bất đẳng thức "-2 < 3" và "-4 < 2" (hay 5 > 1 và -3 > -7) được gọi là hai bất đẳng thức cùng chiều.
|
Khi
cộng
cùng
một
số
vào
cả
hai
vế
của
một
bất
đẳng
thức
ta
được
bất
đẳng
thức
mới
cùng
chiều
với
bất
đẳng
thức
đã
cho.
|
|
Có
thể
áp
dụng
tính
chất
trên
để
so
sánh
hai
số,
hoặc
chứng
minh
bất
đẳng
thức.
Ví
dụ
2.
Chứng
tỏ
2003
+
(-35)
<
2004
+
(-35).
Giải:
Theo tính chất trên, cộng -35 vào cả hai vế của bất đẳng thức 2003 < 2004, ta suy ra 2003 + (-35) < 2004 + (-35).
BÀI TẬP[sửa]
Tài liệu tham khảo[sửa]
- Sách in: Toán 8, tập 2, nhà xuất bản Giáo dục, 2004, trang 35, 36.



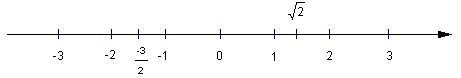
 1,8
b)
-2,37
1,8
b)
-2,37
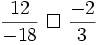 d)
d)