Đại số 8/Chương IV/§4. Bất phương trình bậc nhất một ẩn
Với
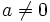 ,
nếu
,
nếu
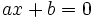 thì
thì
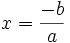 .
Thế
còn
.
Thế
còn
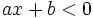 thì
thì
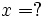
|
Mục lục
Lí thuyết[sửa]
Định nghĩa[sửa]
|
Bất
phương
trình
dạng:
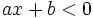
|
|
| Hoạt động 1 |
Trong
các
bất
phương
trình
sau,
hãy
cho
biết
bất
phương
trình
nào
là
bất
phương
trình
bậc
nhất
một
ẩn:
a) 2x - 3 < 0; b) 0.x + 5 > 0; c) 5x - 15 ≥ 0; d) x2 > 0. |
Hai quy tắc biến đổi bất phương trình[sửa]
Quy tắc chuyển vế[sửa]
Từ liên hệ giữa thứ tự và phép cộng, ta có quy tắc sau (gọi là quy tắc chuyển vế) để biến đổi tương đương bất phương trình:
|
Khi
chuyển
vế
một
hạng
tử
của
bất
phương
trình
từ
vế
này
sang
vế
kia
ta
phải
đổi
dấu
hạng
tử
đó.
|
|
| VÍ DỤ 1 |
Giải
các
bất
phương
trình
sau:
a) x - 5 < 18; b) 3x > 2x + 5 (có biểu diễn tập nghiệm trên trục số). |
| Lời giải |
a)
Ta
có:
Vậy
tập
nghiệm
của
bất
phương
trình
là
Vậy
tập
nghiệm
của
bất
phương
trình
là
Tập nghiệm này được biểu diễn trên trục số như sau:
|
| Hoạt động 2 |
Giải
các
bất
phương
trình
sau:
a) x + 12 > 21; b) -2x > -3x - 5. |
Quy tắc nhân với một số[sửa]
Từ liên hệ giữa thứ tự và phép nhân, ta có quy tắc sau (gọi là quy tắc nhân) để biến đổi tương đương bất phương trình:
|
Khi
nhân
hai
vế
của
bất
phương
trình
với
cùng
một
số
khác
0,
ta
phải:
|
|
| VÍ DỤ 2 |
Giải
các
bất
phương
trình
sau:
a)
0,5x
<
3;
b)
|
| Lời giải |
a)
Ta
có:
Vậy
tập
nghiệm
của
bất
phương
trình
là
Vậy
tập
nghiệm
của
bất
phương
trình
là
Tập nghiệm này được biểu diễn trên trục số như sau:
|
| Hoạt động 3 |
Giải
các
bất
phương
trình
sau
(dùng
quy
tắc
nhân):
a) 2x < 24; b) -3x < 27. |
| Hoạt động 4 |
Giải
thích
sự
tương
đương:
a)
x
+
3
<
7
|
Giải bất phương trình bậc nhất một ẩn[sửa]
| VÍ DỤ 3 |
Giải
bất
phương
trình
2x
-
3
<
0
và
biểu
diễn
tập
nghiệm
trên
trục
số.
|
| Lời giải |
Ta
có:
Vậy
tập
nghiệm
của
bất
phương
trình
là
|
| Hoạt động 5 |
Giải
bất
phương
trình
-4x
-
8
<
0
và
biểu
diễn
tập
nghiệm
trên
trục
số.
|
-
-
-
-
CHÚ
Ý:
Để
cho
gọn
khi
trình
bày,
ta
có
thể:
- Không ghi câu giải thích;
- Khi có kết quả x < 1,5 (ở ví dụ 3) thì coi là giải xong và viết đơn giản:
-
- "Nghiệm của bất phương trình 2x - 3 < 0 là x < 1,5".
-
CHÚ
Ý:
Để
cho
gọn
khi
trình
bày,
ta
có
thể:
-
-
| VÍ DỤ 4 |
Giải
bất
phương
trình
-4x
+
12
<
0.
|
| Lời giải |
Ta
có:
Vậy nghiệm của bất phương trình là x > 3. |
Giải bất phương trình đưa được về dạng bậc nhất một ẩn[sửa]
| VÍ DỤ 5 |
Giải
bất
phương
trình
3x
+
5
<
5x
-
7.
|
| Lời giải |
Ta
có:
Vậy nghiệm của bất phương trình là x > 6. |
| Hoạt động 6 |
Giải
bất
phương
trình
-0,2x
-
0,2
>
0,4x
-
2.
|
BÀI TẬP[sửa]
8. Hình vẽ sau biểu diễn tập nghiệm của bất phương trình nào? (Kể ba bất phương trình có cùng tập nghiệm).
a)
b)
9.
Kiểm
tra
xem
giá
trị
x
=
-2
có
là
nghiệm
của
bất
phương
trình
sau
không:
a)
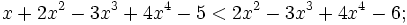
b)
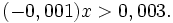
Xem thêm[sửa]
Tài liệu tham khảo[sửa]
- Sách in: Toán 8, tập 2, Nhà xuất bản Giáo dục, 2004, trang 43.



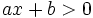 ,
,
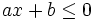 ,
,
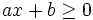 )
) x
<
18
+
5
(Chuyển
vế
-5
và
đổi
dấu
thành
5)
x
<
18
+
5
(Chuyển
vế
-5
và
đổi
dấu
thành
5)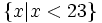 .
.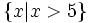 .
.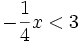 (có
biểu
diễn
tập
nghiệm
trên
trục
số).
(có
biểu
diễn
tập
nghiệm
trên
trục
số).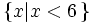 .
.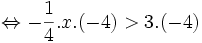 (Nhân
cả
hai
vế
với
-4
và
đổi
chiều)
(Nhân
cả
hai
vế
với
-4
và
đổi
chiều)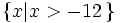 .
.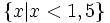 và
được
và
được


