Chủ đề nóng: Phương pháp kỷ luật tích cực - Cổ học tinh hoa - Những thói hư tật xấu của người Việt - Công lý: Việc đúng nên làm - Giáo án Điện tử - Sách giáo khoa - Học tiếng Anh - Bài giảng trực tuyến - Món ăn bài thuốc - Chăm sóc bà bầu - Môi trường - Tiết kiệm điện - Nhi khoa - Ung thư - Tác hại của thuốc lá - Các kỹ thuật dạy học tích cực
- Dạy học phát triển năng lực - Chương trình giáo dục phổ thông
Bài tập Điện động lực học
Từ VLOS
Mục lục
Nhắc lại vài kiến thức[sửa]
Trường vô hướng/vecto[sửa]
Phép tính vecto - curl (rot) và div[sửa]
Toán
tử
divergence
(div)
xác
định
trên
một
trường
vecto
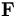 được
định
nghĩa
bởi:
được
định
nghĩa
bởi:
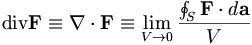 .
.
Trong hệ tọa độ Cartesian, toán tử này được viết:
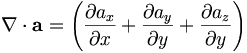 .
.
Toán
tử
curl
(rot),
giống
như
toán
tử
div,
xác
định
trên
trường
vecto
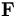 bởi
định
nghĩa
bởi
định
nghĩa
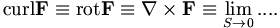 .
.
Định lý Green[sửa]
Định lý Stokes[sửa]
Hệ phương trình Maxwell[sửa]
| Tên | Dạng phương trình vi phân | Dạng tích phân |
|---|---|---|
| Định luật Gauss: |
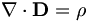 |
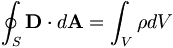 |
|
Đinh
luật
Gauss
cho
từ
trường (sự không tồn tại của từ tích): |
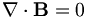 |
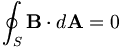 |
| Định luật Faraday cho từ trường: |
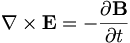 |
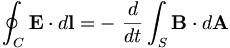 |
|
Định
luật
Ampere (với sự bổ sung của Maxwell): |
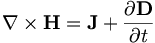 |
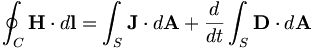 |
Khởi thảo: MucDong


