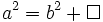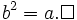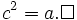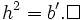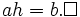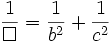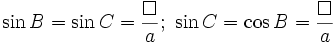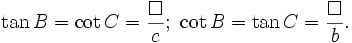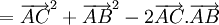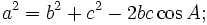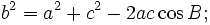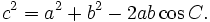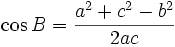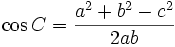Hình học 10/Chương II/§3. Các hệ thức lượng trong tam giác và giải tam giác
Chúng ta biết rằng một tam giác hoàn toàn được xác định (nghĩa là hoàn toàn tìm được số đo các cạnh, các góc còn lại của tam giác này) nếu biết:
- ba cạnh hoặc
- hai cạnh và góc xen giữa hoặc
- một cạnh và hai góc kề
Như vậy, giữa các yếu tố của tam giác có những mối liên hệ nào đó, mà ta sẽ gọi chúng là các hệ thức lượng trong tam giác. Trong bài này, chúng ta sẽ tìm hiểu một số hệ thức đó.
Mục lục
Lí thuyết[sửa]
| Hoạt động 1 | |
Xét hệ thức (1.):
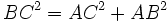 (1*)
(1*)
đây
chính
là
nội
dung
định
lí
Pitago
trong
tam
giác
vuông
ABC
(vuông
A).
Mặt
khác,
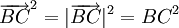 nên
hệ
thức
(1*)
trở
thành:
nên
hệ
thức
(1*)
trở
thành:
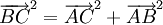 (2*)
(2*)Nếu có thể viết định lí Pitago dưới dạng các vectơ, thì có thể chứng minh định lí Pitago (2*) bằng các tính chất của vectơ"?
Thật vậy, bằng các kiến thức đã biết về vectơ ta có thể chứng minh ngắn ngọn đẳng thức (2*) như sau:
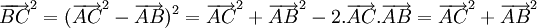
Như
vậy,
trong
tam
giác
vuông
bằng
cách
viết
độ
dài
một
cạnh
(BC)
dưới
dạng
vectơ
(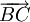 )
rồi
bình
phương
nó
lên
và
sử
dụng
các
tính
chất
của
vectơ
thì
ta
được
định
lí
Pitago.
Tò
mò
hơn
chút,
bạn
cũng
có
thể
làm
như
thế
nhưng
trong
một
tam
giác
bất
kì
thì
bạn
cũng
sẽ
nhận
được
một
hệ
thức.
)
rồi
bình
phương
nó
lên
và
sử
dụng
các
tính
chất
của
vectơ
thì
ta
được
định
lí
Pitago.
Tò
mò
hơn
chút,
bạn
cũng
có
thể
làm
như
thế
nhưng
trong
một
tam
giác
bất
kì
thì
bạn
cũng
sẽ
nhận
được
một
hệ
thức.
Hệ thức gì vậy?
Định lí côsin trong tam giác[sửa]
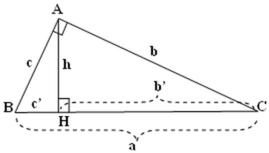
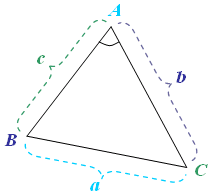
Bài toán: Trong tam giác ABC cho biết hai cạnh AB, AC và góc A. Hãy tính cạnh BC.
GIẢI
Ta
có
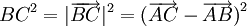
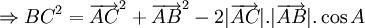
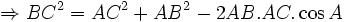
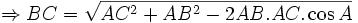
Từ
kết
quả
của
bài
toán
trên
được
định
lí
sau,
gọi
là
định
lí
côsin
trong
tam
giác:
Định lí Côsin
Định lí trên cho ta cách tính độ dài một cạnh của một tam giác khi biết hai cạnh còn lại và côsin góc xen giữa hai cạnh đó.
- Trong một tam giác, bình phương một cạnh bằng tổng bình phương hai cạnh còn lại trừ đi hai lần tích hai cạnh với côsin góc xen giữa hai cạnh đó.
Hệ quả
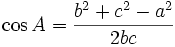
|
Định lí sin trong tam giác[sửa]
Định lí đường trung tuyến trong tam giác[sửa]
Các hệ thức tính diện tích trong tam giác[sửa]
Giải tam giác và ứng dụng thực tế[sửa]
BÀI TẬP[sửa]
Tài liệu tham khảo[sửa]
-
Sách
in:
- Hình học 10, Nhà xuất bản giáo dục, 2006, trang 46.
- Hình học 10 Nâng cao, Nhà xuất bản giáo dục, 2006, trang 53.
- Hình học 10, Nhà xuất bản giáo dục, 2001, trang 45.
- Tài liệu giáo khoa thí điểm, Hình học 10, Ban khoa học tự nhiên, Nhà xuất bản giáo dục, 1996, trang 35.