Tính tỷ lệ

Từ VLOS
(đổi hướng từ Tính Tỷ lệ)
Bước tới: chuyển hướng, tìm kiếm

Tỷ lệ là biểu thức toán học để so sánh hai hay nhiều số với nhau. Tỷ lệ có thể được dùng để so sánh các đại lượng và số lượng tuyệt đối hoặc so sánh các phần với một tổng. Tỷ lệ có thể được tính và viết dưới các dạng khác nhau, tuy nhiên, nguyên lý hướng dẫn cách sử dụng tỷ lệ là giống nhau.

Các bước[sửa]

Hiểu Thế nào là Tỷ lệ[sửa]

  1. Chú ý cách tỷ lệ được sử dụng. Tỷ lệ được sử dụng trong học thuật và cuộc sống để so sánh nhiều đại lượng hoặc số lượng với nhau. Tỷ lệ đơn giản nhất là so sánh hai giá trị, ngoài ra còn có tỷ lệ so sánh từ ba giá trị trở lên. Trong bất cứ trường hợp nào phải so sánh giữa hai số và đại lượng khác nhau trở lên thì tỷ lệ đều được áp dụng. Bằng cách mô tả mối quan hệ về số lượng, tỷ lệ cho biết liệu công thức hóa học có thể tăng gấp đôi hay công thức nấu ăn có thể được bổ sung hay không. Khi đã hiểu được vấn đề, bạn sẽ thường xuyên sử dụng tỷ lệ trong cuộc sống của mình.[1]
  2. Hiểu tỷ lệ là gì. Như đã lưu ý ở trên, tỷ lệ thể hiện mối quan hệ về lượng của ít nhất hai vật với nhau. Ví dụ, nếu làm bánh cần hai chén bột mỳ và một chén đường, bạn sẽ nói là tỷ lệ bột mỳ so với đường là 2/1.
    • Tỷ lệ được sử dụng để xác định mối quan hệ giữa các đại lượng với nhau, thậm chí nếu chúng không ràng buộc trực tiếp với nhau (chẳng hạn như trong công thức nấu ăn). Ví dụ, nếu có 5 học sinh nữ và 10 học sinh nam trong lớp, tỷ lệ học sinh nữ so với học sinh nam là 5/10. Hai đại lượng này không phụ thuộc hay ràng buộc với nhau, và sẽ thay đổi nếu bớt hoặc thêm số học sinh. Tỷ lệ đơn giản là để so sánh các đại lượng.
  3. Để ý các cách tỷ lệ được viết. Tỷ lệ có thể được viết bằng chữ hoặc bằng ký hiệu toán học.[2]
    • Bạn sẽ thường xuyên thấy tỷ lệ được viết bằng chữ (như ở trên). Do tỷ lệ thường được sử dụng theo nhiều cách khác nhau, nếu không làm việc trong lĩnh vực khoa học hoặc toán học, thì bạn sẽ thấy đó là cách viết tỷ lệ phổ biến nhất.
    • Tỷ lệ thường được dùng với dấu hai chấm. Khi so sánh hai đại lượng, bạn sẽ dùng dấu hai chấm (như 7 : 13) và khi so sánh hai đại lượng trở lên, bạn thêm dấu hai chấm vào giữa từng cặp đại lượng liên tục (như 10 : 2 : 23). Trong ví dụ về lớp học, ta có thể so sánh số học sinh nam với số học sinh nữ bằng tỷ lệ: 5 nữ : 10 nam. Ta cũng có thể viết đơn giản là: 5 : 10.
    • Tỷ lệ đôi khi được viết dưới dạng phân số. Trong ví dụ về lớp học, tỷ lệ 5 học sinh nữ và 10 học sinh nam có thể được viết đơn giản là 5/10. Tuy nhiên, bạn không nên hiểu tỷ lệ đó giống như một phân số và phải nhớ rằng các số này không thể hiện tỷ lệ giữa một phần so với một tổng.

Sử dụng Tỷ lệ[sửa]

  1. Đưa tỷ lệ về dạng tối giản. Tỷ lệ có thể được tối giản giống như phân số bằng cách loại bỏ ước số chung của các số hạng trong tỷ lệ. Để tối giản tỷ lệ, chia số hạng trong tỷ lệ cho các ước số chung đến khi không thể chia được nữa. Tuy nhiên, khi thực hiện, điều quan trọng là không được quên đại lượng ban đầu để có được tỷ lệ đó.[3]
    • Trong ví dụ về lớp học nêu trên, tỷ lệ 5 học sinh nữ so với 10 học sinh nam (5 : 10), cả hai số hạng đều có ước số chung là 5. Chia hai số hạng cho 5 (ước số chung lớn nhất) để được tỷ lệ 1 học sinh nữ so với 2 học sinh nam (hay 1 : 2). Tuy nhiên, ta phải ghi nhớ đại lượng ban đầu ngay cả khi sử dụng tỷ lệ đã được tối giản. Lớp học có số học sinh là 15 chứ không phải là 3. Tỷ lệ tối giản chỉ so sánh mối quan hệ giữa số học sinh nam và nữ. Cứ 2 học sinh nam có 1 học sinh nữ chứ không phải là chỉ có 2 học sinh nam và 1 học sinh nữ.
    • Một số tỷ lệ không thể tối giản. Ví dụ, 3 : 56 không thể tối giản vì hai số không có ước số chung - 3 là số nguyên tố, và 56 không chia hết cho 3.
  2. Dùng phép nhân hoặc chia để "cân bằng" tỷ số. Một dạng bài toán sử dụng tỷ số thường thấy là dùng tỷ số để cân bằng tăng hoặc giảm hai số tỷ lệ với nhau. Nhân hoặc chia các số hạng trong tỷ số với cùng một số để được tỷ số mới tỷ lệ với tỷ số ban đầu, vì vậy, để cân bằng tỷ số, hãy nhân hoặc chia tỷ số với hệ số tỷ lệ.[4]
    • Ví dụ, một thợ làm bánh cần tăng công thức làm bánh lên 3 lần. Nếu tỷ lệ bột mỳ so với đường thông thường là 2/1 (2 : 1), thì cả hai số sẽ phải nhân với 3. Số lượng tương ứng sẽ là 6 chén bột mỳ với 3 chén đường (6 : 3).
    • Quy trình tương tự có thể làm ngược lại. Nếu thợ làm bánh chỉ cần một nửa nguyên liệu làm công thức bánh thông thường thì cả hai đại lượng đều nhân với 1/2 (hay chia cho 2). Kết quả sẽ là 1 chén bột mỳ so với 1/2 (0,5) chén đường.
  3. Tìm ẩn số biết trước hai tỷ số bằng nhau. Một dạng bài toán khác về tỷ số yêu cầu tìm một ẩn trong tỷ số, cho trước một số khác trong tỷ số và tỷ số thứ hai bằng với tỷ số thứ nhất. Nguyên tắc nhân chéo có thể giải bài toán này khá dễ dàng. Viết tỷ số dưới dạng phân số, đặt hai tỷ số bằng nhau và nhân chéo để ra kết quả.[5]
    • Ví dụ, ta có một nhóm học sinh gồm 2 nam và 5 nữ. Nếu tính tỷ lệ nam trên nữ thì một lớp với 20 học sinh nữ sẽ có bao nhiêu học sinh nam? Để giải bài toán này, đầu tiên, ta có hai tỷ số, một tỷ số chứa ẩn số: 2 nam : 5 nữ = x nam : 20 nữ. Chuyển thành phân số, ta có 2/5 và x/20. Nếu nhân chéo lên, ta được 5x=40, giải bài toán bằng cách chia hai vế phương trình cho 5. Kết quả cuối cùng là x=8.

Phát hiện Lỗi[sửa]

  1. Tránh cộng hoặc trừ trong các bài toán tỷ lệ dạng chữ. Nhiều bài toán dạng chữ có cách viết như sau: "Một công thức nấu ăn cần 4 củ khoai tây và 5 củ cà rốt. Nếu bạn cần dùng 8 củ khoai tây thì số cà rốt phải có để giữ nguyên tỷ lệ là bao nhiêu?" Nhiều học sinh cộng thêm một lượng tương tự vào từng đại lượng. Thực ra bạn cần dùng phép nhân, không phải là phép cộng để giữ nguyên tỷ lệ. Dưới đây là ví dụ về cách làm đúng và sai khi giải bài toán này:
    • Cách làm sai: "8 - 4 = 4, ta cộng 4 củ khoai tây và công thức nấu ăn. Có nghĩa là ta cũng sẽ cộng thêm 4 củ cà rốt vào 5 củ cho sẵn… Đợi đã! Đó không phải là cách đúng. Ta sẽ thử lại".
    • Cách làm đúng: "8 ÷ 4 = 2, ta nhân số củ khoai tây với 2. Điều đó có nghĩa là ta cũng nhân 5 củ cà rốt với 2. 5 x 2 = 10, vậy ta cần tổng số 10 củ cà rốt cho công thức nấu ăn mới".
  2. Đổi về cùng một đơn vị. Một số bài toán ra đề rắc rối hơn bằng cách dùng nhiều đơn vị tính khác nhau. Hãy đổi về cùng một đơn vị trước khi tìm tỷ số. Dưới đây là ví dụ về một bài toán và cách giải:
    • Một người coi kho có 500 g vàng và 10 kg bạc. Hỏi tỷ lệ vàng so với bạc trong kho là bao nhiêu?
    • Gram và kilogram không giống nhau, nên ta phải đổi đơn vị. 1 kg = 1.000 g, vậy 10 kg = 10 kg x 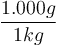{\frac {1.000g}{1kg}} = 10 x 1.000 g = 10.000 g.
    • Người coi kho có 500 g vàng và 10.000 g bạc.
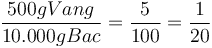    • Tỷ lệ vàng trên bạc là {\frac {500gVang}{10.000gBac}}={\frac {5}{100}}={\frac {1}{20}} .
  3. Ghi đơn vị trong bài toán. Trong những bài toán tỷ lệ dạng chữ, bạn sẽ dễ làm sai hơn khi ghi đơn vị tính sau mỗi giá trị. Hãy nhớ, đơn vị tính giống nhau sẽ không được ghi trên tỷ số. Sau khi tối giản tỷ số, bạn hãy thêm đơn vị tính vào kết quả cuối cùng.
    • Ví dụ: Nếu bạn có 6 hộp, cứ 3 hộp có 9 viên bi, hỏi có tất cả bao nhiêu viên bi?
    • Cách làm sai: 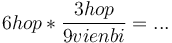6hop*{\frac {3hop}{9vienbi}}=... Khoan đã, không có gì bị gạch bỏ, kết quả sẽ là "hộp x hộp / viên bi". Như vậy không hợp lý.
    • Cách làm đúng:
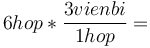
      6hop*{\frac {9vienbi}{3hop}}= 6hop*{\frac {3vienbi}{1hop}}=

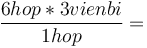
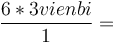      {\frac {6hop*3vienbi}{1hop}}= {\frac {6*3vienbi}{1}}= 18 viên bi.

Nguồn và Trích dẫn[sửa]

  1. ↑ http://www.virtualnerd.com/common-core/grade-6/6_RP-ratios-proportional-relationships/A
  2. ↑ http://www.purplemath.com/modules/ratio.htm
  3. ↑ http://www.helpwithfractions.com/math-homework-helper/least-common-denominator/
  4. ↑ http://www.mathplanet.com/education/algebra-1/how-to-solve-linear-equations/ratios-and-proportions-and-how-to-solve-them
  5. ↑ http://www.math.com/school/subject1/lessons/S1U2L2DP.html
  • « Mới nhất
  • ‹ Mới hơn
  • Cũ hơn ›

Liên kết đến đây

Lấy từ “https://tusach.thuvienkhoahoc.com/index.php?title=Tính_tỷ_lệ&oldid=128864”