Chủ đề nóng: Phương pháp kỷ luật tích cực - Cổ học tinh hoa - Những thói hư tật xấu của người Việt - Công lý: Việc đúng nên làm - Giáo án Điện tử - Sách giáo khoa - Học tiếng Anh - Bài giảng trực tuyến - Món ăn bài thuốc - Chăm sóc bà bầu - Môi trường - Tiết kiệm điện - Nhi khoa - Ung thư - Tác hại của thuốc lá - Các kỹ thuật dạy học tích cực
- Dạy học phát triển năng lực - Chương trình giáo dục phổ thông
Tính hệ số góc, tung và hoành độ gốc của đường thẳng
Từ VLOS
Hệ số góc của một đường đo lường độ dốc của nó.[1] Bạn cũng có thể nói rằng đó là thay đổi dọc (rise) trên thay đổi ngang (run) hay độ đi lên của đường theo chiều thẳng đứng so với độ di chuyển của nó theo chiều ngang. Tìm hệ số góc của một đường hay sử dụng hệ số góc đó để tìm các điểm nằm trên đường thẳng là những kỹ năng quan trọng trong kinh tế,[2] khoa học địa chất,[3] kế toán/tài chính và nhiều lĩnh vực khác.
Mục lục
Các bước[sửa]
- Làm quen với hình cơ bản:
Tìm hệ số góc bằng đồ thị[sửa]
-
Chọn
hai
điểm
trên
đường
thẳng.
Biểu
diễn
và
ghi
tọa
độ
của
chúng
trên
đồ
thị.
- Nhớ rằng, hoành độ đứng trước và tung độ đứng sau.
- Ví dụ, bạn có thể chọn điểm (-3, -2) và (5, 4).
-
Xác
định
thay
đổi
dọc
giữa
hai
điểm.
Để
làm
điều
này,
bạn
phải
so
sánh
sự
khác
biệt
tung
độ
hai
điểm.
Bắt
đầu
với
điểm
đầu
tiên,
là
điểm
nằm
xa
về
phía
bên
trái
của
đồ
thị,
và
dịch
chuyển
cho
đến
khi
gặp
tung
độ
của
điểm
thứ
hai.
- Thay đổi dọc có thể dương hoặc âm, nghĩa là bạn có thể dịch lên hoặc xuống.[4] Nếu đường của chúng ta di chuyển lên và qua bên phải, thay đổi tung độ sẽ dương. Nếu đường này di chuyển xuống và qua phải, thay đổi dọc là âm.[1]
- Ví dụ, nếu tung độ của điểm đầu tiên là (-2) và điểm thứ hai là (-4), bạn sẽ cộng thêm 6 điểm hay thay đổi dọc của bạn là 6.
-
Xác
định
thay
đổi
ngang
giữa
hai
điểm.
Để
làm
điều
này,
bạn
phải
so
sánh
sự
khác
biệt
giữa
hoành
độ
hai
điểm.
Bắt
đầu
với
điểm
đầu
tiên,
là
điểm
xa
nhất
bên
trái
đồ
thị,
và
tiến
tới
cho
đến
khi
có
được
hoành
độ
của
điểm
thứ
hai.
- Thay đổi ngang luôn dương, nghĩa là bạn chỉ có thể đi từ trái sang phải mà không bao giờ là ngược lại.[4]
- Ví dụ, nếu hoành độ của điểm đầu là (-3) và điểm thứ hai là (5), bạn sẽ phải cộng thêm 8, nghĩa là thay đổi ngang của bạn là 8.
-
Tính
tỉ
số
thay
đổi
ngang
trên
thay
đổi
dọc
để
xác
định
hệ
số
góc.
Hệ
số
góc
thường
có
dạng
phân
số
nhưng
cũng
có
trường
hợp
nó
là
số
nguyên.
-
Ví
dụ,
nếu
thay
đổi
dọc
là
6
và
thay
đổi
ngang
là
8
thì
hệ
số
góc
của
bạn
là
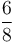 .
Rút
gọn
ta
được:
.
Rút
gọn
ta
được:
 .
.
-
Ví
dụ,
nếu
thay
đổi
dọc
là
6
và
thay
đổi
ngang
là
8
thì
hệ
số
góc
của
bạn
là
Tìm hệ số góc bằng hai điểm cho trước[sửa]
-
Thiết
lập
công
thức
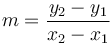 .
Trong
đó,
m
=
hệ
số
góc,
.
Trong
đó,
m
=
hệ
số
góc,
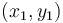 =
tọa
độ
của
điểm
thứ
nhất,
=
tọa
độ
của
điểm
thứ
nhất,
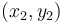 =
tọa
độ
của
điểm
thứ
hai.
=
tọa
độ
của
điểm
thứ
hai.
-
Nhớ
rằng
hệ
số
góc
bằng
thay
đổi
dọc
trên
thay
đổi
ngang
hay
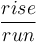 .
Bạn
đang
sử
dụng
công
thức
để
tính
thay
đổi
tung
độ
(dọc)
trên
thay
đổi
hoành
độ
(ngang).[5]
.
Bạn
đang
sử
dụng
công
thức
để
tính
thay
đổi
tung
độ
(dọc)
trên
thay
đổi
hoành
độ
(ngang).[5]
-
Nhớ
rằng
hệ
số
góc
bằng
thay
đổi
dọc
trên
thay
đổi
ngang
hay
-
Thế
tọa
độ
vào
công
thức.
Đảm
bảo
rằng
bạn
đã
thế
tọa
độ
điểm
thứ
nhất
(
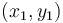 )
và
điểm
thứ
hai
(
)
và
điểm
thứ
hai
(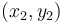 )
vào
đúng
vị
trí
trong
công
thức.
Bằng
không,
hệ
số
góc
thu
được
sẽ
không
chính
xác.
)
vào
đúng
vị
trí
trong
công
thức.
Bằng
không,
hệ
số
góc
thu
được
sẽ
không
chính
xác.
-
Ví
dụ,
với
hai
điểm
(-3,
-2)
và
(5,
4),
công
thức
của
bạn
sẽ
là:
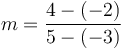 .
.
-
Ví
dụ,
với
hai
điểm
(-3,
-2)
và
(5,
4),
công
thức
của
bạn
sẽ
là:
-
Thực
hiện
phép
tính
và
rút
gọn
nếu
có
thể.
Bạn
sẽ
thu
được
hệ
số
góc
ở
dạng
phân
số
hoặc
số
nguyên.
-
Ví
dụ,
nếu
hệ
số
góc
của
bạn
là
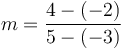 ,
bạn
nên
đặt
,
bạn
nên
đặt
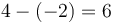 ở
mẫu
số
(Nhớ
rằng
khi
trừ
số
âm,
bạn
cộng)
và
ở
mẫu
số
(Nhớ
rằng
khi
trừ
số
âm,
bạn
cộng)
và
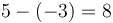 ở
tử
số.
Bạn
có
thể
rút
gọn
ở
tử
số.
Bạn
có
thể
rút
gọn
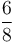 thành
thành
 và
do
đó:
và
do
đó:
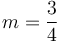 .
.
-
Ví
dụ,
nếu
hệ
số
góc
của
bạn
là
Tìm tung độ gốc khi biết hệ số góc và một điểm[sửa]
-
Thiết
lập
công
thức
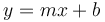 .
Trong
đó,
y
=
tung
độ
của
điểm
bất
kỳ
trên
đường,
m
=
hệ
số
góc,
x
=
hoành
độ
của
điểm
bất
kỳ
trên
đường
thẳng
và
b
=
tung
độ
gốc.
.
Trong
đó,
y
=
tung
độ
của
điểm
bất
kỳ
trên
đường,
m
=
hệ
số
góc,
x
=
hoành
độ
của
điểm
bất
kỳ
trên
đường
thẳng
và
b
=
tung
độ
gốc.
-
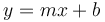 là
phương
trình
của
một
đường
thẳng.
[6]
là
phương
trình
của
một
đường
thẳng.
[6] - Tung độ gốc là điểm mà tại đó, đường thẳng cắt trục tung.
-
-
Thế
giá
trị
hệ
số
góc
và
tọa
độ
của
một
điểm
trên
đường
thẳng.
Nhớ
rằng,
hệ
số
góc
bằng
thay
đổi
dọc
trên
thay
đổi
ngang.
Nếu
cần
tìm
hệ
số
góc,
hãy
tham
khảo
hướng
dẫn
ở
trên.
-
Ví
dụ,
nếu
hệ
số
góc
là
 và
(5,4)
là
một
điểm
trên
đường
thẳng,
vậy
công
thức
thu
được
là:
và
(5,4)
là
một
điểm
trên
đường
thẳng,
vậy
công
thức
thu
được
là:
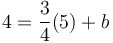 .
.
-
Ví
dụ,
nếu
hệ
số
góc
là
-
Hoàn
thành
và
giải
phương
trình,
tìm
b.
Đầu
tiên,
nhân
hệ
số
góc
và
hoành
độ.
Trừ
hai
vế
cho
tích
này,
ta
thu
được
b.
-
Trong
bài
toán
ví
dụ,
phương
trình
trở
thành:
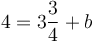 .
Trừ
hai
vế
cho
.
Trừ
hai
vế
cho
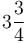 ,
ta
thu
được
,
ta
thu
được
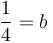 .
Vậy,
tung
độ
gốc
là
.
Vậy,
tung
độ
gốc
là
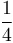 .
.
-
Trong
bài
toán
ví
dụ,
phương
trình
trở
thành:
-
Kiểm
tra
tính
toán.
Trên
độ
thị
tọa
độ,
biểu
diễn
điểm
đã
biết
rồi
dựa
vào
hệ
số
góc,
vẽ
đường
thẳng
đi
qua
điểm
đó.
Để
tìm
tung
độ
góc,
tìm
điểm
mà
tại
đó,
đường
thẳng
này
đi
qua
trục
tung.
-
Ví
dụ,
nếu
hệ
số
góc
là
 và
điểm
cho
trước
là
(5,4),
lấy
một
điểm
ở
tọa
độ
(5,4)
và
vẽ
những
điểm
khác
dọc
đường
bằng
cách
đếm
sang
trái
3
và
xuống
4.
Khi
vẽ
một
đường
đi
qua
các
điểm,
đường
vẽ
thu
được
nên
cắt
trục
tung
ở
điểm
nằm
trên
gốc
tọa
độ
(0,0).
và
điểm
cho
trước
là
(5,4),
lấy
một
điểm
ở
tọa
độ
(5,4)
và
vẽ
những
điểm
khác
dọc
đường
bằng
cách
đếm
sang
trái
3
và
xuống
4.
Khi
vẽ
một
đường
đi
qua
các
điểm,
đường
vẽ
thu
được
nên
cắt
trục
tung
ở
điểm
nằm
trên
gốc
tọa
độ
(0,0).
-
Ví
dụ,
nếu
hệ
số
góc
là
Tìm hoành độ gốc khi biết hệ số góc và tung độ gốc[sửa]
-
Thiết
lập
công
thức
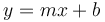 .
Trong
đó:
y
=
tung
độ
của
điểm
bất
kỳ
trên
đường
thẳng,
m
=
hệ
số
góc,
x
=
hoành
độ
của
điểm
bất
kỳ
trên
đường
thẳng
và
b
=
tung
độ
gốc.
.
Trong
đó:
y
=
tung
độ
của
điểm
bất
kỳ
trên
đường
thẳng,
m
=
hệ
số
góc,
x
=
hoành
độ
của
điểm
bất
kỳ
trên
đường
thẳng
và
b
=
tung
độ
gốc.
-
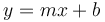 là
phương
trình
đường
thẳng.[6]
là
phương
trình
đường
thẳng.[6] - Hoành độ gốc là điểm mà tại đó, đường thẳng đi qua trục hoành.
-
-
Thế
hệ
số
góc
và
tung
độ
gốc
vào
công
thức.
Nhớ
rằng,
hệ
số
góc
bằng
thay
đổi
dọc
trên
thay
đổi
ngang.
Nếu
cần
hỗ
trợ
trong
việc
tìm
hệ
số
góc,
bạn
có
thể
tham
khảo
hướng
dẫn
ở
trên.
-
Ví
dụ,
nếu
hệ
số
góc
là
 và
tung
độ
gốc
là
và
tung
độ
gốc
là
 ,
công
thức
thu
được
sẽ
là:
,
công
thức
thu
được
sẽ
là:
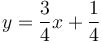 .
.
-
Ví
dụ,
nếu
hệ
số
góc
là
-
Cho
y
bằng
0.[7]
Bạn
đang
tìm
hoành
độ
gốc,
điểm
mà
tại
đó,
đường
thẳng
cắt
với
trục
hoành.
Tại
điểm
này,
tung
độ
sẽ
bằng
0.
Vậy
nên,
nếu
cho
y
bằng
0
và
giải
phương
trình
thu
được
để
tìm
hoành
độ
tương
ứng,
ta
thu
được
điểm
(x,
0)
-
chính
là
hoành
độ
gốc
cần
tìm.
-
Ở
bài
toán
ví
dụ,
phương
trình
trở
thành:
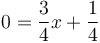 .
.
-
Ở
bài
toán
ví
dụ,
phương
trình
trở
thành:
-
Hoàn
thành
và
giải
phương
trình,
tìm
x.
Đầu
tiên,
trừ
hai
vế
cho
tung
độ
gốc.
Tiếp
đến,
chia
cả
hai
vế
cho
hệ
số
góc.
-
Ở
bài
toán
ví
dụ,
phương
trình
trở
thành:
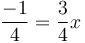 .
Chia
cả
hai
vế
cho
.
Chia
cả
hai
vế
cho
 ,
thu
được:
,
thu
được:
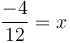 .
Rút
gọn
ta
có:
.
Rút
gọn
ta
có:
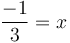 .
Vậy
điểm
mà
tại
đó,
đường
thẳng
đi
qua
trục
hoành
là
.
Vậy
điểm
mà
tại
đó,
đường
thẳng
đi
qua
trục
hoành
là
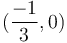 .
Vậy
hoành
độ
gốc
là
.
Vậy
hoành
độ
gốc
là
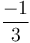 .
.
-
Ở
bài
toán
ví
dụ,
phương
trình
trở
thành:
-
Kiểm
tra
tính
toán.
Trên
đồ
thị
tọa
độ,
biểu
diễn
tung
độ
gốc
của
bạn,
tiếp
đến,
dựa
vào
hệ
số
góc,
vẽ
đường
thẳng.
Để
tìm
hoành
độ
gốc,
tìm
điểm
mà
tại
đó,
đường
thẳng
cắt
trục
hoành.
-
Ví
dụ,
nếu
hệ
số
góc
là
 và
tung
độ
gốc
là
và
tung
độ
gốc
là
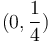 ,
biểu
diễn
điểm
,
biểu
diễn
điểm
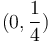 và
vẽ
những
điểm
khác
dọc
theo
đường
thẳng
bằng
cách
đếm
sang
trái
3
và
xuống
4
rồi
sang
phải
3
và
lên
4.
Khi
vẽ
một
đường
đi
qua
các
điểm,
đường
thẳng
thu
được
nên
cắt
trục
hoành
chỉ
bên
trái
đôi
chút
so
với
gốc
tọa
độ
(0,0).
và
vẽ
những
điểm
khác
dọc
theo
đường
thẳng
bằng
cách
đếm
sang
trái
3
và
xuống
4
rồi
sang
phải
3
và
lên
4.
Khi
vẽ
một
đường
đi
qua
các
điểm,
đường
thẳng
thu
được
nên
cắt
trục
hoành
chỉ
bên
trái
đôi
chút
so
với
gốc
tọa
độ
(0,0).
-
Ví
dụ,
nếu
hệ
số
góc
là
- Hình cuối:
Nguồn và Trích dẫn[sửa]
- ↑ 1,0 1,1 http://www.mathopenref.com/coordslope.html
- ↑ http://www.columbia.edu/itc/sipa/math/slope_linear.html
- ↑ http://serc.carleton.edu/mathyouneed/slope/slopes.html
- ↑ 4,0 4,1 http://www.coolmath.com/algebra/08-lines/05-finding-slope-line-from-graph-01
- ↑ http://www.coolmath.com/algebra/08-lines/06-finding-slope-line-given-two-points-01
- ↑ 6,0 6,1 http://www.mathopenref.com/coordequation.html
- ↑ https://www.youtube.com/watch?v=wPs0tjl8Vpg
- Sổ làm việc được dùng cho bài viết này là "y = ax + b.xlsx"


